RTG A Recursive Realistic Graph Generator using Random

RTG: A Recursive Realistic Graph Generator using Random Typing Leman Akoglu and Christos Faloutsos Carnegie Mellon University

Outline • • Motivation Problem Definition Related Work A Little History Proposed Model Experimental Results Conclusion 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 2

Motivation - 1 Complex graphs --WWW, computer, biological, social networks, etc. exhibit many common properties: - power laws - small and shrinking diameter - community structure -… How can we produce synthetic but realistic graphs? http: //www. aharef. info/static/htmlgraph/ 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 3

Motivation - 2 Why do we need synthetic graphs? • • Simulation Sampling/Extrapolation Summarization/Compression Motivation to understand pattern generating processes 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 4

Problem Definition Discover a graph generator that is: G 1. simple: the more intuitive the better! G 2. realistic: outputs graphs that obey all “laws” G 3. parsimonious: requires few parameters G 4. flexible: able to produce the cross-product of un/weighted, un/directed, uni/bipartite graphs G 5. fast: generation should take linear time with the size of the output graph 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 5

Outline • • Motivation Problem Definition Related Work A Little History Proposed Model Experimental Results Conclusion 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 6

Related Work 1. Graph Properties What we want to match 2. Graph Generators What has been proposed earlier 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 7

Related Work 1: Graph Properties 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 8

Related Work 2: Graph Generators • • • Erdős-Rényi (ER) model [Erdős, Rényi `60] Small-world model [Watts, Strogatz `98] Preferential Attachment [Barabási, Albert `99] Winners don’t take all [Pennock et al. `02] Forest Fire model [Leskovec, Faloutsos `05] Butterfly model [Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 9

Related Work 2: Graph Generators • • • Erdős-Rényi (ER) model [Erdős, Rényi `60] Small-world model [Watts, Strogatz `98] • Model some static graph property Preferential Attachment [Barabási, Albert `99] • Neglect dynamic properties Winners don’t take all [Pennock et al. `02] • Cannot produce weighted graphs. Forest Fire model [Leskovec, Faloutsos `05] Butterfly model [Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 10

Related Work 2: Graph Generators • Random dot-product graphs [Kraetzl, Nickel `05] [Young, Scheinerman `07] • Utility-based models [Fabrikant et al. ’ 02] [Even-Bar et al. `07] [Laoutaris, `08] • Kronecker graphs [Leskovec et al. `07] [Akoglu et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 11

Related Work 2: Graph Generators • Produces only undirected graphs • Random dot-product graphs • [Kraetzl, Cannot. Nickel produce weighted graphs. `05] [Young, Scheinerman `07] • Requires quadratic time • Utility-based models [Fabrikant et al. ’ 02] [Even-Bar et al. `07] [Laoutaris, `08] • Kronecker graphs [Leskovec et al. `07] [Akoglu et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 12

Related Work 2: Graph Generators • Produces only undirected graphs • Random dot-product graphs • [Kraetzl, Cannot. Nickel produce weighted graphs. `05] [Young, Scheinerman `07] • Requires quadratic time • Utility-based models [Fabrikant et al. ’ 02] • Hardettoal. analyze [Even-Bar `07] [Laoutaris, `08] • Kronecker graphs [Leskovec et al. `07] [Akoglu et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 13

Related Work 2: Graph Generators • Produces only undirected graphs • Random dot-product graphs • [Kraetzl, Cannot. Nickel produce weighted graphs. `05] [Young, Scheinerman `07] • Requires quadratic time • Utility-based models [Fabrikant et al. ’ 02] • Hardettoal. analyze [Even-Bar `07] [Laoutaris, `08] • Multinomial/Lognormal distrib. • Kronecker graphs • [Leskovec Fixed number nodes `08] et al. `07]of[Akoglu, 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 14

Outline • • Motivation Problem Definition Related Work A Little History Proposed Model Experimental Results Conclusion 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 15

A Little History - 1 [Zipf, 1932] count In many natural languages, the rank r and the frequency fr of words follow a power law: fr ∝ 1/r 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 rank 16

A Little History - 2 [Mandelbrot, 1953] “Humans optimize avg. information per unit transmission cost. ” 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 17

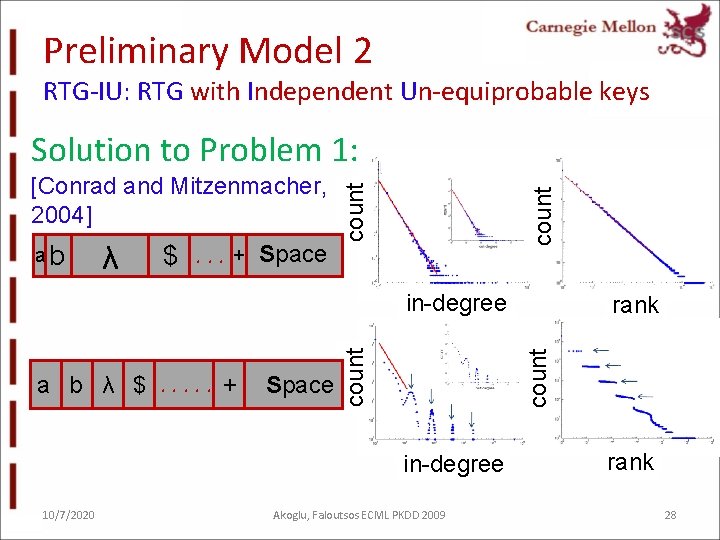
A Little History - 2 [Miller, 1957] “A monkey types randomly on a keyboard: a b λ $. . . + Space k equiprobable keys Distribution of words follow a power- law. ” 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 18

A Little History - 2 [Conrad and Mitzenmacher, 2004] “Same relation still holds when keys have unequal probabilities. ” ab 10/7/2020 λ $. . . + Akoglu, Faloutsos ECML PKDD 2009 Space 19

Outline • • Motivation Problem Definition Related Work A Little History Proposed Model Experimental Results Conclusion 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 20

Preliminary Model 1 RTG-IE: RTG with Independent Equiprobable keys Space 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 21

Preliminary Model 1 RTG-IE: RTG with Independent Equiprobable keys Lemma 1. W is super-linear on N (power law): Lemma 2. W is super-linear on E (power law): Lemma 3. In(out)-weight Wn of node n is super-linear on in(out)-degree dn (power law): , where Please find the proofs in the paper. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 22

Graph Properties 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 23

Preliminary Model 1 RTG-IE: RTG with Independent Equiprobable keys L 05. Densificationon. PLN (power law): Lemma 1. W is super-linear L 11. Weight PL on E (power law): Lemma 2. W is super-linear Lemma 3. In(out)-weight Wn of node n is super-linear on L 10. Snapshot PL in(out)-degree dn (power law): , where Please find the proofs in the paper. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 24

Advantages of the Preliminary Model 1 G 1 - Intuitive G 1 - Easy to implement G 2 - Realistic –provably follows several rules G 3 - Handful of parameters –k, q, W G 5 - Fast –generating random sequence of char. s 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 25

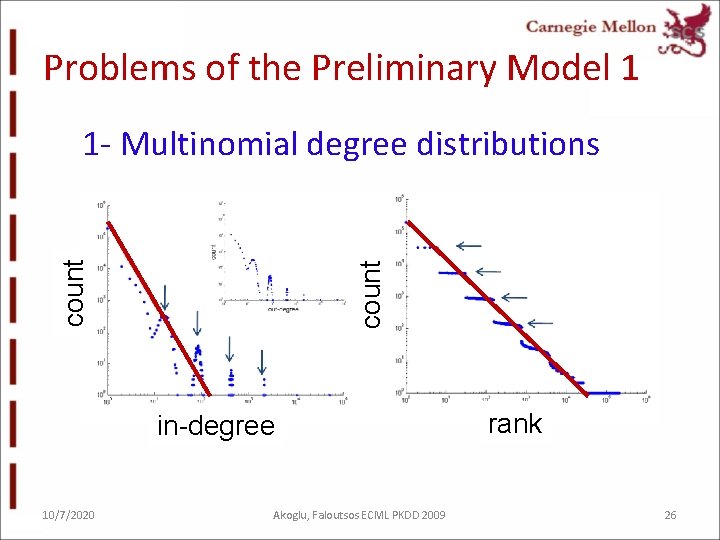
Problems of the Preliminary Model 1 count 1 - Multinomial degree distributions in-degree 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 rank 26

Problems of the Preliminary Model 1 2 - No homophily, no community structure Node i connects to any node j with prob. di*dj independently, rather than connecting to ‘similar’ nodes. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 27

Preliminary Model 2 RTG-IU: RTG with Independent Un-equiprobable keys ab λ $. . . + Space count [Conrad and Mitzenmacher, 2004] count Solution to Problem 1: Space in-degree 10/7/2020 rank count a b λ $. . . + count in-degree Akoglu, Faloutsos ECML PKDD 2009 rank 28

Proposed Model RTG: Random Typing Graphs Solution to Problem 2: “ 2 D keyboard” • Generate sourcedestination labels in one shot. • Pick one of the nine keys randomly. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 29

Proposed Model RTG: Random Typing Graphs Solution to Problem 2: “ 2 D keyboard” • Repeat recursively. • Terminate each label when the space key is typed on each dimension (dark blue). 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 30

Proposed Model RTG: Random Typing Graphs 10/7/2020 pa*pa pa*pb pa*q pb*pa pb*pb pb*q q*pa q*pb q*q Solution to Problem 2: “ 2 D keyboard” How do we choose the keys? Independent model does not yield community structure! Akoglu, Faloutsos ECML PKDD 2009 31

Proposed Model RTG: Random Typing Graphs Solution to Problem 2: “ 2 D keyboard” • Boost probability of diagonal keys and decrease probability of off-diagonal ones (0<β<1: imbalance factor) 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 32

Proposed Model RTG: Random Typing Graphs Solution to Problem 2: “ 2 D keyboard” • Boost probability of diagonal keys and decrease probability of off-diagonal ones (0<β<1: imbalance factor) • Favoring of diagonal keys creates homophily. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 33

Proposed Model Parameters • k: Number of keys • q: Probability of hitting the space key S • W: Number of multiedges in output graph G • β: imbalance factor 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 34

Proposed Model Up to this point, we discussed directed, weighted and unipartite graphs. Generalizations - Undirected graphs: Ignore edge directions; edge generation is symmetric. - Unweighted graphs: Ignore duplicate edges. - Bipartite graphs: Different key sets on source and destination; labels are different. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 35

Outline • • Motivation Problem Definition Related Work A Little History Proposed Model Experimental Results Conclusion 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 36

Experimental Results How does RTG model real graphs? • Blognet: a social network of blogs based on citations undirected, unweighted and unipartite N = 27, 726; E = 126, 227; over 80 time ticks. • Com 2 Cand: the U. S. electoral campaign donations network from organizations to candidates directed, weighted ($ amounts) and bipartite N = 23, 191; E = 877, 721; W = 4, 383, 105, 580 over 29 time ticks. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 37

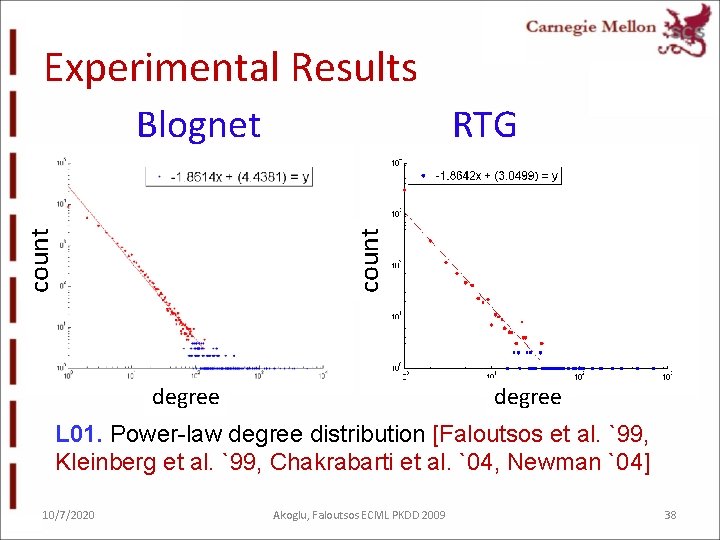
Experimental Results RTG count Blognet degree L 01. Power-law degree distribution [Faloutsos et al. `99, Kleinberg et al. `99, Chakrabarti et al. `04, Newman `04] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 38

Experimental Results RTG count Blognet triangles L 02. Triangle Power Law (TPL) [Tsourakakis `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 39

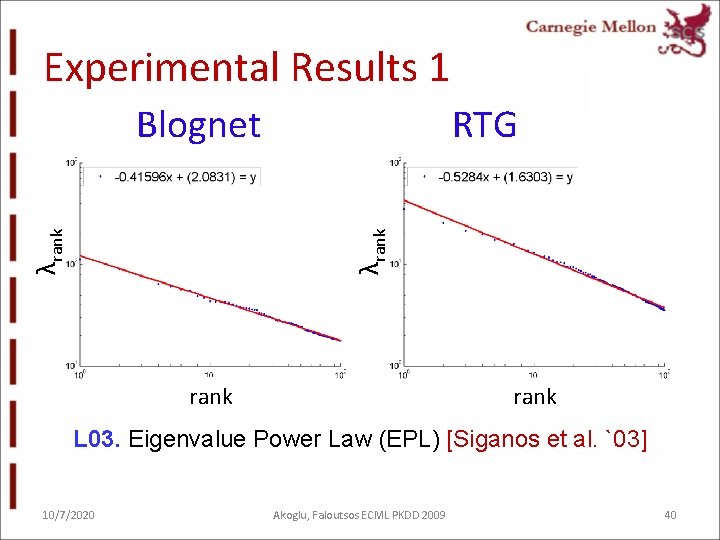
Experimental Results 1 RTG λrank Blognet rank L 03. Eigenvalue Power Law (EPL) [Siganos et al. `03] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 40

Graph Properties 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 41

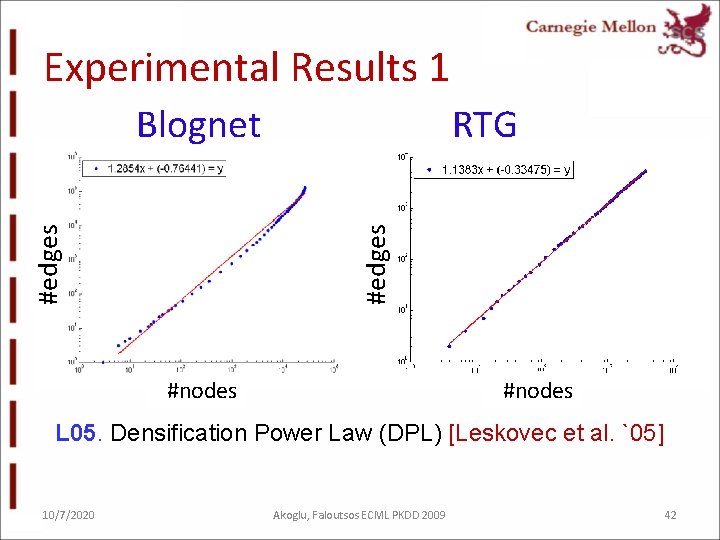
Experimental Results 1 RTG #edges Blognet #nodes L 05. Densification Power Law (DPL) [Leskovec et al. `05] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 42

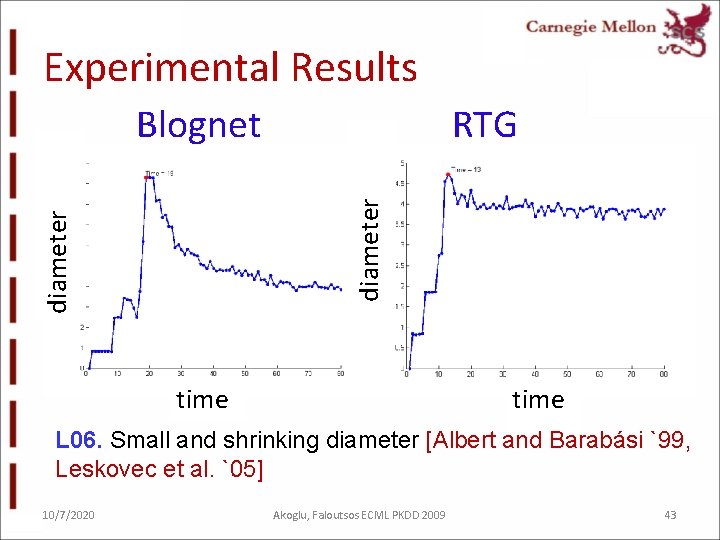
Experimental Results RTG diameter Blognet time L 06. Small and shrinking diameter [Albert and Barabási `99, Leskovec et al. `05] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 43

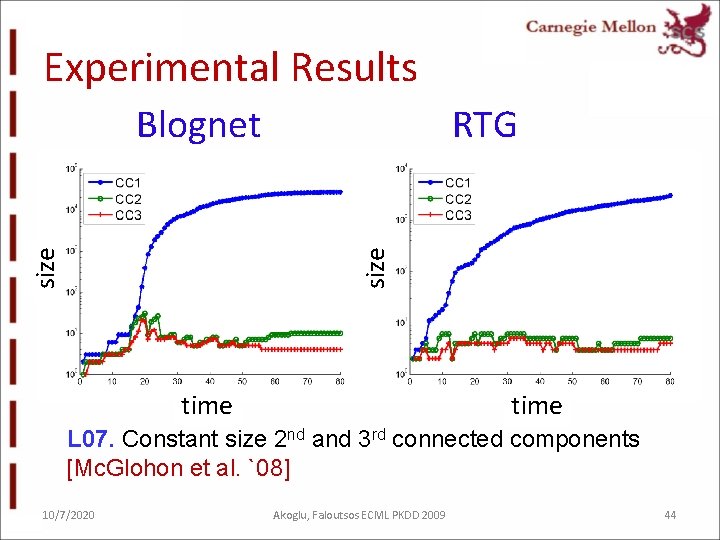
Experimental Results RTG size Blognet time L 07. Constant size 2 nd and 3 rd connected components [Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 44

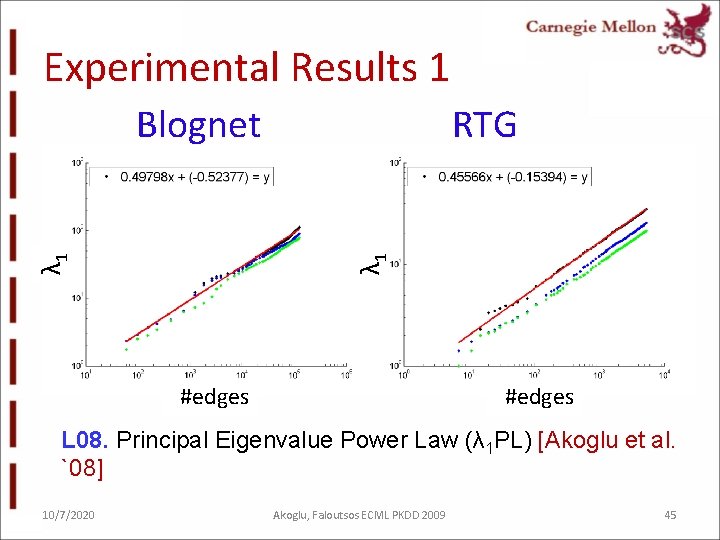
Experimental Results 1 RTG λ 1 Blognet #edges L 08. Principal Eigenvalue Power Law (λ 1 PL) [Akoglu et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 45

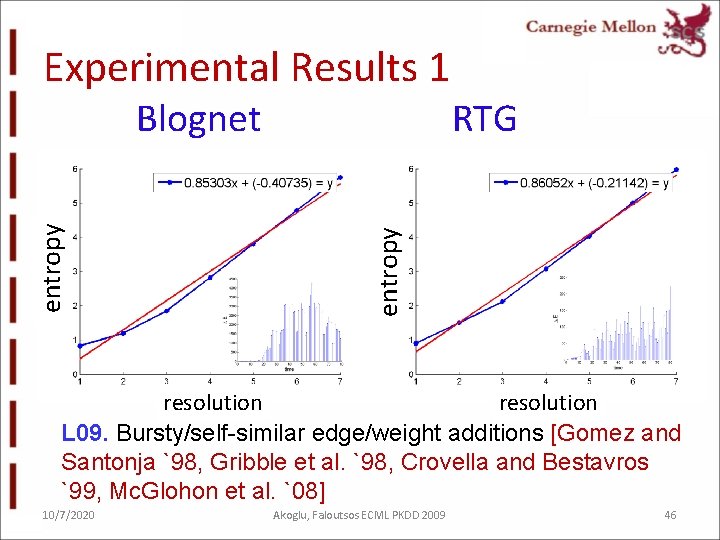
Experimental Results 1 RTG entropy Blognet resolution L 09. Bursty/self-similar edge/weight additions [Gomez and Santonja `98, Gribble et al. `98, Crovella and Bestavros `99, Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 46

Graph Properties 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 47

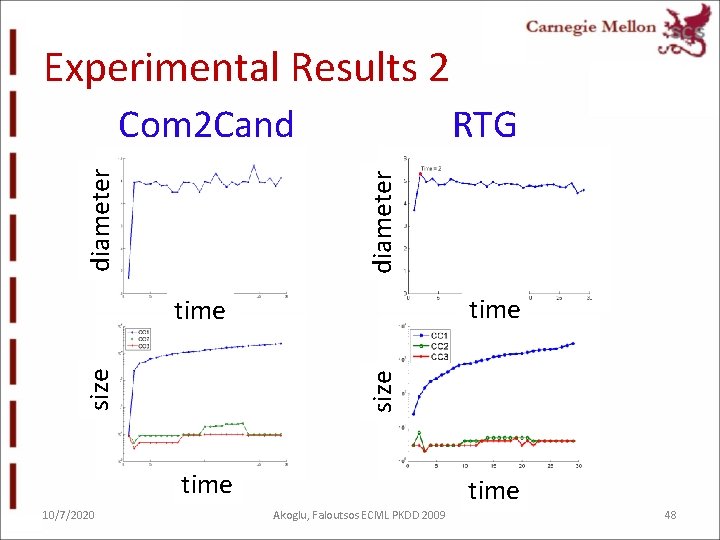
Experimental Results 2 RTG diameter Com 2 Cand time size time 10/7/2020 time Akoglu, Faloutsos ECML PKDD 2009 48

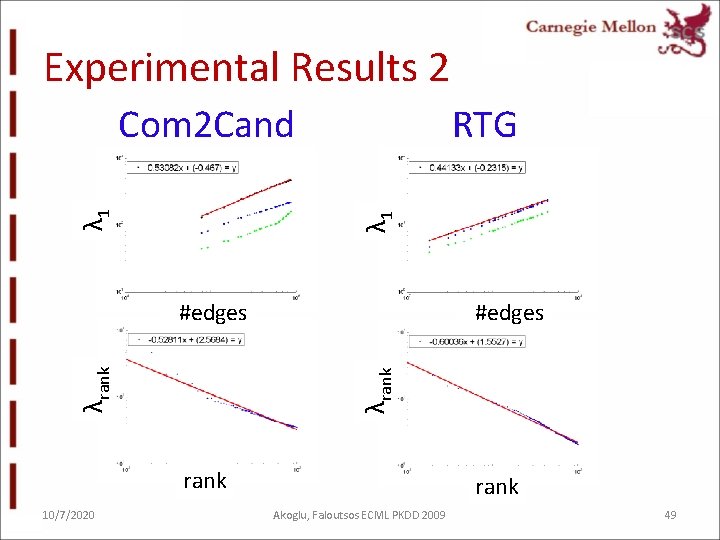
Experimental Results 2 RTG λ 1 Com 2 Cand #edges λrank #edges rank 10/7/2020 rank Akoglu, Faloutsos ECML PKDD 2009 49

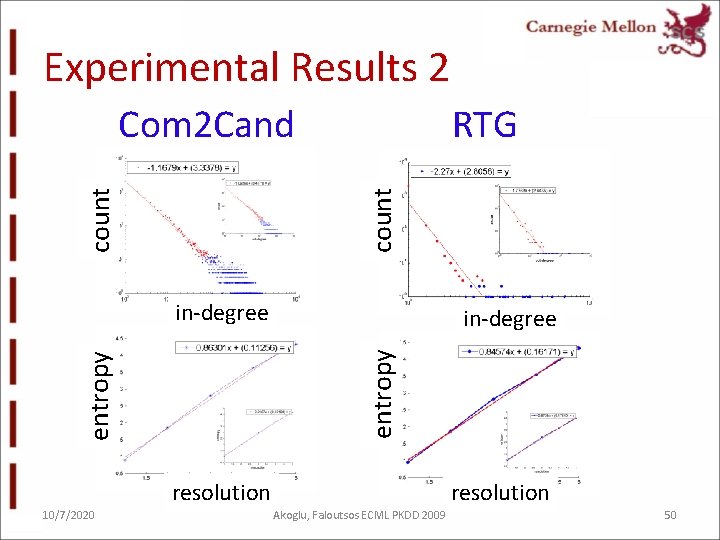
Experimental Results 2 RTG count Com 2 Cand in-degree entropy in-degree resolution 10/7/2020 resolution Akoglu, Faloutsos ECML PKDD 2009 50

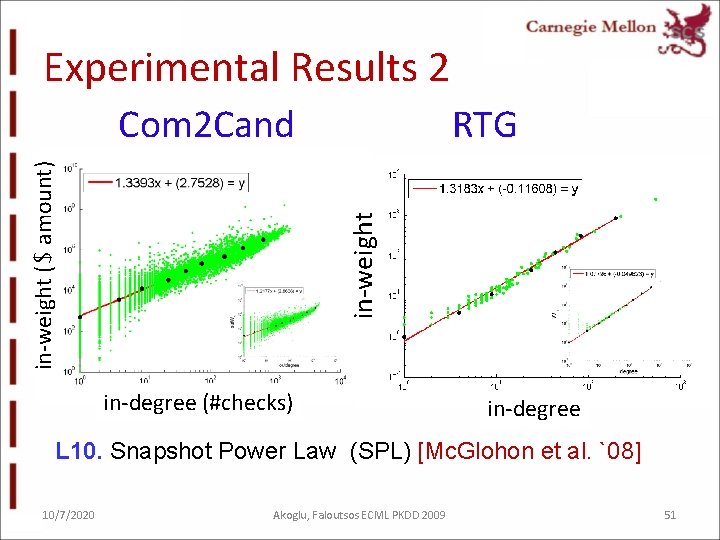
Experimental Results 2 RTG in-weight ($ amount) Com 2 Cand in-degree (#checks) in-degree L 10. Snapshot Power Law (SPL) [Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 51

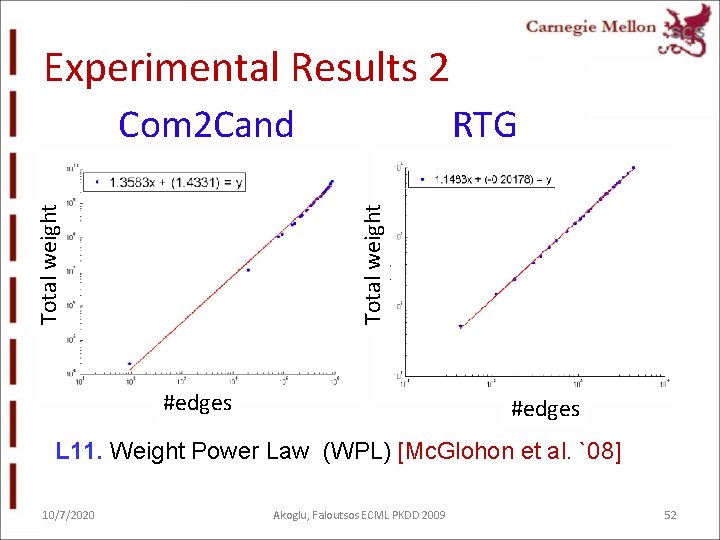
Experimental Results 2 RTG Total weight Com 2 Cand #edges L 11. Weight Power Law (WPL) [Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 52

Graph Properties 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 53

Experimental Results more community structure On “modularity” [Girvan and Newman `02] “Modularity “ decreases with increasing β No significant modularity --RTG-IE 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 54

Graph Properties 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 55

Experimental Results time (ms) On complexity Computation time grows linearly with increasing W 2 M multi-edges in 7 sec. s #multi-edges 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 56

Outline • • Motivation Problem Definition Related Work A Little History Proposed Model Experimental Results Conclusion 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 57

Conclusion 1 Our model is: G 1. simple and intuitive --few lines of code G 2. realistic --graphs that obey all eleven properties in real graphs G 3. parsimonious --only a handful of parameters G 4. flexible --can generate weighted/unweighted, directed/undirected, unipartite/bipartite graphs and any combination of those G 5. fast --linear on the size of the output graph 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 58

Conclusion 2 We showed that: 10/7/2020 RTG mimics real graphs well. Akoglu, Faloutsos ECML PKDD 2009 59

Contact Leman Akoglu www. cs. cmu. edu/~lakoglu@cs. cmu. edu Christos Faloutsos www. cs. cmu. edu/~christos@cs. cmu. edu 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 60

A Little History - 3 The infinite monkey theorem: A monkey typing randomly on a keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 61

Proposed Model Burstiness and Self-similarity If each step is a time tick, weight additions are uniform! • Start with a uniform interval • Recursively subdivide weight additions to each half, Total Weight quarter, and so on, according to the bias b > 0. 5 • b -fraction of the additions happen in one “half” and Time the remaining in the other. 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 62

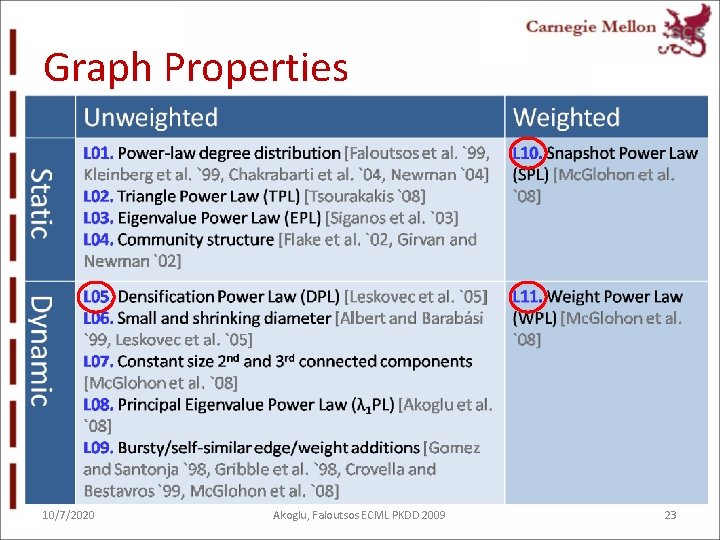
Related Work: Graph Properties Static Unweighted Weighted L 01. Power-law degree distribution [Faloutsos et al. `99, Kleinberg et al. `99, Chakrabarti et al. `04, Newman `04] L 02. Triangle Power Law (TPL) [Tsourakakis `08] L 03. Eigenvalue Power Law (EPL) [Siganos et al. `03] L 04. Community structure [Flake et al. `02, Girvan and Newman `02] L 10. Snapshot Power Law (SPL) [Mc. Glohon et al. `08] Dynamic L 05. Densification Power Law (DPL) [Leskovec et al. `05] L 11. Weight Power Law L 06. Small and shrinking diameter [Albert and Barabási (WPL) [Mc. Glohon et al. `99, Leskovec et al. `05] `08] L 07. Constant size 2 nd and 3 rd connected components [Mc. Glohon et al. `08] L 08. Principal Eigenvalue Power Law (λ 1 PL) [Akoglu et al. `08] L 09. Bursty/self-similar edge/weight additions [Gomez and Santonja `98, Gribble et al. `98, Crovella and Bestavros `99, Mc. Glohon et al. `08] 10/7/2020 Akoglu, Faloutsos ECML PKDD 2009 63