Rsolution dune quation quation Une quation est un

Équation • Une équation est un énoncé qui indique l’égalité entre 2 expressions. •

Équation • Pour rendre une équation vraie, on trouve la solution ou la racine.

Équation Pour trouver la solution, tu dois isoler x pour trouver la solution.

Types d’équations explorés • Équation du premier degré – Une variable avec exposant de

Les étapes: D. E. N. I. Q. Résoudre pour x:

Les étapes: D. E. N. I. Q. Résoudre pour x: • Distributivité: débarrasses-toi des

Devoirs: p. 179 nos 1 à 38 (pairs) et 39 à 43 au complet.

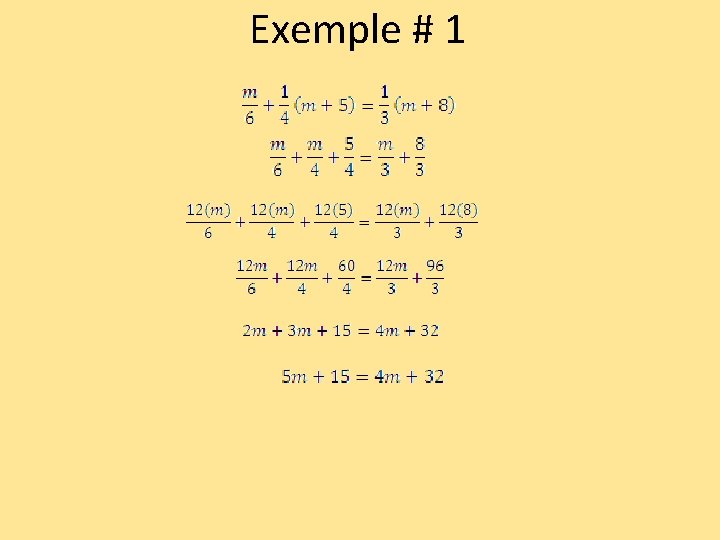
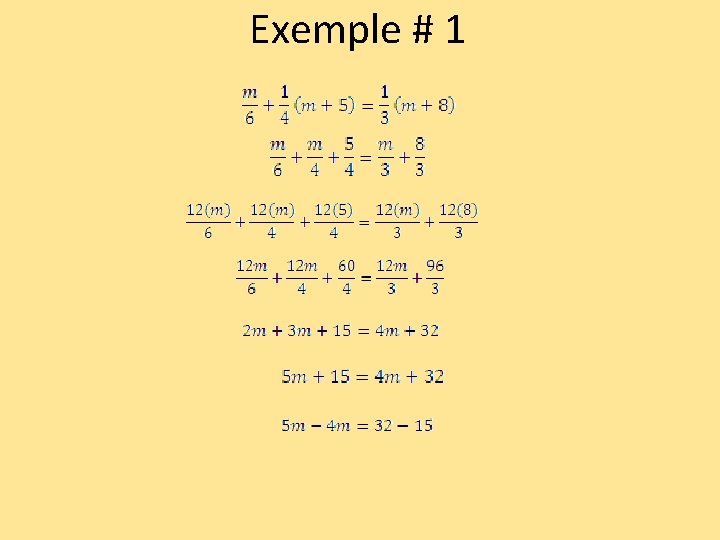
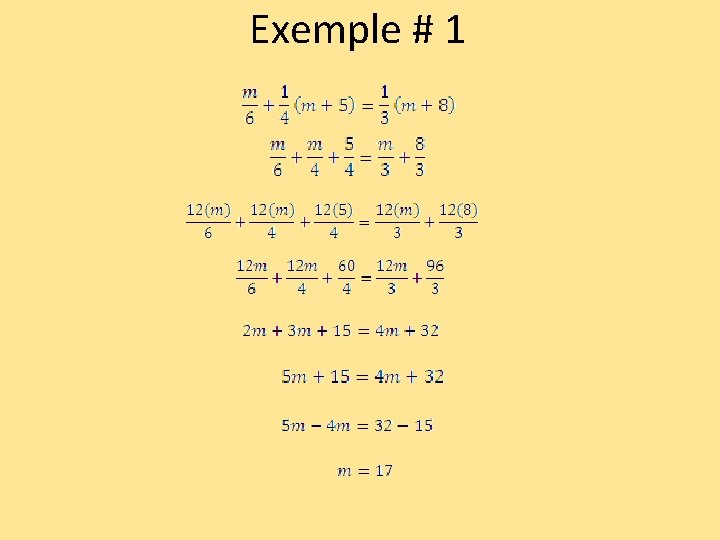
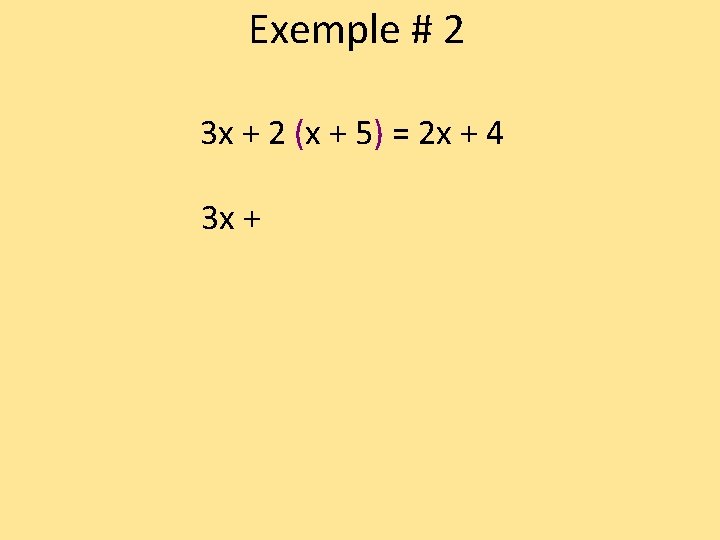
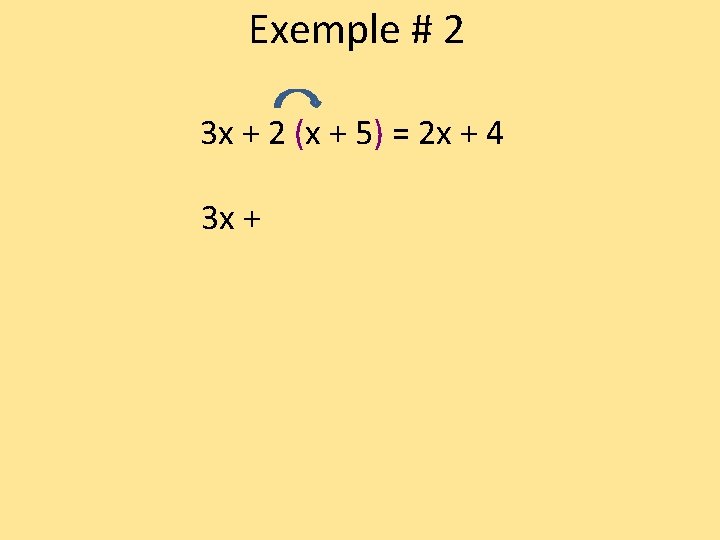
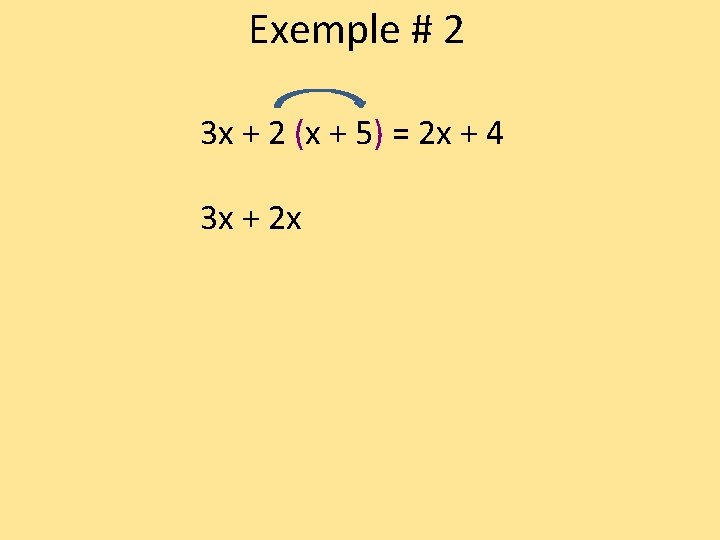
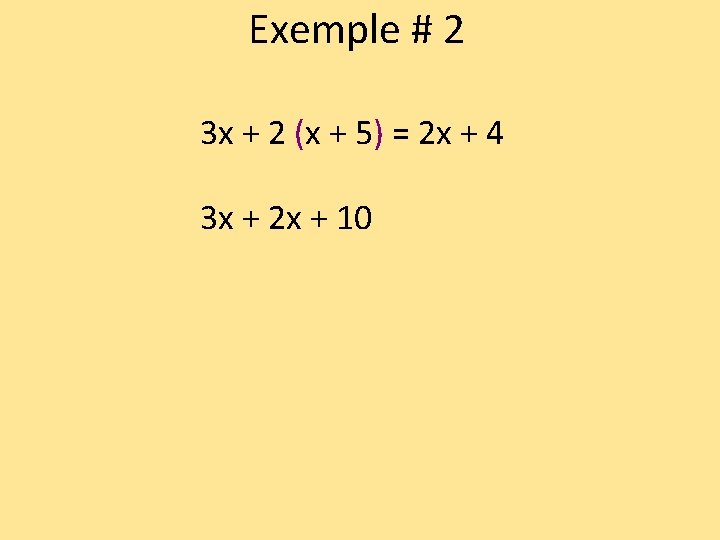
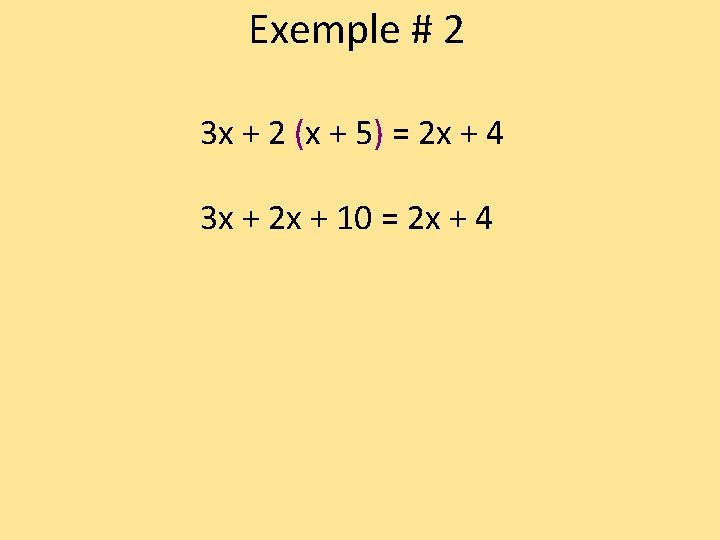
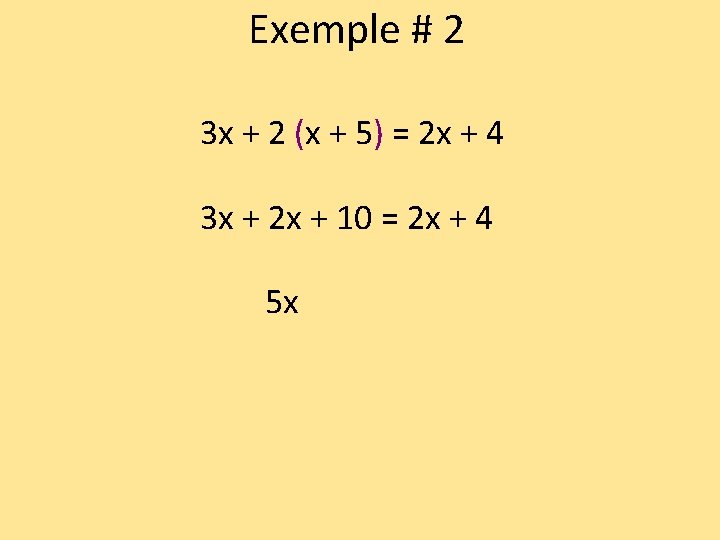
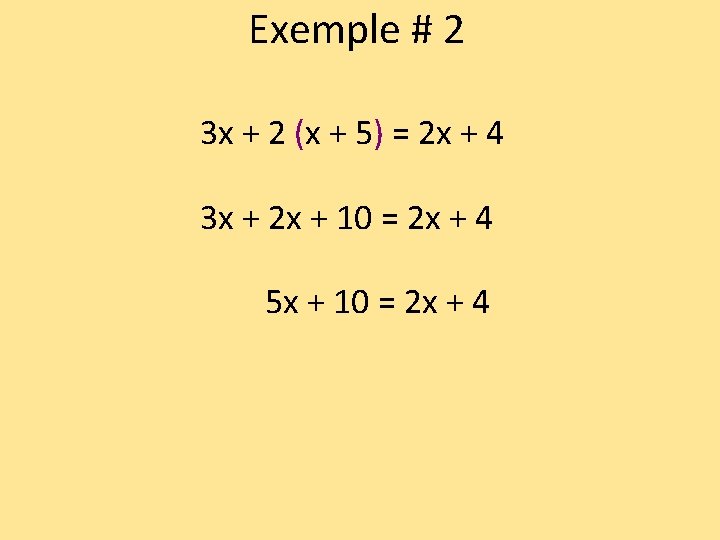
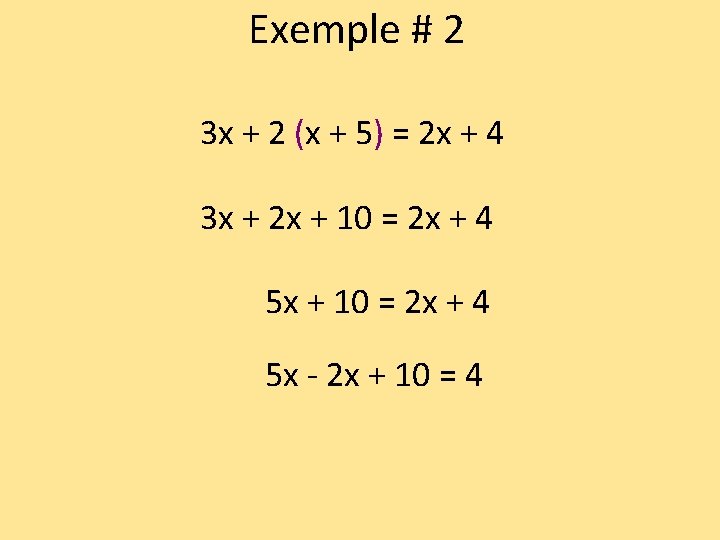
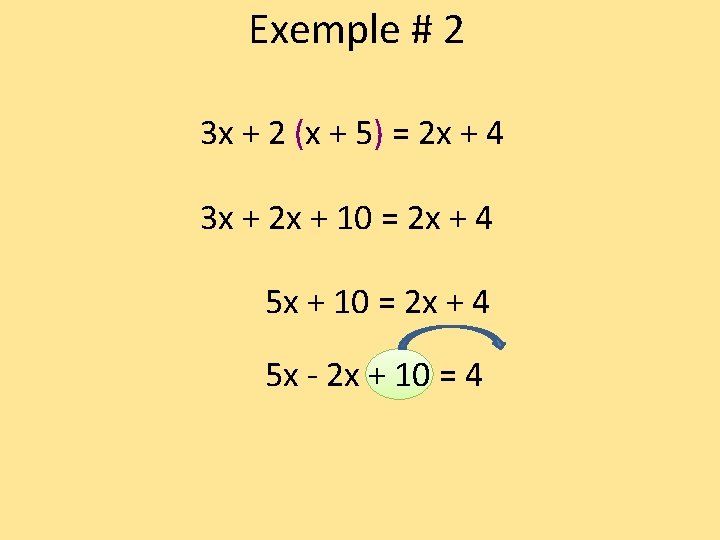
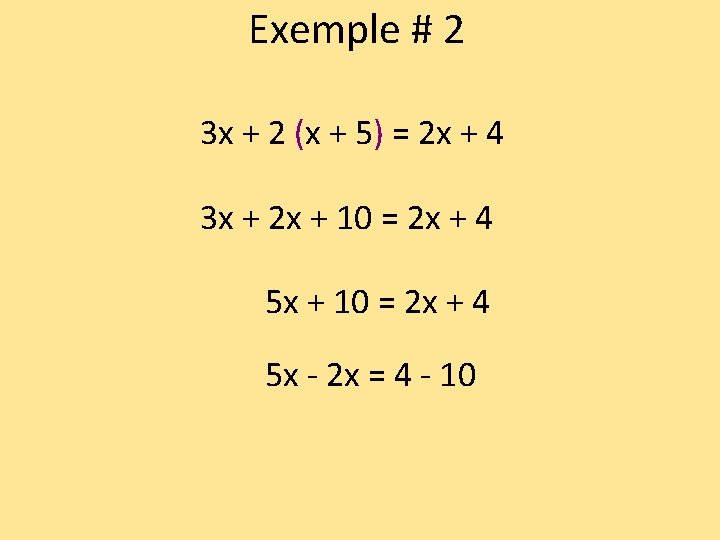
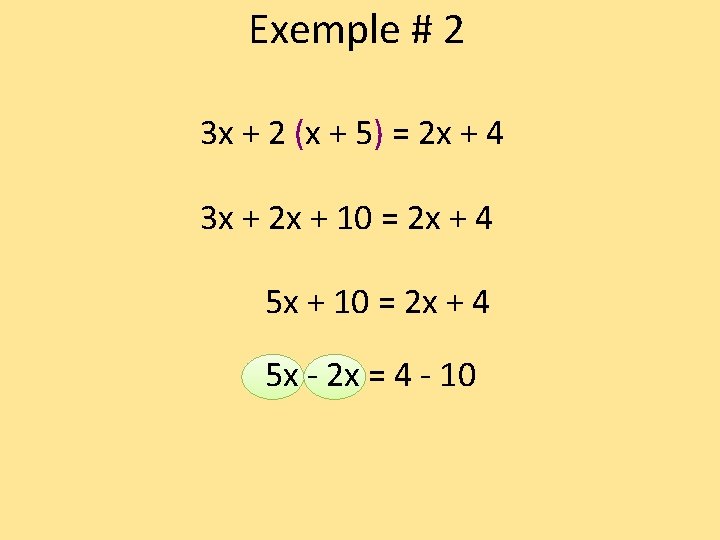
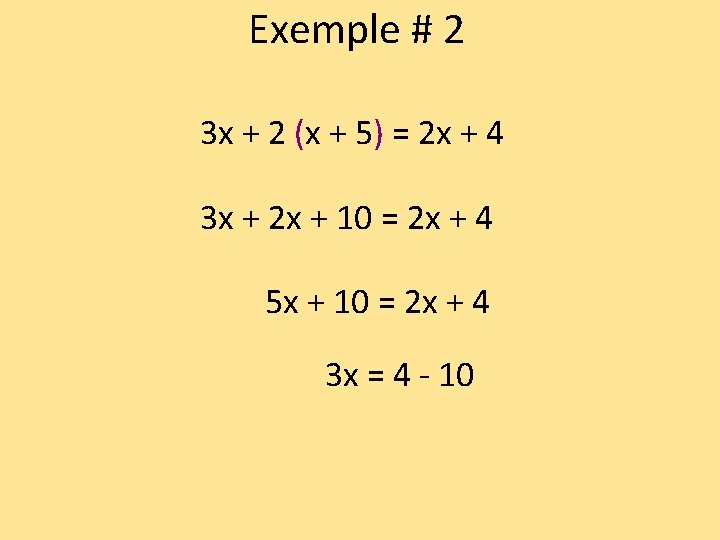
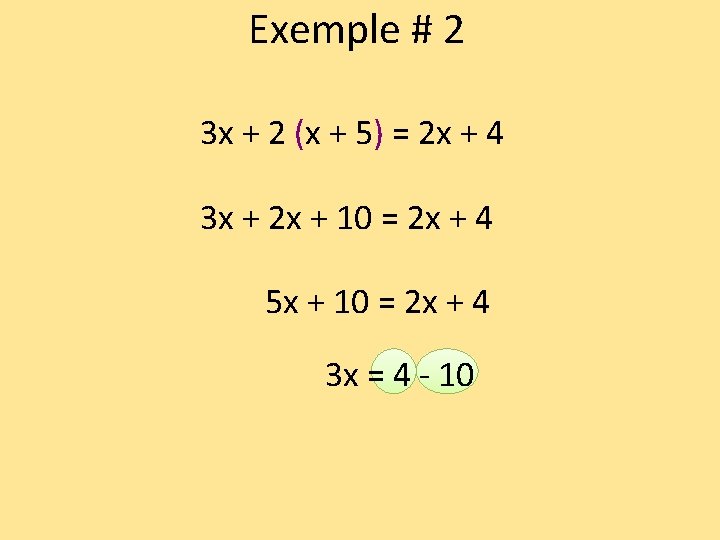
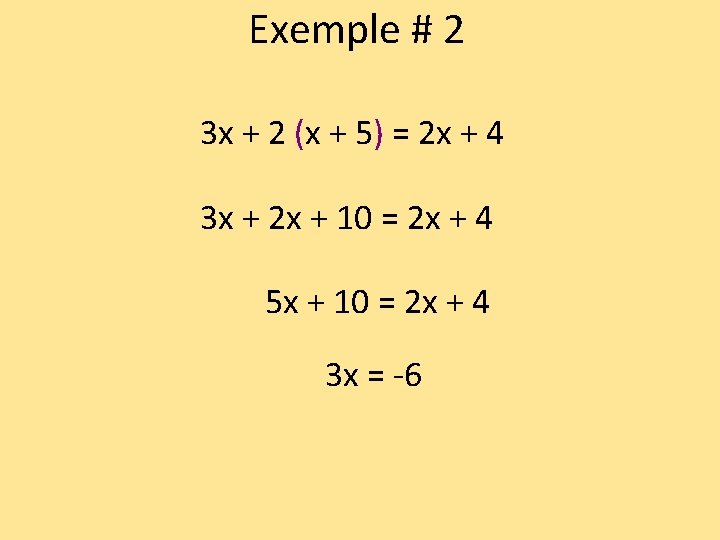
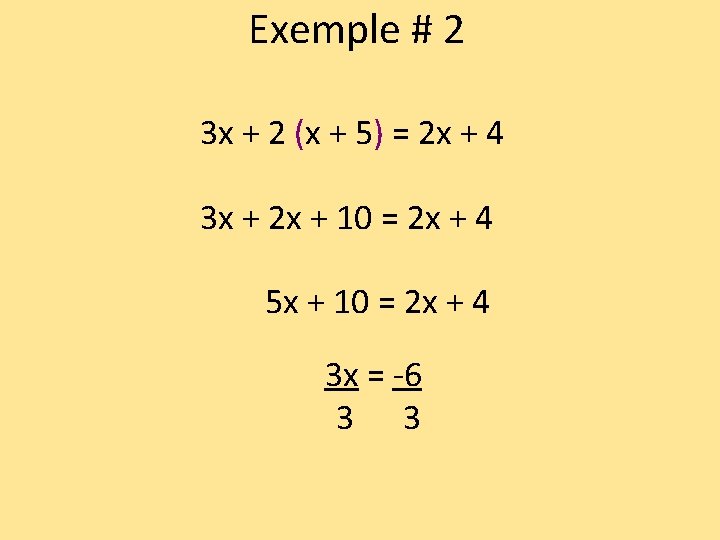
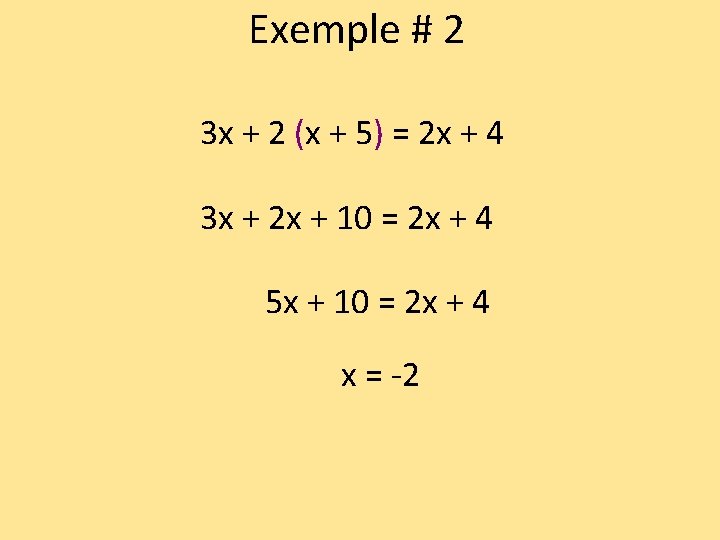
Slides: 41

Download presentation

Résolution d’une équation

Équation • Une équation est un énoncé qui indique l’égalité entre 2 expressions. • L’équation 2 x + 3 = 5 est dite proposition ouverte parce qu’elle peut être vraie ou fausse.

Équation • Pour rendre une équation vraie, on trouve la solution ou la racine. • 2 x + 3 = 5 est vraie seulement si x =1.

Équation Pour trouver la solution, tu dois isoler x pour trouver la solution.

Types d’équations explorés • Équation du premier degré – Une variable avec exposant de 1 Exemples au tableau : 1) 3 x – 6 = x + 4 2) 4(3 a + 6) + 2 = 3 a – 10 • Équation rationnelle – Équation contenant des fractions

Les étapes: D. E. N. I. Q. Résoudre pour x:

Les étapes: D. E. N. I. Q. Résoudre pour x: • Distributivité: débarrasses-toi des parenthèses en distribuant

Les étapes: D. E. N. I. Q. Résoudre pour x: • Distributivité: débarrasses-toi des parenthèses en distribuant • Élimination: débarrasses-toi des fractions en utilisant un facteur commun

Les étapes: D. E. N. I. Q. Résoudre pour x: • Distributivité: débarrasses-toi des parenthèses en distribuant • Élimination: débarrasses-toi des fractions en utilisant un facteur commun • Nettoyage: nettoie chaque côté en simplifiant • Isolement: isole le terme - x en apportant tout les termes contenant x sur le côté gauche.

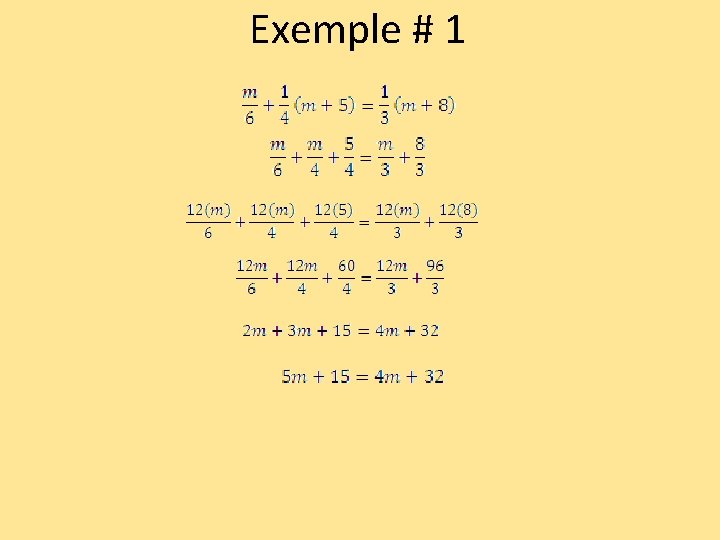
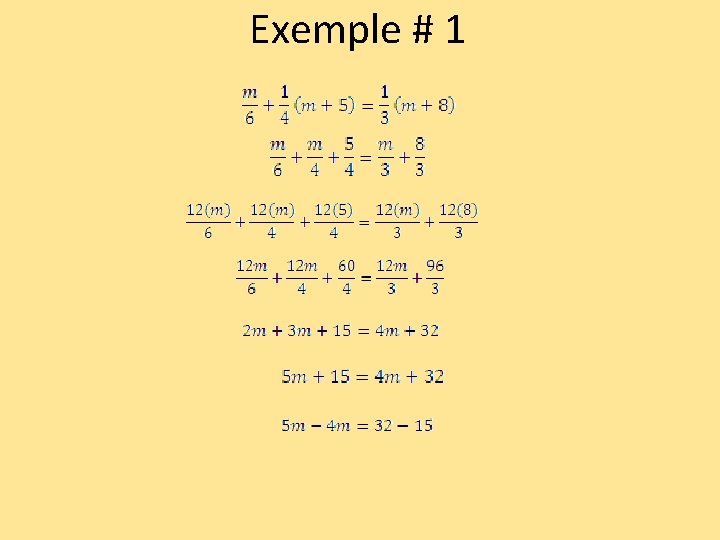
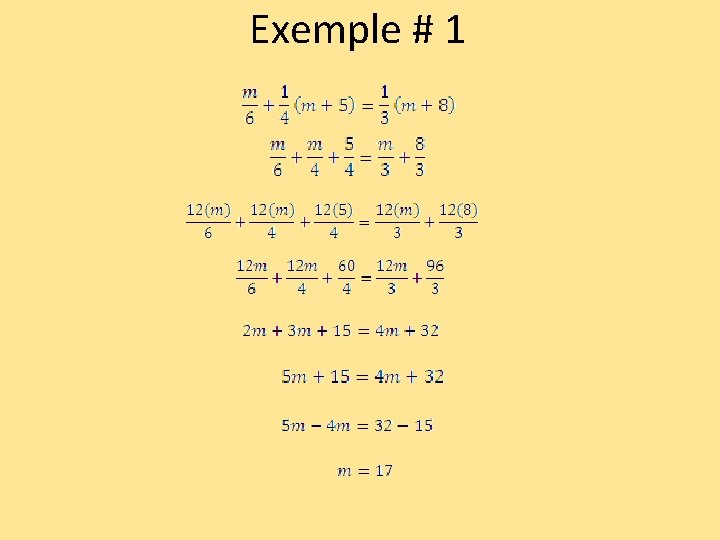
Exemple # 1

Exemple # 2 3 x + 2 (x + 5) = 2 x + 4

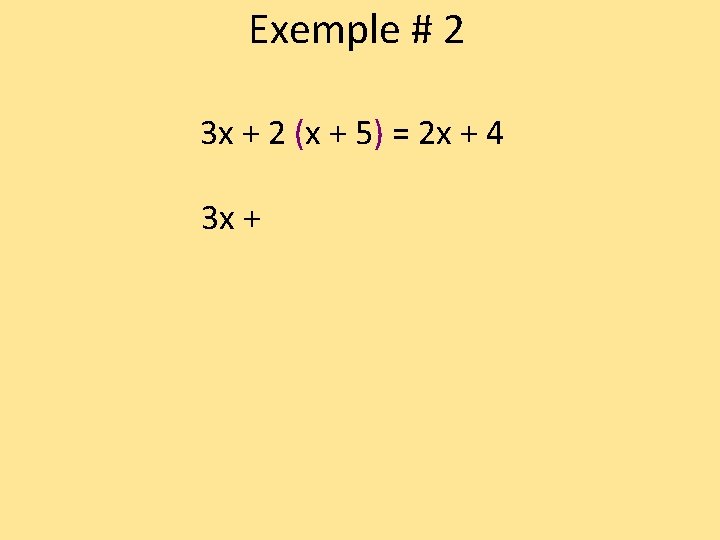
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x +

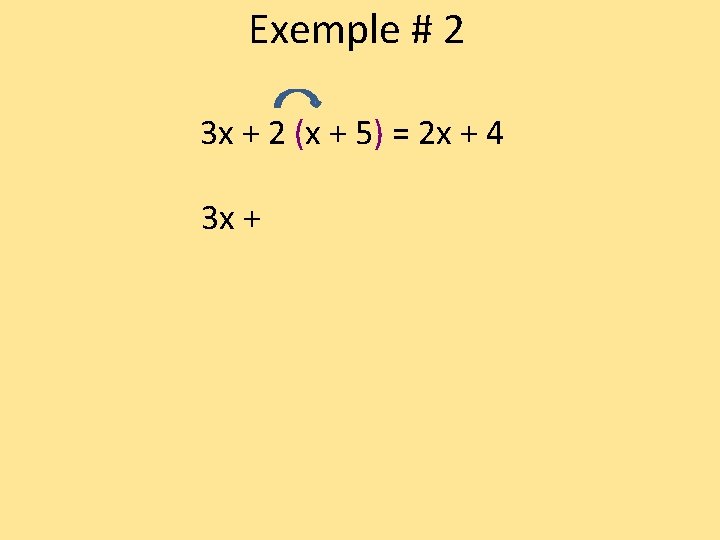
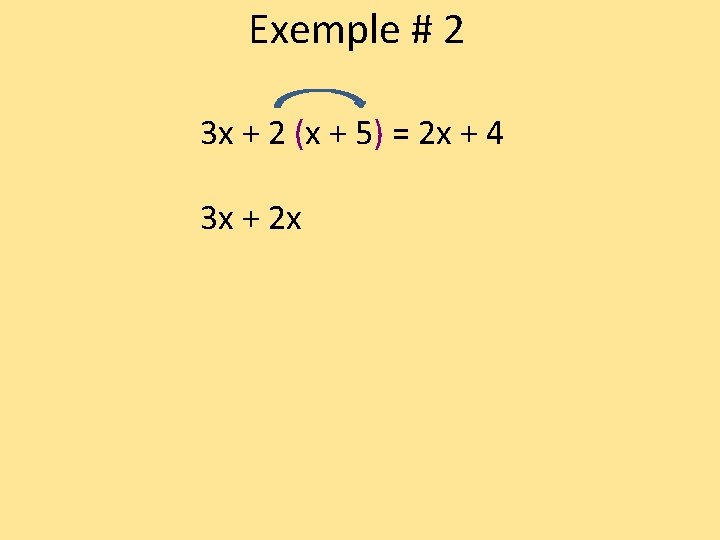
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x

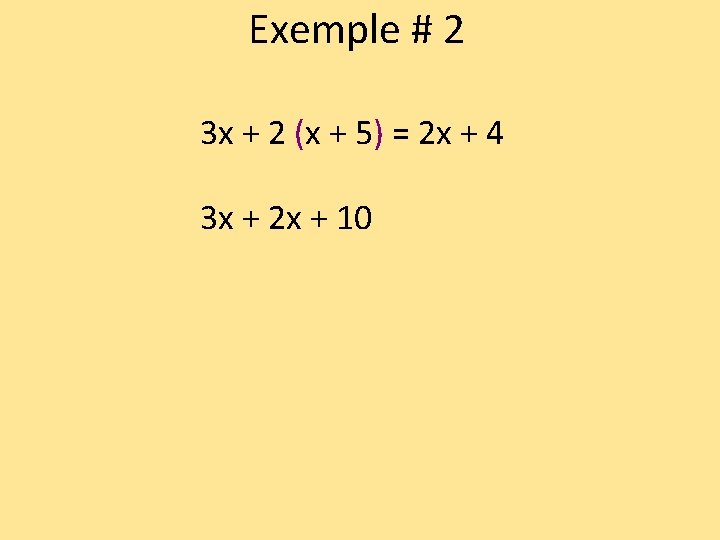
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10

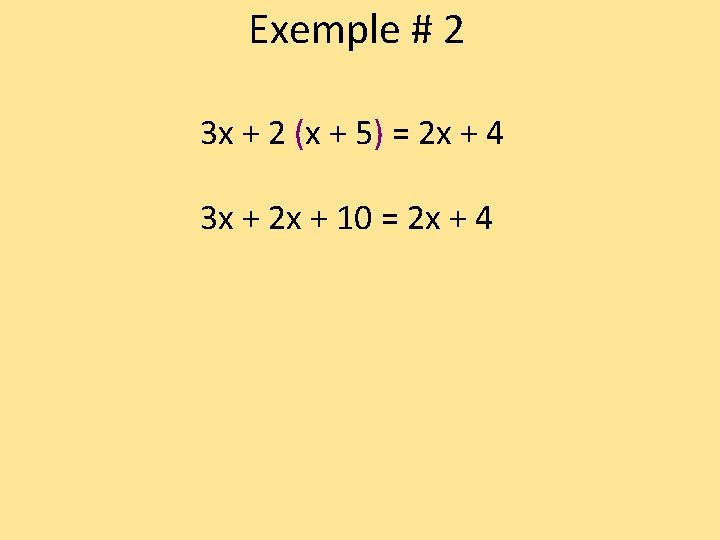
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4

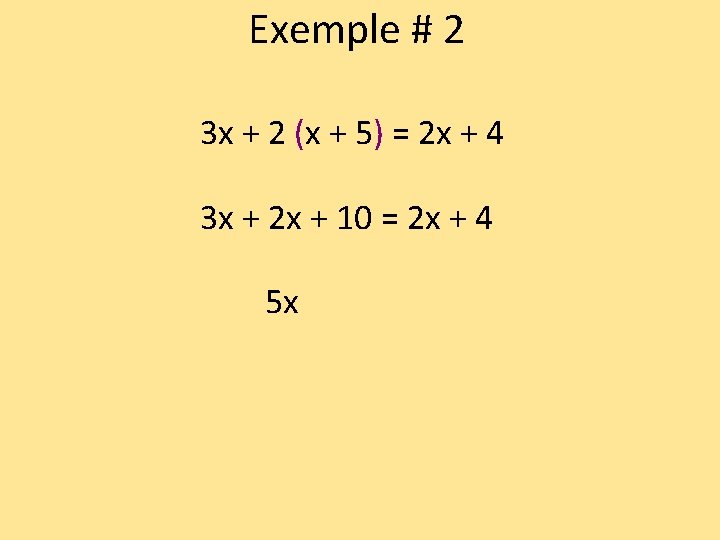
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x

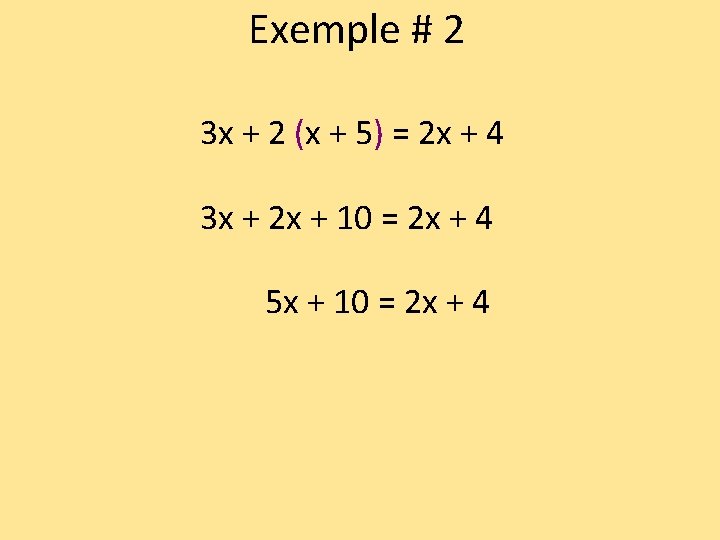
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x + 10 = 2 x + 4

Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x - 2 x + 10 = 4

Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x - 2 x = 4 - 10

Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x + 10 = 2 x + 4 3 x = 4 - 10

Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x + 10 = 2 x + 4 3 x = -6

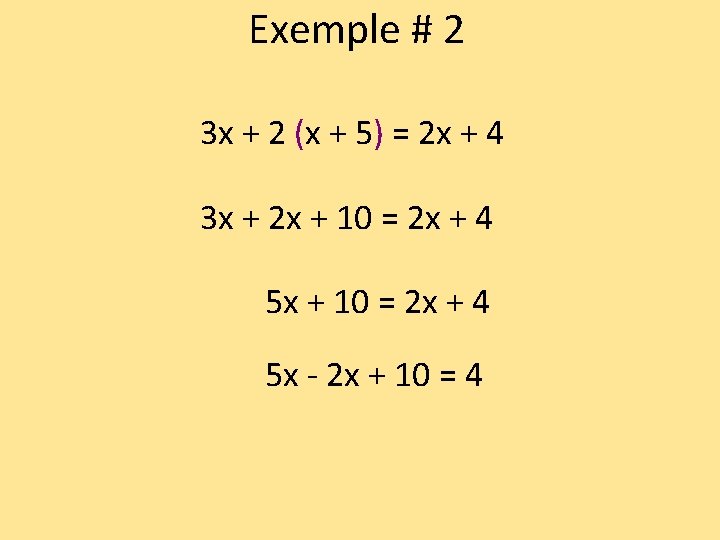
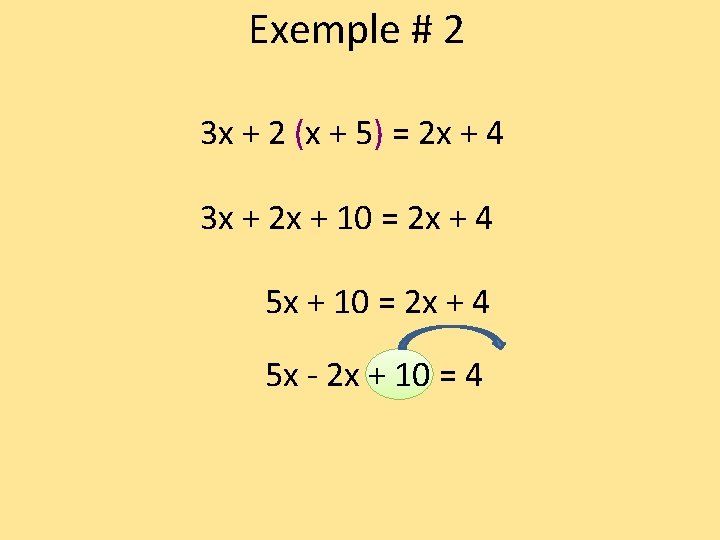
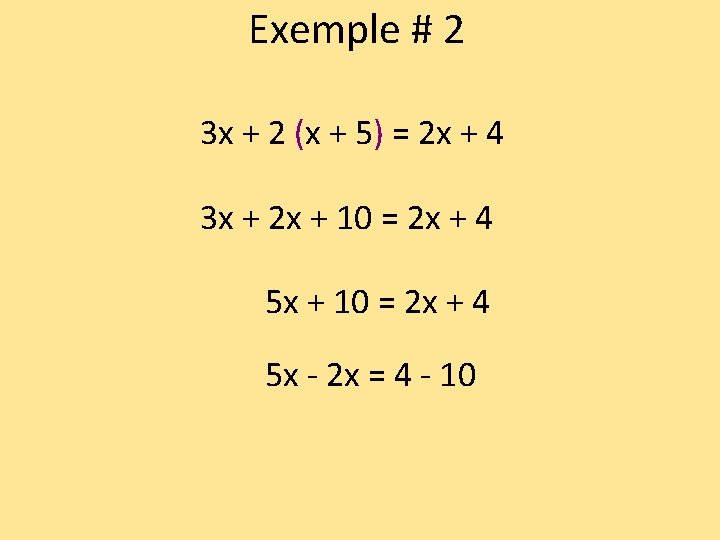
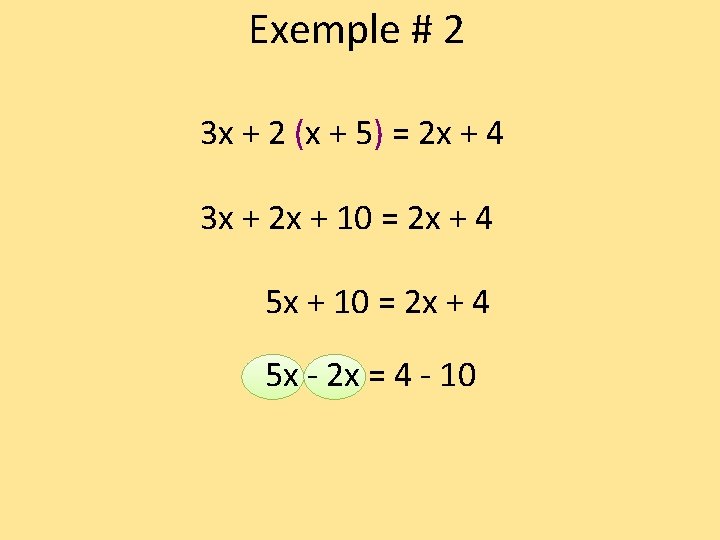
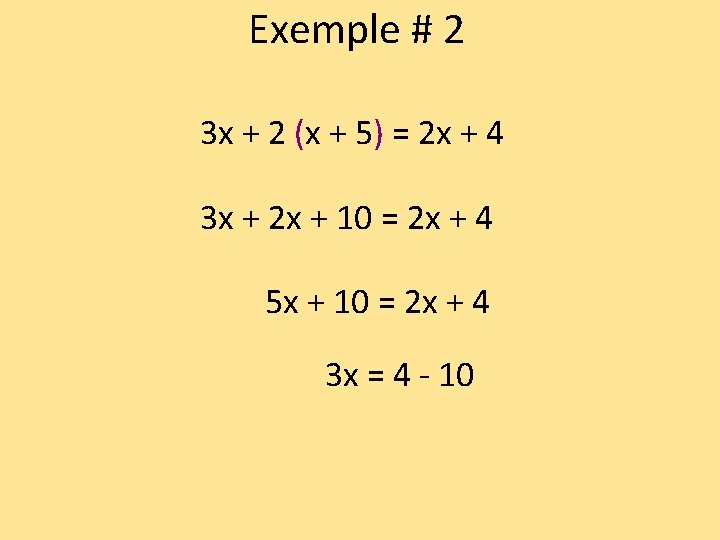
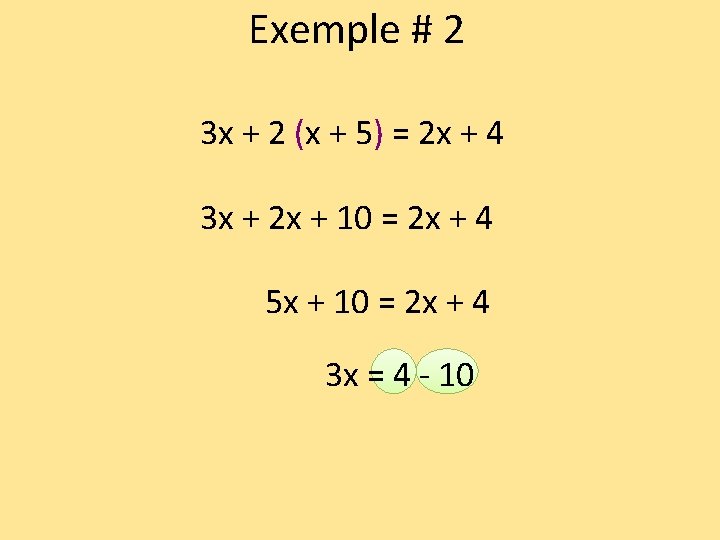
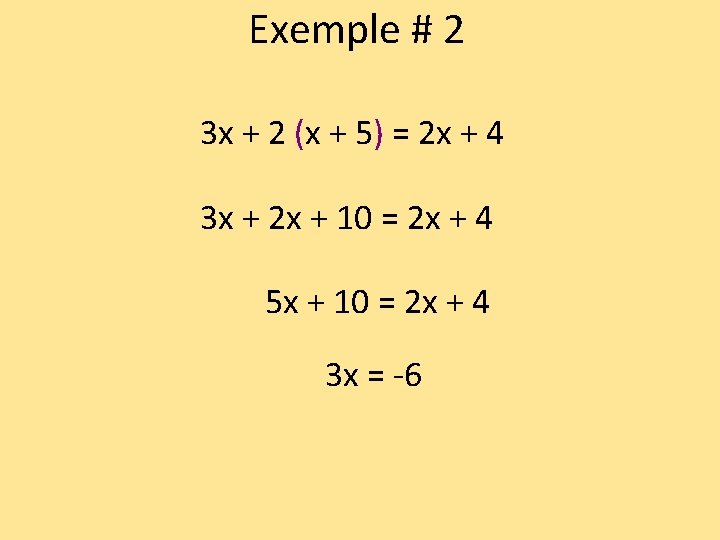
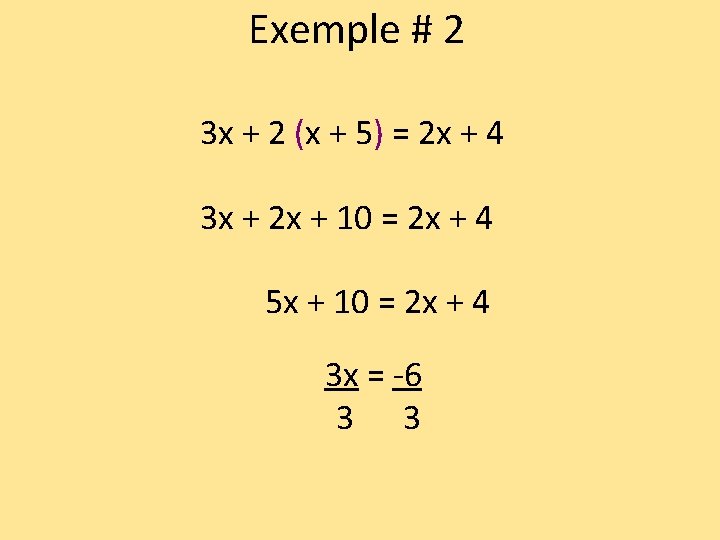
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x + 10 = 2 x + 4 3 x = -6 3 3

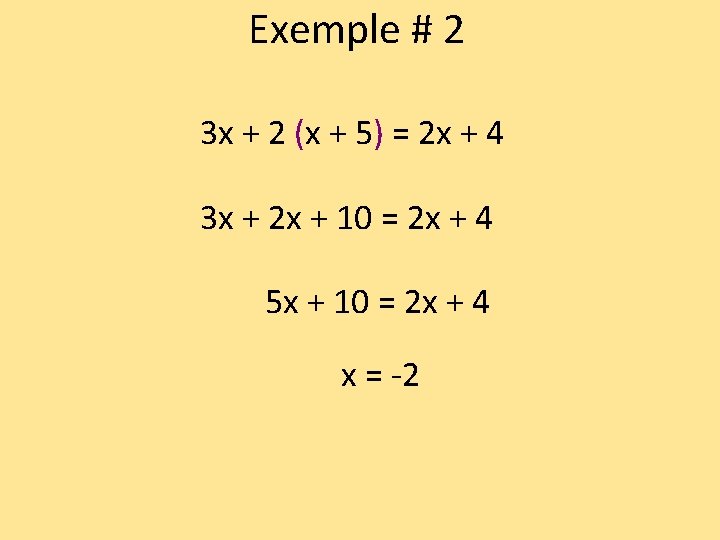
Exemple # 2 3 x + 2 (x + 5) = 2 x + 4 3 x + 2 x + 10 = 2 x + 4 5 x + 10 = 2 x + 4 x = -2

Devoirs: p. 179 nos 1 à 38 (pairs) et 39 à 43 au complet. Devoirs: p. 185 et 186 nos 2 à 68 (pairs) et nos 70 à 73 au complet