Rsolution dun programme linaire Plan Mthode graphique Mthode















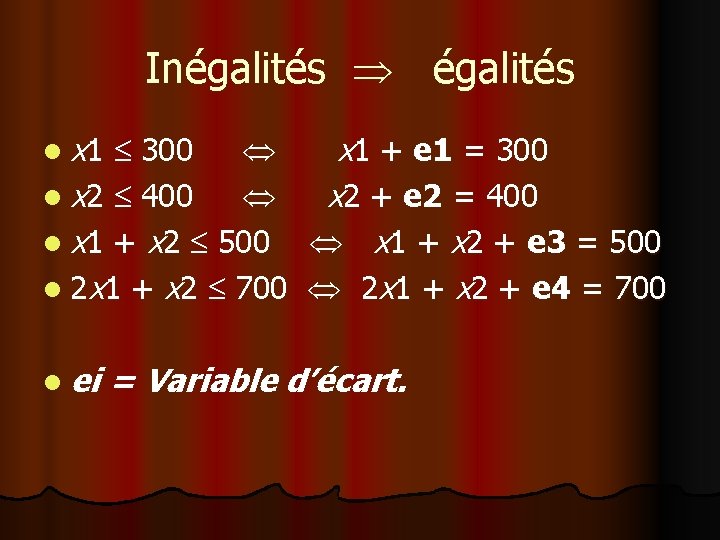




- Slides: 31

Résolution d’un programme linéaire Plan Méthode graphique Méthode du Simplexe Exercices d’application

PROGRAMME LINÉAIRE l FONCTION OBJECTIF z = c 1 x 1 +… + cnxn l Maximiser ou minimiser l Contraintes l a 11 x 1 + … + a 1 nxn ( , =, ) b 1 l a 21 x 1 + … + a 2 nxn ( , =, ) b 2 l am 1 x 1 +… + amnxn ( , =, ) bm l Contraintes de non-négativité l xj 0 ; j = 1, 2, 3, … n l avec l xj variables de décision (inconnues) l aij, bi, cj paramètres du programme linéaire

Méthode Graphique l Valable si 2 variables de décision seulement. l Le nombre de contraintes est quelconque. l Repose sur une représentation des contraintes dans un plan.

Contrainte =inégalité à 2 variables l a 1 x 1 + a 2 x 2 <= b ; b > 0, a 1 >0, a 2 > 0 x 2 b/a 2 >b Demi-espace admissible <= b b/a 1 x 1

Maximisation sous contraintes x 2 Fonction objectif Zone réalisable x 1

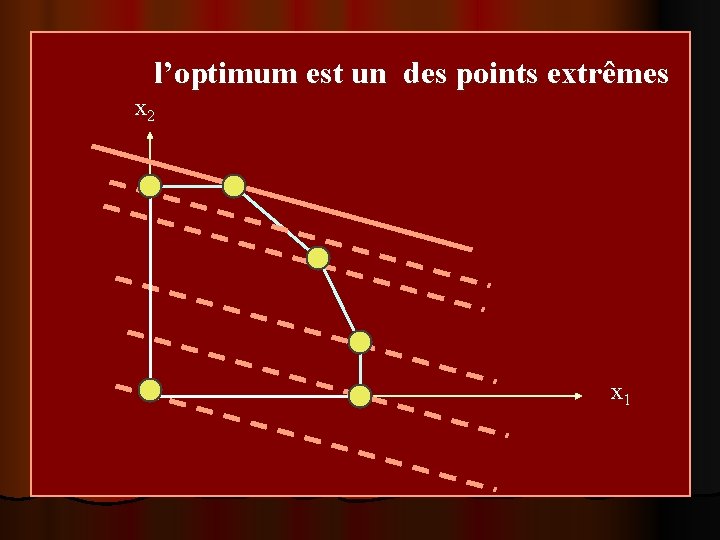
l’optimum est un des points extrêmes x 2 x 1

Exemple 1 l Maximisation du profit l Contrainte de rareté d’une ressource l Contraintes de demande

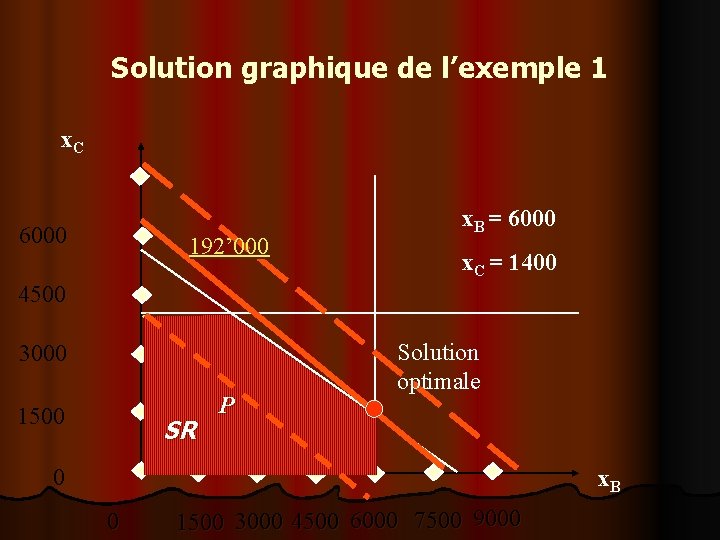
Solution graphique de l’exemple 1 x. C 6000 192’ 000 x. B = 6000 x. C = 1400 4500 3000 1500 SR P Solution optimale 0 x. B 0 1500 3000 4500 6000 7500 9000

Exemple 2 z = 3 x 1 + 5 x 2 l MAXIMISER l Contraintes : l x 1 4 2 x 2 12 l 3 x 1 + 2 x 2 18 l x 1 0 ; x 2 0 l

ZONE DE SOLUTION RÉALISABLE Zone limitée par les contraintes du problème et par les limites des variables de décision x 2 8 6 SR 4 2 0 2 4 6 8 10 x 1

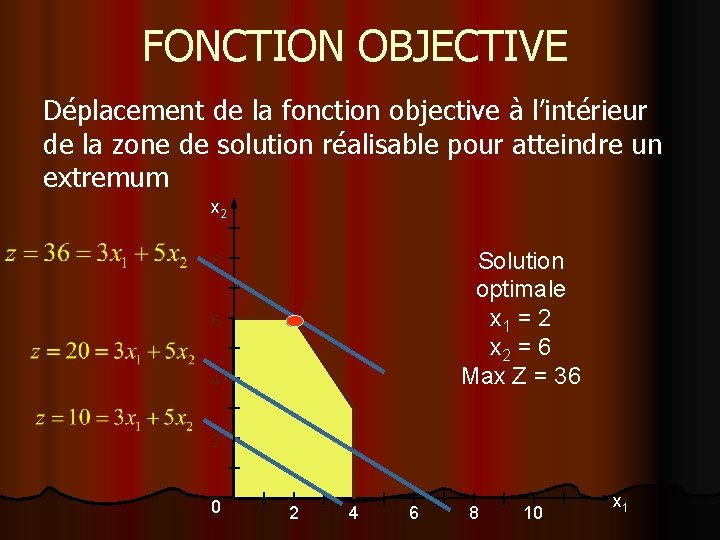
FONCTION OBJECTIVE Déplacement de la fonction objective à l’intérieur de la zone de solution réalisable pour atteindre un extremum x 2 Solution optimale x 1 = 2 x 2 = 6 Max Z = 36 8 (2, 6) 6 4 2 0 2 4 6 8 10 x 1

Exemple 3 l Maximiser Z = x 1 + 2 x 2 2 x 1 + x 2 4 x 1 + x 2 8 -x 1 + x 2 4 x 1 5 x 1 0, x 2 0

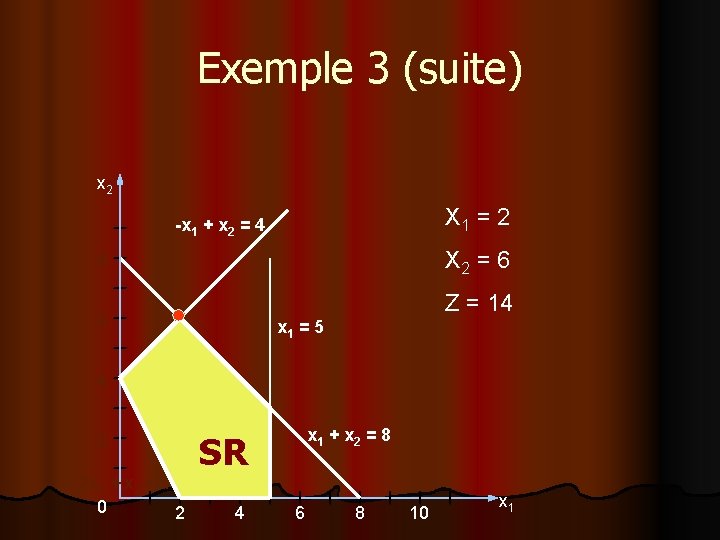
Exemple 3 (suite) x 2 X 1 = 2 -x 1 + x 2 = 4 X 2 = 6 8 Z = 14 6 x 1 = 5 4 2 2 x 1 + x 2 = 4 0 2 x 1 + x 2 = 8 SR 4 6 8 10 x 1

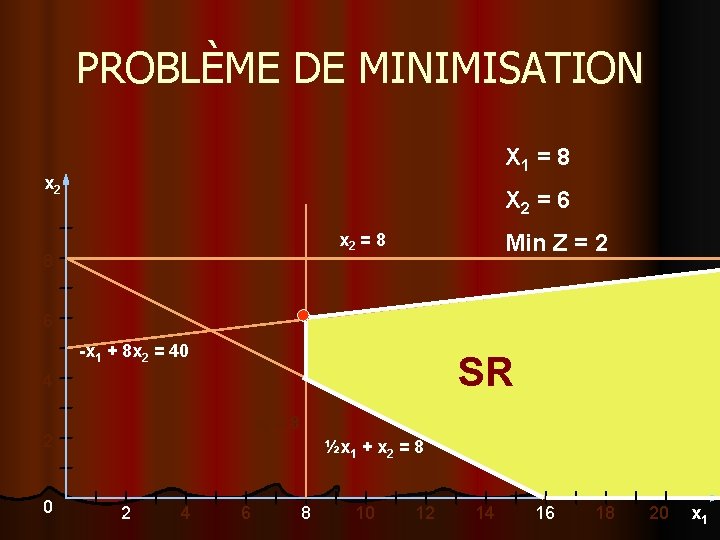
Exemple de MINIMISATION l Minimiser Z = x 1 – x 2 Sachant que : ½ x 1 + x 2 8 -x 1 + 8 x 2 40 x 1 8 x 2 8 x 1 0, x 2 0

PROBLÈME DE MINIMISATION X 1 = 8 x 2 X 2 = 6 x 2 = 8 8 Min Z = 2 6 -x 1 + 8 x 2 = 40 SR 4 x 1 = 8 2 0 ½x 1 + x 2 = 8 2 4 6 8 10 12 14 16 18 20 x 1

Cas possibles La zone SR peut être : l Vide: Contraintes contradictoires (pas de solution optimale) l borné : le problème possède toujours au moins une solution optimale l non borné : selon la fonction objectif l Si MIN : il y a une solution finie l Si MAX : Solution non bornée

Le nombre de solutions optimales ? - Une seule. - Une infinité : si deux sommêts réalisent l’optimum (tout le segment reliant les deux sommêts optimaux)

Méthode du simplexe l Méthode algébrique l Méthode itérative

Etapes l Forme standard du PL l Tableau de départ du simplexe l Application de l’algorithme du simplexe

Forme standard d’un PL l Maximiser Z = 7 x 1 + 5 x 2 Sachant que : l x 1 300 l x 2 400 l x 1 + x 2 500 l 2 x 1 + x 2 700 l x 1 0 l x 2 0
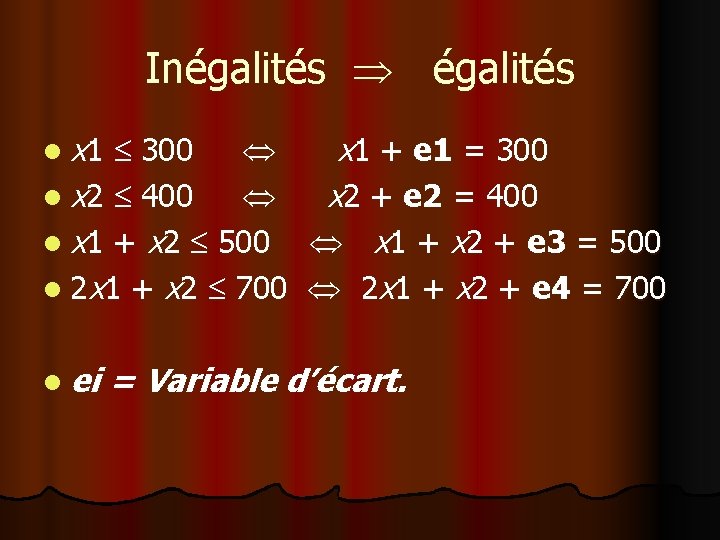
Inégalités l x 1 300 x 1 + e 1 = 300 l x 2 400 x 2 + e 2 = 400 l x 1 + x 2 500 x 1 + x 2 + e 3 = 500 l 2 x 1 + x 2 700 2 x 1 + x 2 + e 4 = 700 l ei = Variable d’écart.

l Maximiser Z = 7 x 1 + 5 x 2 Sachant que : l x 1 + e 1 =300 l x 2 + e 2 = 400 l x 1 + x 2 + e 3 = 500 l 2 x 1 + x 2 + e 4 = 700 l x 1 0 ; x 2 0 l ei 0


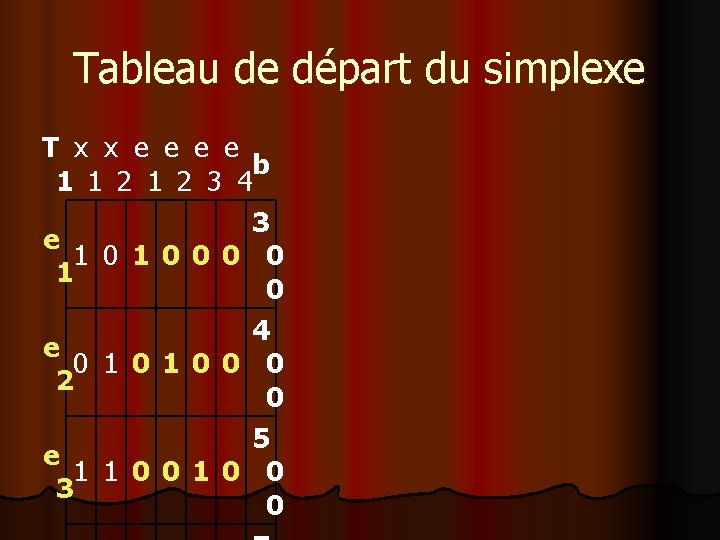
Tableau de départ du simplexe T x x e e b 1 1 2 3 4 3 e 1 0 0 0 0 1 0 4 e 0 1 0 0 0 2 0 5 e 1 1 0 0 3 0

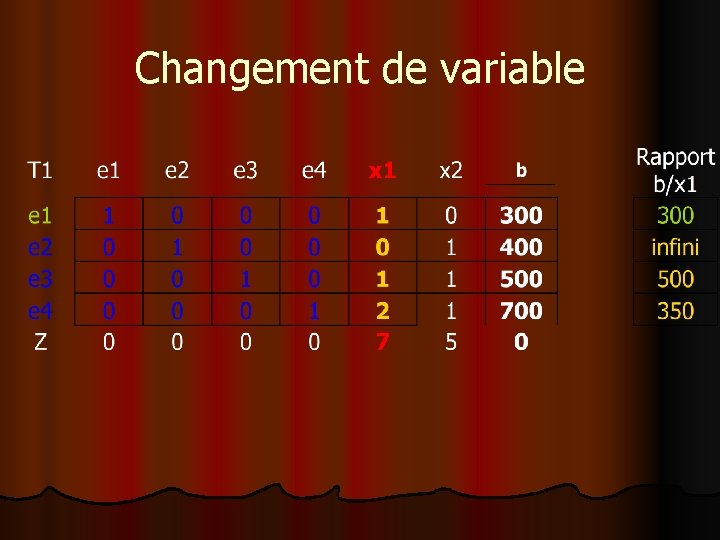
Changement de variable

Deuxième tableau

Changement de variable

Troisième tableau

Changement de variable

Quatrième tableau

Solution optimale En base : x 1 = 200 e 2 = 100 e 1 = 100 x 2 = 300 e 3 = e 4 = 0 (hors base) Max Z = 2900