RSA Variants 1 Information Security Group ICU Rabin

RSA Variants 1 © Information Security Group, ICU

Rabin Scheme(I) q Scheme m Select p, q = 3 mod 4 m n=pq m public =n, secret=p, q m y= ek(x)=x (x+b) mod n m x=dk(y)= mod n m Choose one of 4 solutions using redundancy ( p. 211) q Square root m No known deterministic poly alg. to compute square roots of quadratic residues mod p. (but Las Vegas Algorithm exists) m If p=3 mod 4, ( C(p+1)/4)2=C mod p m If n=pq, there are four square roots of a quadratic residue. q Security = Factorization (provable security) 2 © Information Security Group, ICU

Rabin Scheme(II) (Ex) p=7, q=11, n=p q=77, b=9 ek(x)=x(x+9) mod 77 dk(y)= (1+y)-43 mod 77 (Decryption) (1) If ciphertext y=22, 23 mod 77 10, 32 mod 77 (2) Then, choose one of 10 -43 mod 77=44, (77 -10)-43 mod 77=24, 32 -43 mod 77=66, (77 -32)-43 mod 77=2 using redundancy (not 1: 1) 3 © Information Security Group, ICU

Discrete Logarithm Problem 4 © Information Security Group, ICU

Cryptography based on Groups q G is a group under a binary operation * m. G is closed under * m* is associative m. Existence of identity and inverse m(Abelian) a*b=b*a for arbitrary a and b in G q Example: (Z, +), ((Z/p)*, ) q Discrete Logarithm Problem (DLP) on G m. G is a group and h, g G m. Determine the least positive integer x satisfying h=gx 5 © Information Security Group, ICU

Diffie-Hellman Key Exchange q Obj: Agree on shared secret over insecure channel q Key Generation m. Take an Abelian group G under which DLP is intractable m. Take a generator g of G q Alice m. Take a random integer a and send ga to Bob q Bob m. Take a random integer b and send gb to Alice q Shared Key: gab=(ga)b=(gb)a 6 © Information Security Group, ICU

Hard Problems on a group q G: Abelian group with prime order p and g G m. DLP: Given h G, find x s. t. gx=h m. CDH: Given g, ga, gb find gab m. DDH: Given g, ga, gb, gc decide if c=ab mod p m. The problems can be defined on a group with composite order, but their security depends on the largest prime divisor of the order. q Problem Reductions m. IFP > RSA m. DL > CDH > DDH 7 © Information Security Group, ICU

Which Group is Used q Criteria m Abelian groups m The group operation should be simple to realize m DLP is intractable q Consider the group operation given by simple algebraic formulae m G is a commutative finite algebraic group m Equivalent to the product of copies of (add or mult. ) finite fields and Jacobians of curves. q Instances m The multiplicative group of Finite Fields m Elliptic Curves m Hyperelliptic Curves m Class group of orders of number fields (Buchman and Williams) Binary Quadratic form 8 © Information Security Group, ICU

Attack on DLP 9 © Information Security Group, ICU

Discrete Logarithm(II) q Exhaustive Search : O(p) time, O(1) space q Precomputed Table : O(1) time, O(p) space q Time-memory Tradeoff by Shanks’ BSGS: O(1) time, O(p) pre-computation, O(p) memory q Square-root method m. Can be applied to any DLP m. Pollard rho: random walk by one kangaroo m. Pollard lambda: Use two kangaroo’s 10 © Information Security Group, ICU

Shanks’ Baby Step Giant Step Input : p, , , Output : a where a = mod p. Let m = (p-1) 1. compute mj mod p, 0 j m-1 2. sort m ordered pairs (j, mj mod p) w. r. t. 2 nd coordinates, obtaining list L 1 3. compute -i mod p, 0 i m-1 4. sort m ordered pairs (i, -i mod p) w. r. t. 2 nd coordinates, obtaining list L 2 5. find a pair (j, y) L 1 and a pair (i, y) L 2 (i. e. , a pair having identical 2 nd coordinates) 6. output mj +i mod(p-1). ( mj =y= -i, mj +i= log =mj+i) * Complexity : O(m) time, O(m) memory 11 © Information Security Group, ICU

Shanks’ algorithm : Example (Ex. ) p=809, find log 3525. 1. =3, =525, m = (808) =29 2. 29 mod 809 = 99. 3. ordered pairs (j, 99 j mod 809) for 0 j 28 (0, 1), …, (10, 644), …, (28, 81). 4. ordered pairs (i, 525 x(3 i)-1 mod 809), 0 i 28 (0, 525), …, (19, 644), …, (28, 163). 5. find match (10, 644) in L 1 and (19, 644) in L 2 6. thus, log 3525 = 29 x 10 + 19 =309 7. (Confirmation) 3309 = 525 mod 809 12 © Information Security Group, ICU

Pohlig-Hellman Algorithm q Pohlig-Hellman Algorithm m. Find a mod p-1 s. t. h=ga where g has the order p m. Compute p-1= i=1 k qici m. Compute a mod qici (1 i k) m. Find a mod (p-1) by CRT m. If p-1 is smooth, the complexity is small. 13 © Information Security Group, ICU

Index Calculus Method m Input: generator g of cyclic group G of order n and h=ga in G m Output: a mod n m (Select a factor base S) Choose a subset S={p 1, p 2, . . , pt} of F s. t. a significant proportion of all elements in G can be efficiently expressed as a product of elements from S m (Collect linear relations) 1. Select a random integer k with 0=<k<n, and compute gk 2. Try to write gk as a product of primes in S 3. Repeat steps 1 and 2 until t+c relations are obtained (c =10) m (Find the logarithms of elements in S) 1. Working modulo n, solve the linear system of t+c equations (in t unknowns) to obtain loggpi m (Compute a) 1. Select a random integer k with 0=<k<n, and compute hgk 2. Write hgk as a product of elements in S 3. Compute a from the above relation and loggpi (1=<i=<t) 14 © Information Security Group, ICU

Complexity q Let Lq( , c)=exp(c(log q) (loglog q)1 - ) m. If =0, polynomial time algorithm m. If >=1, exponential time algorithm m. If 0< <1, subexponential time algorithm q Square-root method: exp. time q Index Calculus m. G=Fp : Lp [1/3, c] m. G=F 2 m: L 2 m[1/2, c] m. G=Elliptic Curve: Not working 15 © Information Security Group, ICU

ECC 16 © Information Security Group, ICU

What is an Elliptic Curve? q Elliptic Curves: my 2 + xy = x 3 + a 2 x 2 + a 6 (a 2 , a 6 GF(q)) q Elliptic Curve is not an ellipse => Cubic Curve q Elliptic Curve: m. E(Fq)={(x, y) Fq | y 2 + xy = x 3 + a 2 x 2 + a 6 } {O} q E(Fq) forms a group under addition 17 © Information Security Group, ICU

Operation of EC q Addition m (x 1, y 1) + (x 2, y 2) = (x 3, y 3) Ø x 3 = A 2 + A - a 2 - x 1 - x 2, y 3 = - (A + a 1 ) x 3 - B - a 3 Ø A = ( y 2 - y 1 ) / ( x 2 - x 1 ), B = ( y 1 x 2 - y 2 x 1 ) / ( x 2 - x 1 ) if x 1 x 2 q Number of operations in finite field needed for an addition of points in EC m Mul : 4 m Div : 2 m Add or Sub : 9 q Integer Multiplication : m n. P = P + … + P (n Z, P E(F 2 n)) m 3 P = P + P 18 © Information Security Group, ICU

Diffie-Hellman Key Exchange q Obj: Agree on shared secret over insecure channel q Key Generation m Take a finite field Fq and an elliptic curve E over Fq m Take a generator P of E(Fq) q Alice m Take a random integer a and send a. P to Bob q Bob m Take a random integer b and send b. P to Alice q Shared Key: ab. P=a(b. P)=b(a. P) or its x-coordinate q a. P or b. P can be identified with its x-coor. plus one bit 19 © Information Security Group, ICU

Hard Problems in ECC q Hard Problem m DL Problem: find a in Z/n from (P, a. P) m CDH Problem: find ab. P from (P, a. P, b. P) m DDH Problem: determine whether c. P=ab. P from (P, a. P, b. P, c. P) q Consider a DLP on a group of order p m DLP is equivalent to DHP if we can find an elliptic curve over Fp whose number of points are smooth. m DDH is solved in poly. time on supersingular curve q DLP = DHP > DDHP=poly. time m The second equality holds for supersingular EC 20 © Information Security Group, ICU

Security of ECC q General Attack m Baby-Step Giant-Step for E(Fq): O( q log q) m Pollard rho for E(Fq): O( q) m Pohlig-Hellman m Index calculus (not applicable) q Special Attack m Subexponential time: singular or supersingular m Polynomial time: anomalous q Candidate of an EC for secure DLP m Avoid singular, supersingular, or anomalous curve m The order must be divided by a large prime factor m Then breaking ECC takes exponential time!! 21 © Information Security Group, ICU

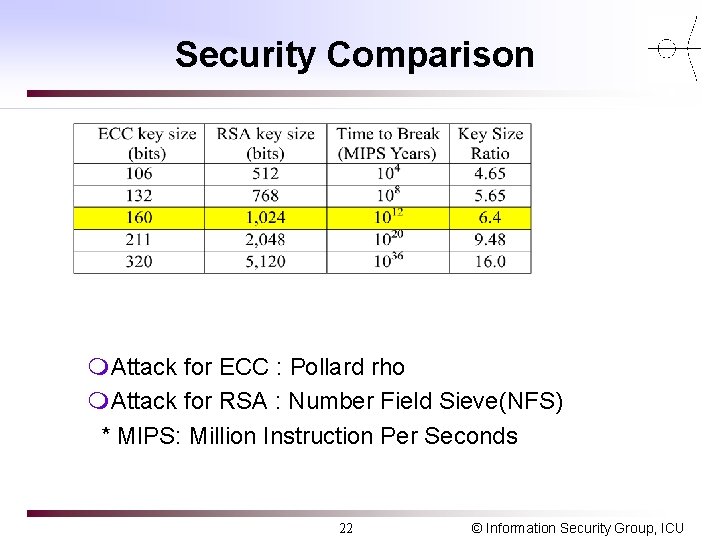
Security Comparison m. Attack for ECC : Pollard rho m. Attack for RSA : Number Field Sieve(NFS) * MIPS: Million Instruction Per Seconds 22 © Information Security Group, ICU