RSA Shors Algorithm Math Background by Drs Charles

RSA & Shor’s Algorithm Math Background by Drs. Charles Tappert and Ron Frank The information presented here comes primarily from Wikipedia

RSA & Shor’s Algorithm Math – LCM n The least common multiple (LCM) of 2 numbers is the smallest number that they both divide n n n One way to find the least common multiple of two numbers is to first list the prime factors of each number Then multiply each factor the greatest number of times it occurs in either number Example: find the LCM of 30 and 45 n n List the prime factors of each number 30 = 2 × 3 × 5, 45 = 3 × 5 Multiply each factor the greatest number of times it occurs in either number LCM(30, 45) = 2 × 3 × 5 = 90

RSA & Shor’s Algorithm Math – GCD n Greatest Common Divisor (GCD) of two integers A and B is the largest integer that divides both A and B n n Euclidean Algorithm quickly finds GCD of two integers Write A in quotient remainder form (A = B⋅Q + R) Find GCD(B, R) using this method since GCD(A, B)=GCD(B, R) Iterate until A or B goes to zero, answer is non-zero number

RSA & Shor’s Algorithm Math – GCD n Example: Find GCD of 270 and 192 with Euclidean Alg n n n n n Use long division to find that 270/192 = 1 with a remainder of 78. We can write this as: 270 = 192 * 1 +78 Find GCD(192, 78), since GCD(270, 192)=GCD(192, 78) Use long division to find that 192/78 = 2 with a remainder of 36. We can write this as 192 = 78 * 2 + 36 Find GCD(78, 36), since GCD(192, 78)=GCD(78, 36) Use long division to find that 78/36 = 2 with a remainder of 6. We can write this as 78 = 36 * 2 + 6 Find GCD(36, 6), since GCD(78, 36)=GCD(36, 6) Use long division to find that 36/6 = 6 with a remainder of 0. We can write this as 36 = 6 * 6 + 0 Find GCD(6, 0), since GCD(36, 6)=GCD(6, 0) B =0, GCD(6, 0)=6

RSA & Shor’s Algorithm Math – Euler’s totient function φ(n) counts the positive integers up to n that are relatively prime to n φ(n) is a multiplicative function – if two numbers m and n are relatively prime, then φ(mn) = φ(m)φ(n) First 1000 φ(n) values n (Khan Academy video) n When p is prime (top line), φ(p) = p − 1 n n

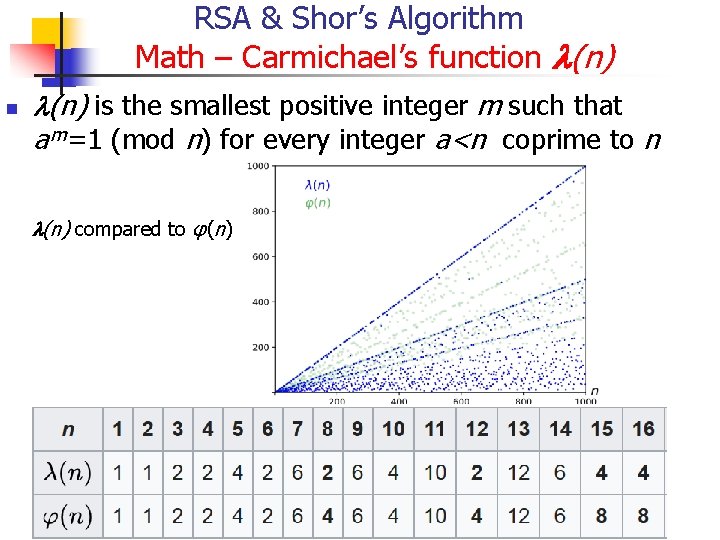
RSA & Shor’s Algorithm Math – Carmichael’s function l(n) is the smallest positive integer m such that a m=1 (mod n) for every integer a<n coprime to n l(n) compared to φ(n)

RSA & Shor’s Algorithm Math – Carmichael’s function l(n) n Numerical example n Carmichael's function at 8 is 2, i. e. l (8) = 2 because for any number a coprime to 8 it holds that a 2 ≡ 1 n n n Namely, 12 = 1 (mod 8), 32 = 9 ≡ 1 (mod 8), 52 = 25 ≡ 1 (mod 8) and 72 = 49 ≡ 1 (mod 8) Euler's totient function at 8 is 4, i. e. φ (8) = 4 because there are 4 numbers lesser than and coprime to 8 (1, 3, 5, and 7) Euler's theorem assures that a 4 ≡ 1 (mod 8) for all a coprime to 8, but 4 is not the smallest such exponent

RSA & Shor’s Algorithm Math – Multiplicative order n n Given integers a and n with gcd(a, n) = 1, the multiplicative order of a modulo n is the smallest positive integer k with a k = 1 (mod n) Example: a = 4, n = 7, so the powers of 4 mod 7 are: The smallest positive integer k such that 4 k = 1 (mod 7) is 3

RSA & Shor’s Algorithm Math – Multiplicative order properties n n n The powers of a can only take a finite number of different values modulo n, so according to the pigeonhole principle there must be two powers, say s and t with s > t, such that as ≡ at (mod n) Since a and n are coprime, then a has an inverse a− 1 and we can multiply both sides of the congruence with a−t, yielding as−t ≡ 1 (mod n) Because the concept of multiplicative order is a special case of the order of group elements, ordn(a) always divides Euler's totient function φ(n) and Carmichael function λ(n)