RSA Example A small and insecure example Stinson

RSA Correctly Decrypts Need to show that for any plaintext m 2 Zn, (me)d

Chinese Remainder Theorem Suppose m 1, …, mk are pairwise relatively prime positive integers,

Chinese Remainder Theorem Example: We want to find x that satisfies the following congruencies:

RSA Correctly Decrypts, part 2 If m is not divisible by p: If m

RSA Correctly Decrypts, part 2 So, for all m: (me)d ≡ m (mod p).

RSA: Computational Issues We showed that RSA works (i. e. , correctly decrypts). But…

RSA: Computational Issues Want: algorithms polynomial in the length of n. What is the

RSA: Computational Issues Modular Arithmetic: Give upper bounds (using the big-Oh notation) on the

Slides: 11

Download presentation

RSA Example A small (and insecure) example [Stinson]: - Bob: - chooses p = 101, q = 113 - computes n = pq = 11413 and Á(n) = (p-1)(q-1) = 11200 - chooses e = 3533 (note: gcd(e, Á(n))=1) - computes d = e-1 mod Á(n) = 6597 - publishes n and e (keeps p, q, and d private) - Alice wants to send 9726 to Bob: - computes 9726 e mod n = 97263533 mod 11413 = 5761 - sends 5761 to Bob - Bob: - computes 5761 d mod n = 57616597 mod 11413 = 9726

RSA Correctly Decrypts Need to show that for any plaintext m 2 Zn, (me)d mod n = m. We will need some number theory: If gcd(m, n)=1: - we will use Euler’s Theorem (pg 81): If gcd(a, n)=1, then aÁ(n) ´ 1 (mod n) - can we conclude that (me)d mod n = m ? If gcd(m, n)>1: - we will use the Chinese Remainder Theorem (Section 3. 4)

Chinese Remainder Theorem Suppose m 1, …, mk are pairwise relatively prime positive integers, and suppose a 1, …, ak are integers. Then the system of congruences x ≡ ai (mod mi) (1 ≤ i ≤ k) has a unique solution modulo M = m 1 m 2…mk, which is given by x = i=1…k ai. Miyi mod M, where Mi = M/mi and yi = Mi− 1 mod mi, for 1 ≤ i ≤ k.

Chinese Remainder Theorem Example: We want to find x that satisfies the following congruencies: x ≡ 5 (mod 7) x ≡ 3 (mod 11) x ≡ 10 (mod 13) The solutions is unique mod ____: x=

RSA Correctly Decrypts, part 2 If m is not divisible by p: If m is divisible by p:

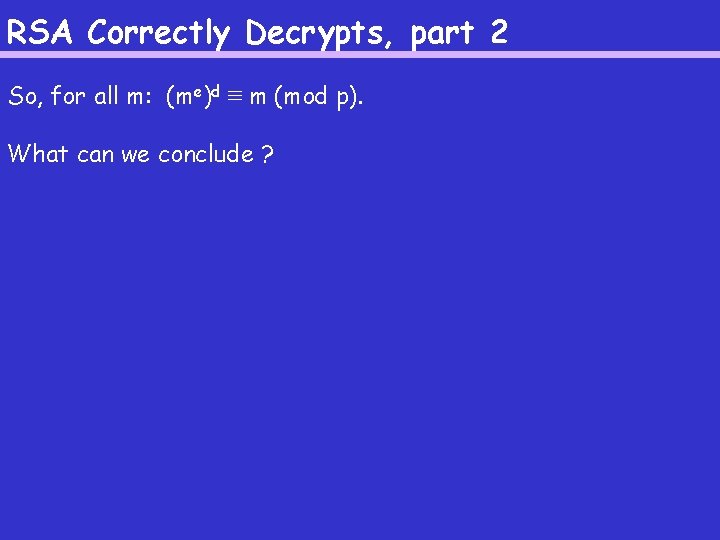
RSA Correctly Decrypts, part 2 So, for all m: (me)d ≡ m (mod p). What can we conclude ?

RSA: Computational Issues We showed that RSA works (i. e. , correctly decrypts). But… Can we actually compute me mod n for very large numbers ?

RSA: Computational Issues Want: algorithms polynomial in the length of n. What is the length of n ? Note: typically when estimating the running time of an algorithm, arithmetic operations are counted as taking constant time – but this is NOT feasible in cryptography where the numbers can be very large (recommended size of p, q in RSA: 1024 bits)

RSA: Computational Issues Modular Arithmetic: Give upper bounds (using the big-Oh notation) on the running time of the following operations in Zn: - addition - difference - multiplication - exponentiation - gcd - inverse - RSA encryption - RSA decryption