Royal Holloway University of London Department of Computer

Royal Holloway, University of London Department of Computer Science 27 June 2019 Connections Between Algorithms, Proofs and Cryptography Ján Pich University of Oxford

Goal: understand the power of algorithms and reasoning answer ‘‘universal’’ questions, e. g. Theorem Proving, Learning Algorithms 2

My Research Area Foundations of Computer Science Computational Complexity efficiency of algorithms and their limits SAT solving, QBF solving my publications: LICS’ 18, CCC’ 19, FOCS’ 19, JACM, APAL, LMCS, etc. proof complexity Applications in Cryptography, Learning algorithms, Pseudorandomness etc. 3

1. Quick Background 4

Fundamental Questions P vs NP: efficiency of computation Cook Levin NP vs co. NP: efficiency of proofs Can we learn efficiently? . . . Valiant 5

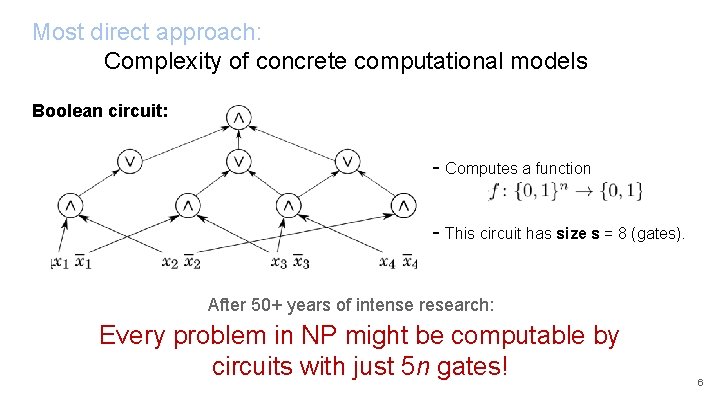
Most direct approach: Complexity of concrete computational models Boolean circuit: - Computes a function - This circuit has size s = 8 (gates). After 50+ years of intense research: Every problem in NP might be computable by circuits with just 5 n gates! 6

Golden Age of Circuit Lower Bounds Circuits of polynomial-size and constant depth cannot compute PARITY Ajtai (1983) Furst-Saxe-Sipser (1984) Adding PARITY gates does not help much Razborov (1987) Smolensky (1987) Circuits of polynomial-size without negation gates cannot solve problems in P Razborov (1985) etc. P ≠ NP behind the corner? 7

Fall of the Circuit Lower Bounds Program Natural proofs of Razborov and Rudich (1994): All known circuit lower bounds on explicit Boolean functions are very constructive (imply efficient algorithms recognizing hard Boolean functions) Barrier: Cryptography works �no natural proof of P ≠ NP proof: natural proof of P ≠ NP distinguishes random functions from pseudorandom functions (those with small circuits) 8

New Connections Between Logic and Cryptography Comprehensive understanding of barriers in the framework of Mathematical Logic: Razborov (1995). Cryptography works �P ≠ NP unprovable in theory S²₂(�� ) Rreformulated: Cryptography works �P ≠ NP hard to prove in constructive propositional proof systems. Problem: Krajíček-Pudlák (1998). Strong proof systems not constructive unless RSA insecure. 9

Strong Proof Systems Frege - textbook system for propositional logic Tautologies hard for Frege �NP ≠ co. NP hard = long proofs Razborov’s conjecture (2003): Standard hardness assumption �Pseudorandom generators hard for Frege and P ≠ NP hard as well 10

2. My Results 11

P. [2010] Razborov’s conjecture holds for constructive proof systems e. g. : Resolution (the underlying system of most existing SAT solvers) Cutting planes (captures linear programming) - Previously only special pseudorandom generators were known to be hard for some weak systems. However, recall: Frege not constructive unless crypto breaks (Krajíček-Pudlák) 12

Approaching Strong Systems Conceptual shift: PV⊢ P ≠ NP? PV: Cook’s theory (1975) formalizing p-time reasoning. PV � ``uniform’’ Frege P. [2013] Theories weaker than PV cannot prove P ≠ NP unless hardness breaks. 13

P. [2014] PV is powerful: it proves the PCP theorem: mathematical proofs can be verified whp by reading just 20 bits. - one of the highest achievements of Complexity theory. implementations in cryptocurrencies sophisticated proof: a culmination of many innovative ideas (error-correcting codes, expanding graphs, interactive proofs, etc. ) P. [2014] PCP theorem can be expressed by tautologies having short Frege proofs. let’s reconsider positive aspects of the provability of lower bounds 14

Lower Bounds Imply Learning Carmosino Impagliazzo Kabanets Kolokolova (2016). Natural proofs �learning algorithms Learning model: access a function computable by a small circuit output a circuit computing the function whp P. - Muller [2017]. Efficiently generating Frege proofs of known circuit lower bounds more suitable for learning from random examples 15

What have we seen so far? Barrier Results: hardness of P ≠ NP (connections to Cryptography) Upper Bounds: constructions of short proofs (connections to Learning Algorithms) Next: new approach to P ≠ NP 16

Emergence of Hardness Magnification P. - Muller [2017]. (proof complexity magnification) weak system strong system P ≠ NP slightly hard for constant-depth Frege �P ≠ NP hard for Frege Oliveira Santhanam (2018). (circuit complexity magnification) “MCSP” hard for linear size circuits � P ≠ NP MCSP: given a function, decide if computable by a small circuit (ancient & fundamental problem) Hardness magnification overcomes natural proofs barrier! 17

New Hope Oliveira-P. -Santhanam [2018] MCSP hard for linear-size circuits � P ≠ NP MCSP hard for subquadratic-size formula MCSP hard for linear-size almost formula The assumption holds for PARITY � NP hard for polynomial-size formulas but MCSP is much harder than PARITY! 18

3. Future Directions - Explain hardness magnification (collaborations: Oxford, MIT) consequences for cryptography, pseudorandomness etc. - Strengthen connections to learning (collaborations: Toronto, Warwick) turn impossibility results into new learning algorithms - Implement in SAT solvers (collaborations: Waterloo, Jena) simulate learning algorithms by SAT solving lower bounds Royal Holloway: great place for collaborations on these topics! (e. g. Iddo Tzameret, Magnus Wahlström, Gregory Gutin) THANK YOU! 19