Routing Link State Algorithm Networking CS 3470 Section

Routing: Link State Algorithm Networking CS 3470, Section 1

Routing Forwarding versus Routing Forwarding: To select an output port based on destination address and routing table Routing: Process by which routing table is built

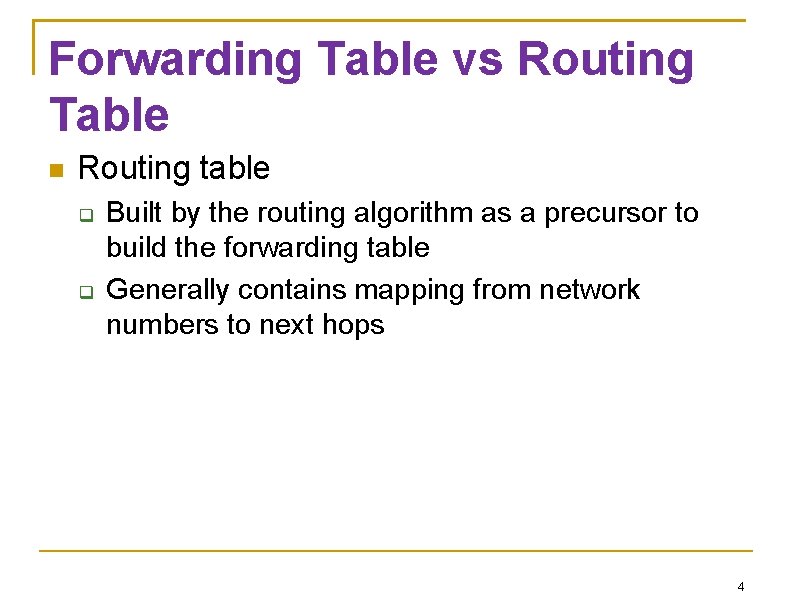
Forwarding Table vs Routing Table Forwarding table Used when a packet is being forwarded Must contain enough information to forward A row in the forwarding table contains Mapping from a network number to outgoing interface MAC or Ethernet address of the next hop

Forwarding Table vs Routing Table Routing table Built by the routing algorithm as a precursor to build the forwarding table Generally contains mapping from network numbers to next hops 4

Routing An autonomous system (AS) is a network that is administrated independently of other ASs Backbone service providers and regional providers form their own ASs Can run their own (different) routing algorithms Also called routing domains 5

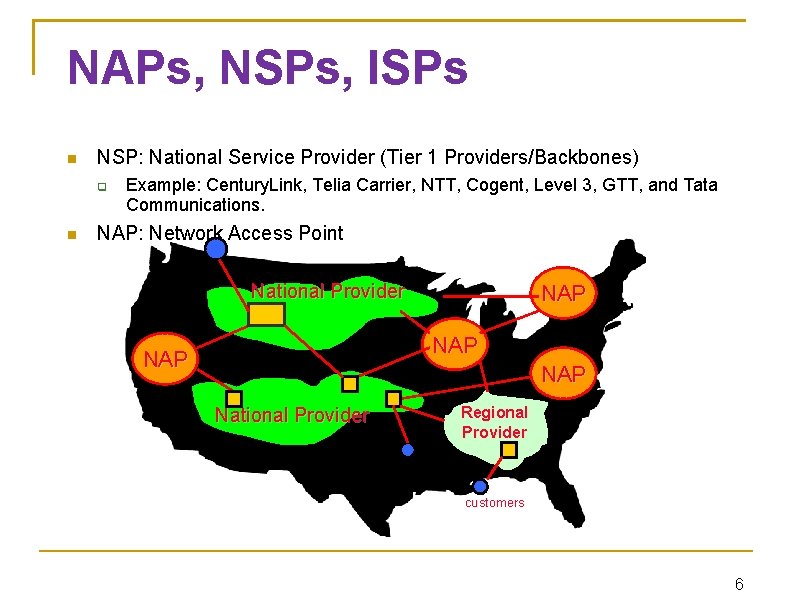
NAPs, NSPs, ISPs NSP: National Service Provider (Tier 1 Providers/Backbones) Example: Century. Link, Telia Carrier, NTT, Cogent, Level 3, GTT, and Tata Communications. NAP: Network Access Point National Provider NAP NAP National Provider Regional Provider customers 6

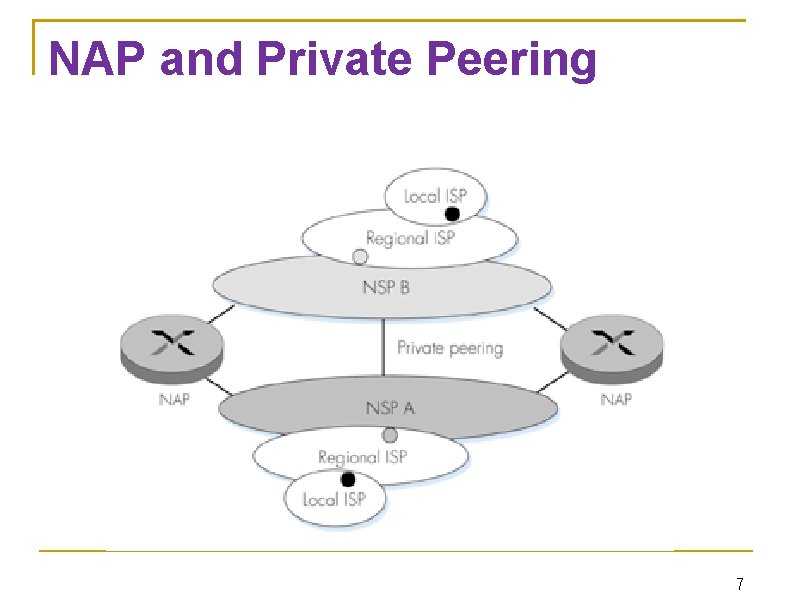
NAP and Private Peering 7

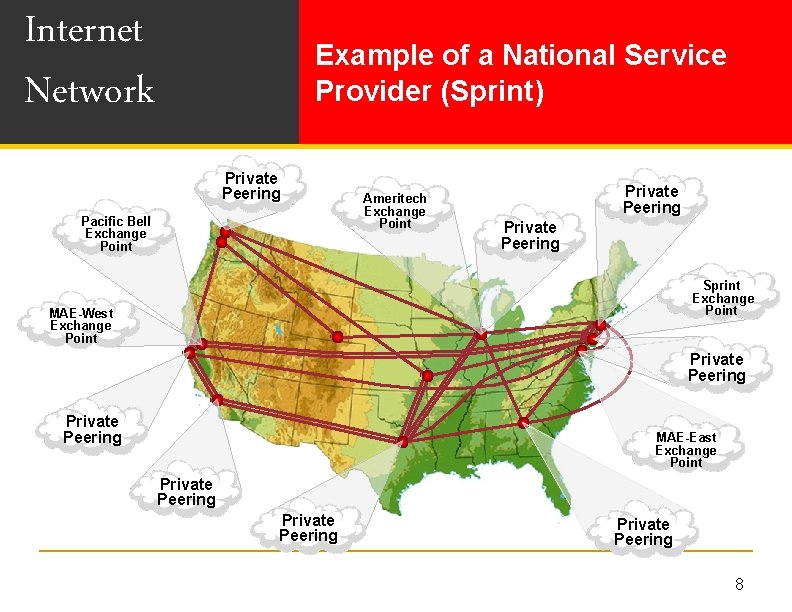
Internet Network Example of a National Service Provider (Sprint) Private Peering Pacific Bell Exchange Point Ameritech Exchange Point Private Peering Sprint Exchange Point MAE-West Exchange Point Private Peering MAE-East Exchange Point Private Peering 8

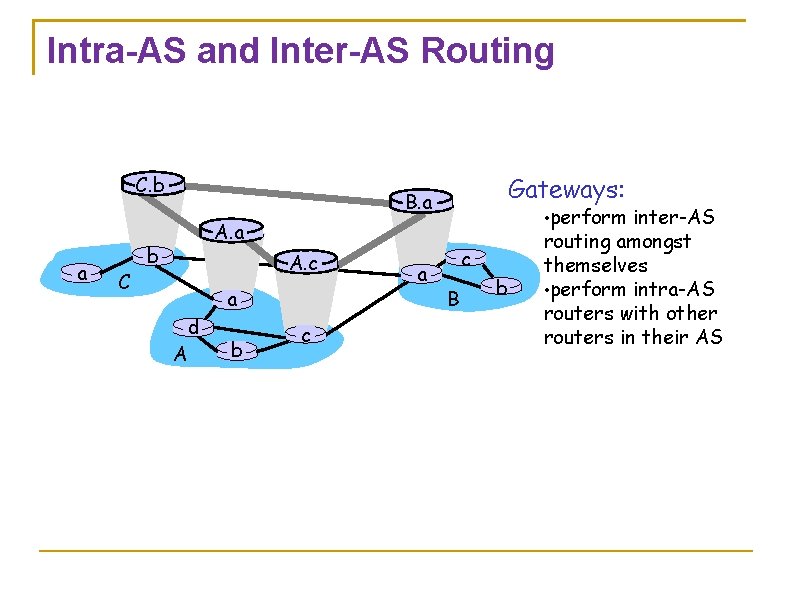
Intra-AS and Inter-AS Routing C. b a C Gateways: B. a • perform inter-AS A. a b A. c A d a b c a c B b routing amongst themselves • perform intra-AS routers with other routers in their AS

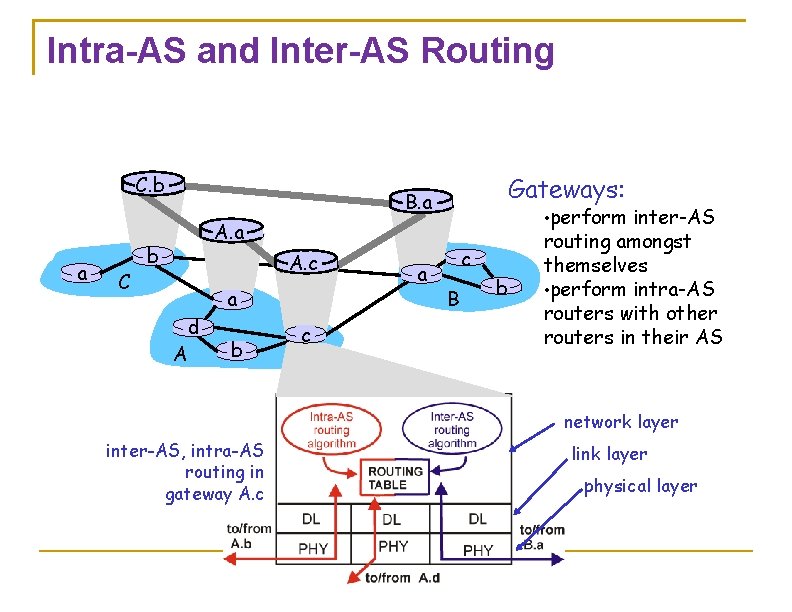
Intra-AS and Inter-AS Routing C. b a C Gateways: B. a • perform inter-AS A. a b A. c A d a b c a c B b routing amongst themselves • perform intra-AS routers with other routers in their AS network layer inter-AS, intra-AS routing in gateway A. c link layer physical layer

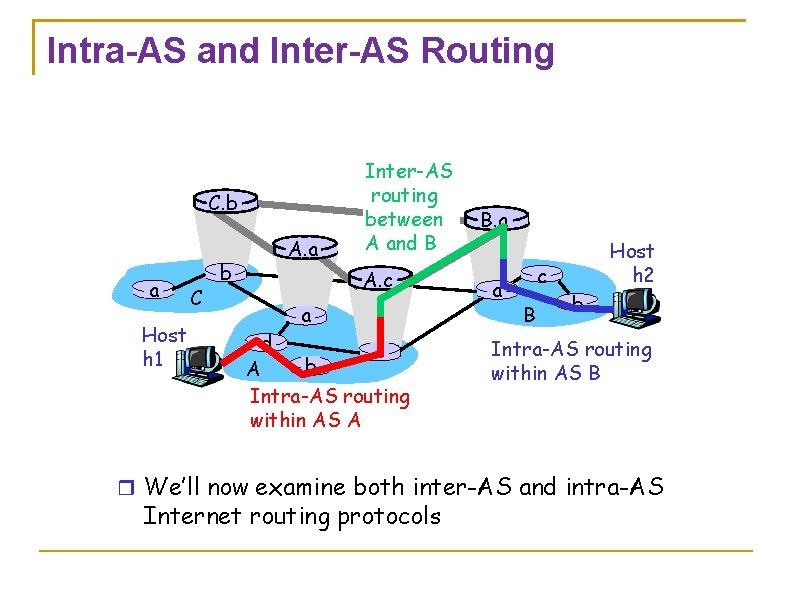
Intra-AS and Inter-AS Routing C. b a Host h 1 C A. a b Inter-AS routing between A and B A. c d a c b A Intra-AS routing within AS A B. a a Host h 2 c B b Intra-AS routing within AS B We’ll now examine both inter-AS and intra-AS Internet routing protocols

Intra-AS Routing a. k. a. , “routing in the small” These routing algorithms only scale for smaller networks (few hundred nodes), but set the stage for the hierarchical Inter-AS routing protocols used in the Internet today 12

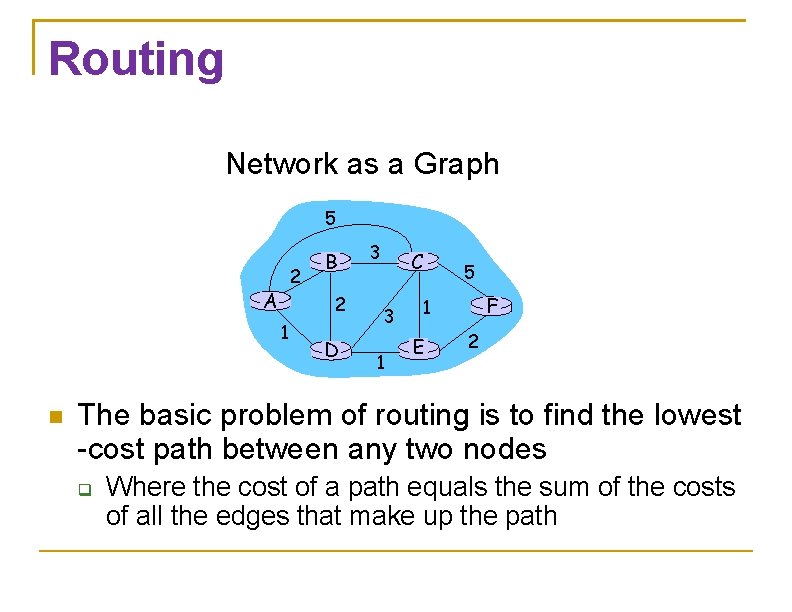
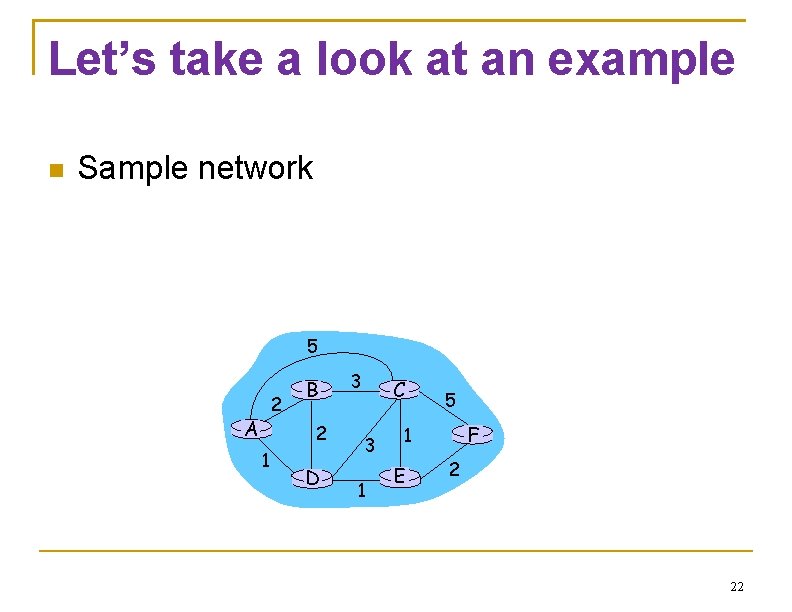
Routing Network as a Graph 5 2 A 2 1 B D 3 C 3 1 5 F 1 E 2 The basic problem of routing is to find the lowest -cost path between any two nodes Where the cost of a path equals the sum of the costs of all the edges that make up the path

Routing For a simple network, we can calculate all shortest paths and load them into some nonvolatile storage on each node. Such a static approach has several shortcomings It does not deal with node or link failures It does not consider the addition of new nodes or links It implies that edge costs cannot change

Routing Instead of a static approach, we need a dynamic way to find the lowest-cost path Node and link failures, changing link costs We would like these algorithms to be distributed so that they can be somewhat scalable 15

Distributed Routing Algorithms Routers cooperate using a distributed protocol To create mutually consistent routing tables Two standard distributed routing algorithms Link state routing Distance vector routing 16

Link State vs Distance Vector Both assume that Both find global information The address of each neighbor is known The cost of reaching each neighbor is known By exchanging routing info among neighbors Differ in info exchanged and route computation LS: tells every other node its distance to neighbors DV: tells neighbors its distance to every other node 17

Link State Algorithm Basic idea: Distribute to all routers Cost of each link in the network Each router independently computes optimal paths From itself to every destination Routes are guaranteed to be loop free if Each router sees the same cost for each link Uses the same algorithm to compute the best path 18

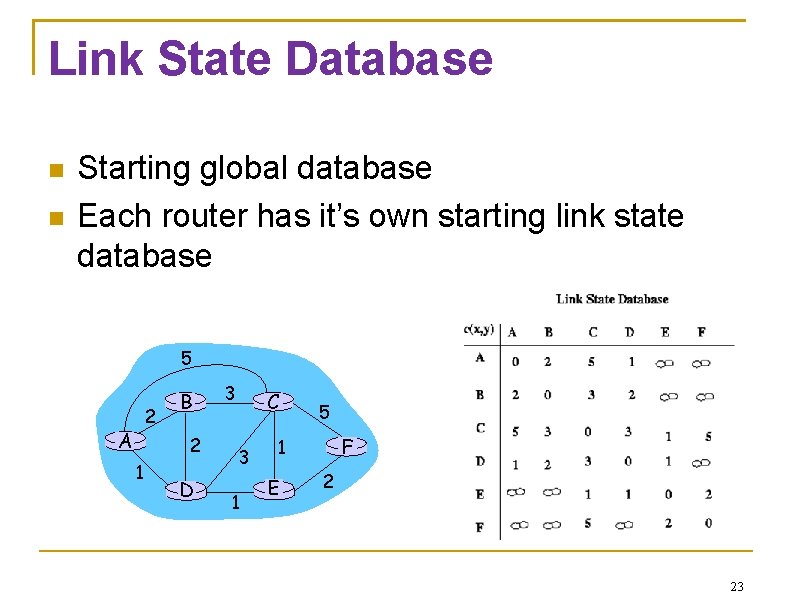
Topology Dissemination Each router creates a set of link state packets (LSPs) Describing its links to neighbors LSP contains Copies of LSPs are distributed to all routers Router id, neighbor’s id, and cost to its neighbor Using controlled flooding Each router maintains a topology database Database containing all LSPs 19

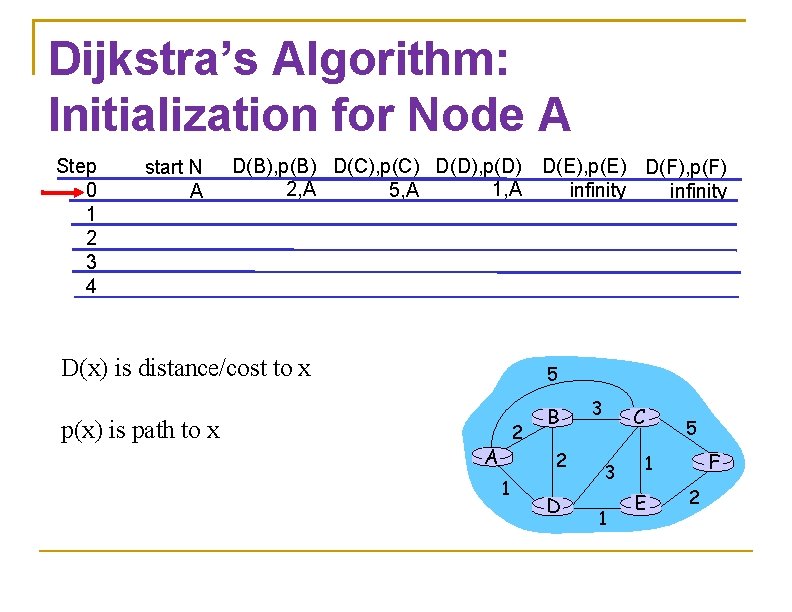
Dijkstra’s Algorithm Given the network topology How to compute shortest path to each destination? Some notation X: source node N: set of nodes to which shortest paths are known so far N is initially empty D(V): cost of known shortest path from source X from V C(U, V): cost of link U to V C(U, V) = if not neighbors 20

Algorithm (at Node X) Initialization N = {X} For all nodes V If V adjacent to X, D(V) = C(X, V) else D(V) = Loop Find U not in N such that D(U) is smallest Add U into set N Update D(V) for all V not in N D(V) = min{D(V), D(U) + C(U, V)} Until all nodes in N 21

Let’s take a look at an example Sample network 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2 22

Link State Database Starting global database Each router has it’s own starting link state database 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2 23

Dijkstra’s Algorithm: Initialization for Node A Step 0 1 2 3 4 start N A D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity D(x) is distance/cost to x p(x) is path to x 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

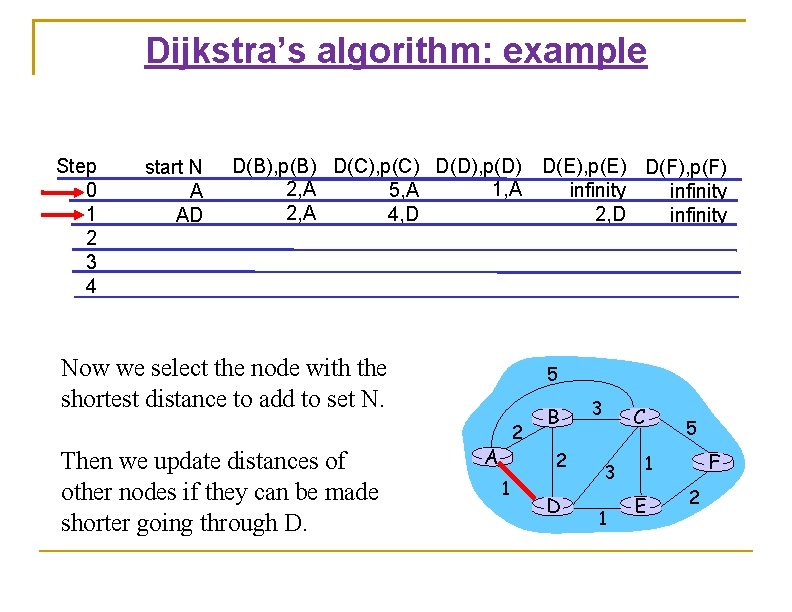
Dijkstra’s algorithm: example Step 0 1 2 3 4 start N A AD D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity 2, A 4, D 2, D infinity Now we select the node with the shortest distance to add to set N. Then we update distances of other nodes if they can be made shorter going through D. 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

Dijkstra’s algorithm: example Step 0 1 2 3 4 start N A AD ADB D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity 2, A 4, D 2, D infinity B has the next shortest distance from A, so we add it to set N. (could have been E. . ) Then we update distances of other nodes if they can be made shorter going through B… 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

Dijkstra’s algorithm: example Step 0 1 2 3 4 start N A AD ADBE D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity 2, A 4, D 2, D infinity 3, E 4, E 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

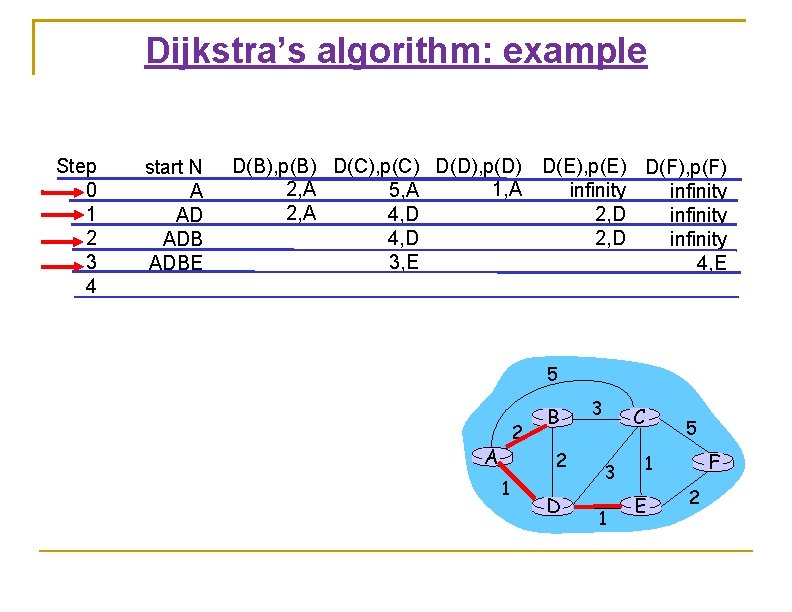
Dijkstra’s algorithm: example Step 0 1 2 3 4 start N A AD ADBEC D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity 2, A 4, D 2, D infinity 3, E 4, E 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

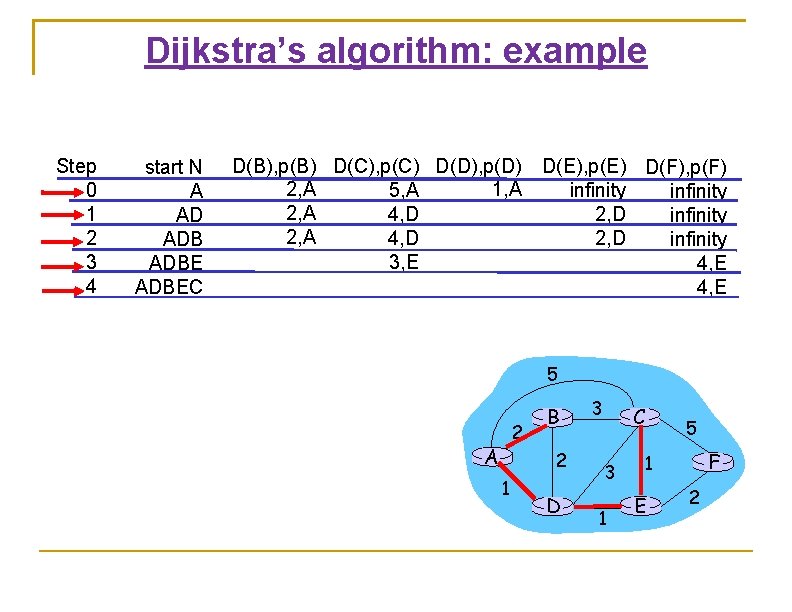
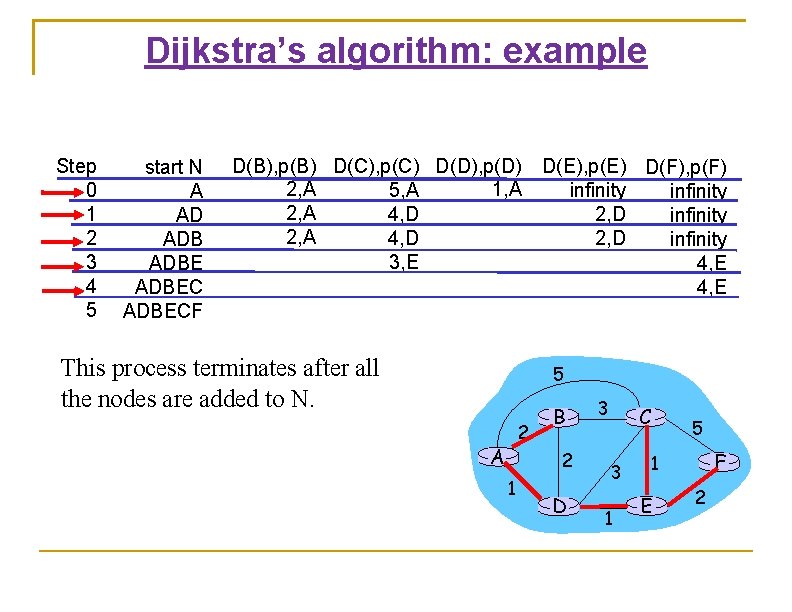
Dijkstra’s algorithm: example Step 0 1 2 3 4 5 start N A AD ADBECF D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity 2, A 4, D 2, D infinity 3, E 4, E This process terminates after all the nodes are added to N. 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

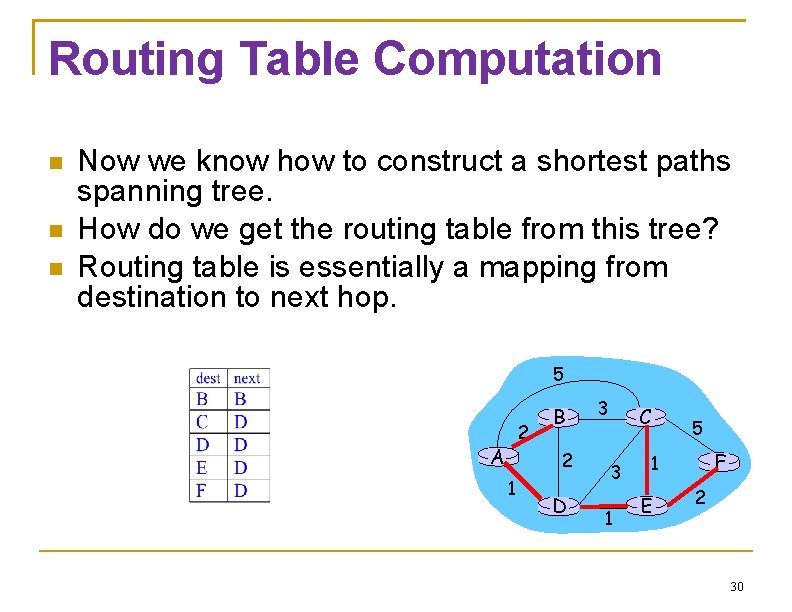
Routing Table Computation Now we know how to construct a shortest paths spanning tree. How do we get the routing table from this tree? Routing table is essentially a mapping from destination to next hop. 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2 30

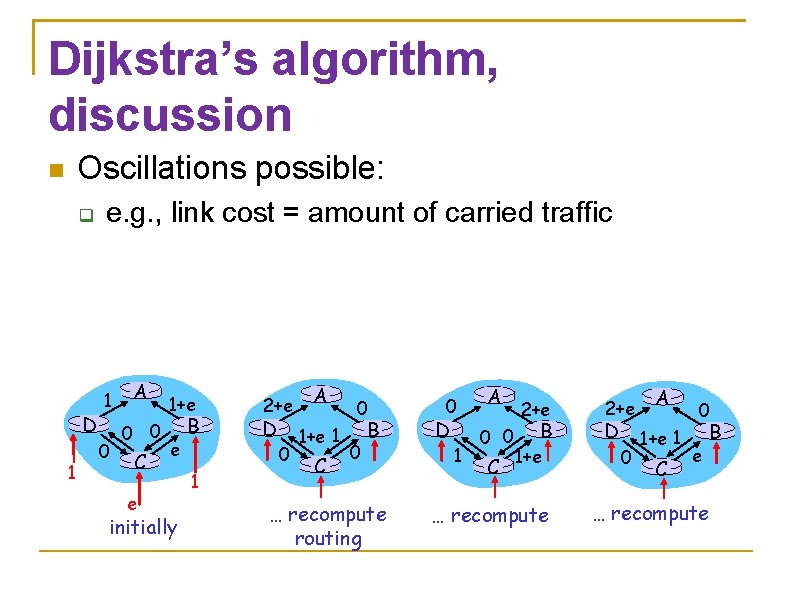
Dijkstra’s algorithm, discussion Oscillations possible: D 1 e. g. , link cost = amount of carried traffic 1 0 A 0 0 C e 1+e e initially B 1 2+e D 0 A 1+e 1 C 0 0 B … recompute routing 0 D 1 A 0 0 C 2+e B 1+e … recompute 2+e D 0 A 1+e 1 C 0 e B … recompute