Route Inspection Chinese Postman Problem Objectives 4 1

Route Inspection Chinese Postman Problem

Objectives 4. 1 Determine whether a graph is traversable 4. 2 Use the route inspection (Chinese postman algorithm to find the shortest inspection cycle in a network).

4. 1 Determine whether a graph is traversable e e r g de valency O f o r rde x e t r a ve The degree or valency or order of a vertex is the number of arcs incident to it.

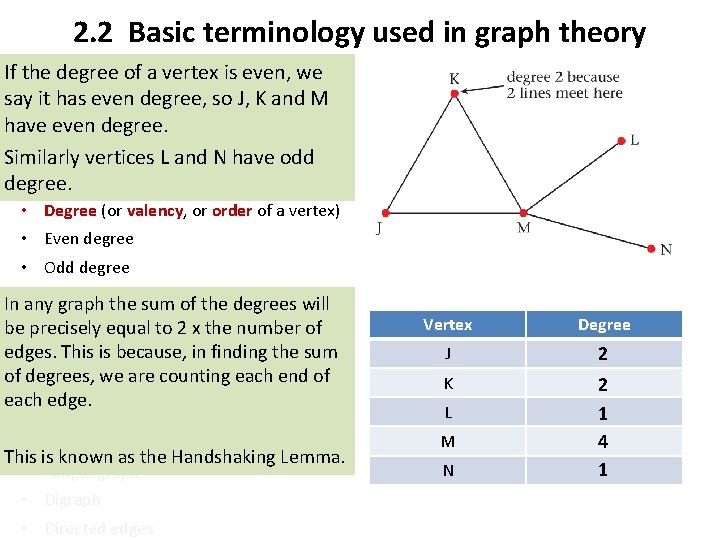
2. 2 Basic terminology used in graph theory (orof nodes) If • the. Vertices degree a vertex is even, we • it. Vertex set degree, so J, K and M say has even • Edges arcs) have even(or degree. • Edge set Similarly vertices L and N have odd • Subgraph degree. • Degree (or valency, or order of a vertex) • Even degree • Odd degree In • any. Path graph the sum of the degrees will Walk equal to 2 x the number of be • precisely edges. This(oriscircuit) because, in finding the sum • Cycle of • degrees, we are counting each end of connected each edge. Vertex Degree J 2 K 2 1 4 1 • Not connected L • loop M • Simple graph • Digraph N This is known as the Handshaking Lemma. • Directed edges

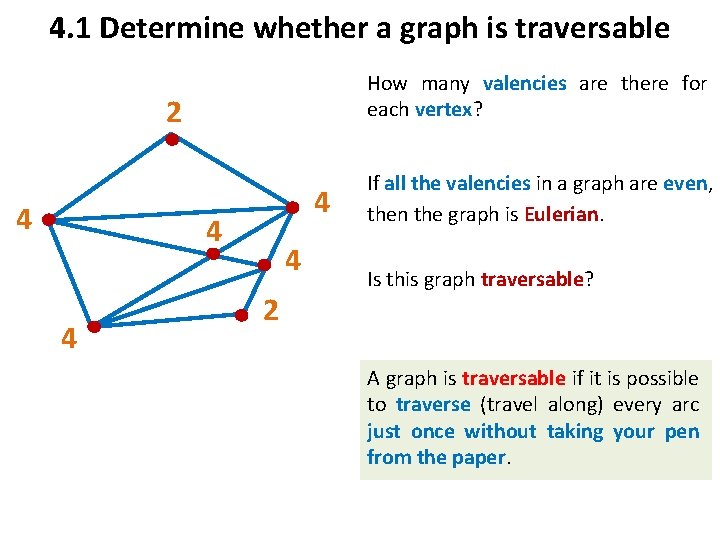
4. 1 Determine whether a graph is traversable How many valencies are there for each vertex? 2 4 4 4 2 If all the valencies in a graph are even, then the graph is Eulerian. Is this graph traversable? A graph is traversable if it is possible to traverse (travel along) every arc just once without taking your pen from the paper.

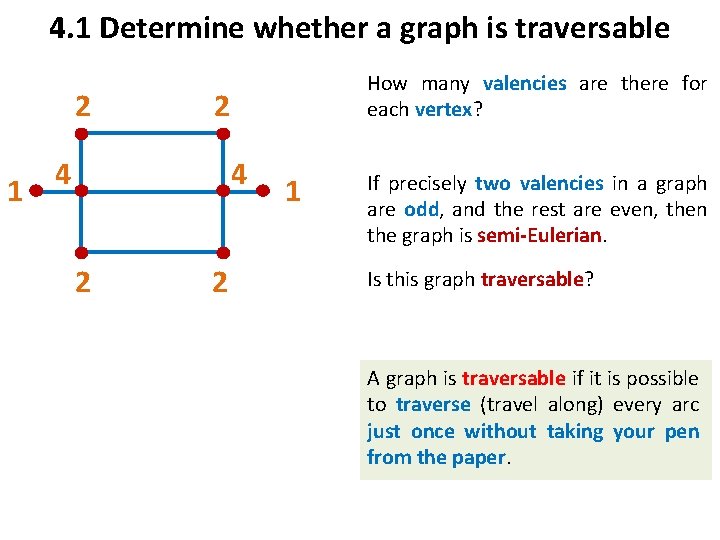
4. 1 Determine whether a graph is traversable 2 1 How many valencies are there for each vertex? 2 4 4 2 2 1 If precisely two valencies in a graph are odd, and the rest are even, then the graph is semi-Eulerian. Is this graph traversable? A graph is traversable if it is possible to traverse (travel along) every arc just once without taking your pen from the paper.

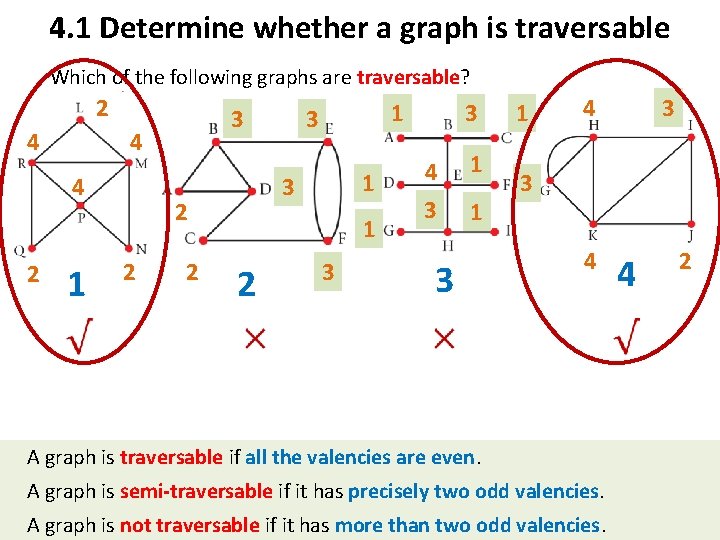
4. 1 Determine whether a graph is traversable Which of the following graphs are traversable? 2 4 4 4 2 3 1 2 1 3 2 2 1 3 1 2 3 3 4 1 3 1 4 3 3 4 A graph is traversable if all the valencies are even. A graph is semi-traversable if it has precisely two odd valencies. A graph is not traversable if it has more than two odd valencies. 4 2

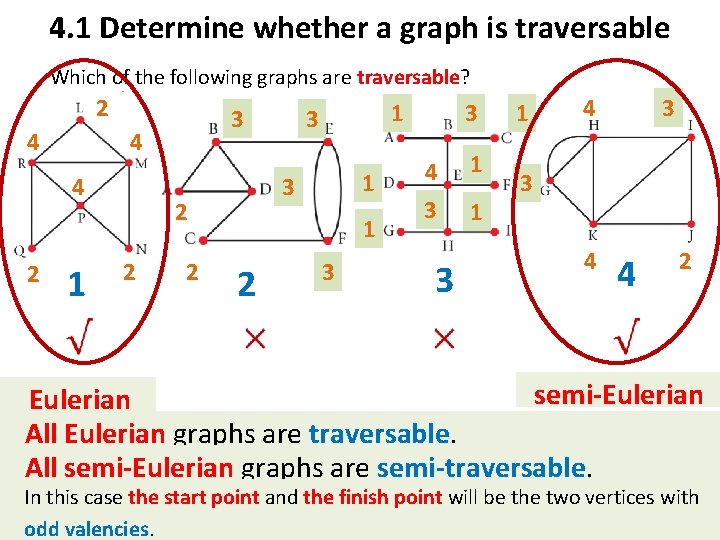
4. 1 Determine whether a graph is traversable Which of the following graphs are traversable? 2 4 4 4 2 3 1 2 1 3 2 2 1 3 1 2 3 3 4 1 3 1 4 3 3 4 4 2 semi-Eulerian All Eulerian graphs are traversable. A graph is traversable if all the valencies are even. All semi-Eulerian graphs are semi-traversable. A graph is semi-traversable if itthe hasfinish precisely valencies. In this case the start point and pointtwo willodd be the two vertices with A graph is not traversable if it has more than two odd valencies.

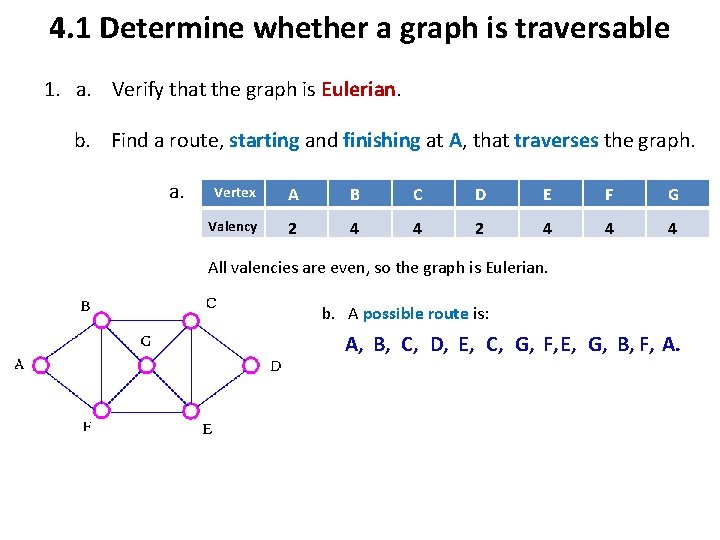
4. 1 Determine whether a graph is traversable 1. a. Verify that the graph is Eulerian. b. Find a route, starting and finishing at A, that traverses the graph. a. Vertex A B C D E F G Valency 2 4 4 4 All valencies are even, so the graph is Eulerian. b. A possible route is: A, B, C, D, E, C, G, F, E, G, B, F, A.

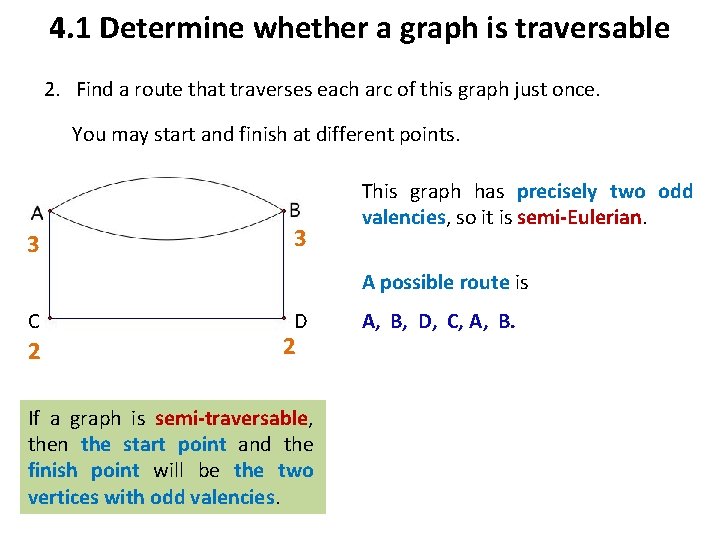
4. 1 Determine whether a graph is traversable 2. Find a route that traverses each arc of this graph just once. You may start and finish at different points. 3 3 This graph has precisely two odd valencies, so it is semi-Eulerian. A possible route is C 2 D 2 If a graph is semi-traversable, then the start point and the finish point will be the two vertices with odd valencies. A, B, D, C, A, B.

4. 1 Determine whether a graph is traversable 3. Prove that there must always be an even (or zero) number of vertices with odd valency in every graph.

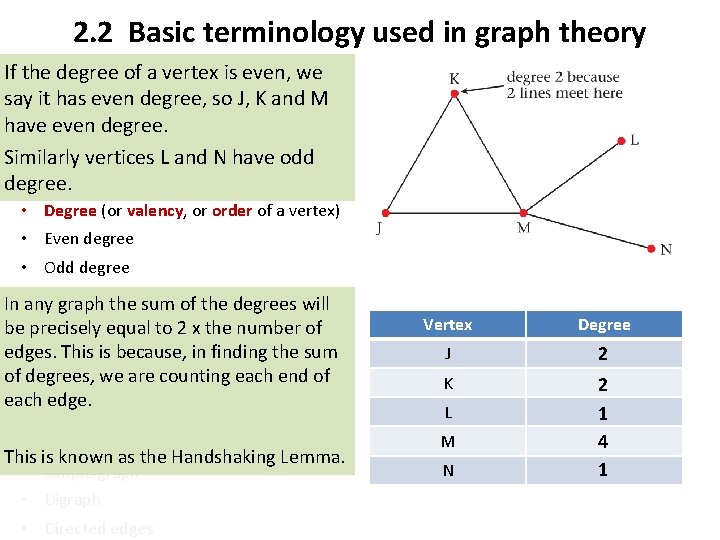
2. 2 Basic terminology used in graph theory (orof nodes) If • the. Vertices degree a vertex is even, we • it. Vertex set degree, so J, K and M say has even • Edges arcs) have even(or degree. • Edge set Similarly vertices L and N have odd • Subgraph degree. • Degree (or valency, or order of a vertex) • Even degree • Odd degree In • any. Path graph the sum of the degrees will Walk equal to 2 x the number of be • precisely edges. This(oriscircuit) because, in finding the sum • Cycle of • degrees, we are counting each end of connected each edge. Vertex Degree J 2 K 2 1 4 1 • Not connected L • loop M • Simple graph • Digraph N This is known as the Handshaking Lemma. • Directed edges

4. 1 Determine whether a graph is traversable 3. Prove that there must always be an even (or zero) number of vertices with odd valency in every graph. Each arc has two ends and so will contribute two to the sum of the valencies of the whole graph. The sum of the valencies = Number of arcs × 2 The sum of the valencies is even. Any odd numbers must occur in pairs. There is an even number of odd valencies.