Rounding Rules Scientific Notation Conversions Measuring Accuracy Precision

Rounding Rules, Scientific Notation, Conversions, Measuring, Accuracy & Precision, Graphing CHEMISTRY UNIT 1

Rounding Target: I can properly round to the hundredths place (this is the decimal place to which we will round when applicable. ) q. Rules q 1: If the digit in the thousandths place (. xxx) is a 0, 1, 2, 3 or 4, drop this digit and leave the remaining number unchanged (round it down). q. Ex: 1. 864 becomes 1. 86 q 2: If the digit in the thousandths place (. xxx) is a 5, 6, 7, 8 or 9, drop this digit and add 1 to the preceding digit (round it up). q. Ex: 1. 247 becomes 1. 25

Scientific Notation Targets: I can interpret numbers in both standard and scientific notation and can alternate between them. I can use my calculator to perform calculations using scientific notation. 602, 000, 000, 000 (standard notation) is the same as 6. 02 x 1023 (scientific notation) To change a number in standard notation to scientific notation, all we have to do is move the decimal left or right following these rules…

Scientific Notation Rules q 1: The decimal moves to the immediate right of the first non-zero number 9 and 6 3 and 7 q Ex: 374, 000: between the _____; 0. 000000965: between the ______ q 2: The direction of movement determines the sign (+ or -) q The decimal of a very large number in standard notation will move left q. This is considered + and no sign is written with the exponent q Ex: 374, 000; the decimal moves to the left until between the 3 and 7 q The decimal of a very small number in standard notation will move right q. This is considered – and this sign must be used with the exponent q Ex: 0. 000000965; the decimal moves to the right until between the 9 and 6 q 3: The number of times the decimal is moved determines the power of the exponent 7 times 8 times; 0. 000000965 is moved ___ q Ex: 374, 000 is moved ___

Scientific Notation Practice (no calculators) How would 374, 000 be written in scientific notation? 3. 74 x 108 How would 0. 000000965 be written in scientific notation? 9. 65 x 10 -7 How would 9. 57462358 x 1015 be written in standard notation? 9, 574, 623, 580, 000 How would 1. 2798 x 10 -18 be written in standard notation? . 00000000012798

Using Scientific Notation on a Calculator You can type in, for example, 6. 02 x 10^23 You can use the EE button above the _____ button (use 2 nd key as needed) 6. 02 E 23

Conversions Targets: I can set up an equality I can use my equalities to convert units; I can correctly convert units q We will need to convert from unit to unit often. To do this we will need to know how the units are related to each other. This is called an equality. q We also need to know what the prefixes mean: milli = 1/1000 centi = 1/100 kilo = 1000

Conversion Equalities we need to know q 1 kilo = 1000 base units q 1 base unit = 100 centiq 1 base unit = 1000 milliq. For example: q. For every 1 meter there are 100 centimeters q. For every 1 liter there are 1000 milliliters q. If going between centi and kilo: 100 x 1000 q. If going between milli and kilo: 1000 x 1000

Conversions q. To convert: q 1. Find the equality q 2. Set up proportions q 3. Solve by cross-multiplying and dividing

Conversion Practice and Setup Convert 200 cm to meters 100 cm = 1 m 200 cm Xm 100 cm = 1 m Now cross multiply: 200 cm x 1 m 100 cm x X m 200 cm x 1 m = 100 cm x X m Solve for X: (200 cm)(1 m) = X m 100 cm 2 m=Xm

Conversion Equality Setup Assistance You can also plug your values into this equation if you are having a hard time visualizing the equality/proportion. What you know from the data given in the problem (with units*) That for which you are trying to solve (with units**) Equality of the same unit** Note: since these are equalities (and essentially each side of the equal sign) has a value of 1, you can switch sides of the equation and which values are top and bottom BUT BE SURE TO KEEP EQUITABLE UNITS TOGETHER ON EITHER THE TOP OR THE BOTTOM

Conversion and Decimal Movement q You can also move the decimal according to the number of zeros in the conversion. Remember you always need more of something smaller to equal less of something bigger! For example: If you want to convert 3 meters to millimeters: there are 3 zeros in milli- so your decimal will move 3 times. You need to have more milli- to equal a base unit (meter) so your 3 meters will be equal to 3, 000 mm. If you want to convert 3 meters to kilometers: there are 3 zeros in kilo- so your decimal will move 3 times. You need to have less kilo- to equal a base unit (meter) so your 3 meters will be equal to. 003 km.

Measurement and Significant Digits Targets: I know which is the appropriate piece of lab equipment to use for a specific measurement. I can use my lab equipment properly. Using my lab equipment, I can measure properly. (Go to what you know, estimate one more. ) Steps: 1. Notice the smallest value markings on your lab equipment (this will be the place value of your smallest certain number) 2. Estimate to one more place value (this will be your ONLY estimated number)

Measurement and Significant Digits q Significant Digits: all of the digits that are read directly (certain and from the specific markings on the instrumentation) and one estimated (uncertain) digit q The accuracy of the sample being measured depends on how small the markings are on the instrumentation device

Measurement Instrumentation

Answer: 1. What is the smallest place value being measured? 2. What is this sample’s measurement for the smallest place value (certain)? 3. What is the estimated digit place value? 4. What is this sample’s measurement for the estimated place value? What piece of measurement instrumentation is this ?

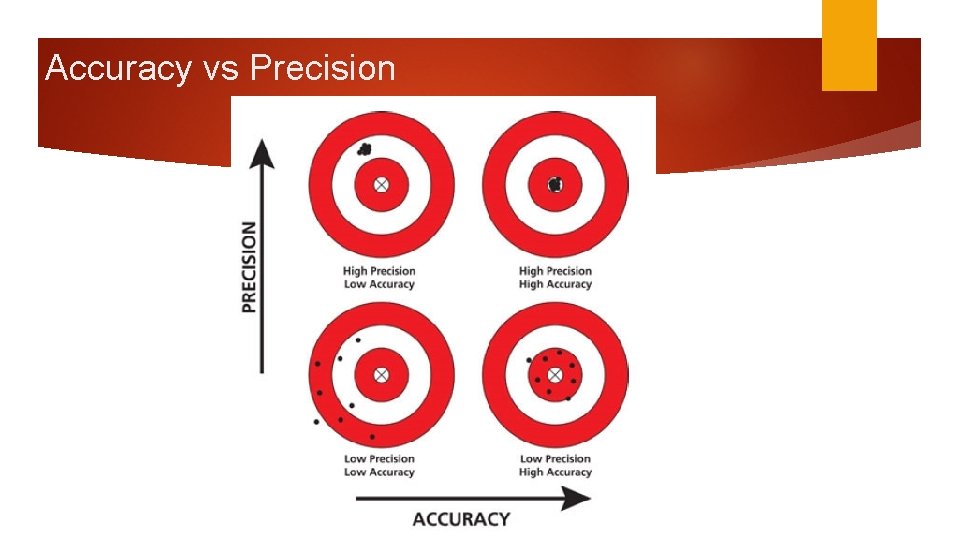
Accuracy and Precision Targets: I can differentiate between the terms “accurate” and “precise. ” I know which pieces of lab equipment are most and least accurate. When given a set of data, I can determine whether it is accurate, precise, both or neither. q Accuracy q How close you are to the accepted value q Precision q How close your data points are to each other

Accuracy vs Precision

Review and Practice 1. Read pages 62 through 67 2. Do Conceptual Problems 3. 1 on page 68 3. Read page 68 4. Do Sample Problems 3. 1 on on page 69 5. Read pages 70 and 71 and work through problems on each page

Graphing Targets: I know which is my X and which is my Y axis. I can identify my independent and dependent variables and know on which axis each belongs. I can make a proper scale for my graph. I can look at a graph and evaluate the meaning of the data provided. I can correctly create a line graph. I can determine a line of best fit (trend) given a set of data. I can calculate the slope of my line of best fit (trend). [rise/run]

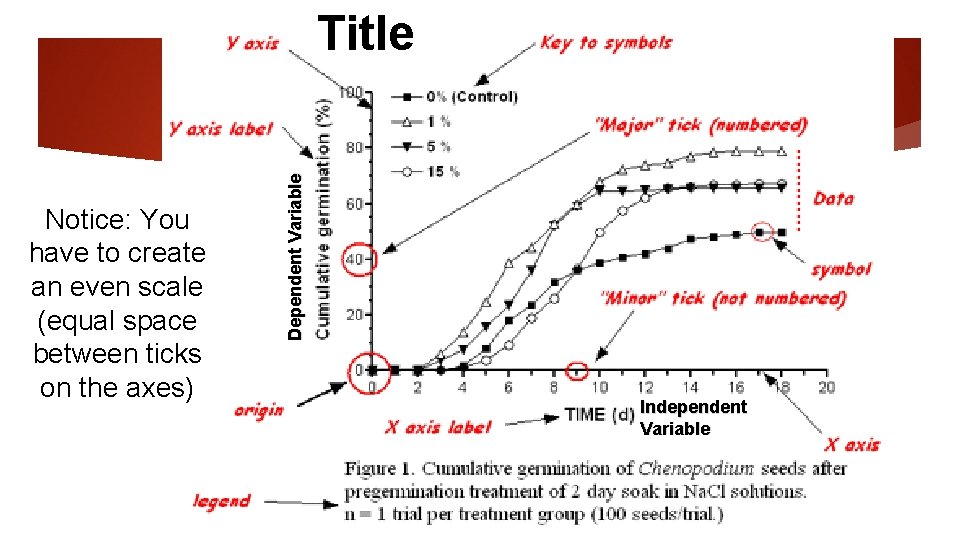
Notice: You have to create an even scale (equal space between ticks on the axes) Dependent Variable Title Independent Variable

Graphing q. The x axis q. Horizontal q. On the bottom q. Independent variable: what you change in your experiment q. The y axis q. Vertical q. On the side q. Dependent variable: what changes as a result of the independent variable

Graphing q. When setting up your graph always: q. Use proper scale q. Label each axis and include units q. Give the title in format “Dependent vs. Independent” q. Include a key if needed to explain multiple lines in the same graph

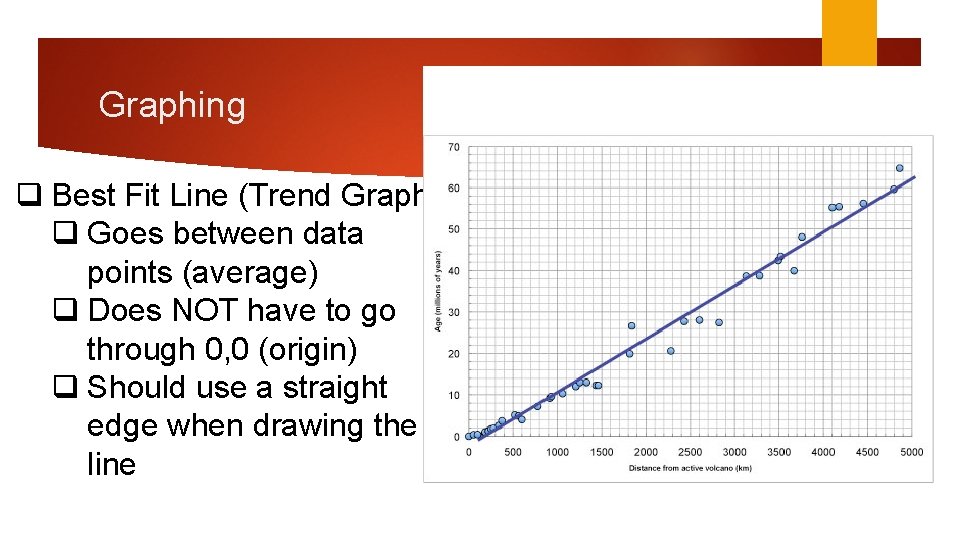
Graphing q Best Fit Line (Trend Graph) q Goes between data points (average) q Does NOT have to go through 0, 0 (origin) q Should use a straight edge when drawing the line

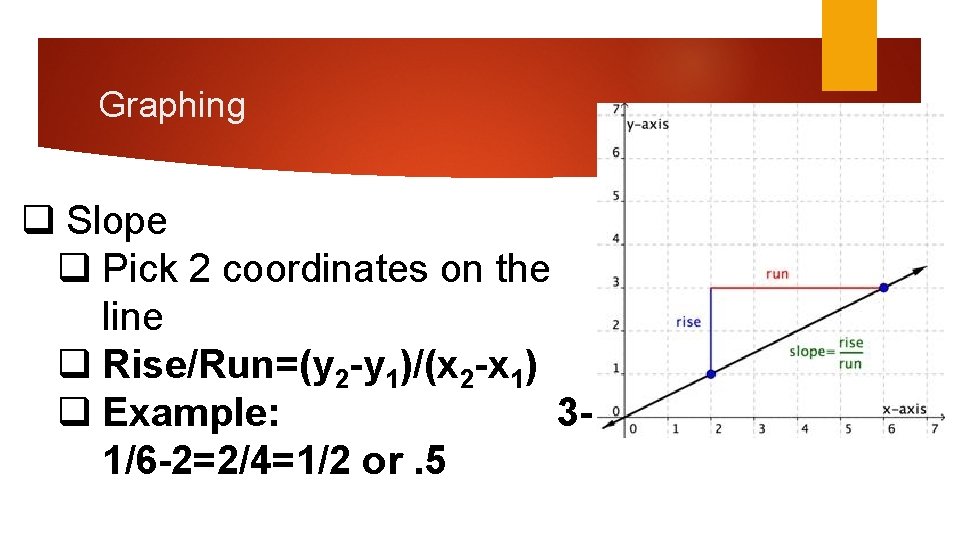
Graphing q Slope q Pick 2 coordinates on the line q Rise/Run=(y 2 -y 1)/(x 2 -x 1) q Example: 31/6 -2=2/4=1/2 or. 5