Rounding Decimal Places Demonstration This resource provides animated

Rounding – Decimal Places – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

The juice box says it contains 300 ml of juice. How much juice does the box contain? 300 ml It is unlikely the box contains exactly 300 ml. It may be more or less. Why do manufacturers want to be accurate? They don’t want to give you much juice for free, but they must legally have the amount stated.

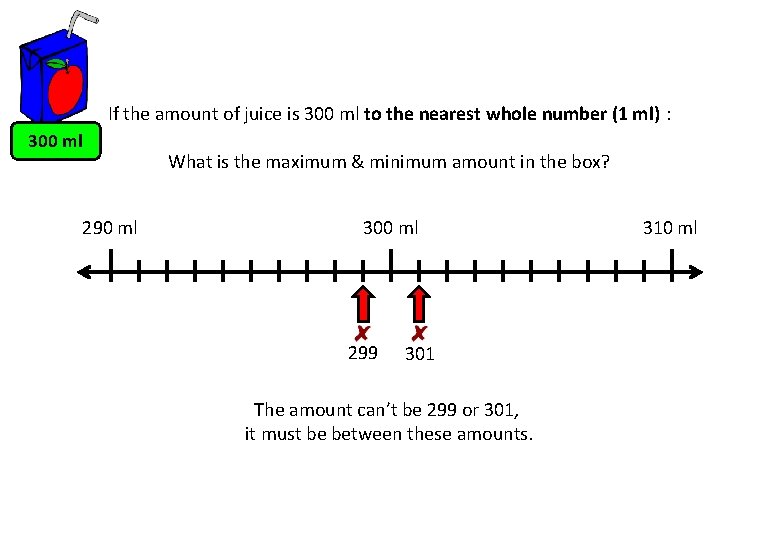
If the amount of juice is 300 ml to the nearest whole number (1 ml) : 300 ml 290 ml What is the maximum & minimum amount in the box? 300 ml 299 301 The amount can’t be 299 or 301, it must be between these amounts. 310 ml

If the amount of juice is 300 ml to the nearest whole number (1 ml) : 300 ml What is the maximum & minimum amount in the box? The real amount must be between 299. 5 & 300. 5 ml. All these values are closer to 300 than 299 or 301. 299 ml 299. 5 ml Closer to 299 300 ml 300. 5 ml 301 ml Closer to 301

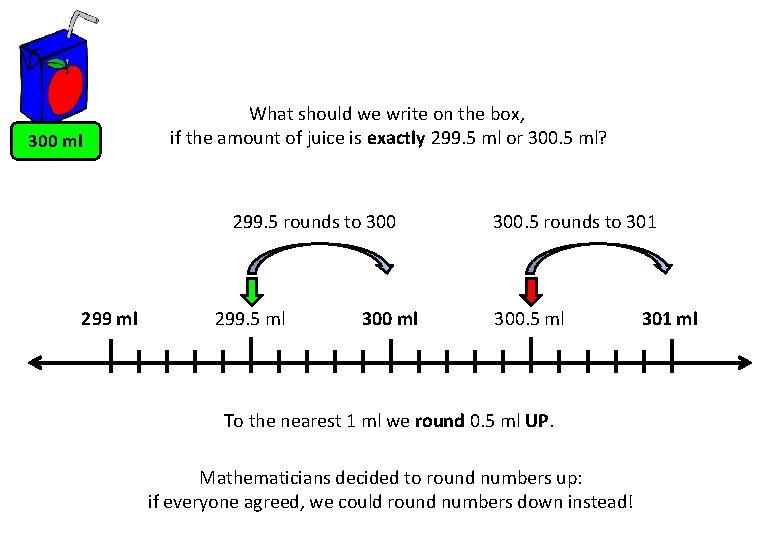
300 ml What should we write on the box, if the amount of juice is exactly 299. 5 ml or 300. 5 ml? 299. 5 rounds to 300 299 ml 299. 5 ml 300. 5 rounds to 301 300. 5 ml To the nearest 1 ml we round 0. 5 ml UP. Mathematicians decided to round numbers up: if everyone agreed, we could round numbers down instead! 301 ml

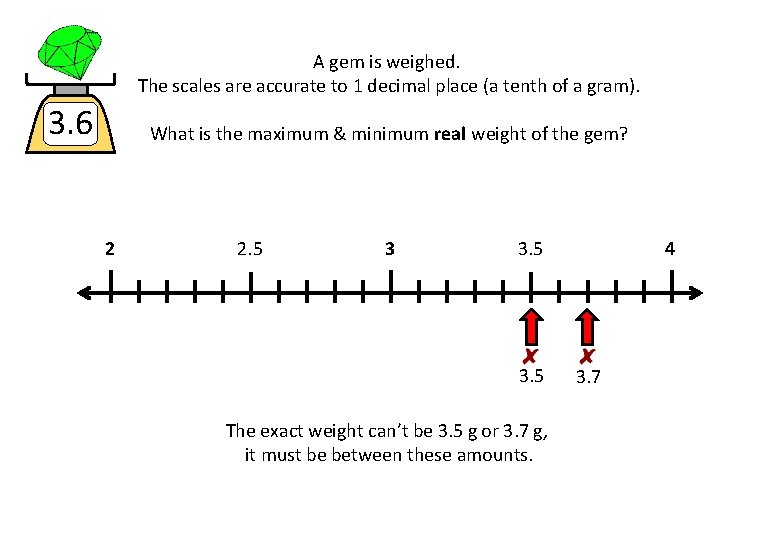
A gem is weighed. The scales are accurate to 1 decimal place (a tenth of a gram). 3. 6 What is the maximum & minimum real weight of the gem? 2 2. 5 3 3. 5 The exact weight can’t be 3. 5 g or 3. 7 g, it must be between these amounts. 4 3. 7

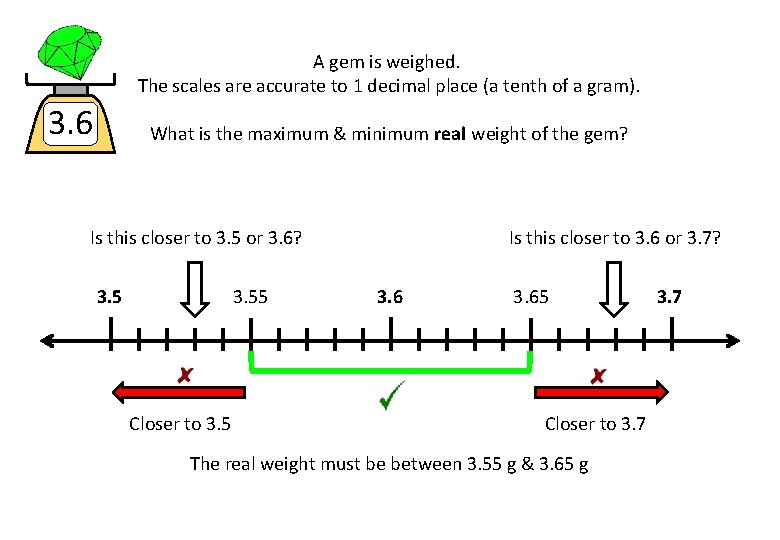
A gem is weighed. The scales are accurate to 1 decimal place (a tenth of a gram). 3. 6 What is the maximum & minimum real weight of the gem? Is this closer to 3. 5 or 3. 6? 3. 55 Closer to 3. 5 Is this closer to 3. 6 or 3. 7? 3. 65 Closer to 3. 7 The real weight must be between 3. 55 g & 3. 65 g 3. 7

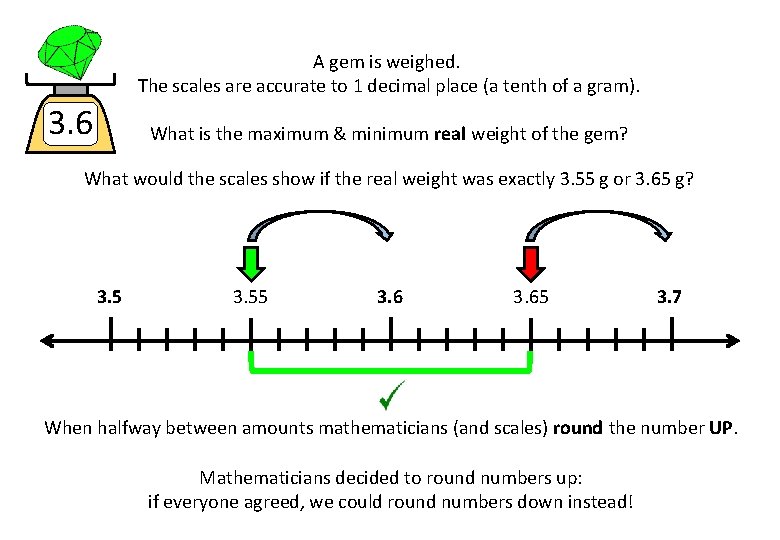
A gem is weighed. The scales are accurate to 1 decimal place (a tenth of a gram). 3. 6 What is the maximum & minimum real weight of the gem? What would the scales show if the real weight was exactly 3. 55 g or 3. 65 g? 3. 55 3. 65 3. 7 When halfway between amounts mathematicians (and scales) round the number UP. Mathematicians decided to round numbers up: if everyone agreed, we could round numbers down instead!

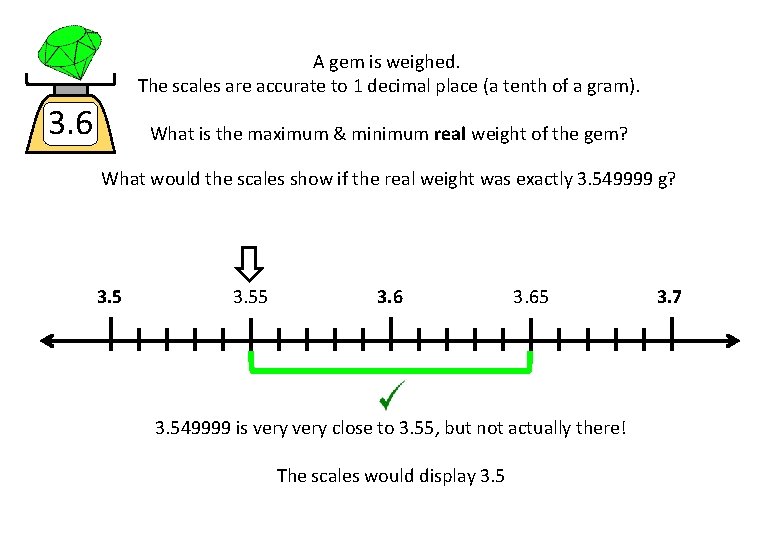
A gem is weighed. The scales are accurate to 1 decimal place (a tenth of a gram). 3. 6 What is the maximum & minimum real weight of the gem? What would the scales show if the real weight was exactly 3. 549999 g? 3. 55 3. 65 3. 549999 is very close to 3. 55, but not actually there! The scales would display 3. 5 3. 7

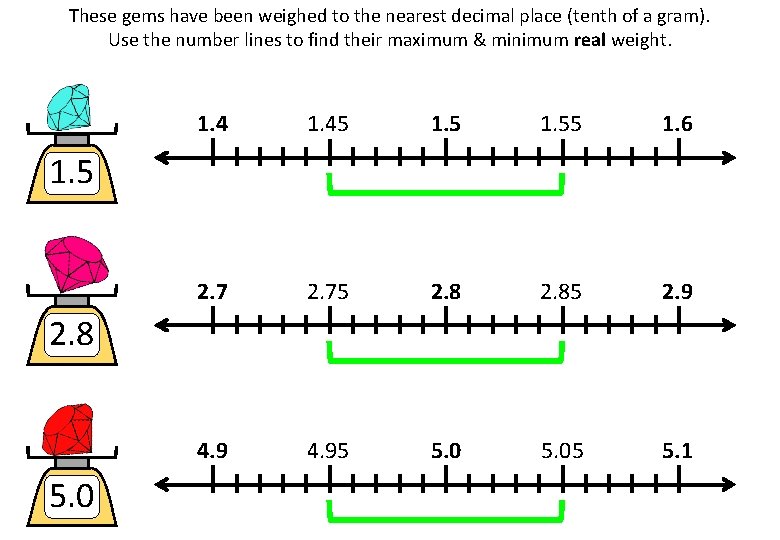
These gems have been weighed to the nearest decimal place (tenth of a gram). Use the number lines to find their maximum & minimum real weight. 1. 45 1. 55 1. 6 2. 75 2. 85 2. 9 4. 95 5. 05 5. 1 1. 5 2. 8 5. 0

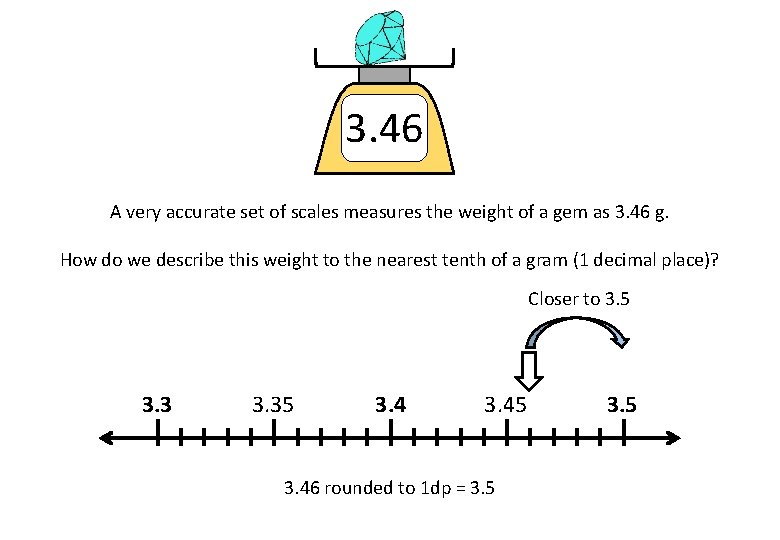
3. 46 A very accurate set of scales measures the weight of a gem as 3. 46 g. How do we describe this weight to the nearest tenth of a gram (1 decimal place)? Closer to 3. 5 3. 35 3. 45 3. 46 rounded to 1 dp = 3. 5

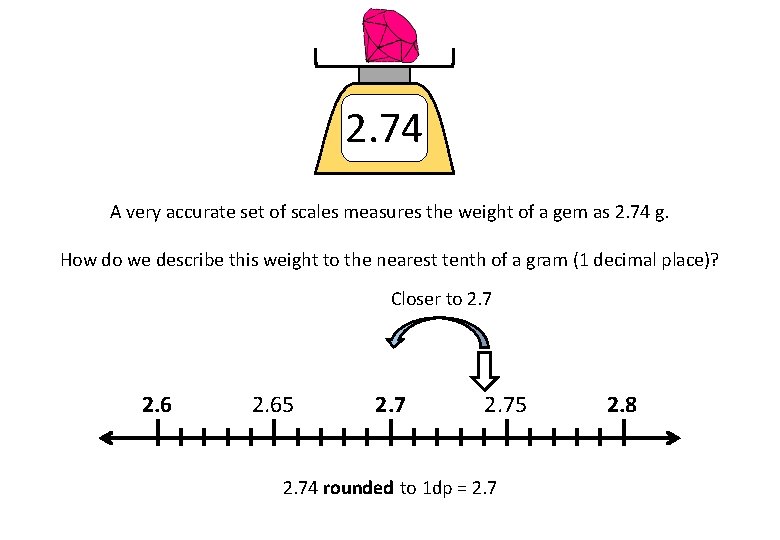
2. 74 A very accurate set of scales measures the weight of a gem as 2. 74 g. How do we describe this weight to the nearest tenth of a gram (1 decimal place)? Closer to 2. 7 2. 65 2. 75 2. 74 rounded to 1 dp = 2. 7 2. 8

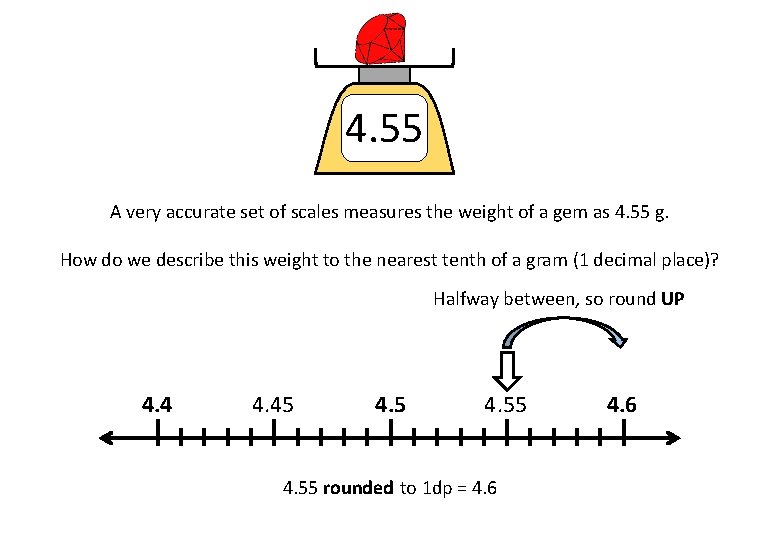
4. 55 A very accurate set of scales measures the weight of a gem as 4. 55 g. How do we describe this weight to the nearest tenth of a gram (1 decimal place)? Halfway between, so round UP 4. 45 4. 55 rounded to 1 dp = 4. 6

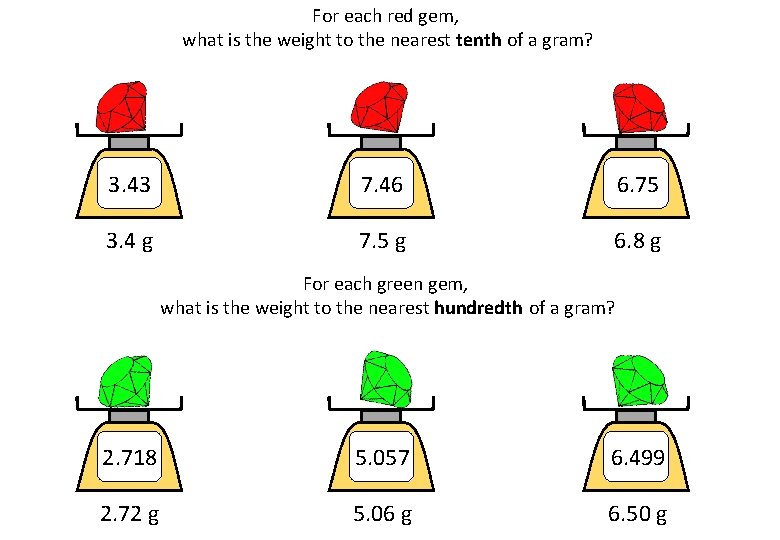
For each red gem, what is the weight to the nearest tenth of a gram? 3. 43 7. 46 6. 75 3. 4 g 7. 5 g 6. 8 g For each green gem, what is the weight to the nearest hundredth of a gram? 2. 718 5. 057 6. 499 2. 72 g 5. 06 g 6. 50 g

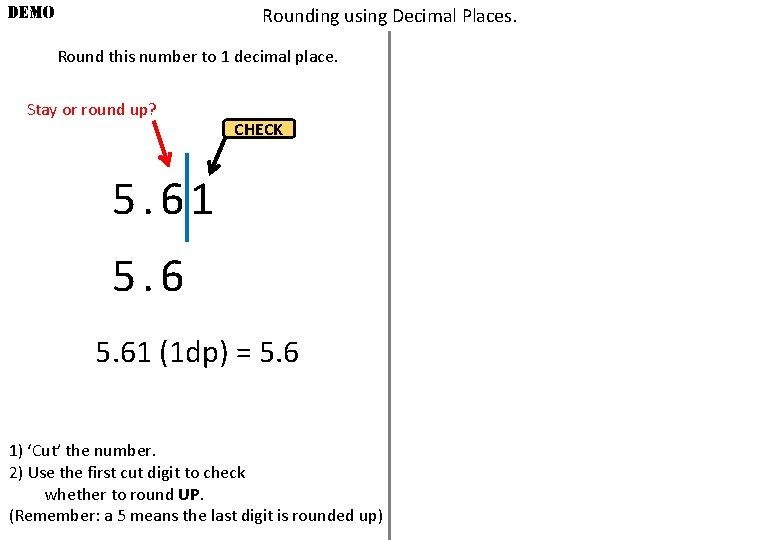
DEMO Rounding using Decimal Places. Round this number to 1 decimal place. Stay or round up? CHECK 5. 61 (1 dp) = 5. 6 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

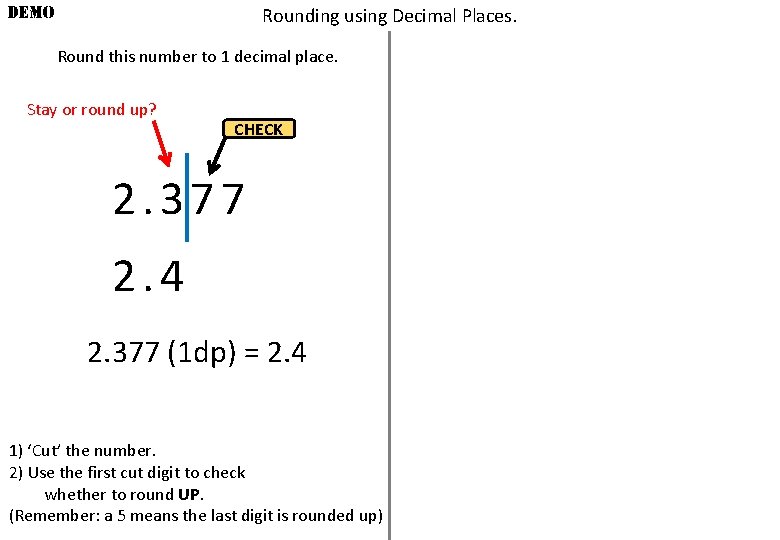
DEMO Rounding using Decimal Places. Round this number to 1 decimal place. Stay or round up? CHECK 2. 377 2. 4 2. 377 (1 dp) = 2. 4 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

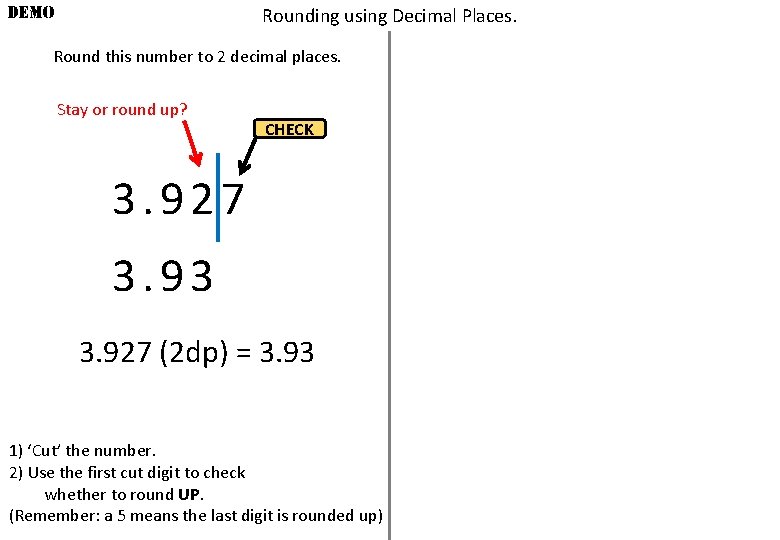
DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK 3. 927 3. 93 3. 927 (2 dp) = 3. 93 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

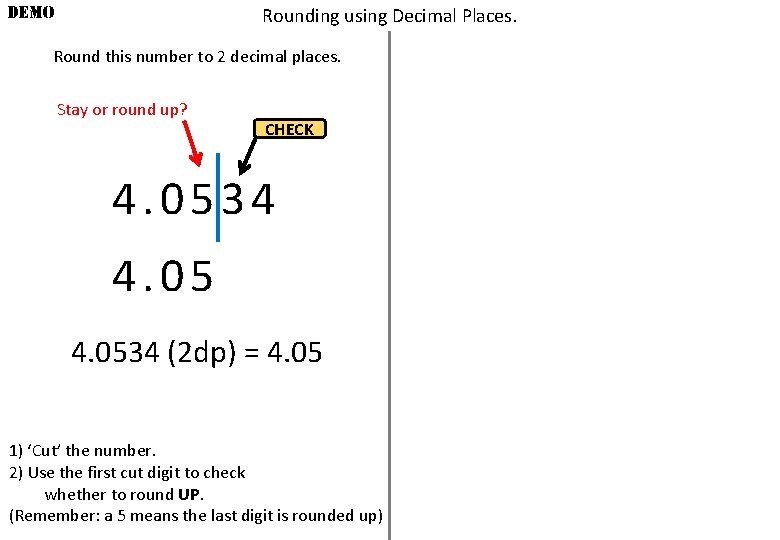
DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK 4. 0534 (2 dp) = 4. 05 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

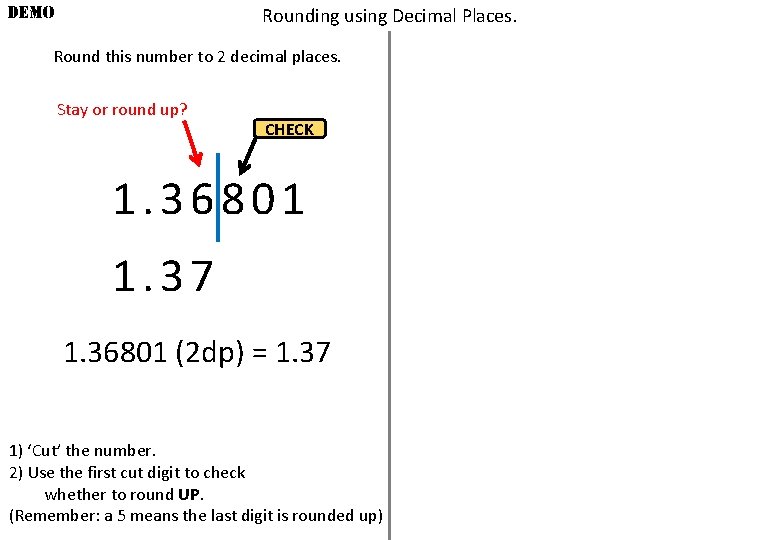
DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK 1. 36801 1. 37 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK 3. 5993 3. 60 3. 5993 (2 dp) = 3. 60 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

DEMO Rounding using Decimal Places. Round this number to 3 decimal places. Stay or round up? CHECK 7. 82148 (3 dp) = 7. 821 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

DEMO Rounding using Decimal Places. Round this number to 3 decimal places. Stay or round up? CHECK 0. 57994 0. 580 0. 57994 (3 dp) = 0. 580 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up)

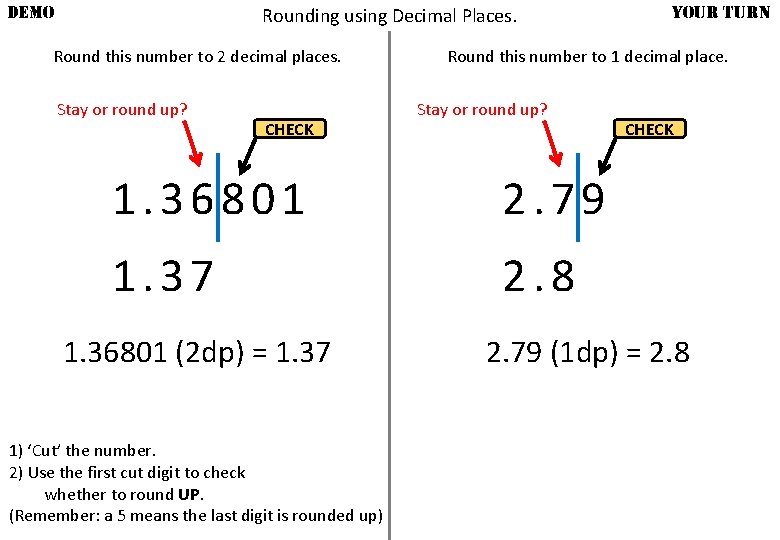
DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK Round this number to 1 decimal place. Stay or round up? 1. 36801 2. 79 1. 37 2. 8 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) YOUR TURN CHECK 2. 79 (1 dp) = 2. 8

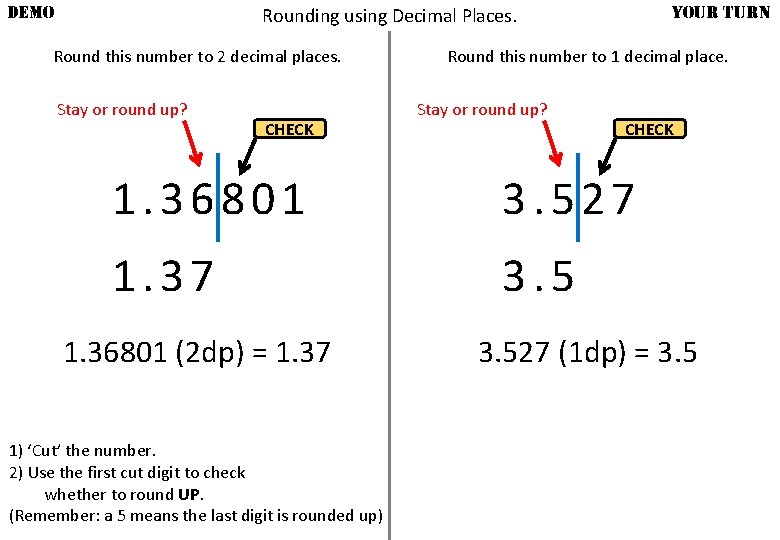
DEMO YOUR TURN Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK Round this number to 1 decimal place. Stay or round up? CHECK 1. 36801 3. 527 1. 37 3. 5 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) 3. 527 (1 dp) = 3. 5

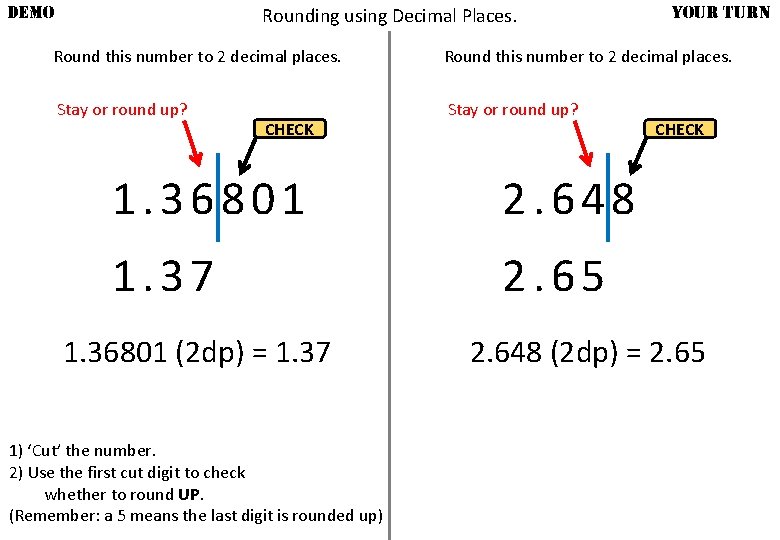
DEMO Rounding using Decimal Places. YOUR TURN Round this number to 2 decimal places. Stay or round up? CHECK 1. 36801 2. 648 1. 37 2. 65 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) CHECK 2. 648 (2 dp) = 2. 65

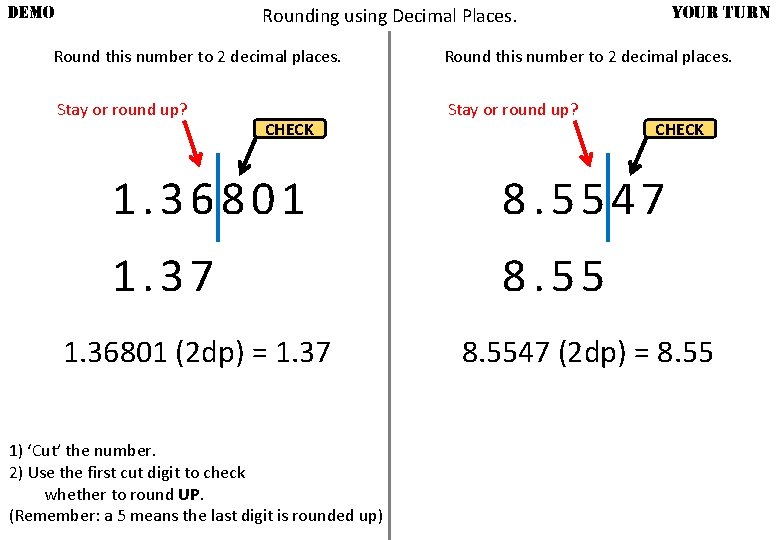
DEMO YOUR TURN Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK 1. 36801 8. 5547 1. 37 8. 55 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) 8. 5547 (2 dp) = 8. 55

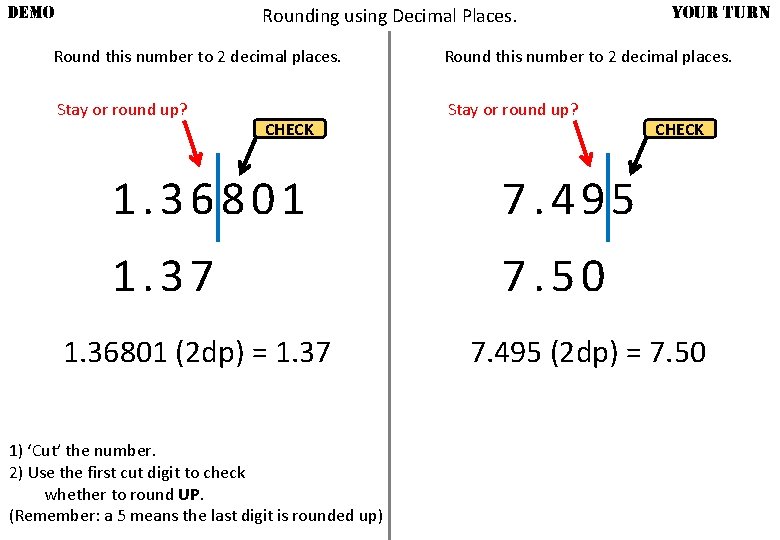
DEMO Rounding using Decimal Places. YOUR TURN Round this number to 2 decimal places. Stay or round up? CHECK 1. 36801 7. 495 1. 37 7. 50 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) CHECK 7. 495 (2 dp) = 7. 50

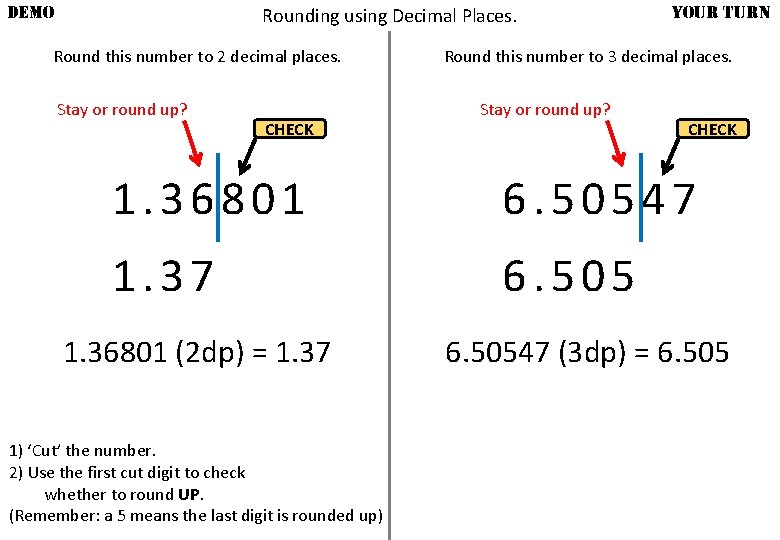
DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK YOUR TURN Round this number to 3 decimal places. Stay or round up? CHECK 1. 36801 6. 50547 1. 37 6. 505 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) 6. 50547 (3 dp) = 6. 505

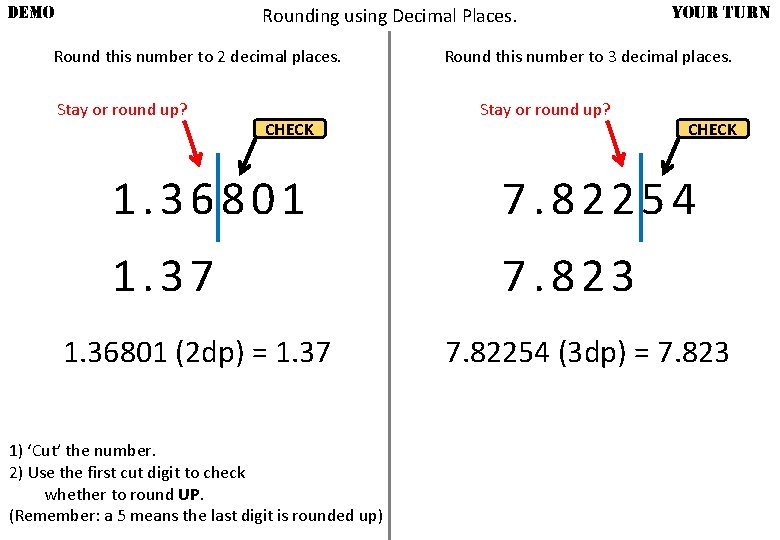
DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK YOUR TURN Round this number to 3 decimal places. Stay or round up? CHECK 1. 36801 7. 82254 1. 37 7. 823 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) 7. 82254 (3 dp) = 7. 823

DEMO Rounding using Decimal Places. Round this number to 2 decimal places. Stay or round up? CHECK YOUR TURN Round this number to 3 decimal places. Stay or round up? CHECK 1. 36801 5. 89962 1. 37 5. 900 1. 36801 (2 dp) = 1. 37 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) 5. 89962 (3 dp) = 5. 900

DEMO Rounding using decimal places. Round this number to 2 decimal places. Stay or round up? CHECK 1. 36801 1. 37 1. 36801 (2 dp) = 1. 37 YOUR TURN Round these numbers to 1 decimal place. a) 7. 83 (1 dp) = 7. 8 b) 4. 652 (1 dp) = 4. 7 c) 2. 9613 (1 dp) = 3. 0 Round these numbers to 2 decimal places. d) 0. 5492 (2 dp) = 0. 55 e) 7. 40622 (2 dp) = 7. 41 f) 9. 5934 (2 dp) = 9. 59 Round these numbers to 3 decimal places. 1) ‘Cut’ the number. 2) Use the first cut digit to check whether to round UP. (Remember: a 5 means the last digit is rounded up) g) 8. 22533 (3 dp) = 8. 225 h) 0. 56991 (3 dp) = 0. 570 i) 12. 6557 (3 dp) = 12. 656

2. 46 = 2. 5 What is wrong with what Joe wrote? 2. 46 is not exactly equal to 2. 5 2. 46 to approximately equal to 2. 5 2. 46 ≈ 2. 5 2. 46 (1 dp) = 2. 5 This is correct because we have stated how we have rounded the number.

Which is correct? 2. 503 (2 dp) = 2. 5 We keep the zero to keep its value & give extra information as to how the number was rounded.

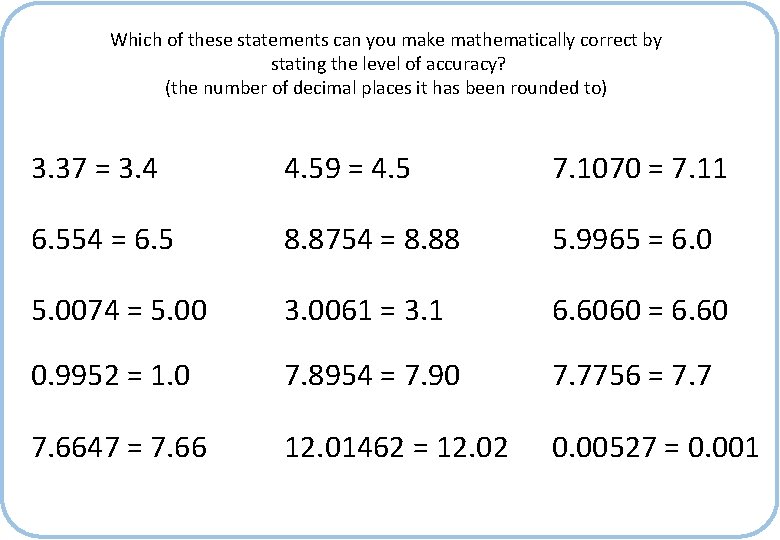
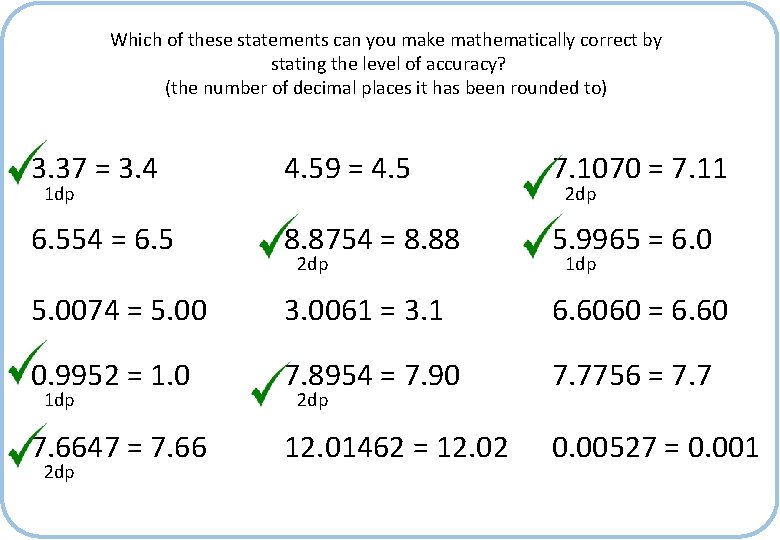
Which of these statements can you make mathematically correct by stating the level of accuracy? (the number of decimal places it has been rounded to) 3. 37 = 3. 4 4. 59 = 4. 5 7. 1070 = 7. 11 6. 554 = 6. 5 8. 8754 = 8. 88 5. 9965 = 6. 0 5. 0074 = 5. 00 3. 0061 = 3. 1 6. 6060 = 6. 60 0. 9952 = 1. 0 7. 8954 = 7. 90 7. 7756 = 7. 7 7. 6647 = 7. 66 12. 01462 = 12. 02 0. 00527 = 0. 001

Which of these statements can you make mathematically correct by stating the level of accuracy? (the number of decimal places it has been rounded to) 3. 37 = 3. 4 4. 59 = 4. 5 7. 1070 = 7. 11 6. 554 = 6. 5 8. 8754 = 8. 88 5. 9965 = 6. 0 5. 0074 = 5. 00 3. 0061 = 3. 1 6. 6060 = 6. 60 0. 9952 = 1. 0 7. 8954 = 7. 90 7. 7756 = 7. 7 7. 6647 = 7. 66 12. 01462 = 12. 02 0. 00527 = 0. 001 1 dp 2 dp 2 dp 1 dp

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk