Rough Set Model Selection for Practical Decision Making

Rough Set Model Selection for Practical Decision Making Jeseph P. Herbert Jing. Tao Yao Department of Computer Science University of Regina jtyao@cs. uregina. ca J T Yao Rough Set Model Selection for Practical Decision Making

Introduction • Rough sets have been applied to many areas in order to aid decision making. – Information (rules) derived from multiattribute data helps users in making decisions. – Rough set reducts minimize the strain on the user by giving them only the necessary information. J T Yao Rough Set Model Selection for Practical Decision Making 2

Motivation • Can we further utilize the strengths provided by rough sets in order to make more informed decisions? • Can we differentiate the types of decisions that can be made from using various rough set methods? • Can we provide some sort of support mechanism to the user to help them choose a suitable rough set method for their analysis? J T Yao Rough Set Model Selection for Practical Decision Making 3

Rough Sets • Developed in the early 1980 s by Zdzislaw Pawlak. • Sets derived from imperfect, imprecise, and incomplete data may not be able to be precisely defined. • Sets must be approximated – Using describable concepts to approximate known concept – 1. 76 cm => 1. 7, 1. 8 J T Yao Rough Set Model Selection for Practical Decision Making 4

Key Concepts • Information systems/tables and decision tables. • Indiscernibility. • Set approximation. • Reducts. J T Yao Rough Set Model Selection for Practical Decision Making 5

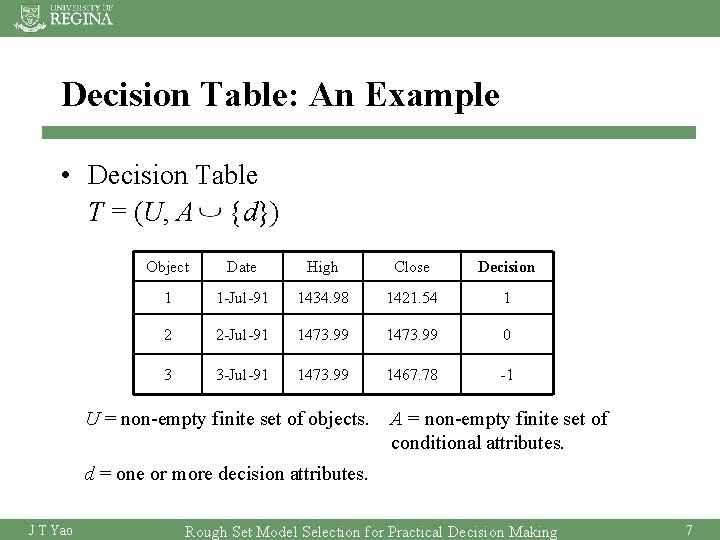
Information Table: An Example • Information table I = (U, A) • U = non-empty finite set of objects Object Date High Close 1 1 -Jul-91 1434. 98 1421. 54 2 2 -Jul-91 1473. 99 3 3 -Jul-91 1473. 99 1467. 78 • A = non-empty finite set of attributes such that: for all J T Yao is the set of value for attribute a. Rough Set Model Selection for Practical Decision Making 6

Decision Table: An Example • Decision Table T = (U, A {d}) Object Date High Close Decision 1 1 -Jul-91 1434. 98 1421. 54 1 2 2 -Jul-91 1473. 99 0 3 3 -Jul-91 1473. 99 1467. 78 -1 U = non-empty finite set of objects. A = non-empty finite set of conditional attributes. d = one or more decision attributes. J T Yao Rough Set Model Selection for Practical Decision Making 7

Indiscernibility • For any in I = ( an equivalence relation: where relation. ), there exists is the B-indiscernibility • An equivalence relation partitions U into equivalence classes: J T Yao Rough Set Model Selection for Practical Decision Making 8

Set Approximation • Data may not precisely define distinct, crisp sets. • A rough set has a lower and upper approximation. J T Yao Rough Set Model Selection for Practical Decision Making 9

Visualize Rough Sets Let T = (U, A), , • Lower Approximation: • Upper Approximation: • Boundary Region: J T Yao Rough Set Model Selection for Practical Decision Making 10

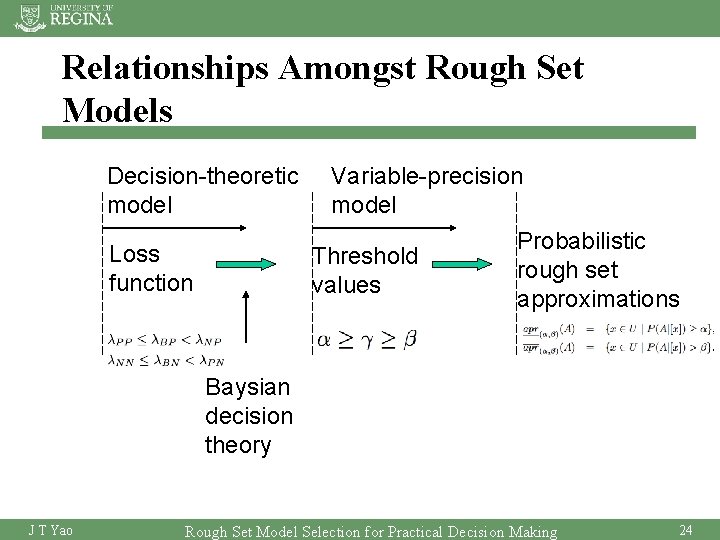
Rough Set Methods for Data Analysis • Two type of models are focused on: – Algebraic Method – Probabilistic • Decision-theoretic Method, • Variable-precision Method • Each method has different strengths that can be used to improve decision making J T Yao Rough Set Model Selection for Practical Decision Making 11

Types of Decisions • Broadly, there are two main types of decisions that can be made using rough set analysis. – Immediate decisions (Unambiguous). – Delayed decisions (Ambiguous). • We can further categorize decision types by looking at rough set method strengths. J T Yao Rough Set Model Selection for Practical Decision Making 12

Immediate Decisions • These types of decisions are based upon classification with the POS and NEG regions. • The user can interpret findings as: – Classification into POS regions can be considered a “yes” answer. – Classification into NEG regions can be considered a “no” answer J T Yao Rough Set Model Selection for Practical Decision Making 13

Delayed Decisions • These types of decisions are based on classification in the BND region. • A “wait-and-see” approach to decision making. • A decision-maker can decrease ambiguity with the following: – Obtain more information (more data). – A decreased tolerance for acceptable loss (decisiontheoretic) or user thresholds (variable-precision). J T Yao Rough Set Model Selection for Practical Decision Making 14

Algebraic Decisions • Decisions made from algebraic rough set analysis. – Immediate • If P(A|[x]) = 1, then x is in POS(A). • If P(A|[x]) = 0, then x is in NEG(A). – Delayed • If 0 < P(A|[x]) < 1, then x is in BND(A). J T Yao Rough Set Model Selection for Practical Decision Making 15

Variable-Precision Decisions • Decisions made from variable-precision rough set analysis. • User-defined thresholds u and l representing lower and upper bounds to define regions. – Pure Immediate decisions. – User-Accepted Immediate decisions. – User-Rejected Immediate decisions. – Delayed decisions. J T Yao Rough Set Model Selection for Practical Decision Making 16

Variable-Precision Decisions • Pure Immediate • If P(A|[x]) = 1, then x is in POS 1 (A). • If P(A|[x]) = 0, then x is in NEG 0 (A). • User-Accepted Immediate • If u ≤ P(A|[x]) < 1, then x is in POSu (A). • User-Rejected Immediate • If 0 < P(A|[x]) ≤ l, then x is in NEGl (A). • Delayed • If l < P(A|[x]) < u, then x is in BNDl, u (A). J T Yao Rough Set Model Selection for Practical Decision Making 17

Decision-Theoretic Decisions • Decisions made from decision-theoretic rough set analysis. • Calculated cost (risk) using Bayesian decision procedure provides minimum α, β values for region division. – – J T Yao Pure Immediate decisions. Accepted Loss Immediate decisions. Rejected Loss Immediate decisions. Delayed decisions. Rough Set Model Selection for Practical Decision Making 18

Decision-Theoretic Decisions • Pure Immediate • If P(A|[x]) = 1, then x is in POS 1 (A). • If P(A|[x]) = 0, then x is in NEG 0 (A). • Accepted Loss Immediate • If α ≤ P(A|[x]) < 1, then x is in POSα (A). • User-Rejected Immediate • If 0 < P(A|[x]) ≤ β, then x is in NEGβ (A). • Delayed • If β < P(A|[x]) < α, then x is in BNDα, β (A). J T Yao Rough Set Model Selection for Practical Decision Making 19

A Simple Example: Parking a Car • Set of states: – – : meeting will be over in less than 2 hours, : meeting will be over in more than 2 hours. • Set of actions: – – J T Yao : park the car on meter : park the car on parking lot Rough Set Model Selection for Practical Decision Making 20

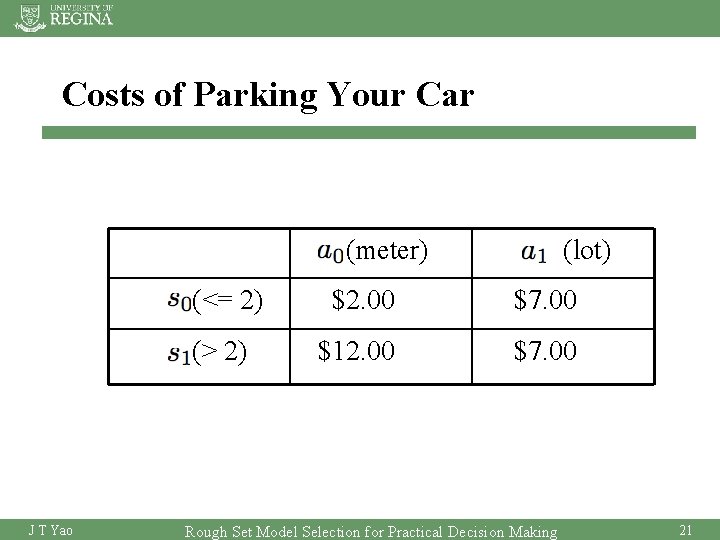
Costs of Parking Your Car (meter) J T Yao (lot) (<= 2) $2. 00 $7. 00 (> 2) $12. 00 $7. 00 Rough Set Model Selection for Practical Decision Making 21

Making Decision Based on Probabilities • Assume that: • Cost of each action: • Take action J T Yao : park the car on meter Rough Set Model Selection for Practical Decision Making 22

Determine the Probability Threshold for One Action • The condition of taking action car on meter: J T Yao : park the Rough Set Model Selection for Practical Decision Making 23

Relationships Amongst Rough Set Models Decision-theoretic model Loss function Variable-precision model Probabilistic Threshold rough set values approximations Baysian decision theory J T Yao Rough Set Model Selection for Practical Decision Making 24

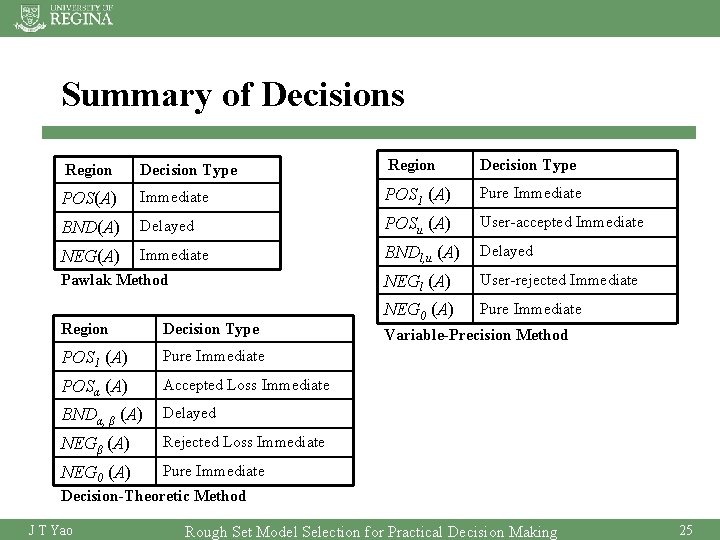
Summary of Decisions Region Decision Type POS(A) Immediate POS 1 (A) Pure Immediate BND(A) Delayed POSu (A) User-accepted Immediate NEG(A) Immediate BNDl, u (A) Delayed NEGl (A) User-rejected Immediate NEG 0 (A) Pure Immediate Pawlak Method Region Decision Type POS 1 (A) Pure Immediate POSα (A) Accepted Loss Immediate BNDα, β (A) Delayed NEGβ (A) Rejected Loss Immediate NEG 0 (A) Pure Immediate Variable-Precision Method Decision-Theoretic Method J T Yao Rough Set Model Selection for Practical Decision Making 25

Choosing a Method • If the user is informed enough to provide thresholds, variable-precision rough sets can be used for data analysis. • If cost or risk information is beneficial to the types of decisions being made, decisiontheoretic rough sets can be used for data analysis. J T Yao Rough Set Model Selection for Practical Decision Making 26

Conclusions • We can utilize the strengths of various rough set methods in order to improve our decision making capability. • The various rough set methods can each make different types of decisions. • By determining what kind of decisions they wish to make, users can choose a suitable rough set method for data analysis to reach their goals. J T Yao Rough Set Model Selection for Practical Decision Making 27

Rough Set Model Selection for Practical Decision Making Jeseph P. Herbert Jing. Tao Yao Department of Computer Science University of Regina jtyao@cs. uregina. ca J T Yao Rough Set Model Selection for Practical Decision Making

Where is Regina? J T Yao Rough Set Model Selection for Practical Decision Making 29