Roteiro para interpolar curvas de nvel Curva de

Roteiro para interpolar curvas de nível

Curva de nível pode ser definida como uma linha imaginária do terreno que une todos os pontos que tem a mesma altitude, acima ou abaixo do nível do mar. Interpolação: implica em determinar valores intermediários entre os valores conhecidos (pontos cotados). Após a determinação dos valores intermediários, deve-se unir as cotas de mesma altitude de maneira suavizada.

1) Verificar qual a eqüidistância pedida pelo exercício; 2) Verificar qual é a cota (valor da altitude) mais alta e a mais baixa;

3) Determinar a curva de nível mais alta e a mais baixa, conforme a eqüidistância solicitada ; (os valores devem sempre ser “redondos” ex. 10, 20, 30 no caso de eqüidistância de 10 em 10 m e nunca 22, 32, 42 ou 27, 37, 47);

4) Anotar o valor em metros das curvas de nível que deverão ser traçadas (as curvas de nível que passam entre a curva de nível mais alta e a mais baixa); Ex. : 250, 260, 270, 280, 290, 300, 310 e 320

5) Proceder a interpolação, obedecendo aos seguintes passos: 5. 1) descobrir onde se localiza a cota mais baixa. Escolher uma delas se houver duas iguais; 5. 2) verificar qual é o seu ponto cotado mais próximo (sem cruzar os rios);

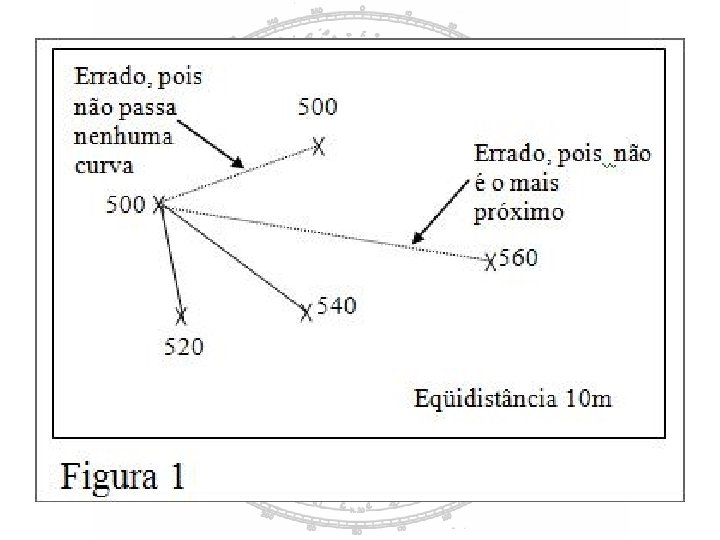
5. 3) checar se entre o ponto escolhido e o sua cota mais próxima passa alguma das curvas de nível anotadas no item 4;

5. 4) em caso positivo, unir as cotas com um traço à lápis (conforme figura 1) e calcular onde as curvas passam, usando a fórmula abaixo: distância em mm entre os pontos número de curvas + 1 (só se o valor das cotas seja idêntico aos valores das curvas)

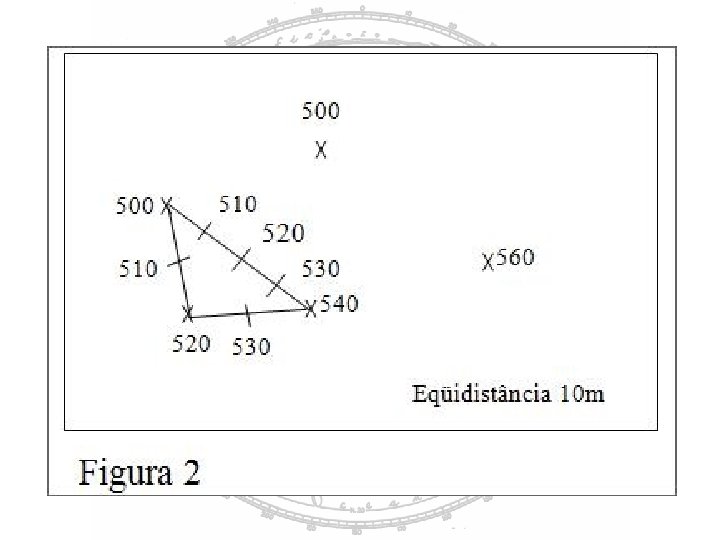
o resultado deste cálculo corresponde à distância em milímetros entre cada curva. Esta(s) distância(s) deve(m) ser plotada(s) ao longo do traço (que une as duas cotas), e o valor da(s) cota(s) deve(m) ser marcado(s) no papel (ver figura 2);

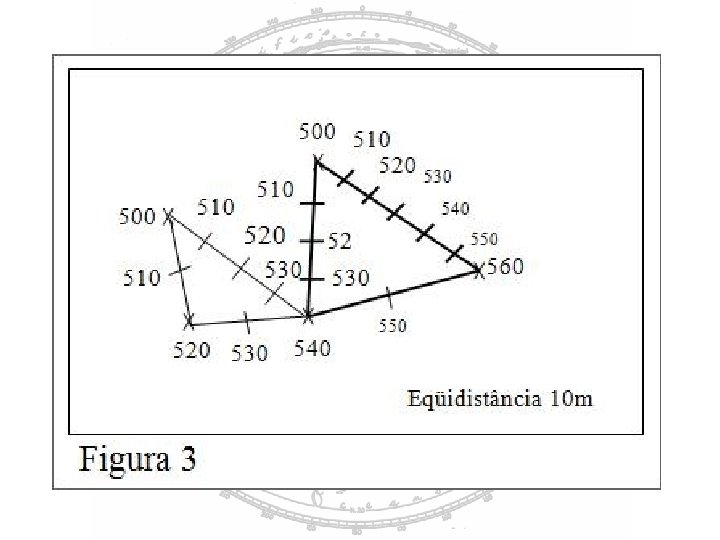
após a plotagem dos valores, repita a operação com o outro vizinho mais próximo (se houver); em caso negativo, passe para o outro vizinho mais próximo; repita estas etapas até ter interpolado todos os pontos necessários (figura 3);

Unir as cotas de mesma altitude com linhas arredondadas (figura 4), usando como orientação a hidrografia. Lembre-se que os rios correm sempre das partes mais altas para as partes mais baixas.

No terceiro exercício, onde o valor das cotas é diferente do valor das curvas (ex. cotas 243, 251 e curvas 240, 250 etc. ) deve-se calcular quanto vale, em milímetros, cada metro de altitude, procedendo da seguinte maneira: 7) Repetir os passos 1, 2, 3, e 4 da página anterior;

8) Calcular quanto vale, em milímetros, cada metro, usando a regra de três abaixo: desnível (m) está para a distância entre as cotas (mm) 1 metro está para X milímetros

Ex. cotas 346 m e 367 m distância entre as cotas 30 mm eqüidistância de 10 m: curvas de 350 e 360 367 - 346 1 m 30 x mm x = 1, 43 ou 1 m = 1, 43 mm

Se 1 m é igual a 1, 43 mm e a primeira curva acima de 346 é a curva de 350 m (diferença de 4 m), multiplica-se a diferença (desnível entre a cota e a curva), que vale 4 m, pelo valor obtido acima: 4 x 1, 43 mm = 5, 72 mm (o valor obtido corresponde à distância entre a cota mais baixa e a primeira curva acima).

10) Marcar com um ponto, na linha que une as duas cotas no desenho, a distância obtida (5, 72 mm) e anotar o respectivo valor da cota (350 m) 11) Como o valor de cada metro é conhecido e a eqüidistância é 10 m, a distância entre cada cota, a partir da cota de 350, é de 10, 43 mm (10 x 1, 43). Marcar, a cada 10, 43 mm, as cotas subseqüentes.