Rotational Puzzles on Graphs By Jaap Scherphuis For

Rotational Puzzles on Graphs By Jaap Scherphuis For G 4 G 7, 2006 1

2

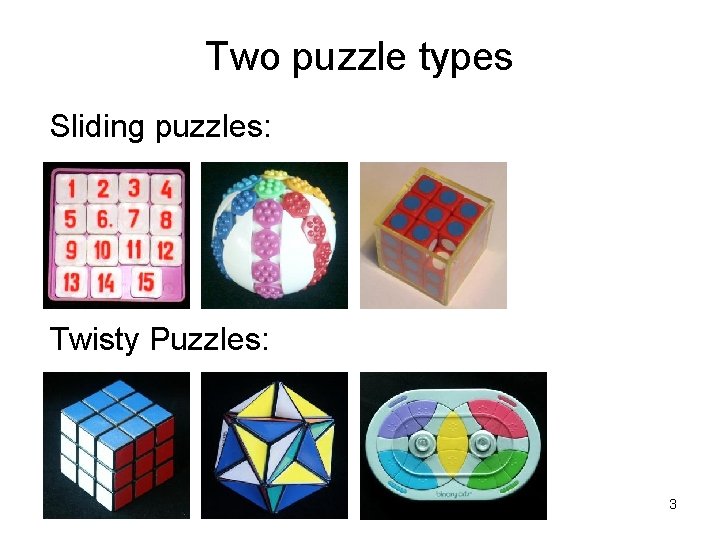
Two puzzle types Sliding puzzles: Twisty Puzzles: 3

Sliding Puzzles Richard M. Wilson “Graph Puzzles, Homotopy, and the Alternating Group” J. Combin. Theory (Series B) 16 (1974) 86 -96. 4

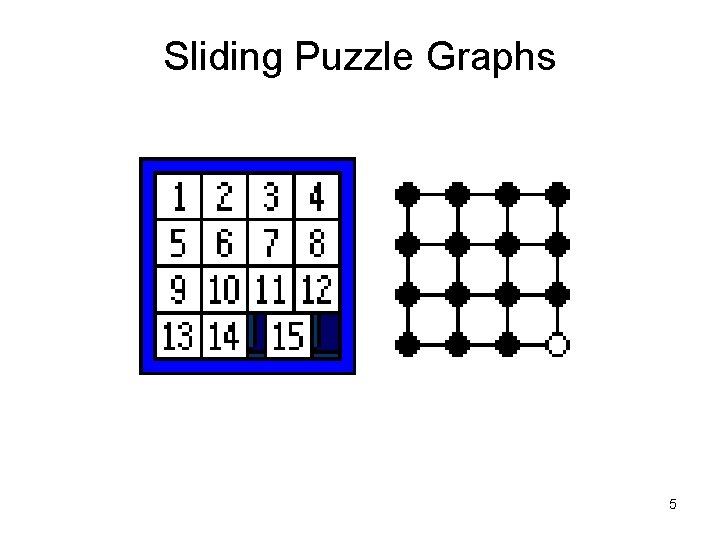
Sliding Puzzle Graphs 5

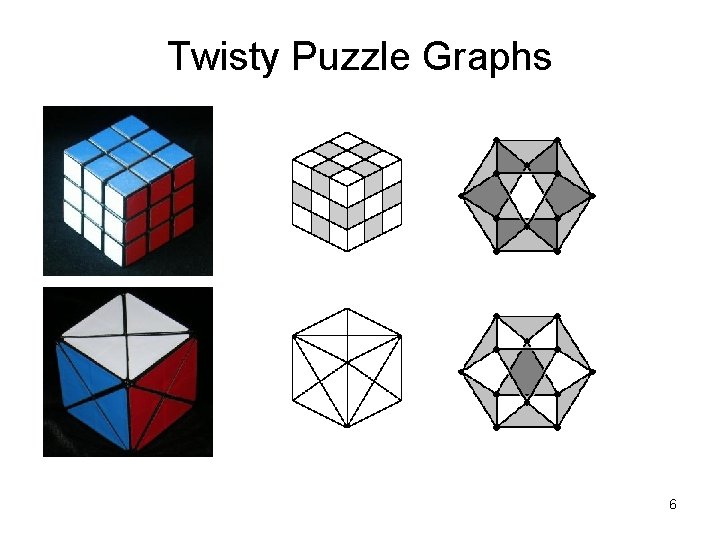
Twisty Puzzle Graphs 6

Question: Given any twisty puzzle, what positions can be achieved? Assumptions: • Puzzle given by a graph, with designated twistable faces. • Every move is a turn of one face, i. e. a cycle. • All puzzle pieces are distinguishable. • Only one type of piece. • Orientations ignored. 7

Permutation Parities Parity lemma: Let p be an odd permutation in Sn. Then <An, p>=Sn. 8

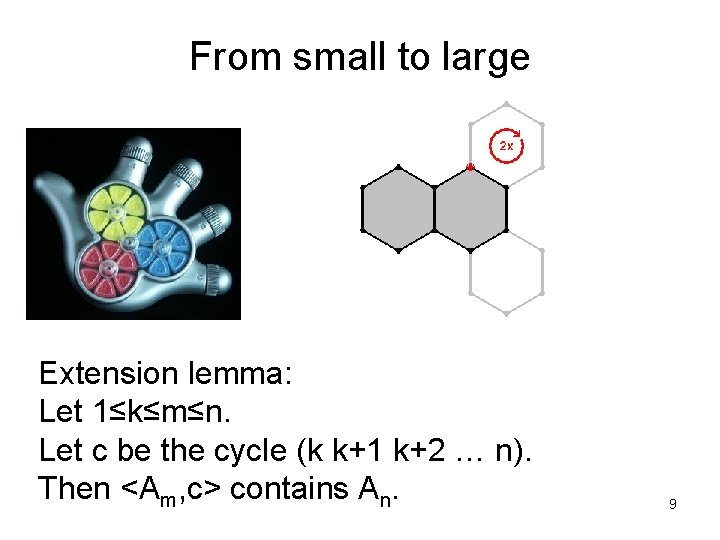
From small to large Extension lemma: Let 1≤k≤m≤n. Let c be the cycle (k k+1 k+2 … n). Then <Am, c> contains An. 9

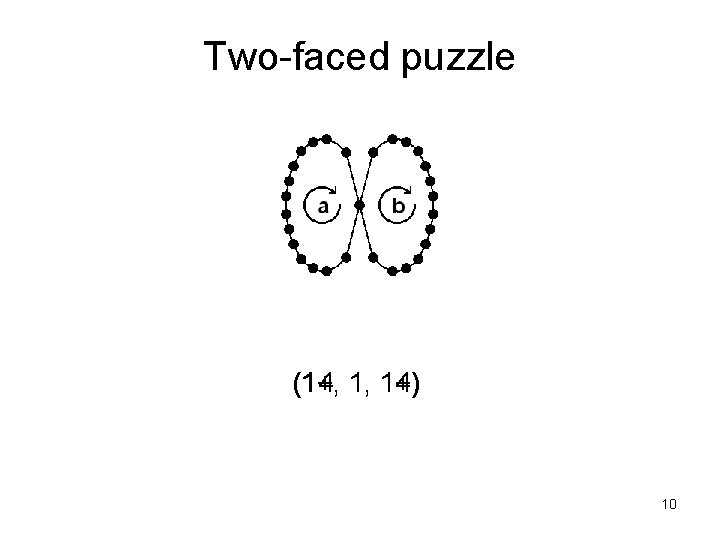
Two-faced puzzle (1+, (14, 1, 1+) 14) 10

Other two-faced puzzles Puzzle (1+, 1, 1+) (2+, 3+) (0, 2+, 1+) (1, 2+, 1) (1, 2, 2+) (1, 3, 3+) (1, 4+, 2+) (2, 3+, 2) 3 -cycle aba-1 b-1 p=b 2 a(aba-1 b-1)a-1 b-2, pap-1 a-1 aba-1 b-1 ab a (b (ab-1 a-1 b) b-1 (a-1 b-1 ab))2 ((ab-1 a-1 b) (a-1 bab-1))2 (aba-1 b-1) a-1 (a-1 b-1 ab) a (a-1 bab-1) (a-1 b-1 ab) (a-1 bab-1) 11

Two exceptional cases (2, 2, 2) (1, 3, 2) Expect: S 6, |S 6|=720 permutations Actual: PGL 2(Z 5), |PGL 2(Z 5)|=120 No 3 -cycles 12

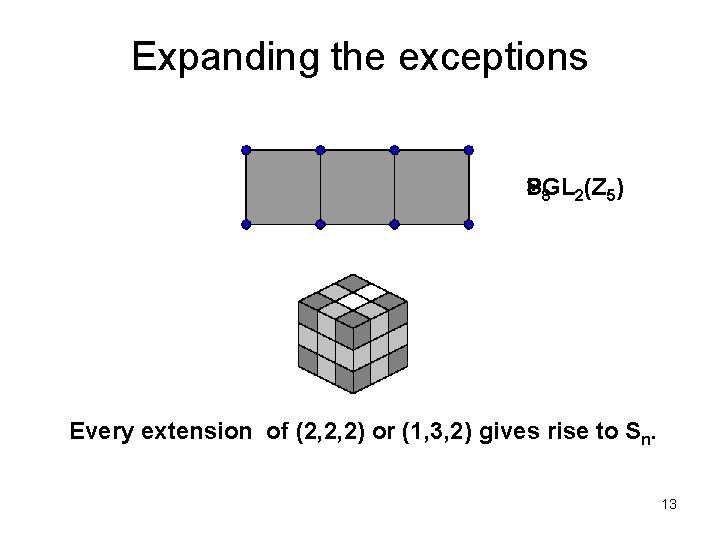
Expanding the exceptions PGL S ? 8 2(Z 5) Every extension of (2, 2, 2) or (1, 3, 2) gives rise to Sn. 13

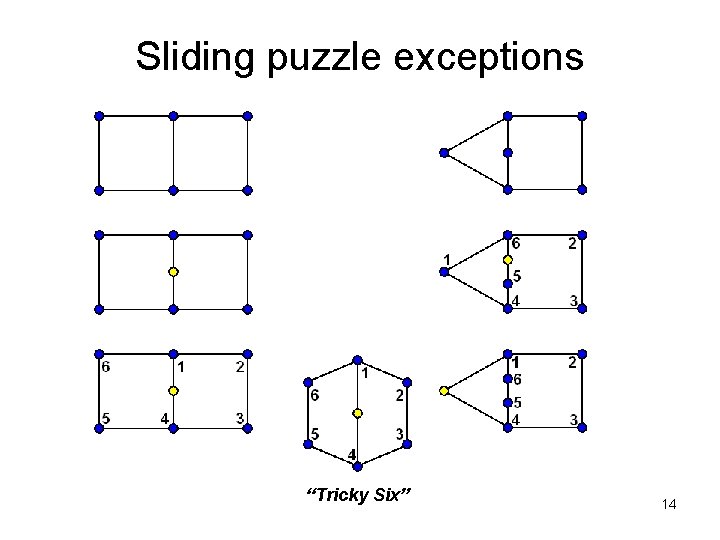
Sliding puzzle exceptions “Tricky Six” 14

Recap Nearly every rotational graph puzzle allows at least all even permuations. Exceptions: • Trivial: Polygon, one face – Cyclic group • Interesting: Two graphs – PGL 2(Z 5) • Other: No pair of faces with single overlap. 15

Richard M. Wilson “Graph Puzzles, Homotopy, and the Alternating Group” J. Combin. Theory (Series B) 16 (1974) 86 -96. Jaap Scherphuis Jaap’s Puzzle Page https: //www. jaapsch. net/puzzles/ 16