Rotational mechanics How can you change the rotational

Rotational mechanics How can you change the rotational motion of an object?

Take any object and apply a force to make it spin… n n n How many different ways can you make it spin? How many different axes of rotation can you discover? At what point on the object do you have to apply this force?

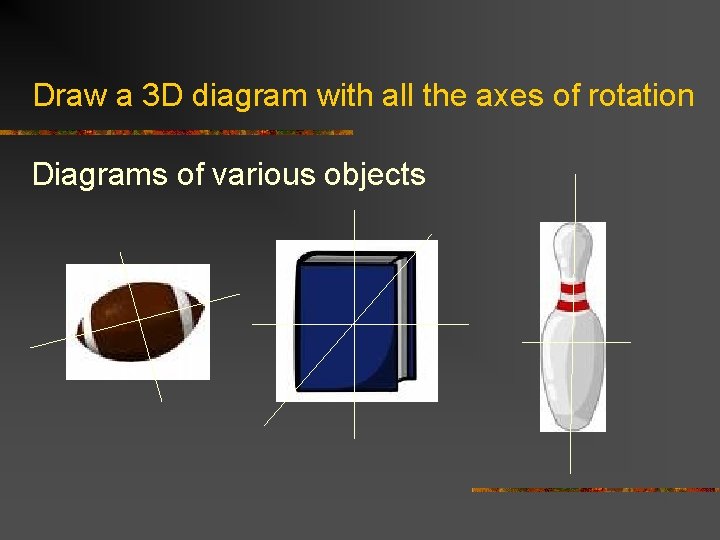
Draw a 3 D diagram with all the axes of rotation Diagrams of various objects

Observation: axes of rotation intersect! n n n Intersection is at geometric center for objects that are symmetrical, same material and solid throughout Intersection is not at geometric center for oddly shaped or not same material Intersection can be in empty space, outside the actual object: boomerang!

Observation: the axes all intersect at one point n What does this mean? It’s the location of the ‘center of gravity’ or ‘center of mass’ n The entire weight or mass of an object can be considered concentrated at this one location for purposes of physics calculations

Are CG and CM the same or not? n CG takes into account the effects of gravity or gravitational fields n If a gravitational field is uniform over the whole object, ‘g’ is the same up and down, left and right, then CG and CM are the same spot n When might a gravitional field vary? For extremely large objects or systems such as planetary systems n Even for skyscrapers, CG and CM are only millimeters apart

Other ways to find the CG? n n Try to balance the object The location of the CG will be in a vertical line with the balance point or over the base of support

How did you apply the force? n Push or pull at some point on the edge, on one edge or both in opposite directions force

Would it spin if you pushed through the CG? n n A force through the CG only affects the linear motion Won’t make it spin

Lever arm n The distance between the point at which you apply the force AND the axis of rotation is the LEVER ARM, d d Axis of rotation

What is the most efficient way to apply the force? n Perpendicular to the lever arm n You can apply the force at any angle you want (with respect to the lever arm) n In that case, the equation becomes n n Torque = force x lever arm x cosine of the angle between the force and the lever arm When force is perpendicular , angle is 90 degrees and cosine 90 is 1 !!

Analogy to Newton’s laws n If force can cause a change in linear motion, then…. n A force applied at a point other than the CG can cause a change in ……

A change in rotational motion!! n n Torque causes a change in rotational motion All of Newton’s laws apply! Yay Newton!! n If force is applied perpendicular to the lever arm, then n Torque = force F x lever arm d

Since all of Newton’s laws apply… n If the sum of the torques = 0, n Then the object’s rotational motion will not change n Wasn’t rotating…. still not rotating n n (static equilibrium) Was rotating…continues at the same rate

Since all of Newton’s laws apply… n If the sum of the torques is NOT = 0, n Then the object’s rotational motion WILL change, it will acclerate in an angular or rotational sense n Wasn’t rotating…. starts to rotate n Was rotating…rate of rotation is changed

Demos from class… n If we push on the shoulders in the same direction, do we make him spin? Why, why not?

Demos from class… n If we push on the shoulders in the opposite directions, do we make him spin? Why, why not?

Activity from class. . . Newton’s 1 st law…. n Weighing an elephant (balancing a meterstick) n Observations of balanced system n n n Heavier wts. closer to pivot pt Lighter wts. farther away from pivot pt Mathematical relationship n Torque on left side = torque on right side n n Fxd = Fxd Balanced torques…. . sum of the torques = 0

Thoughts from class… n Multiple weights? 2 on left, 1 on right? ? n n Add up torques (F 1 x d 1) + (F 2 x d 2) = ( F 3 x d 3)

Pivot NOT at the CG? n Can you balance the stick if the pivot is NOT at the CG? n The weight acting through the CG causes a torque on the right side n n Torque = wt x (dist between CG and pivot) Must place a weight on left side to create an equal and opposite torque!

Why are some objects easier to rotate than others? n Remember resistance to motion? ? ? n What was that called again? n n _______ What might resistance to rotational motion be called? n _________

Plain old inertia depended on… n MASS! n F = ma n A lot of mass, a lot of resistance to linear motion n Less acceleration for the same force, etc.

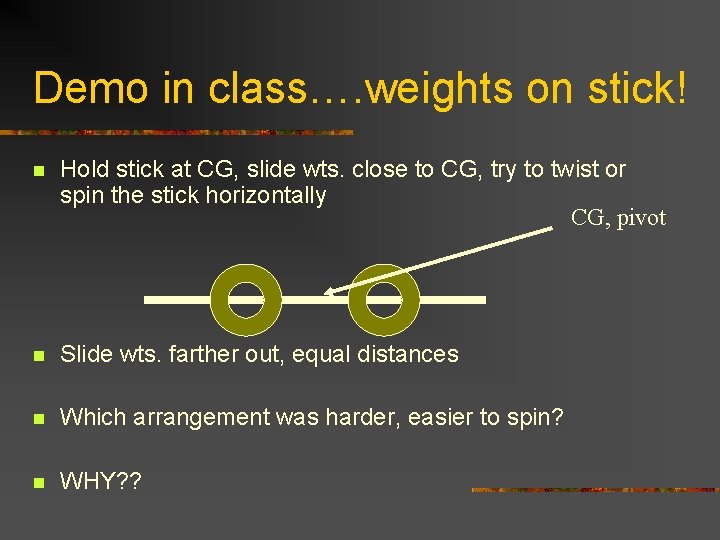
Demo in class…. weights on stick! n Hold stick at CG, slide wts. close to CG, try to twist or spin the stick horizontally CG, pivot n Slide wts. farther out, equal distances n Which arrangement was harder, easier to spin? n WHY? ?

You changed the rotational inertia! n Rotational inertia depends on n n Mass Distribution of that mass Relation to the intended axis of rotation We could have made it even harder if we grabbed it by the end and tried to spin it along that axis!

Refer to book formulas for regular shapes n I is the letter variable for rotational inertia, aka n n Moment of inertia Notice that for a hoop of same mass, size n if hoop is rolled (axis of rotation is parallel to length), n n I is greater, = mr 2 if hoop is spun like a top (axis of rotation is vertical ), n I is less, = ½ mr 2

Demo in class with hoop and solid disk… n Which one rolled to bottom of ramp first? n WHY? n With disks of same mass and size, disk of less I, less resistance to rolling, accelerates down the ramp at a greater rate, and wins the race!!

Rotational inertia and gymnastics n You can rotate your body (in theory!) around at least three different axes Longitudinal (spinning like a ballerina, ice skater) n Transverse (flip, somersault) n Medial (cartwheel) n n n Which one presents the lowest I? How many ways have you ever rotated your body? ?

Other analogies from linear motion? n Linear momentum p = mass x velocity… n Angular momentum L = n n Moment of inertia I x angular velocity Conservation of linear momentum… n Conservation of angular momentum n Example in class – person spins faster on stool when he brings arms in, thereby reducing rotational inertia, and vice versa

Also refer to handouts from class