Rotational Kinematics Angular Position Angular Position 0 0

Rotational Kinematics

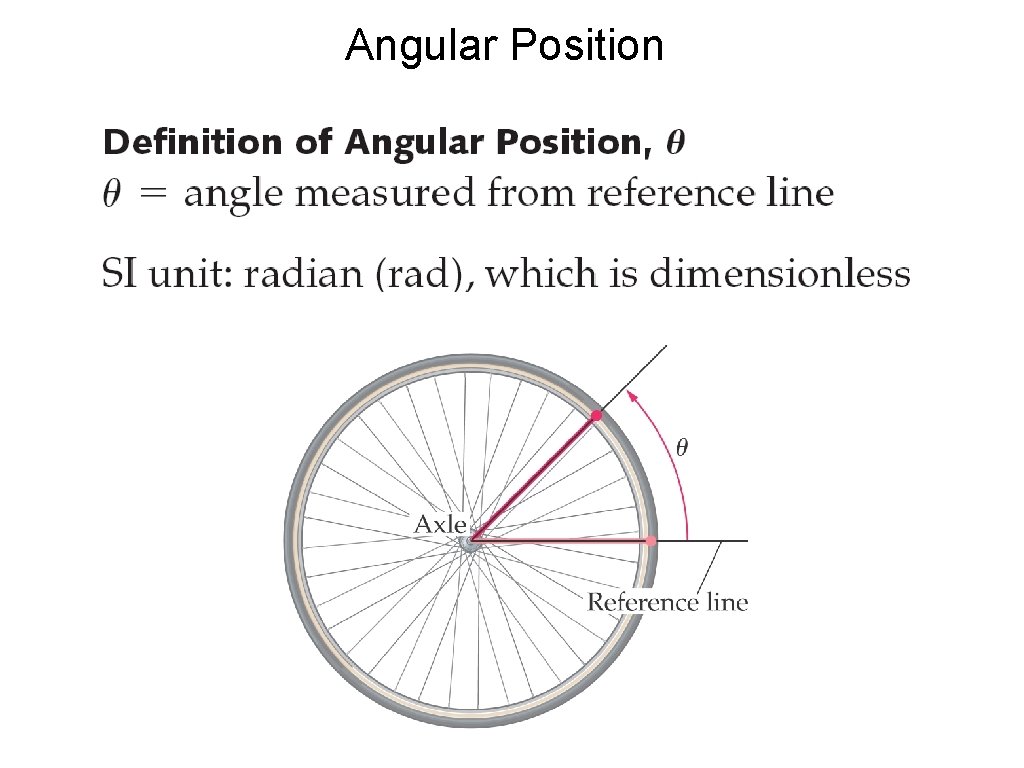
Angular Position

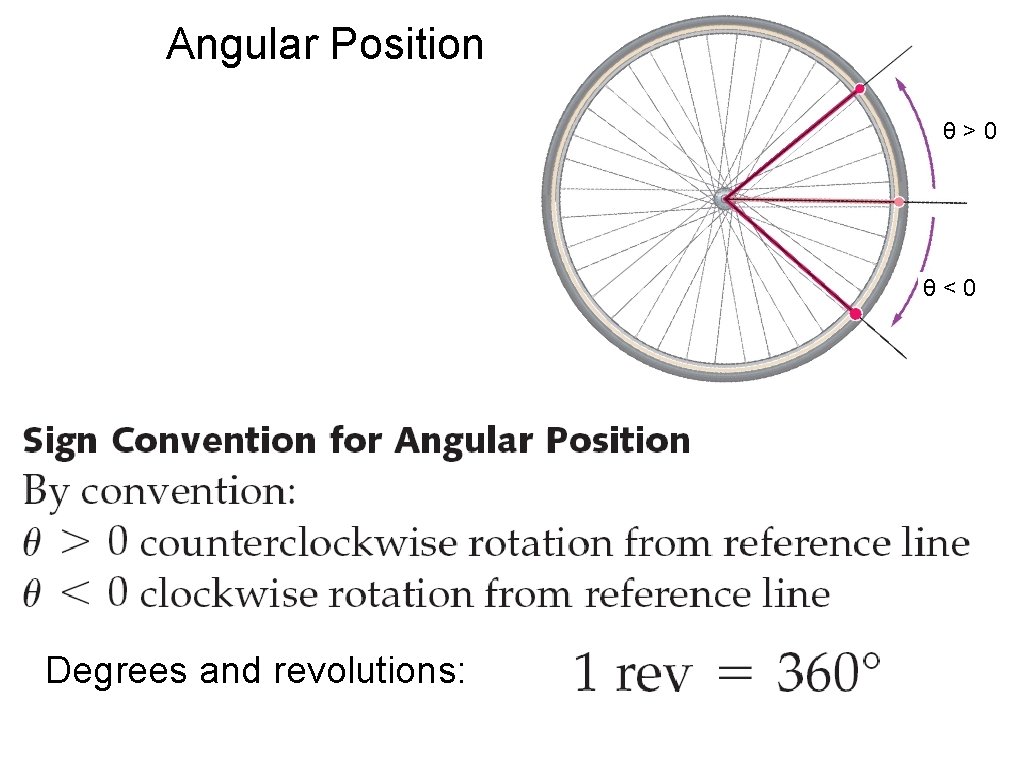
Angular Position θ>0 θ<0 Degrees and revolutions:

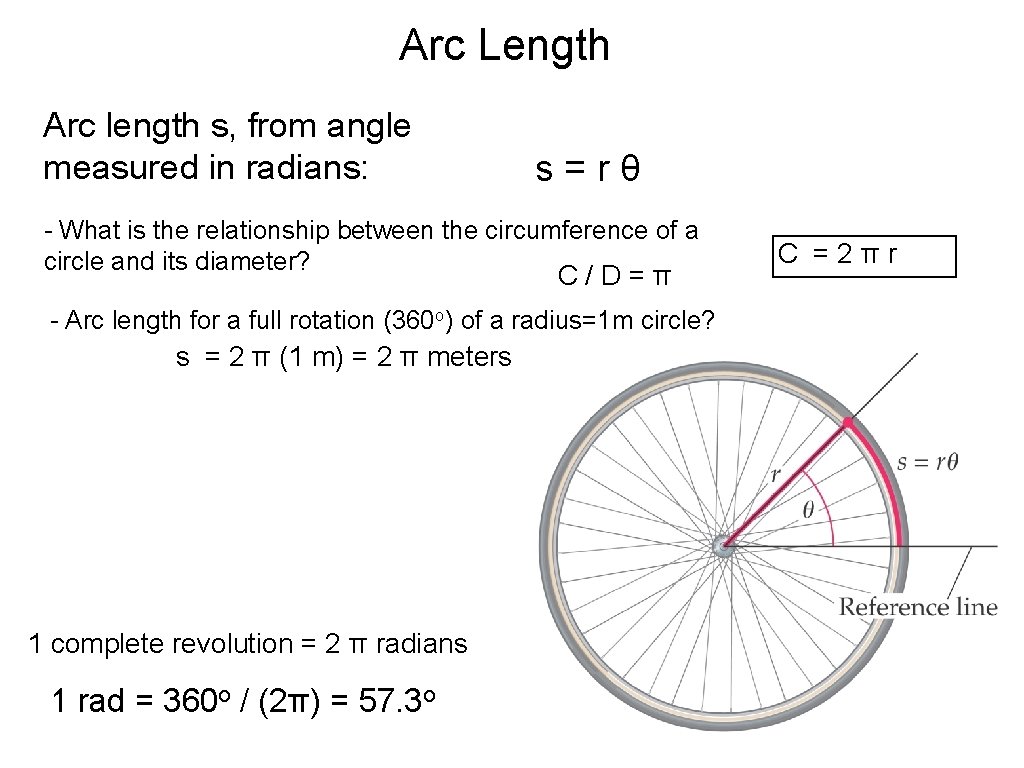
Arc Length Arc length s, from angle measured in radians: s=rθ - What is the relationship between the circumference of a circle and its diameter? C/D=π - Arc length for a full rotation (360 o) of a radius=1 m circle? s = 2 π (1 m) = 2 π meters 1 complete revolution = 2 π radians 1 rad = 360 o / (2π) = 57. 3 o C =2πr

Why use radians? • Doesn’t involve arbitrary choice of 360 degrees. There is another unit, the gon or gradian that is used in surveying: • Radians useful for small angles: 5

Angular Velocity

Instantaneous Angular Velocity Period = How long it takes to go 1 full revolution Period T: SI unit: second, s

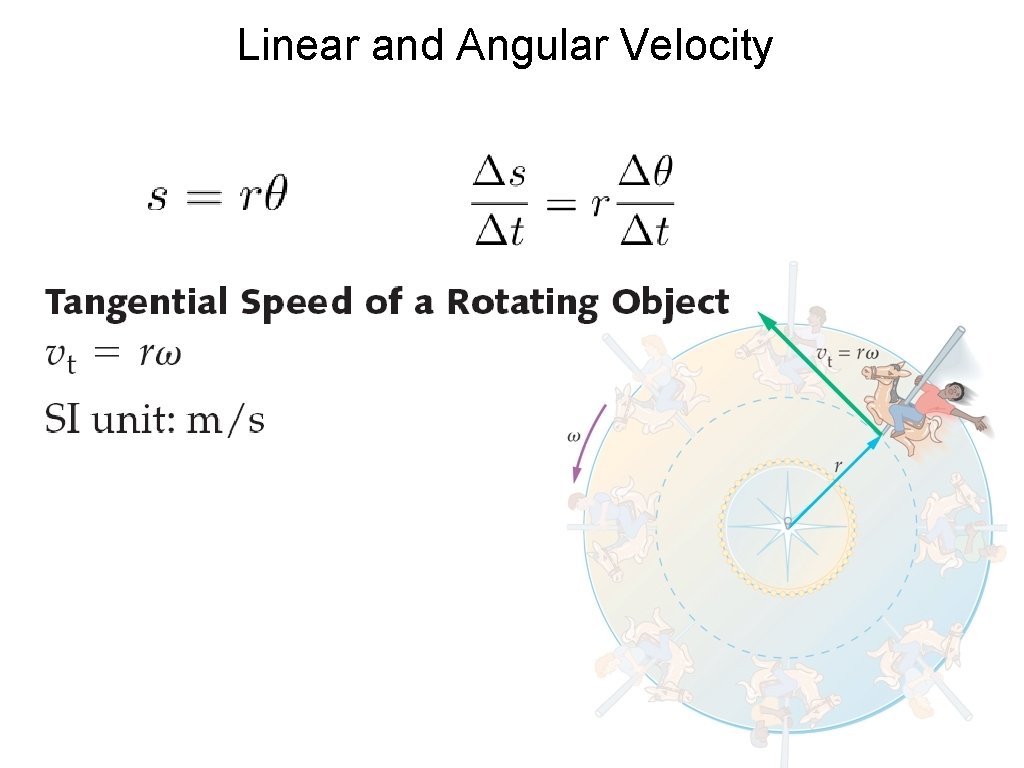
Linear and Angular Velocity

Greater translation for same rotation

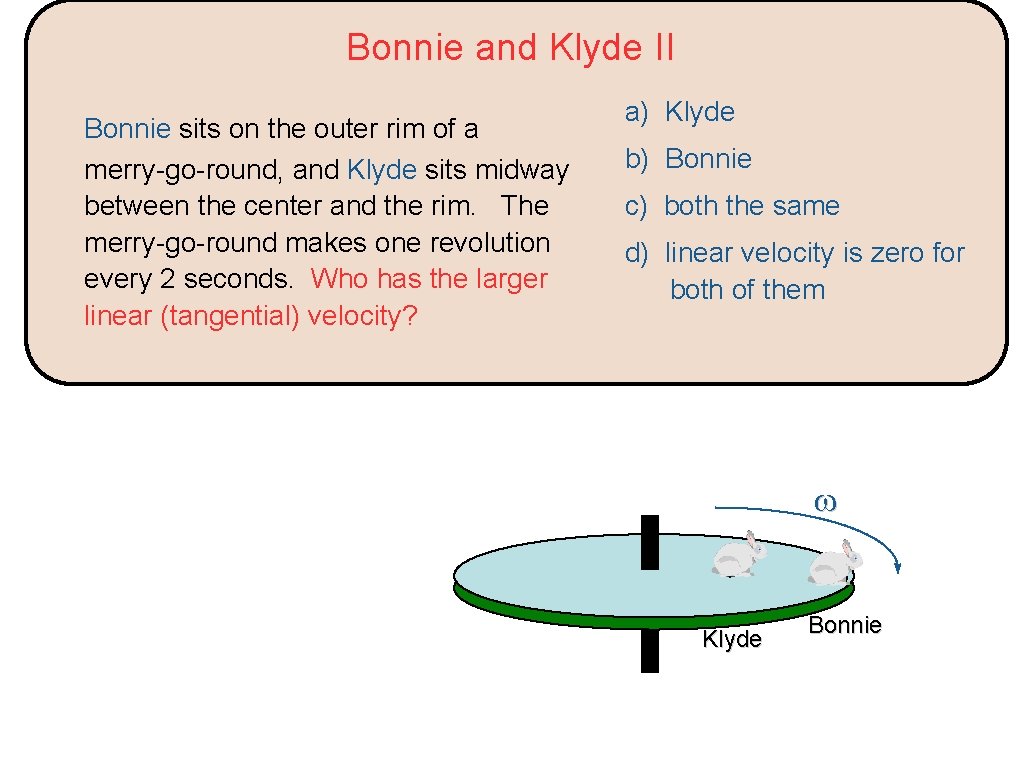
Bonnie and Klyde II Bonnie sits on the outer rim of a merry-go-round, and Klyde sits midway between the center and the rim. The merry-go-round makes one revolution every 2 seconds. Who has the larger linear (tangential) velocity? a) Klyde b) Bonnie c) both the same d) linear velocity is zero for both of them Klyde Bonnie

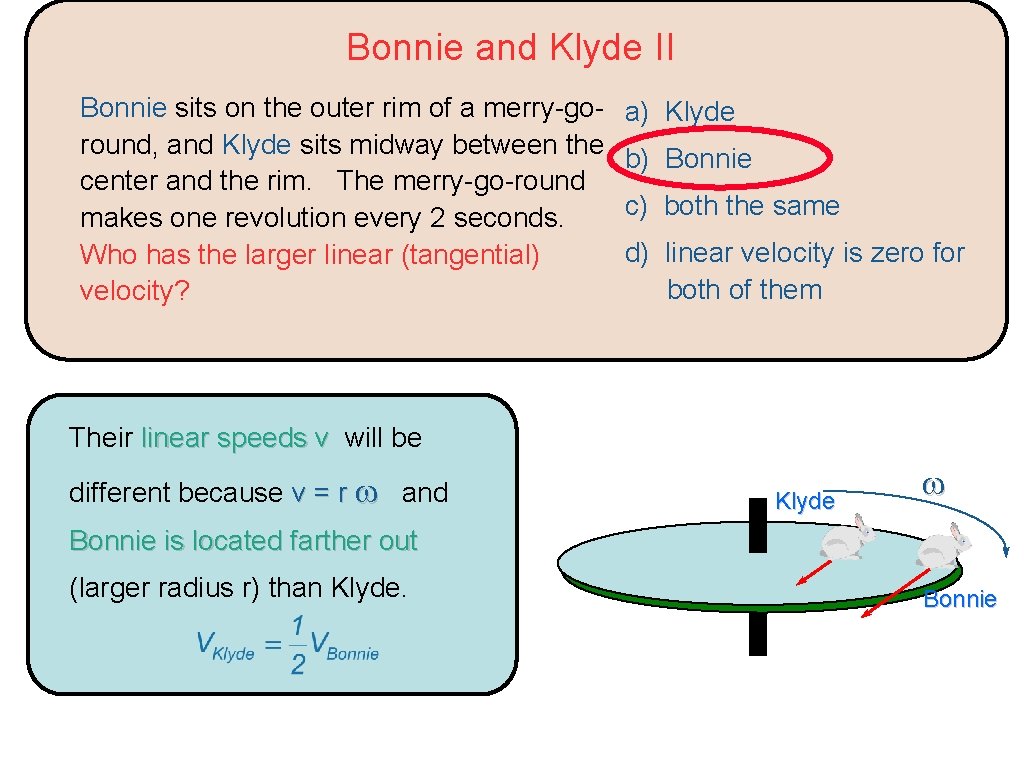
Bonnie and Klyde II Bonnie sits on the outer rim of a merry-goround, and Klyde sits midway between the center and the rim. The merry-go-round makes one revolution every 2 seconds. Who has the larger linear (tangential) velocity? a) Klyde b) Bonnie c) both the same d) linear velocity is zero for both of them Their linear speeds v will be different because v = r and Klyde Bonnie is located farther out (larger radius r) than Klyde. Bonnie

Angular Acceleration

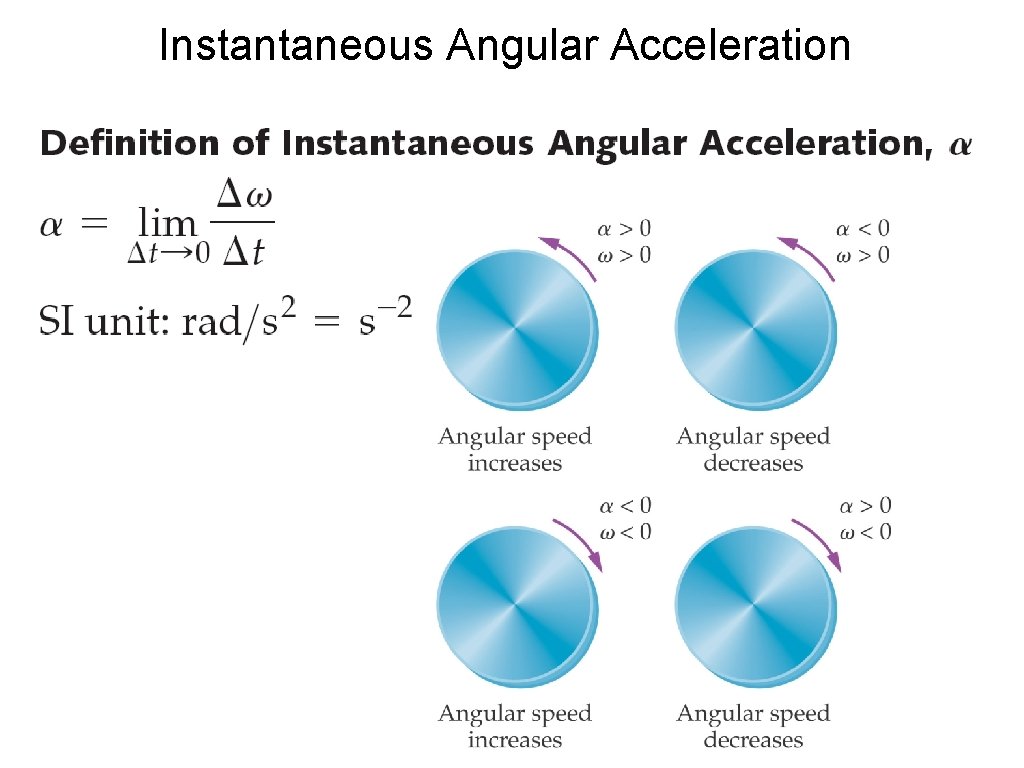
Instantaneous Angular Acceleration

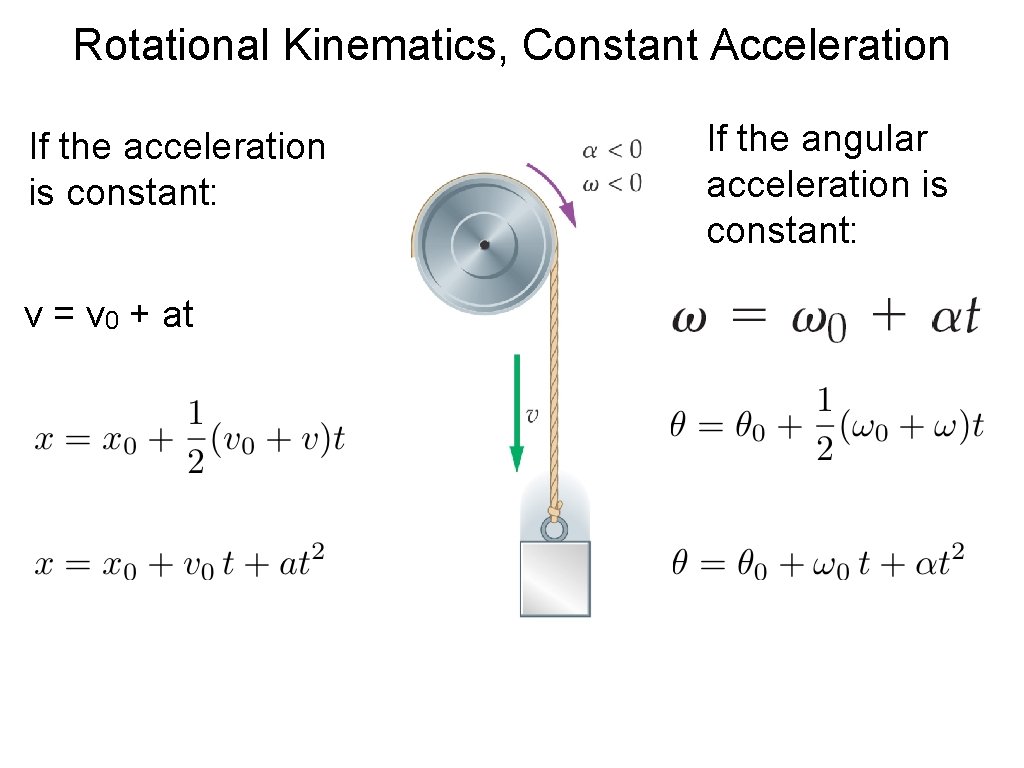
Rotational Kinematics, Constant Acceleration If the acceleration is constant: v = v 0 + at If the angular acceleration is constant:

Analogies between linear and rotational kinematics:

Angular Displacement I a) ½ An object at rest begins to rotate with a constant angular acceleration. If this object rotates through an angle in the time t, through what angle did it rotate in the time t? ½ b) ¼ c) ¾ d) 2 e) 4

Angular Displacement I a) ½ An object at rest begins to rotate with a constant angular acceleration. If this object rotates through an angle in the time t, through what angle did it rotate in the time t½ ? The angular displacement is = b) ¼ c) ¾ d) 2 e) 4 t 2 (starting from rest), and there is a quadratic dependence on time. Therefore, in half the time, time the object has rotated through one-quarter the angle

Which child experiences a greater acceleration? (assume constant angular speed)

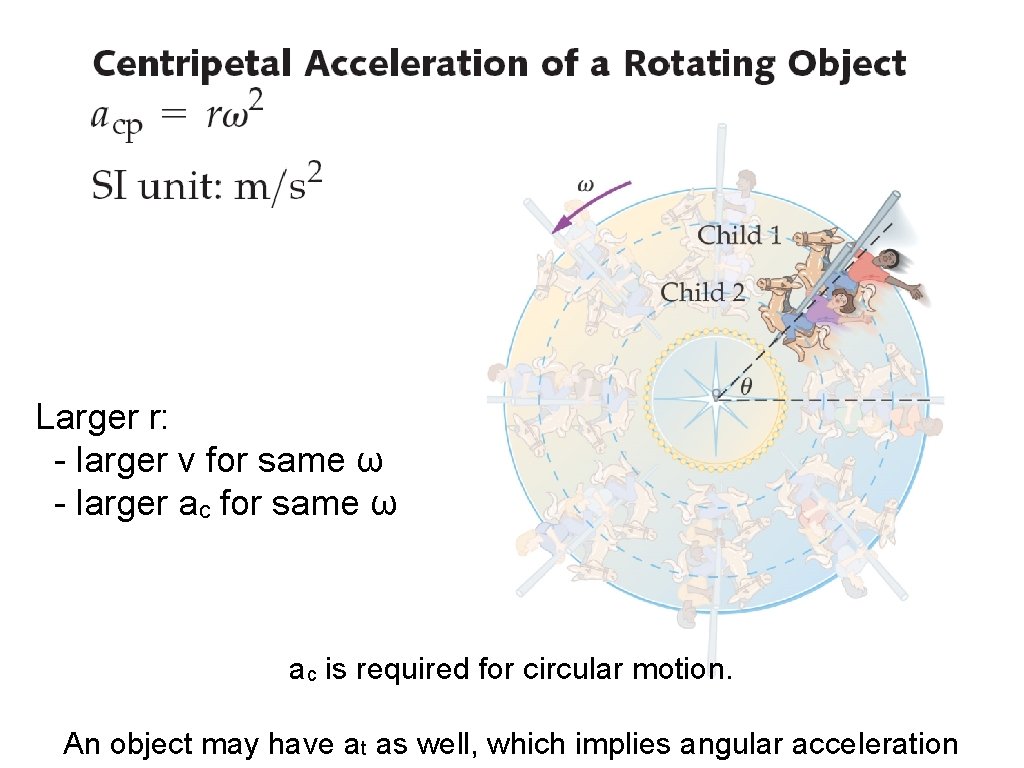
Larger r: - larger v for same ω - larger ac for same ω ac is required for circular motion. An object may have at as well, which implies angular acceleration

Angular acceleration and total linear acceleration

Angular and linear acceleration

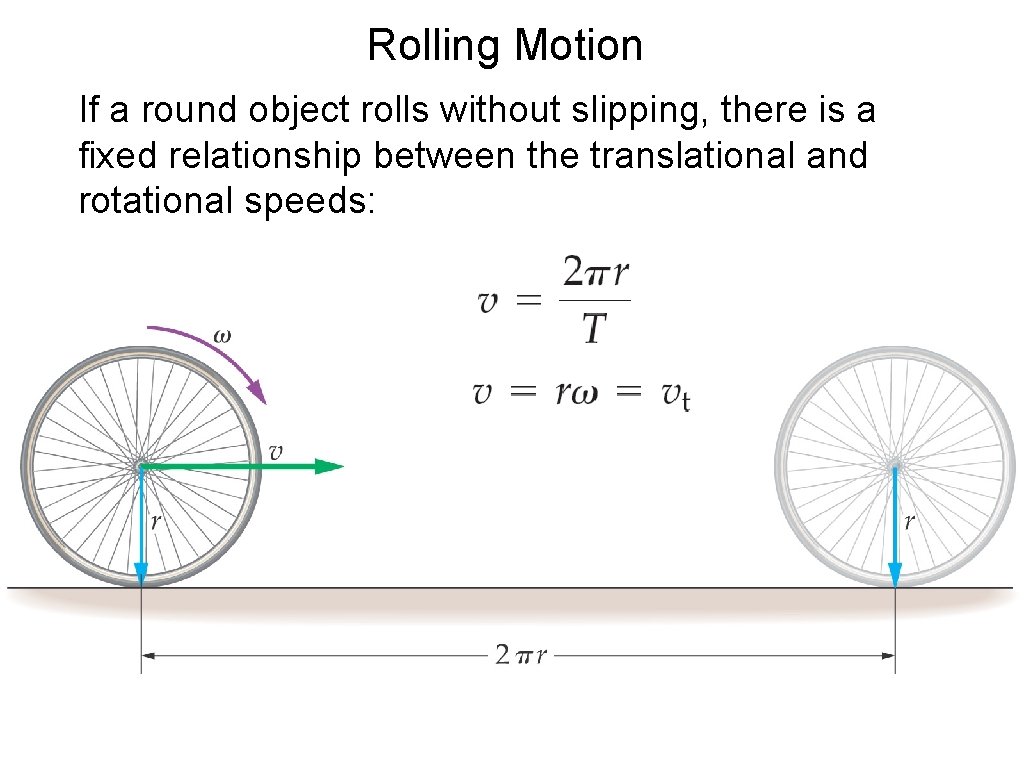
Rolling Motion If a round object rolls without slipping, there is a fixed relationship between the translational and rotational speeds:

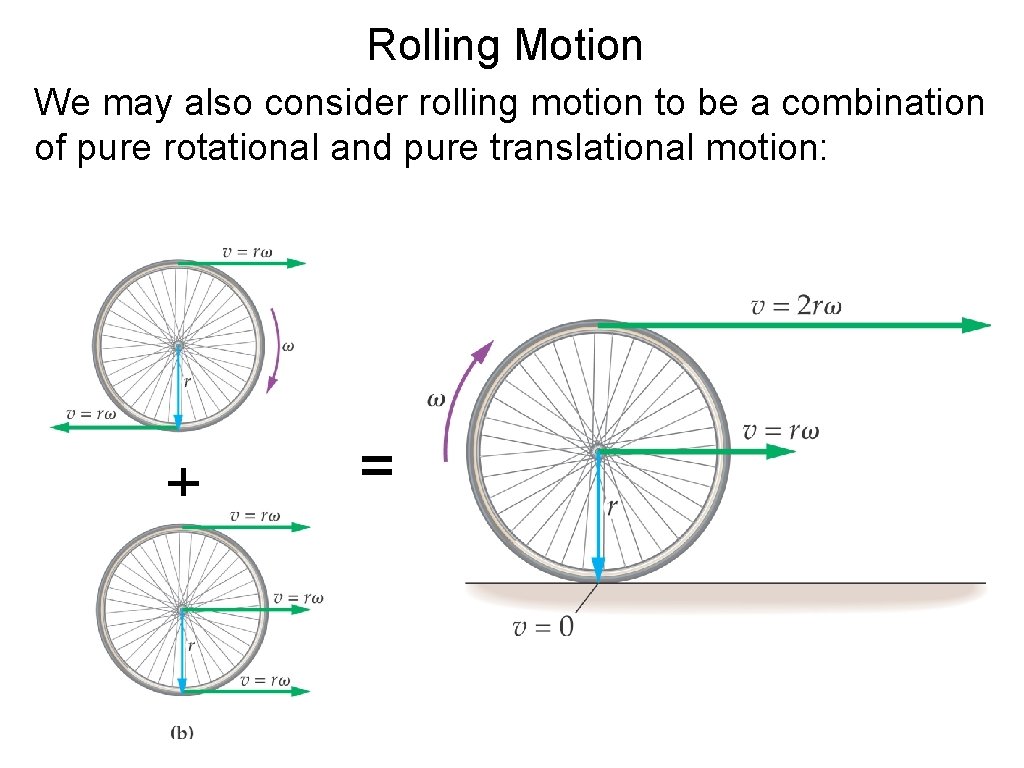
Rolling Motion We may also consider rolling motion to be a combination of pure rotational and pure translational motion: + =

Jeff of the Jungle swings on a vine that is 7. 20 m long. At the bottom of the swing, just before hitting the tree, Jeff’s linear speed is 8. 50 m/s. (a) Find Jeff’s angular speed at this time. (b) What centripetal acceleration does Jeff experience at the bottom of his swing? (c) What exerts the force that is responsible for Jeff’s centripetal acceleration? a) b) c) This is the force that is responsible for keeping Jeff in circular motion: the vine.