Rotational Dynamics TranslationalRotational Analogues Connections Continue Displacement Velocity

Rotational Dynamics

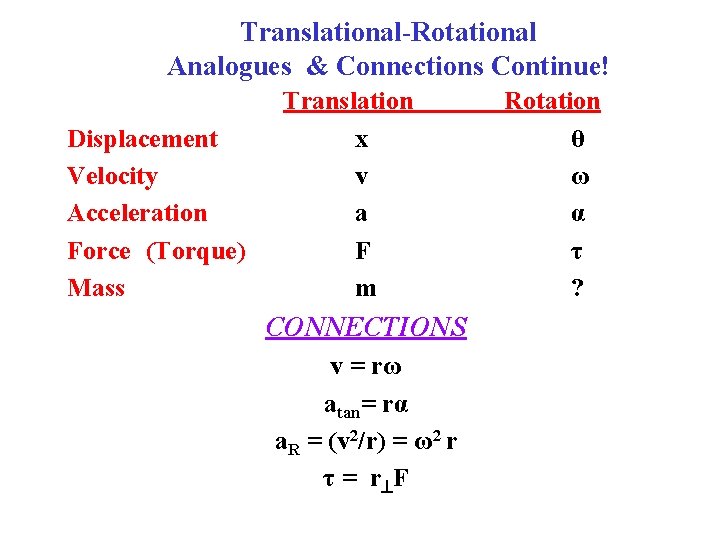
Translational-Rotational Analogues & Connections Continue! Displacement Velocity Acceleration Force (Torque) Mass Translation x v a F m CONNECTIONS v = rω atan= rα a. R = (v 2/r) = ω2 r τ = r F Rotation θ ω α τ ?

• Goal: Newton’s 2 nd Law for rotational motion. • We’ve just seen: The angular acceleration is the net torque or α τnet = ∑τ = sum of torques Analogous to Newton’s 2 nd Law: a Fnet = ∑F = sum of forces – Recall, Newton’s 2 nd Law: ∑F = ma. a α , F τ • Question: What plays the role of mass m for rotational problems?

Simplest Possible Case A mass m moving in a circle of radius r, one force F TANGENTIAL to the circle τ = r. F Newton’s 2 nd Law + relation (a = rα) between tangential & angular accelerations F = ma = mrα So τ = mr 2α Newton’s 2 nd Law for Rotations Proportionality constant between τ & α is mr 2 (point mass only!)

For one particle, moving in a circle, Newton’s 2 nd Law for rotational motion is: τ = mr 2α • Extrapolate to a rigid body, made of many particles. Newton’s 2 nd Law, rotational motion becomes ∑τ = ∑(mr 2)α – Since α is the same for all points in the body, it comes out sum over all point masses in the body of the sum. Write ∑τ = Iα, where the proportionality constant I = ∑(mr 2) = m 1 r 12 + m 2 r 22 + m 3 r 32 + … Moment of Inertia of the body

Newton’s 2 nd Law, rotational motion is: The net torque = (moment of inertia) (angular acceleration) • Moment of Inertia of the body: • Moment of Inertia I = A measure of the rotational inertia of the body. Analogous to the mass m = A measure of translational inertia of the body.

Translational-Rotational Analogues & Connections Translation Displacement x Velocity v Acceleration a Force (Torque) F Mass (moment of inertia) m Rotation θ ω α τ I CONNECTIONS v = rω, atan= rα, a. R = (v 2/r) = ω2 r τ = r F , I = ∑(mr 2) NEWTON’S 2 nd LAW: ∑F = ma; ∑τ = Iα

Obtained for simple shaped bodies using calculus. Useful for problem solving!

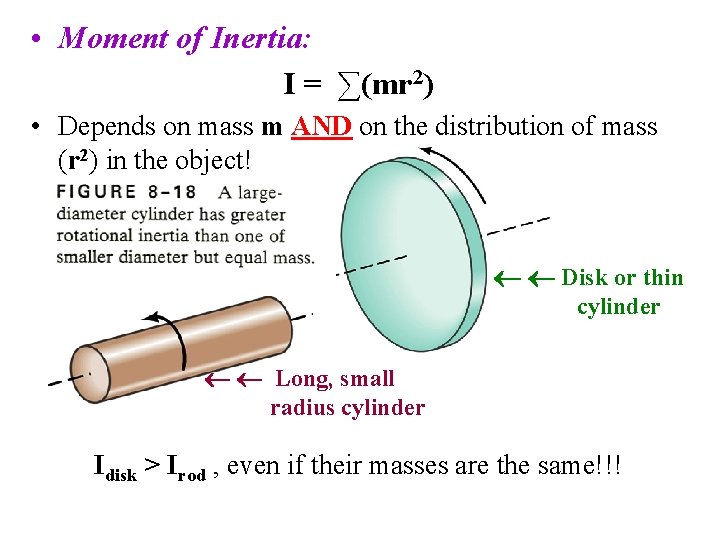
• Moment of Inertia: I = ∑(mr 2) • Depends on mass m AND on the distribution of mass (r 2) in the object! Disk or thin cylinder Long, small radius cylinder Idisk > Irod , even if their masses are the same!!!

Example I = ∑(mr 2) a) I = (5)(2)2 +(7)(2)2 = 48 kg m 2 b) I = (5)(0. 5)2 + (7)(4. 5)2 = 143 kg m 2 NOTE! I depends on the rotation axis and on the mass distribution