Rotational Dynamics Continued TranslationRotation Analogues Connections Translation Rotation

Rotational Dynamics Continued

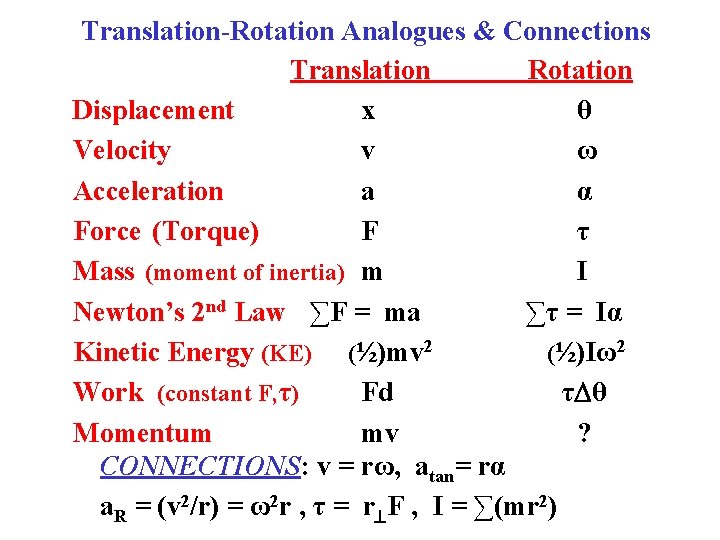
Translation-Rotation Analogues & Connections Translation Rotation Displacement x θ Velocity v ω Acceleration a α Force (Torque) F τ Mass (moment of inertia) m I Newton’s 2 nd Law ∑F = ma ∑τ = Iα Kinetic Energy (KE) (½)mv 2 (½)Iω2 Work (constant F) Fd ? CONNECTIONS: v = rω, atan= rα a. R = (v 2/r) = ω2 r , τ = r F , I = ∑(mr 2)

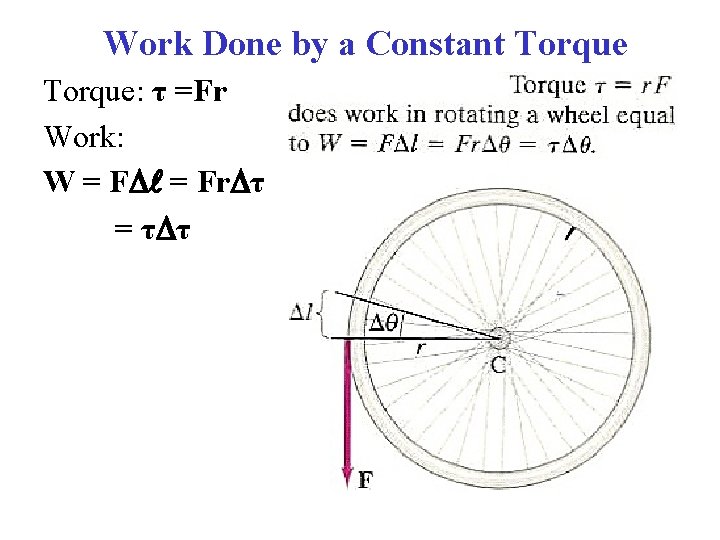
Work Done by a Constant Torque: τ =Fr Work: W = Fr τ = τ τ

Translation-Rotation Analogues & Connections Translation Rotation Displacement x θ Velocity v ω Acceleration a α Force (Torque) F τ Mass (moment of inertia) m I Newton’s 2 nd Law ∑F = ma ∑τ = Iα Kinetic Energy (KE) (½)mv 2 (½)Iω2 Work (constant F, τ) Fd τ θ Momentum mv ? CONNECTIONS: v = rω, atan= rα a. R = (v 2/r) = ω2 r , τ = r F , I = ∑(mr 2)

Angular Momentum • Define: Angular Momentum of rotating body (moment of inertia I, angular velocity ω): L Iω (kg m 2/s) • Recall, general Newton’s 2 nd Law: ∑F = ( p/ t) (= ma) if ∑F = 0, ( p/ t) = 0 & p = constant Momentum is conserved if the total force = 0 (collisions!)

• Angular Momentum L Iω • Similar to momentum case, can show, rotational version of Newton’s 2 nd Law: ∑τ = ( L/ t) (= Iα) if ∑τ = 0, ( L/ t) = 0 & L = constant Angular Momentum is conserved if total torque = 0 • Example: t = 0, angular velocity ω0 time t, angular velocity ω L = L 0 or Iω = I 0ω0 Change moment of inertia from I 0 to I by changing the body’s shape!

Conservation of Angular Momentum means: • So, if an object’s moment of inertia changes, its angular speed also must change! • Example Ice skater: L Iω But I = ∑(mr 2) Iω = I 0ω0

Conservation of Angular Momentum means: • So, if an object’s moment I 1ω1 of inertia changes, its angular speed also must change! • Example Diver: L Iω But I = ∑(mr 2) So, Iω = constant I 2ω2 I 3ω3 Center of Mass I 1ω1 = I 2ω2 = I 3ω3 = I 4ω4

Example: An object rotating on a string of changing length. A small mass m is attached to the end of a string. It revolves in a circle on a frictionless tabletop. The other end of the string passes through a hole in the table. Initially, it revolves with a speed v 1 = 2. 4 m/s in a circle of radius r 1 = 0. 80 m. The string is pulled slowly through the hole so that the radius is reduced to r 2 = 0. 48 m. What is the new speed, v 2, of the mass? v 1 = 2. 4 m/s, r 1 = 0. 8 m, r 2 = 0. 48 m, v 2 = ? Solution: Conservation of Angular Momentum So, L = I 1ω1 = I 2ω2 or m(r 1)2ω1 = m(r 2)2ω2 Giving ω2 = ω1 (r 2)2/(r 1)2 , ω1 = (v 1/r 1) And v 2 = r 2ω2 = r 2(v 1/r 1)[(r 2)2/(r 1)2] = v 1 (r 1/r 2) So, v 2 = 4. 0 m/s

Angular Quantities are Vectors! The defined direction of the angular velocity vector ω is to the plane of rotation. The vector directions of the angular acceleration α and the angular momentum L = Iω are similarly to the rotation Plane. The direction of these vectors is given by the “Right-Hand Rule”.

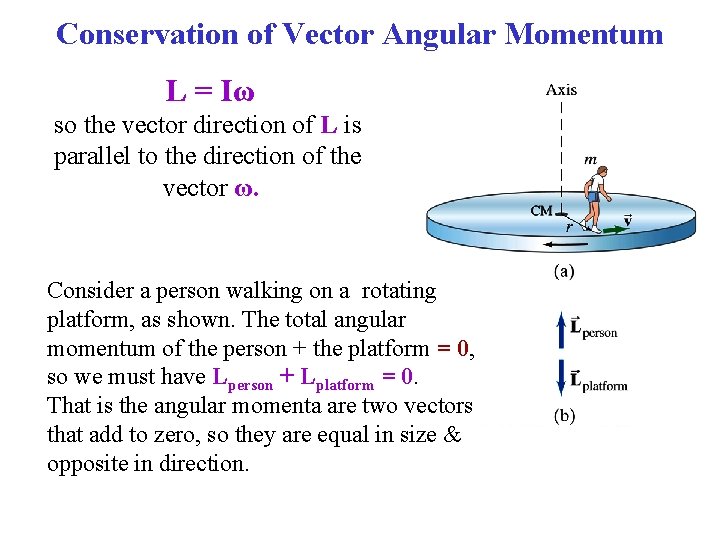
Conservation of Vector Angular Momentum L = Iω so the vector direction of L is parallel to the direction of the vector ω. Consider a person walking on a rotating platform, as shown. The total angular momentum of the person + the platform = 0, so we must have Lperson + Lplatform = 0. That is the angular momenta are two vectors that add to zero, so they are equal in size & opposite in direction.

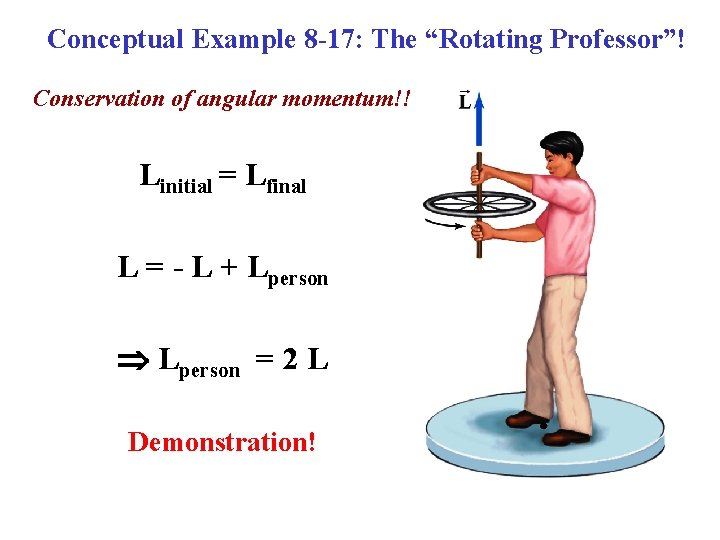
Conceptual Example 8 -17: The “Rotating Professor”! Conservation of angular momentum!! Linitial = Lfinal L = - L + Lperson = 2 L Demonstration!

Translation-Rotation Analogues & Connections Translation Rotation Displacement x Velocity v Acceleration a Force (Torque) F Mass (moment of inertia) m Newton’s 2 nd Law ∑F = ma Kinetic Energy (KE) (½)mv 2 Work (constant F, τ) Fd Momentum mv CONNECTIONS: v = rω, θ ω α τ I ∑τ = Iα (½)Iω2 τ θ Iω atan= rα a. R = (v 2/r) = ω2 r , τ = r F , I = ∑(mr 2)

Another “Rotating Professor”! Demonstration!!