Rotation Matrices and Quaternion Siamak Faal 12 04202016

Rotation Matrices and Quaternion Siamak Faal 1/2 04/20/2016 1

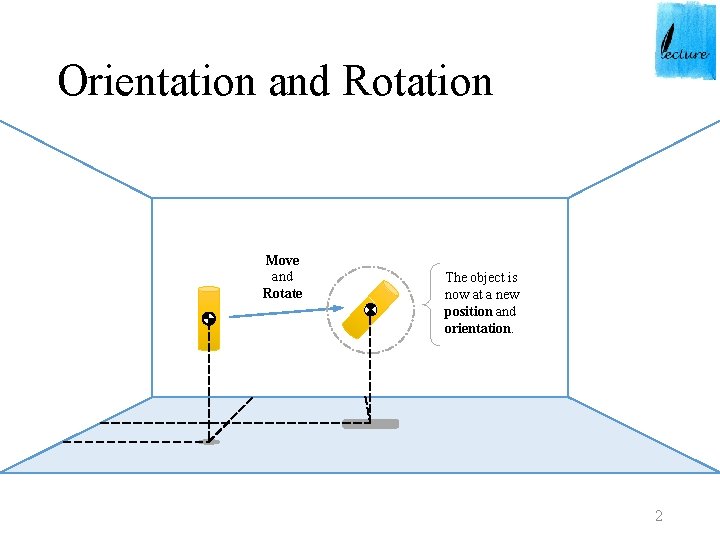
Orientation and Rotation Move and Rotate The object is now at a new position and orientation. 2

Orientation and Rotation Matrices Quaternion 3

Preliminaries and notations • 4

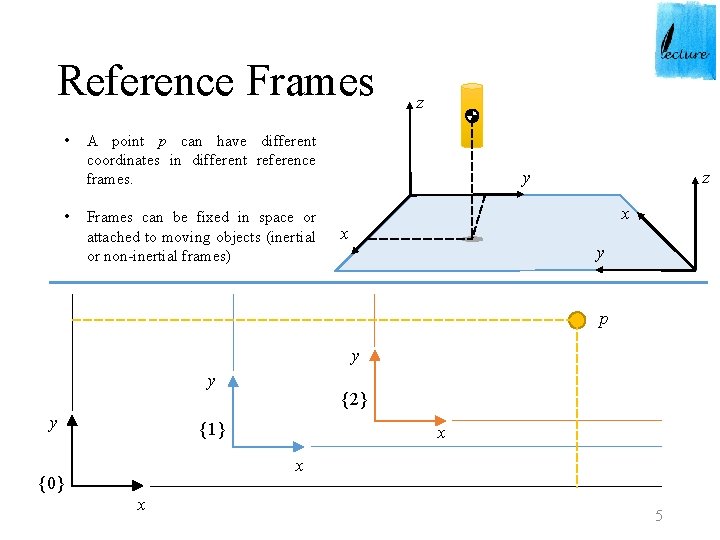
Reference Frames • • z A point p can have different coordinates in different reference frames. Frames can be fixed in space or attached to moving objects (inertial or non-inertial frames) y z x x y p y y y {2} {1} x x {0} x 5

Rotation Matrix • A 2 D example y y x p θ {2} x {1} 6

Rotation Matrix • A 2 D example y y x p θ {2} x {1} 7

Rotation Matrix (Direction Cosines) • 8

Standard Axis Rotations • 9

Rotation Matrix Identities • 10

Rotation Matrix Identities • 11

Rotation Matrix Identities • 12

Rotation Matrix Identities • 13

Rotation Matrix Identities • n is space dimension 14

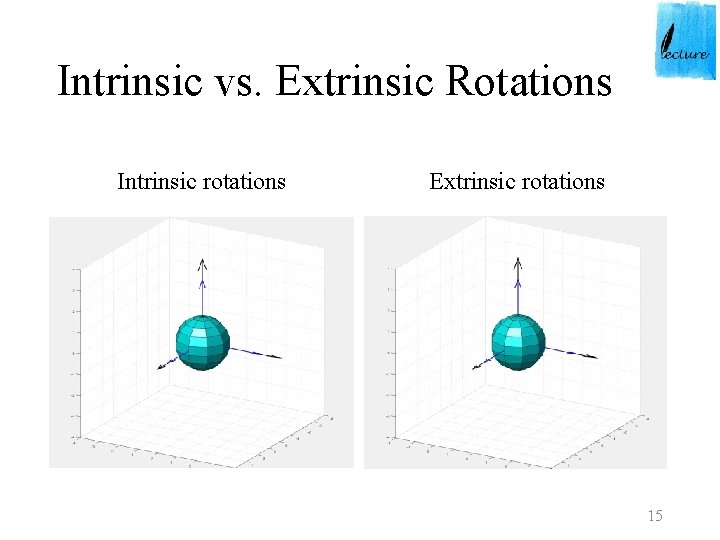
Intrinsic vs. Extrinsic Rotations Intrinsic rotations Extrinsic rotations 15

Euler Angles Leonhard Euler April 15, 1707, Basel, Switzerland September 18, 1783, Saint Petersburg, Russia 16

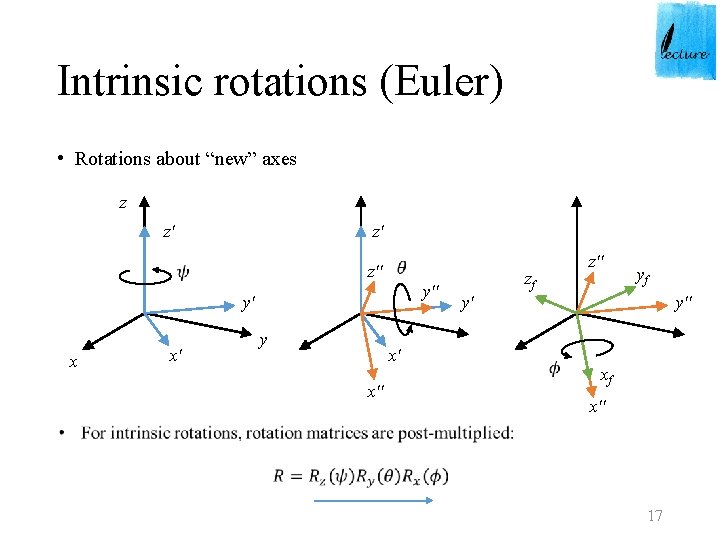
Intrinsic rotations (Euler) • Rotations about “new” axes z z' z' z'' y' x x' y x' x'' y'' zf yf y'' y' xf x'' 17

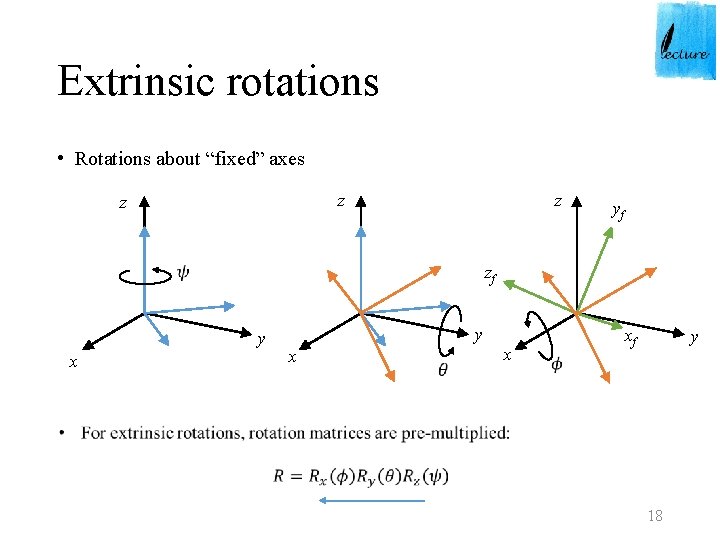
Extrinsic rotations • Rotations about “fixed” axes z zf y x yf y x x xf y 18

More on Rotation Matrix • 19

Euler Angles • Proper Euler angles: z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y • Tait-Bryan angles: x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z 20

z-y-x Euler Angles • 21

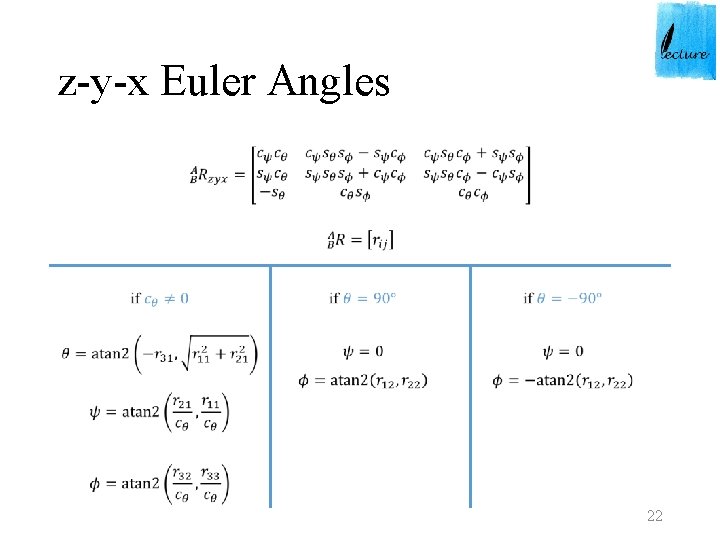
z-y-x Euler Angles • 22

Rotations in Constrained Objects • y x y {2} y x {1} x {0} 23

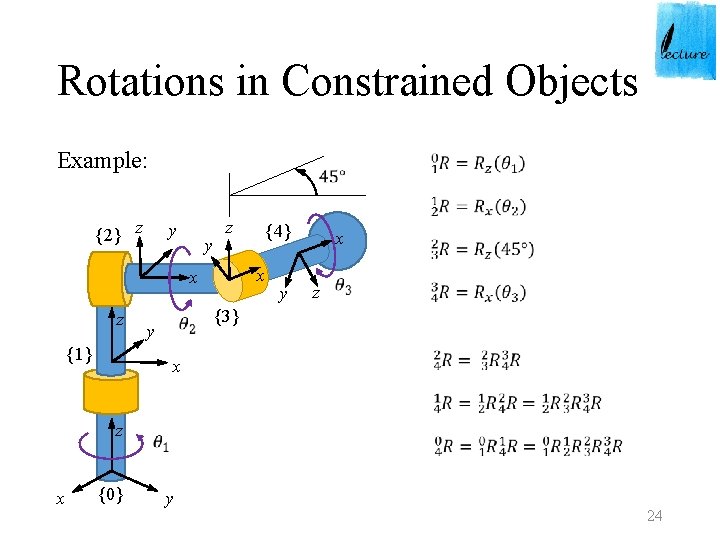
Rotations in Constrained Objects Example: {2} z y y y {1} x z {4} x x z y x z {3} z x {0} y 24

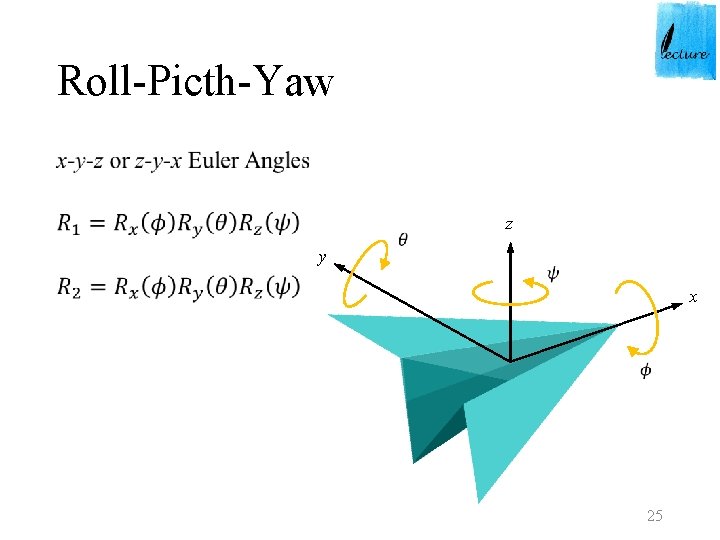
Roll-Picth-Yaw • y z x 25

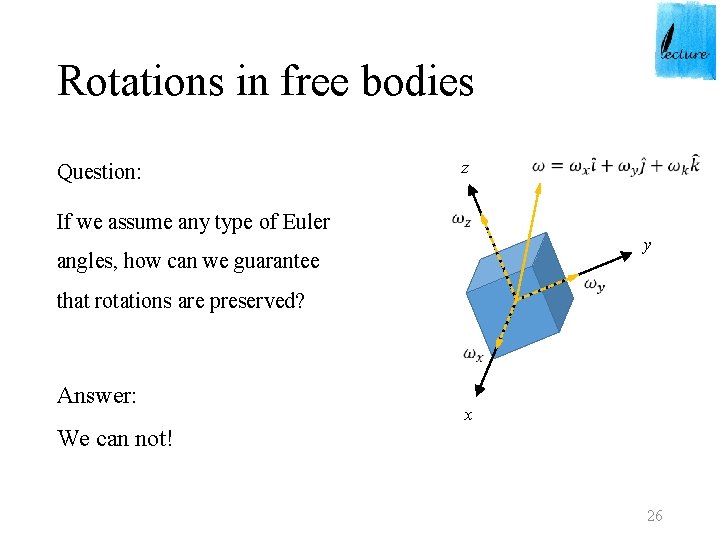
Rotations in free bodies z Question: If we assume any type of Euler y angles, how can we guarantee that rotations are preserved? Answer: x We can not! 26

Rotations in free bodies z z' z' y'' z'' y' x x' y x' x'' zf yf y'' y' xf • 27

Singularity! • Singularities at: 28

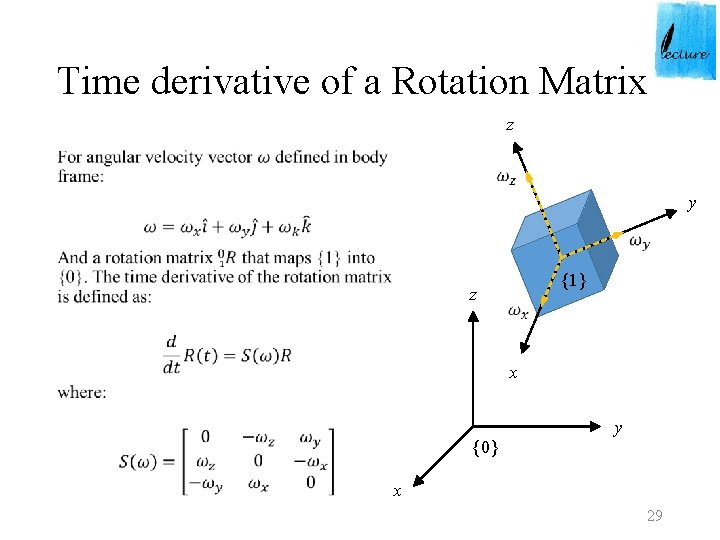
Time derivative of a Rotation Matrix z • y z {1} x {0} y x 29

Quaternion Sir William Rowan Hamilton August 4, 1805, Dublin, Republic of Ireland September 2, 1865, Dublin, Republic of Ireland 30

Quaternion Broom Bridge Dublin, Irland 31

End of Session 1 of 2 To be continued… 32

References: A good reference on Rotation matrices and some of the underlying theories is presented in chapter 2 of: § Craig, John J. “Introduction to robotics: mechanics and control. ” Vol. 3. Upper Saddle River: Pearson Prentice Hall, 2005. Proof of the time derivative of a rotation matrix: § Hamano, Fumio. “Derivative of Rotation Matrix Direct Matrix Derivation of Well Known Formula. ” ar. Xiv preprint ar. Xiv: 1311. 6010 (2013). 33