Rotation and Orientation Fundamentals Jehee Lee Seoul National

Rotation and Orientation: Fundamentals Jehee Lee Seoul National University

What is Rotation ? • Not intuitive – Formal definitions are also confusing • Many different ways to describe – – – Rotation (direction cosine) matrix Euler angles Axis-angle Rotation vector Helical angles Unit quaternions

Orientation vs. Rotation • Rotation – Circular movement • Orientation – The state of being oriented – Given a coordinate system, the orientation of an object can be represented as a rotation from a reference pose

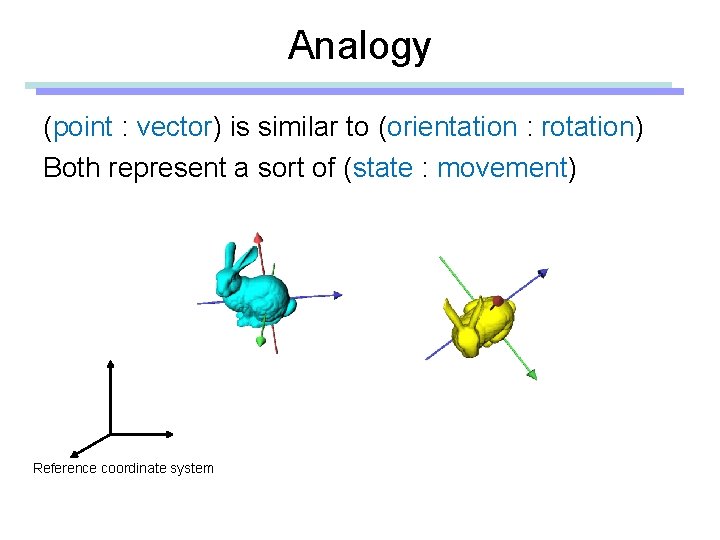
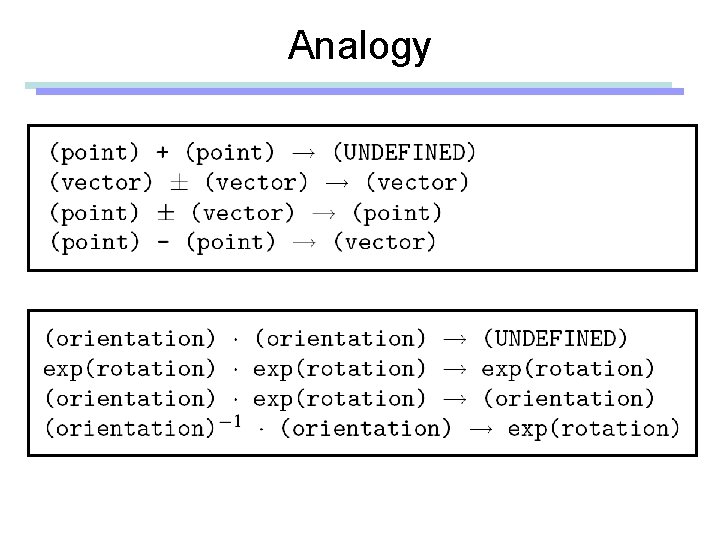
Analogy (point : vector) is similar to (orientation : rotation) Both represent a sort of (state : movement) Reference coordinate system

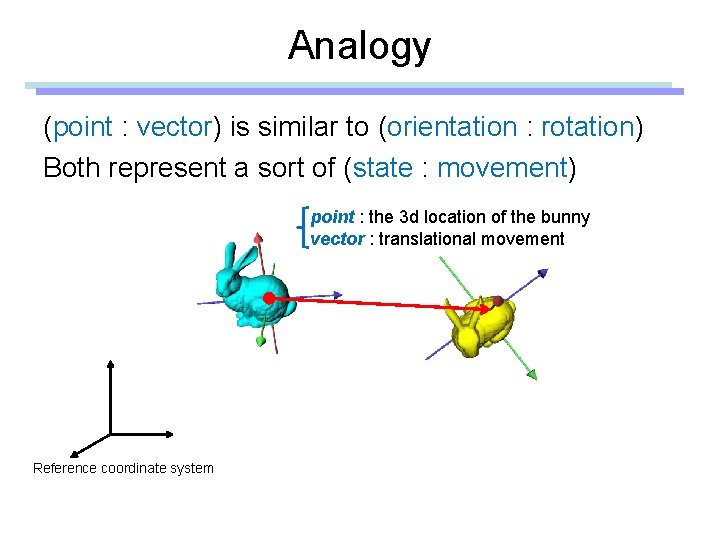
Analogy (point : vector) is similar to (orientation : rotation) Both represent a sort of (state : movement) point : the 3 d location of the bunny vector : translational movement Reference coordinate system

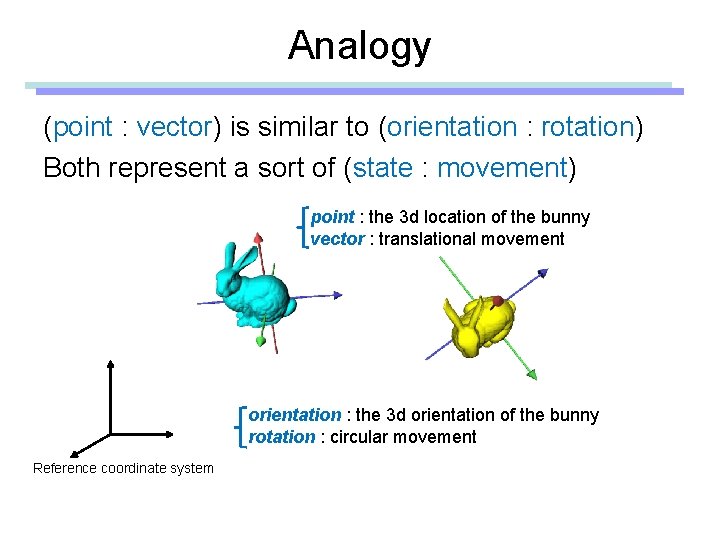
Analogy (point : vector) is similar to (orientation : rotation) Both represent a sort of (state : movement) point : the 3 d location of the bunny vector : translational movement orientation : the 3 d orientation of the bunny rotation : circular movement Reference coordinate system

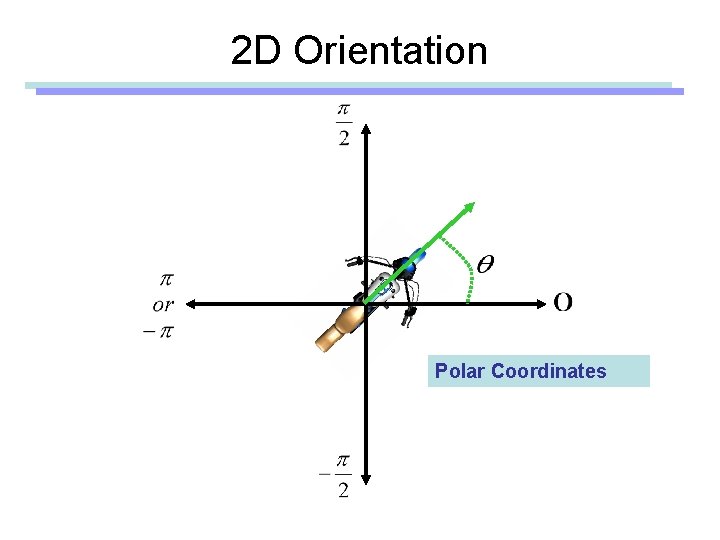
2 D Orientation Polar Coordinates

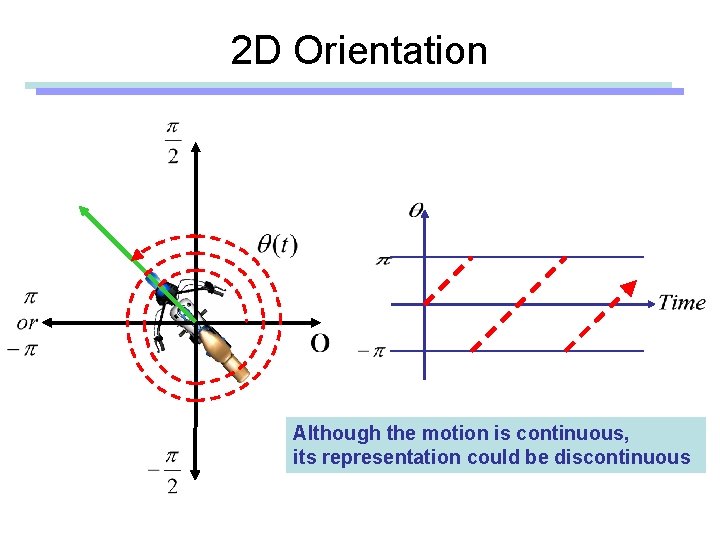
2 D Orientation Although the motion is continuous, its representation could be discontinuous

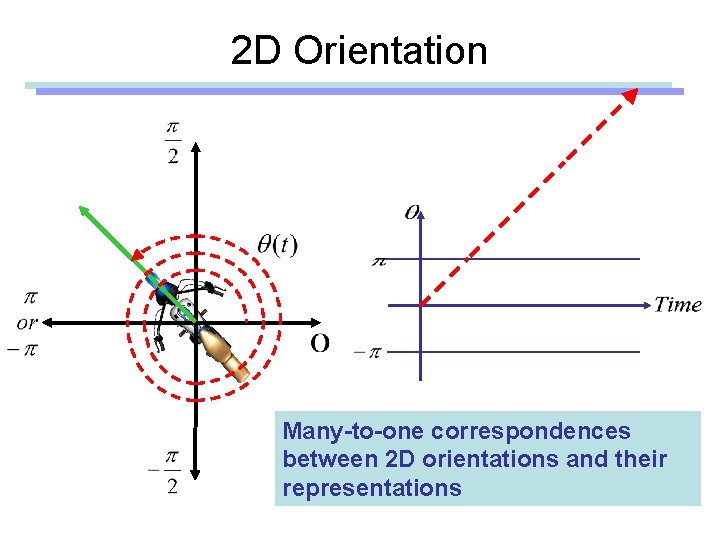
2 D Orientation Many-to-one correspondences between 2 D orientations and their representations

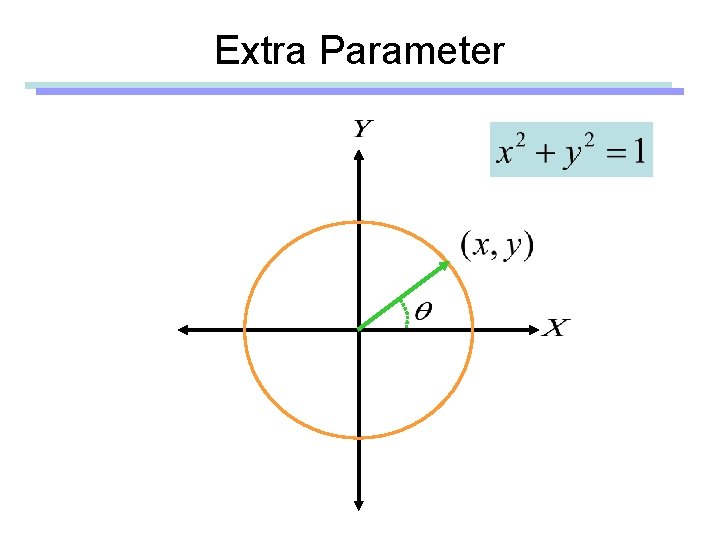
Extra Parameter

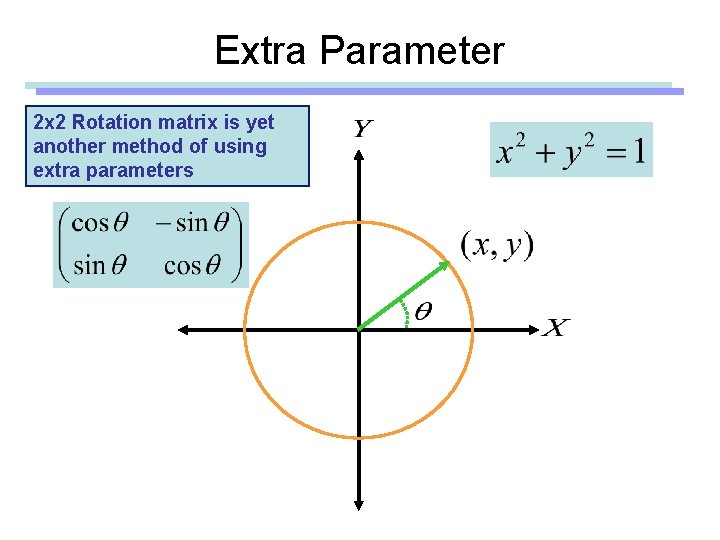
Extra Parameter 2 x 2 Rotation matrix is yet another method of using extra parameters

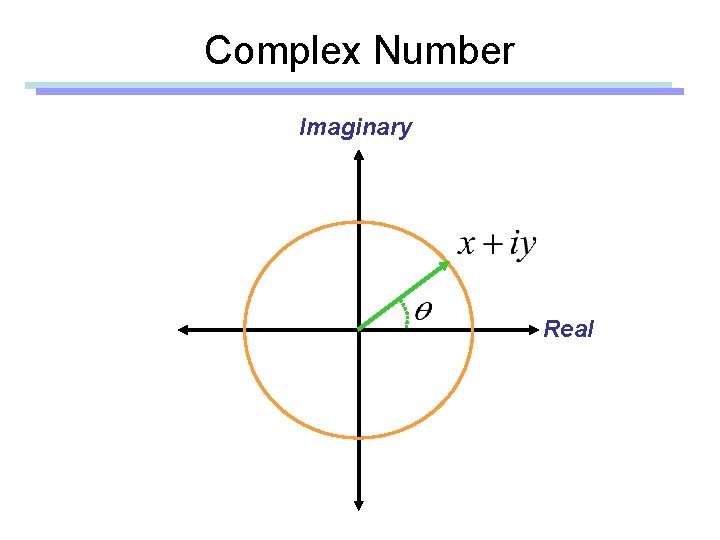
Complex Number Imaginary Real

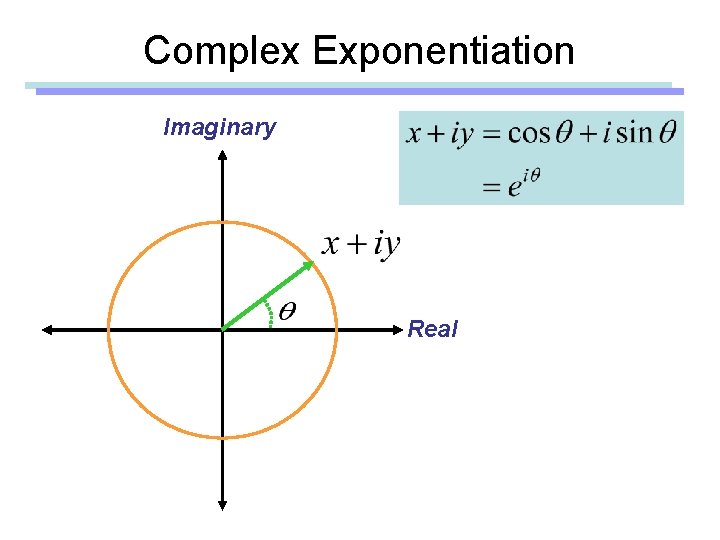
Complex Exponentiation Imaginary Real

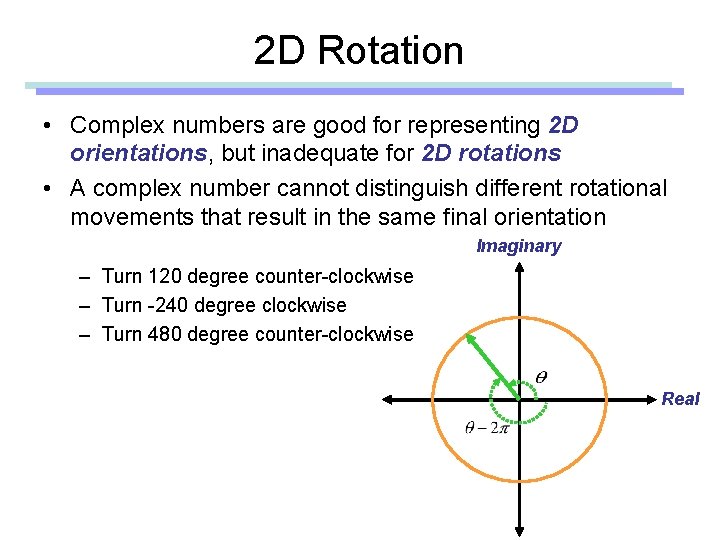
2 D Rotation • Complex numbers are good for representing 2 D orientations, but inadequate for 2 D rotations • A complex number cannot distinguish different rotational movements that result in the same final orientation Imaginary – Turn 120 degree counter-clockwise – Turn -240 degree clockwise – Turn 480 degree counter-clockwise Real

2 D Rotation and Orientation • 2 D Rotation – The consequence of any 2 D rotational movement can be uniquely represented by a turning angle • 2 D Orientation – The non-singular parameterization of 2 D orientations requires extra parameters • Eg) Complex numbers, 2 x 2 rotation matrices

Operations in 2 D • (orientation) : complex number • (rotation) : scalar value • exp(rotation) : complex number

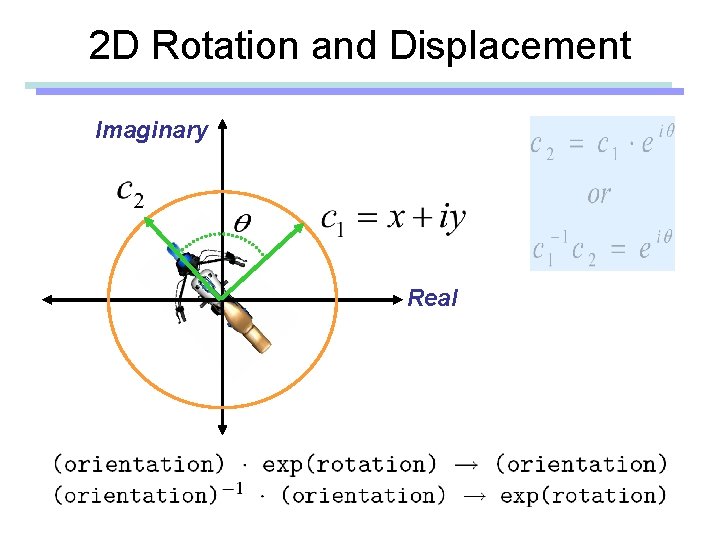
2 D Rotation and Displacement Imaginary Real

2 D Rotation and Displacement Imaginary Real

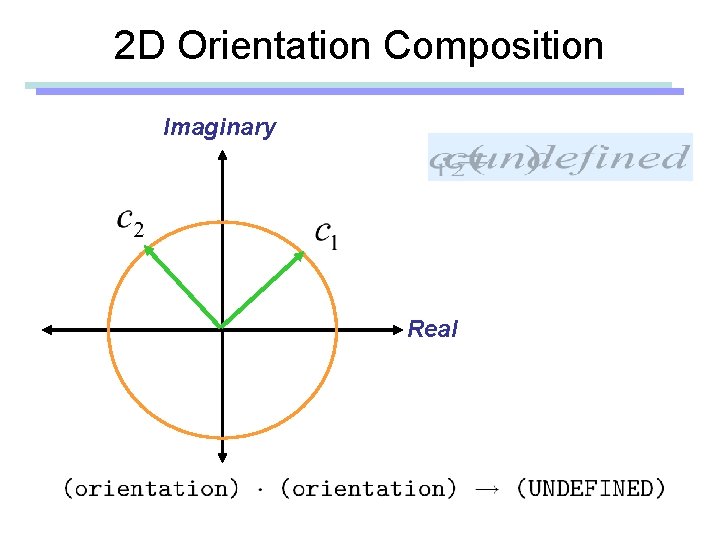
2 D Orientation Composition Imaginary Real

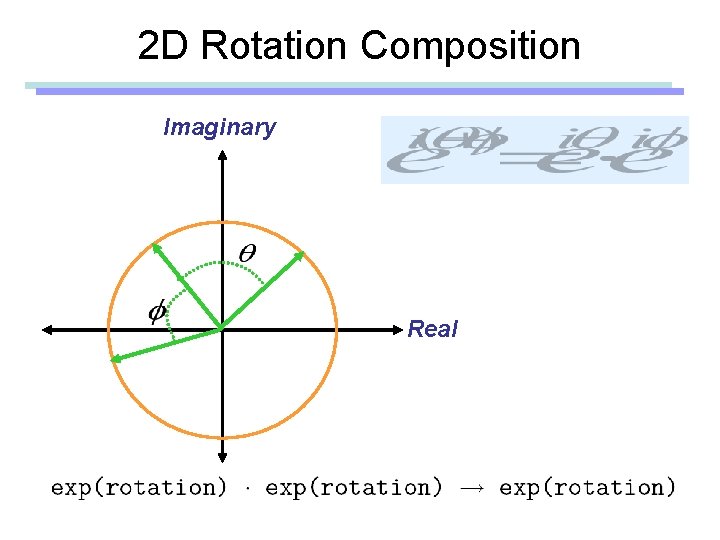
2 D Rotation Composition Imaginary Real

Analogy

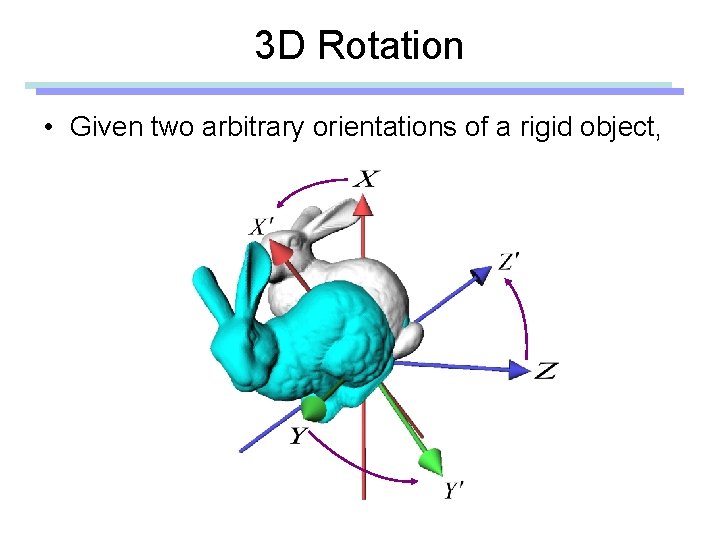
3 D Rotation • Given two arbitrary orientations of a rigid object,

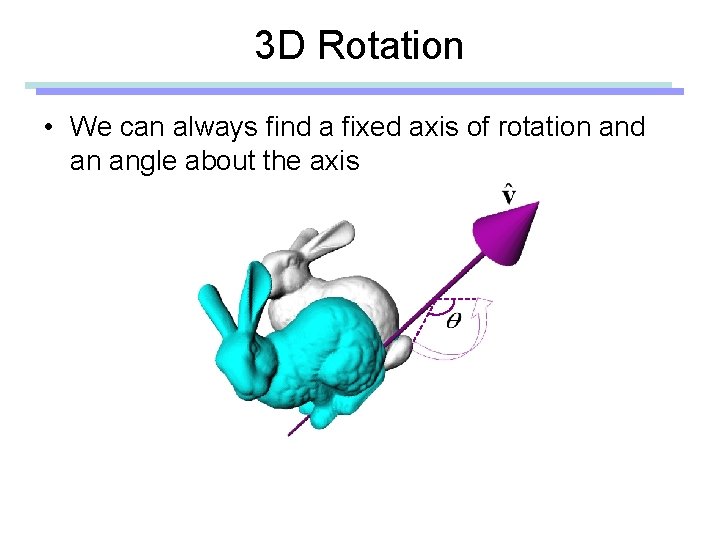
3 D Rotation • We can always find a fixed axis of rotation and an angle about the axis

Euler’s Rotation Theorem The general displacement of a rigid body with one point fixed is a rotation about some axis Leonhard Euler (1707 -1783) In other words, • Arbitrary 3 D rotation equals to one rotation around an axis • Any 3 D rotation leaves one vector unchanged

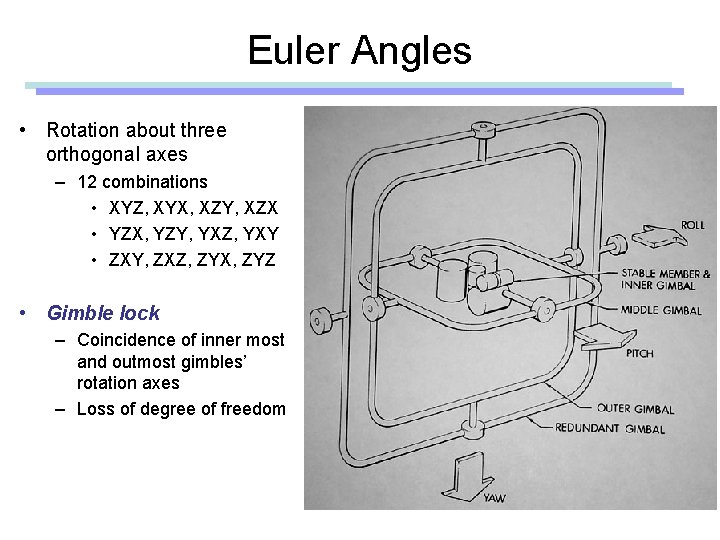
Euler angles • Gimble – Hardware implementation of Euler angles – Aircraft, Camera

Euler Angles • Rotation about three orthogonal axes – 12 combinations • XYZ, XYX, XZY, XZX • YZX, YZY, YXZ, YXY • ZXY, ZXZ, ZYX, ZYZ • Gimble lock – Coincidence of inner most and outmost gimbles’ rotation axes – Loss of degree of freedom

Euler Angles • Euler angles are ambiguous – Two different Euler angles can represent the same orientation – This ambiguity brings unexpected results of animation where frames are generated by interpolation.

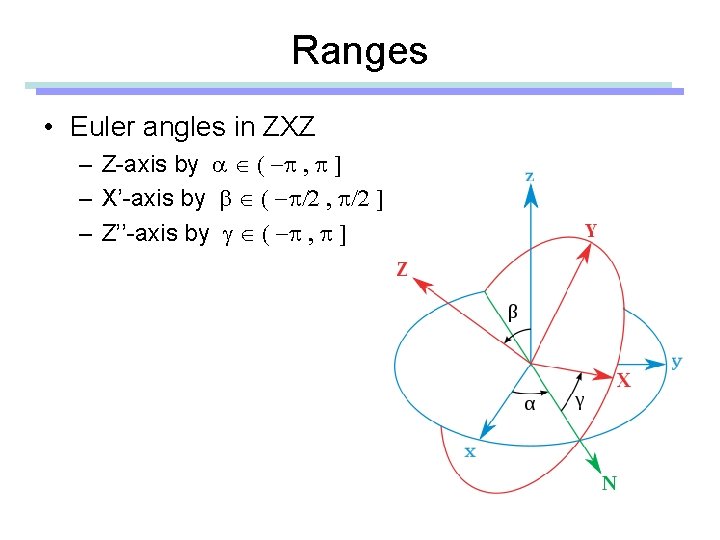
Ranges • Euler angles in ZXZ – Z-axis by a ( -p , p ] – X’-axis by b ( -p/2 , p/2 ] – Z’’-axis by g ( -p , p ]

Dependence • Compare – Rotation about z-axis by 180 degree – Rotation about y-axis by 180 degree, followed by another rotation about x-axis by 180 degree • Rotations about x-, y-, and z-axes are dependent

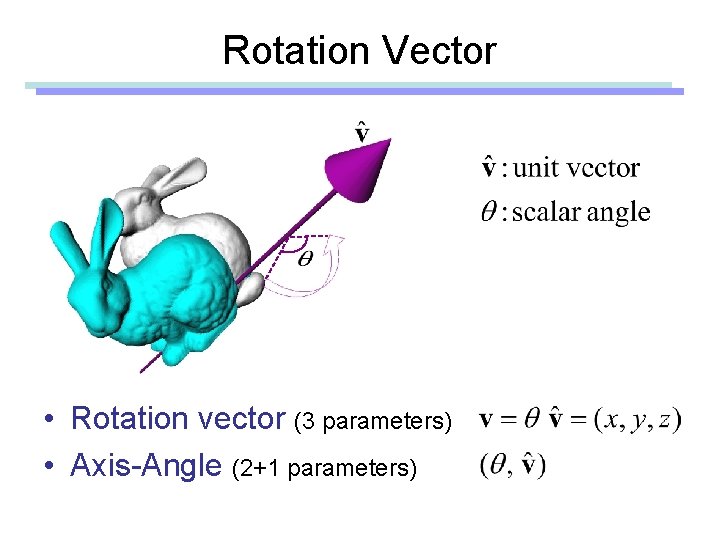
Rotation Vector • Rotation vector (3 parameters) • Axis-Angle (2+1 parameters)

3 D Orientation • Unhappy with three parameters – Euler angles • Discontinuity (or many-to-one correspondences) • Gimble lock – Rotation vector (a. k. a Axis/Angle) • Discontinuity (or many-to-one correspondences)

Using an Extra Parameter • Euler parameters

Quaternions • William Rowan Hamilton (1805 -1865) – Algebraic couples (complex number) 1833 where

Quaternions • William Rowan Hamilton (1805 -1865) – Algebraic couples (complex number) 1833 where – Quaternions 1843 where

Quaternions William Thomson “… though beautifully ingenious, have been an unmixed evil to those who have touched them in any way. ” Arthur Cayley “… which contained everything but had to be unfolded into another form before it could be understood. ”

Unit Quaternions • Unit quaternions represent 3 D rotations

Rotation about an Arbitrary Axis • Rotation about axis by angle where Purely Imaginary Quaternion

Unit Quaternion Algebra • Identity • Multiplication • Inverse – Opposite axis or negative angle • Unit quaternion space is – closed under multiplication and inverse, – but not closed under addition and subtraction

Unit Quaternion Algebra • Antipodal equivalence – q and –q represent the same rotation – ex) rotation by p-q about opposite direction – 2 -to-1 mapping between S 3 and SO(3) – Twice as fast as in SO(3)

3 D Orientations and Rotations Orientations and rotations are different in coordinate-invariant geometric programming Use unit quaternions for orientation representation – 3 x 3 orthogonal matrix is theoretically identical Use 3 -vectors for rotation representation

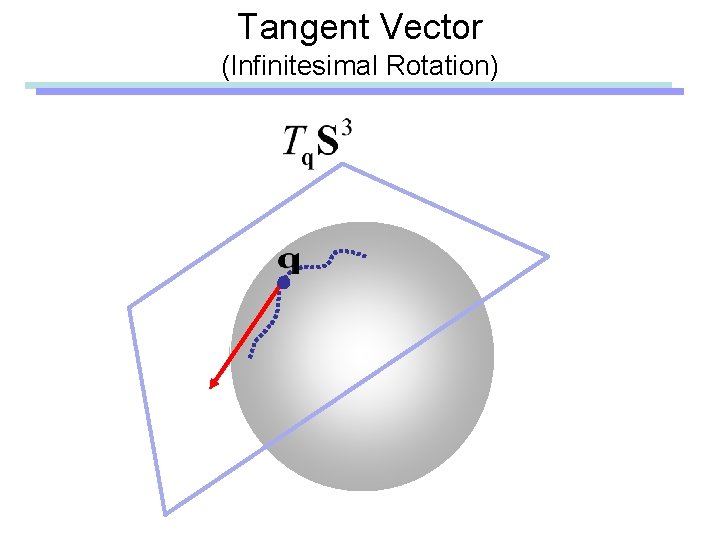
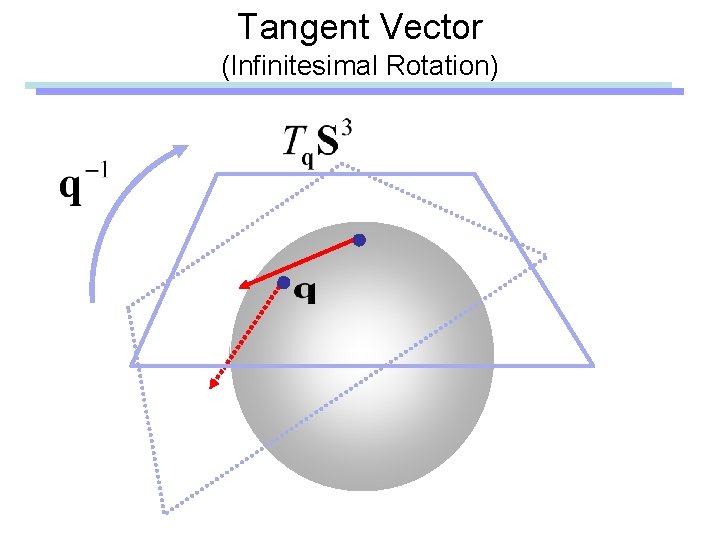
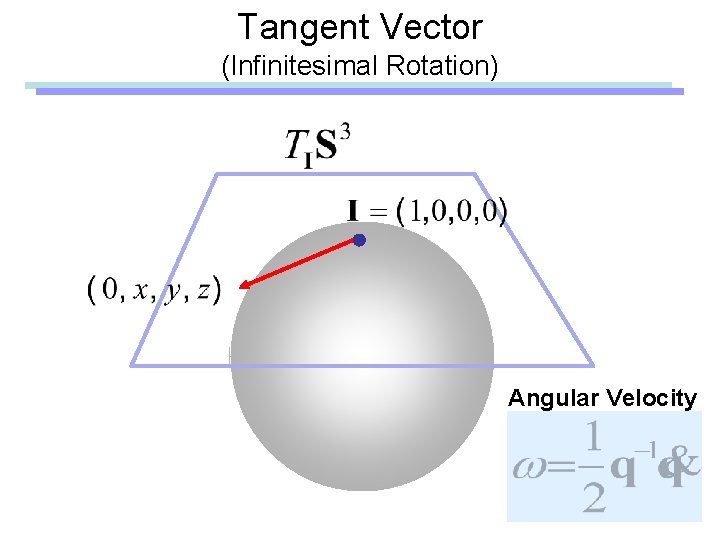
Tangent Vector (Infinitesimal Rotation)

Tangent Vector (Infinitesimal Rotation)

Tangent Vector (Infinitesimal Rotation) Angular Velocity

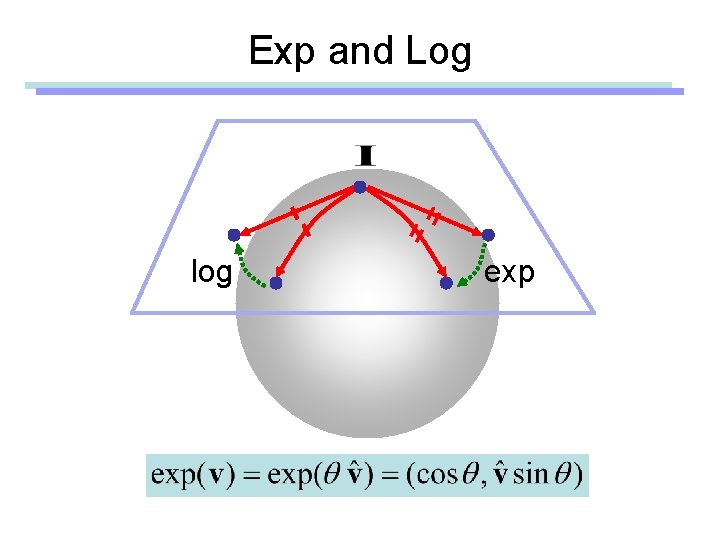
Exp and Log log exp

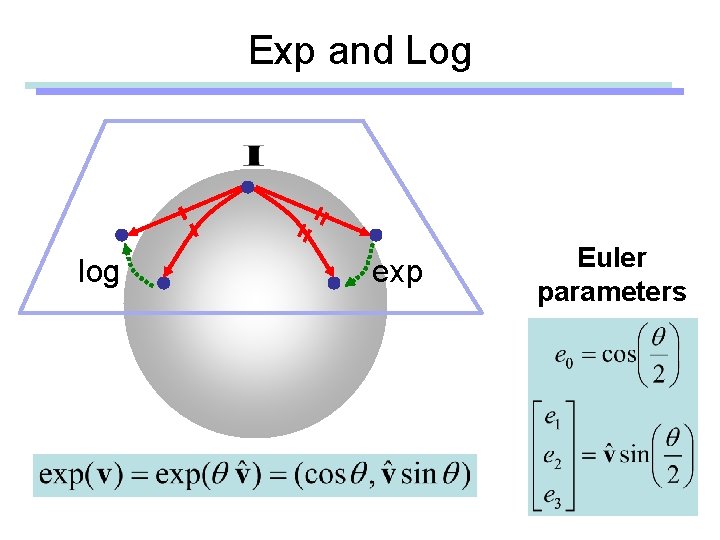
Exp and Log log exp Euler parameters

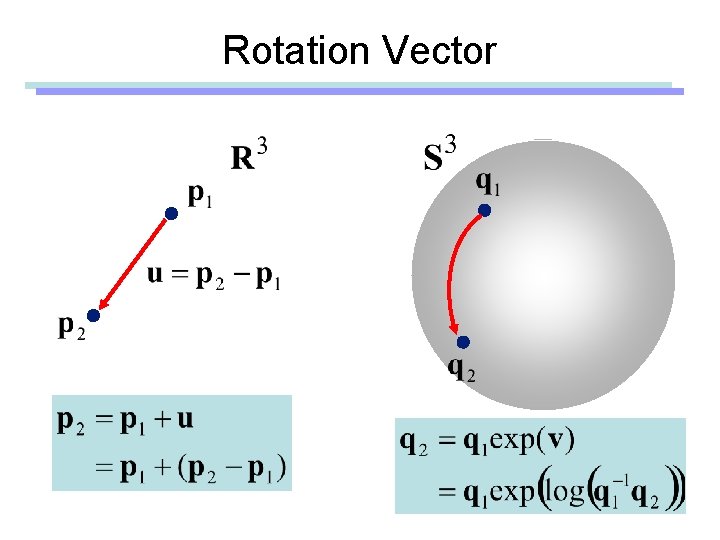
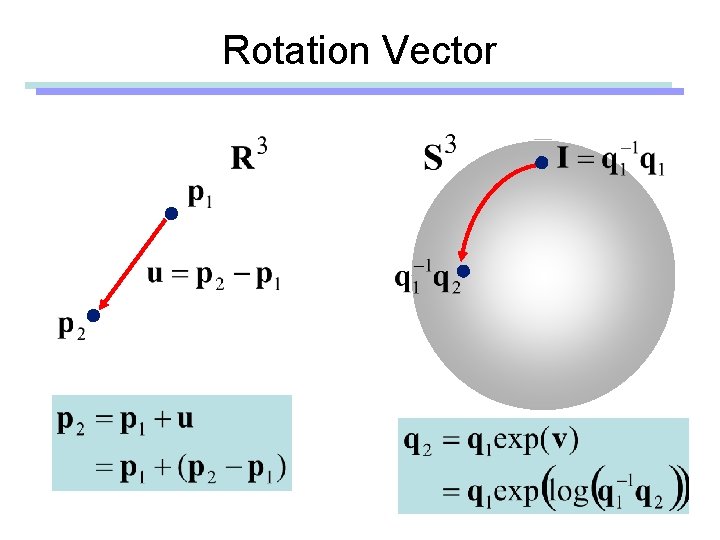
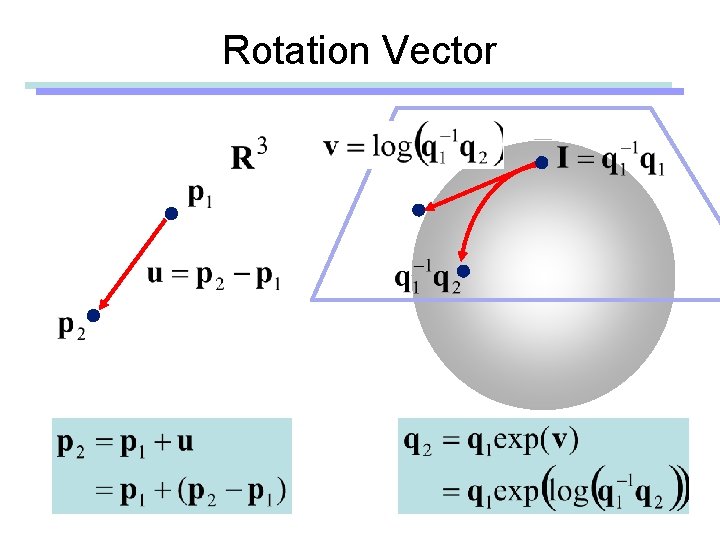
Rotation Vector

Rotation Vector

Rotation Vector

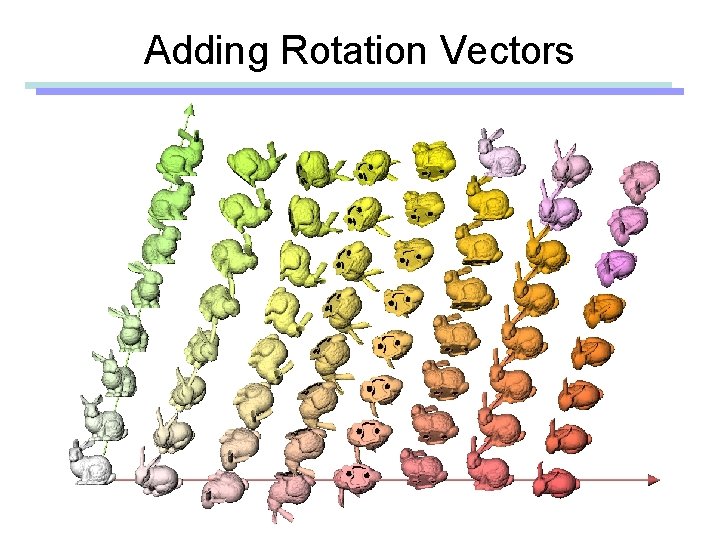
Rotation Vector • Finite rotation – Eg) Angular displacement – Be careful when you add two rotation vectors • Infinitesimal rotation – Eg) Instantaneous angular velocity – Addition of angular velocity vectors are meaningful

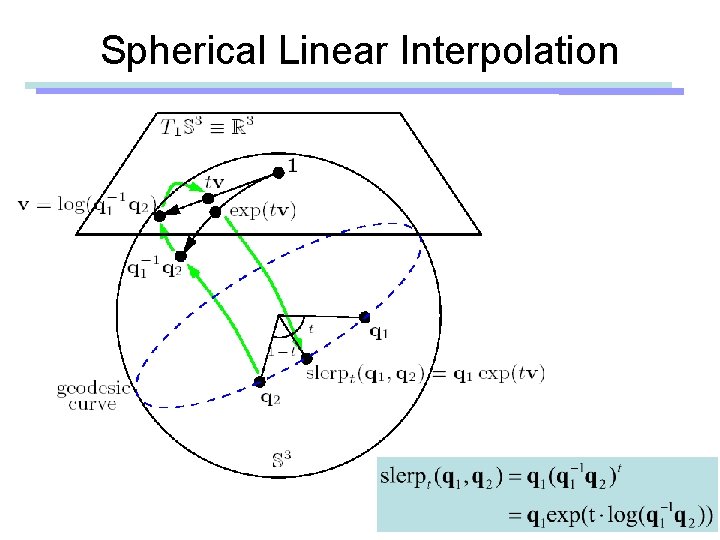
Spherical Linear Interpolation • SLERP [Shoemake 1985] – Linear interpolation of two orientations

Spherical Linear Interpolation

Coordinate-Invariant Operations

Adding Rotation Vectors

Affine Combination of Orientations

Analogy • (point : vector) is similar to (orientation : rotation)

Rotation Matrix vs. Unit Quaternion • Equivalent in many aspects – Redundant, No singularity – Exp & Log, Special tangent space • Why quaternions ? – Fewer parameters, Simpler algebra – Easy to fix numerical error • Cf) matrix orthogonalization (Gram-shmidt process, QR, SVD decomposition) • Why rotation matrices ? – One-to-one correspondence – Handle rotation and translation in a uniform way • Eg) 4 x 4 homogeneous matrices

Rotation Conversions • In theory, conversion between any representations is always possible • In practice, conversion is not straightward because of difference in convention • Quaternion to Matrix