Rotating Spring n Problem A helical spring is

Rotating Spring n Problem A helical spring is rotated about one of its ends around a vertical axis. Investigate the expansion of the spring with and without an additional mass attached to its free end. 1

Overview n Experimental Setup Experimental Approach and Details n Experimental Results Statistics and Graphics n Theory The Physics Behind Rotating Spring n Comparison Matching of Theory and Results n Conclusion 2

Experimental Setup Helical Spring Vertical Axis 3

Experimental Details n Relevant Parameters n m (mass of spring): 2. 3 g n M (additional mass): 1. 0, 2. 0, 5. 0 g n (angular velocity) n lo (original length): 2. 6 cm n k (force constant): 2. 5 N/m 4

Experiment n Spring without mass 5 10 15 20 25 30 35 40 45 48 5

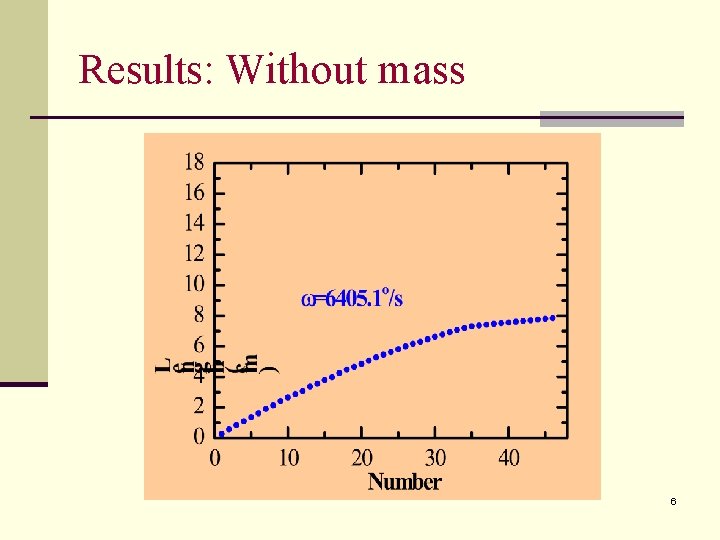
Results: Without mass 6

Experiment II n Spring with mass 5 10 15 20 25 30 35 40 45 48 7

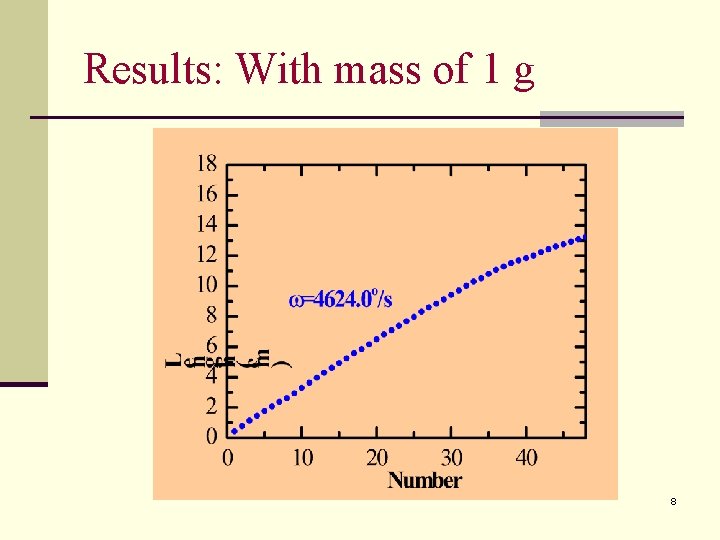
Results: With mass of 1 g 8

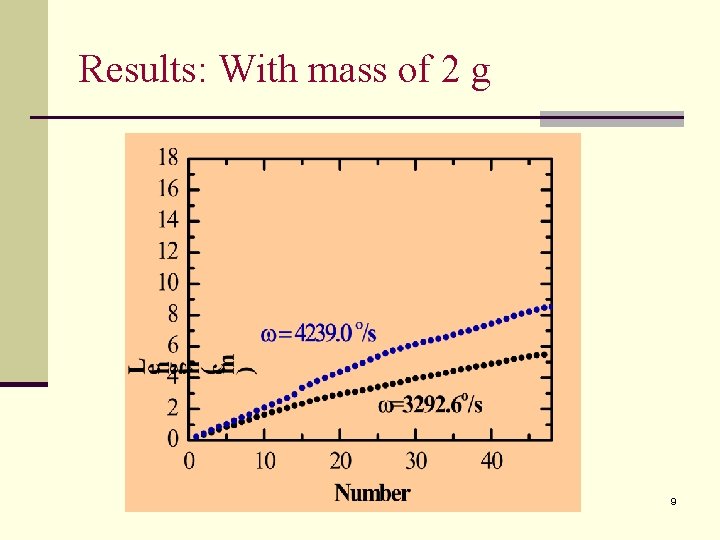
Results: With mass of 2 g 9

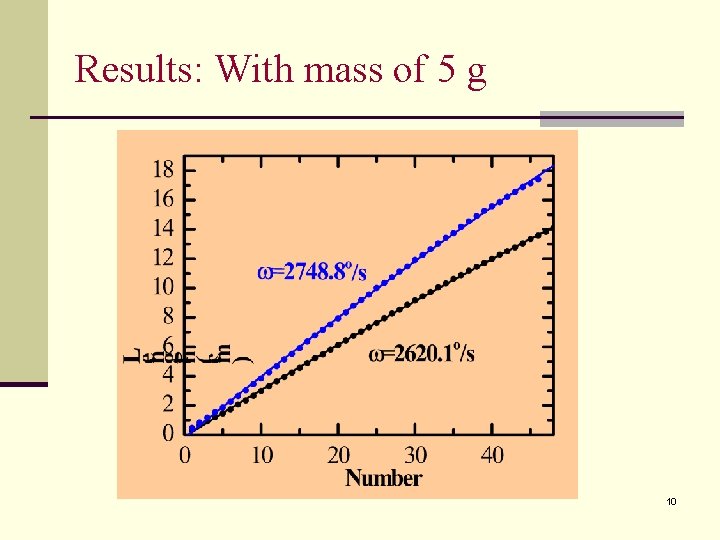
Results: With mass of 5 g 10

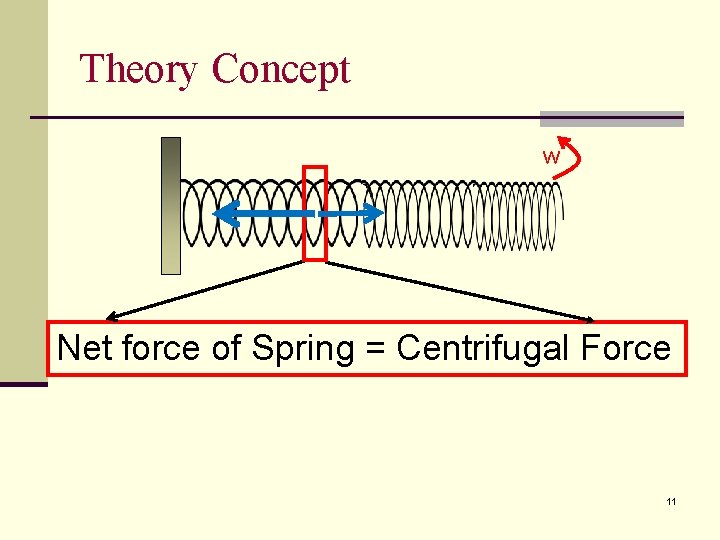
Theory Concept w Net force of Spring = Centrifugal Force 11

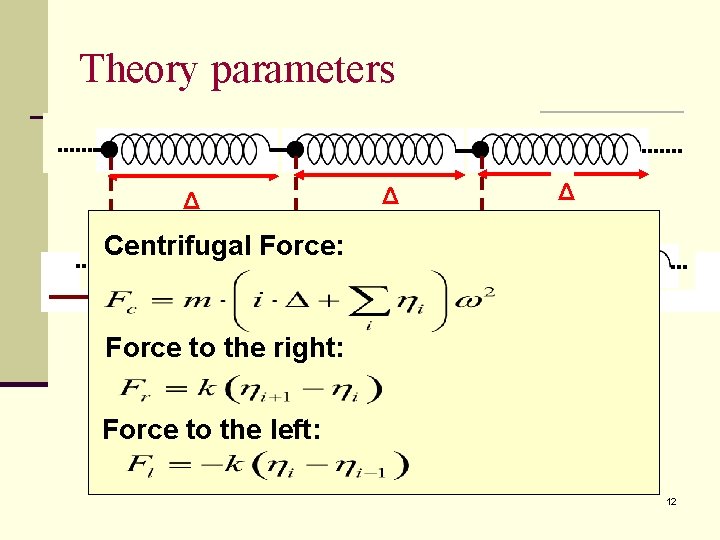
Theory parameters Δ Δ Δ Centrifugal Force: ηi-1 ηi Force to the right: ηi+1 Force to the left: 12

Theory Newton’s second law of motion in equilibrium: Continuum Limit: 13

Theory General Solution: Sinusoid formula 14

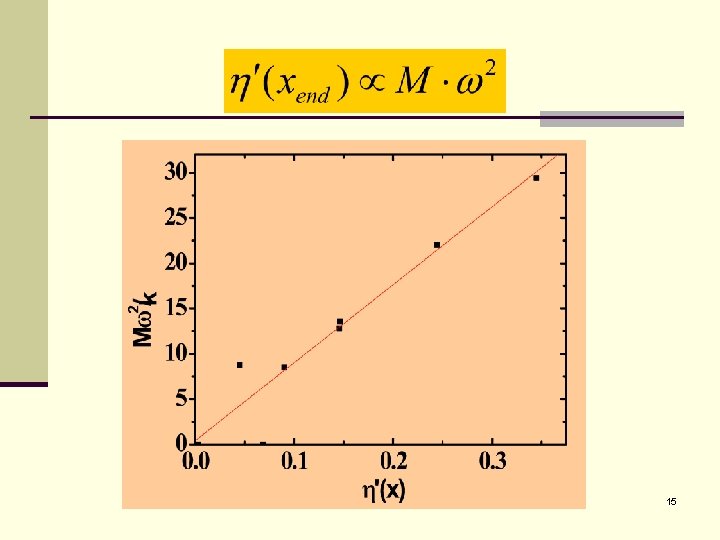
15

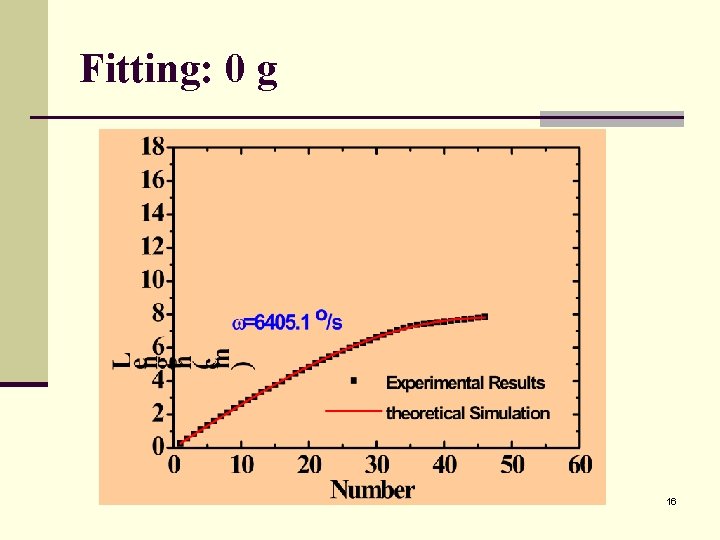
Fitting: 0 g 16

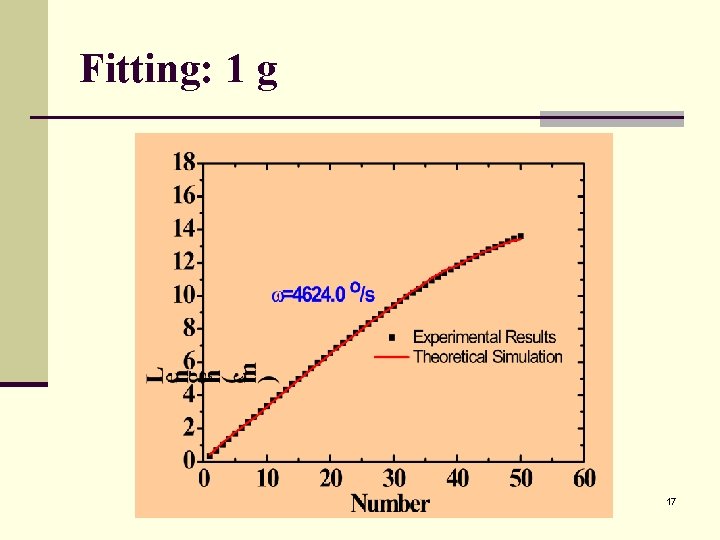
Fitting: 1 g 17

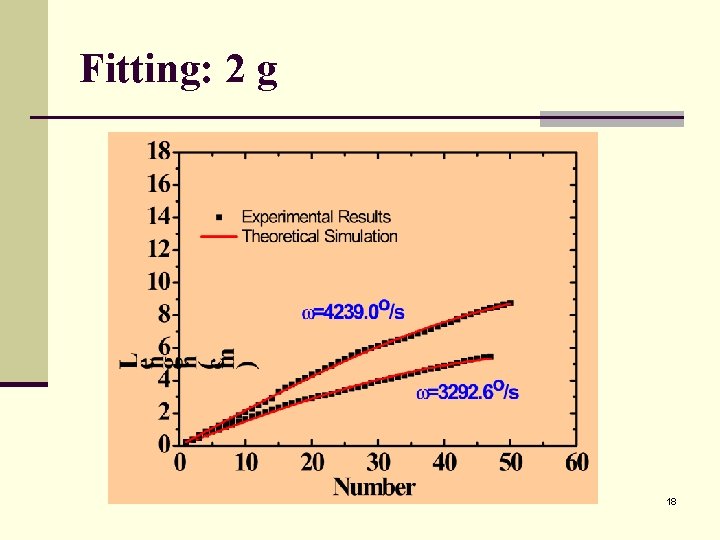
Fitting: 2 g 18

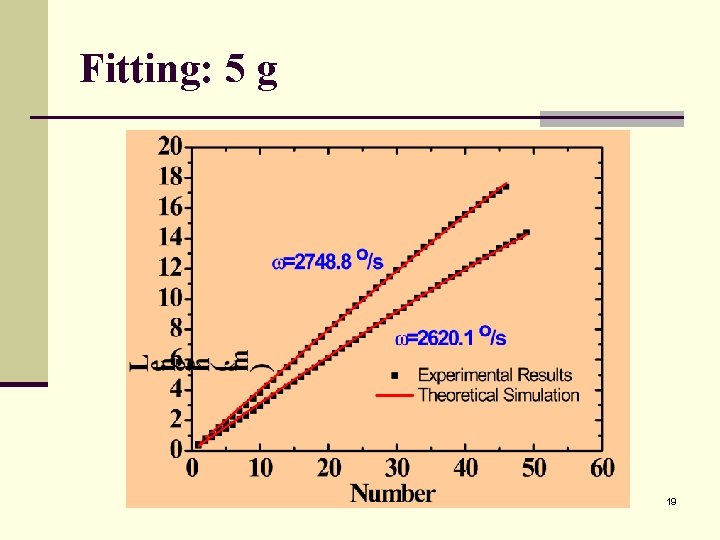
Fitting: 5 g 19

Conclusion n Without mass n Distribution of the spring is nonuniform n Denser at further end of the spring 20

Conclusion n With mass n More uniform distribution of the spring 21

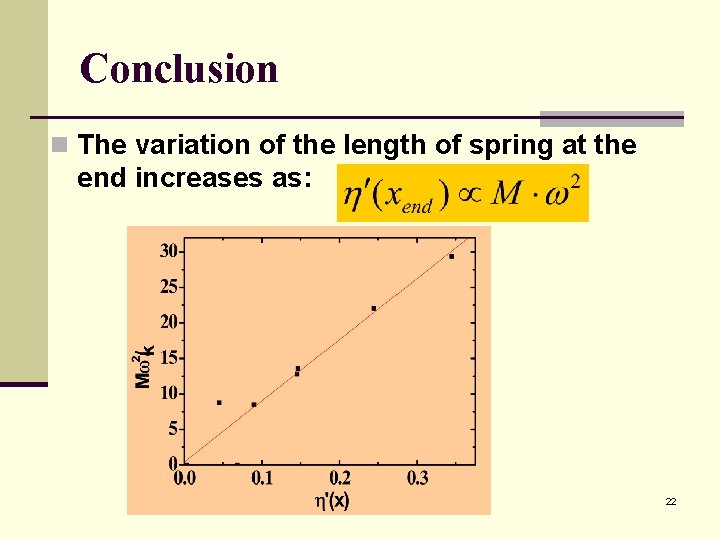
Conclusion n The variation of the length of spring at the end increases as: 22