Rotating Fluid Part II A GFD view of

Rotating Fluid -Part II A “GFD view” of the Ocean and the Atmosphere (a follow up Raymond’s Lectures) Arnaud Czaja

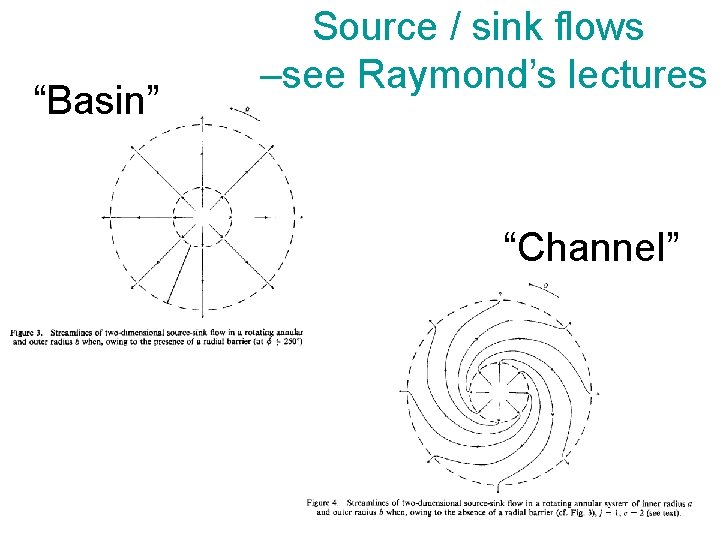
“Basin” Source / sink flows –see Raymond’s lectures “Channel”

“Basin” Source / sink flows –see Raymond’s lectures “Channel” No distinction between Ocean & Atmosphere…

Central idea • Constraint 1: Ocean & Atmosphere are rapidly rotating fluids: geostrophy is the leading order dynamics. • Constraint 2: The two fluids must transport energy poleward (cold parcels move equatorward and warm parcels poleward)

Central idea • This brings a key distinction between basins (~ocean) and channel (~atmosphere)’s geometry: Basins: walls provide d. P/dx and a large scale (eddy free) geostrophic heat transport is possible. Channels: no zonally integrated d. P/dx and the heat transport must involve eddies and / or ageostrophic effects (e. g. , Hadley cell).

Outline • The energy constraint • Basin dynamics • Channel dynamics

The energy constraint

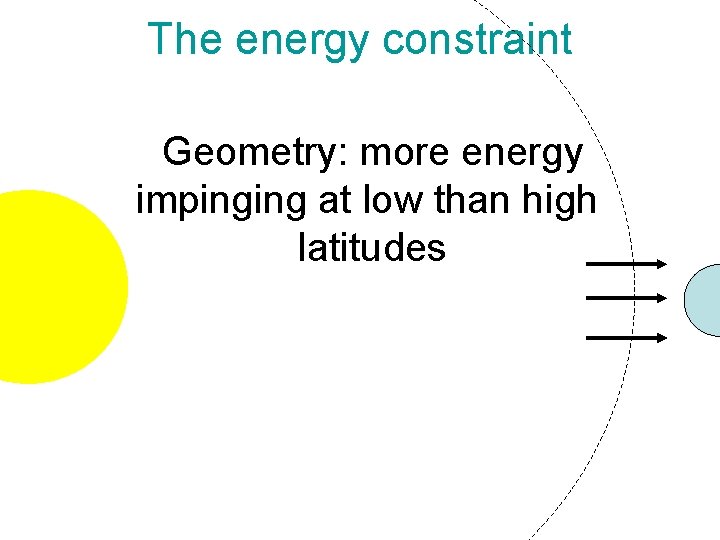
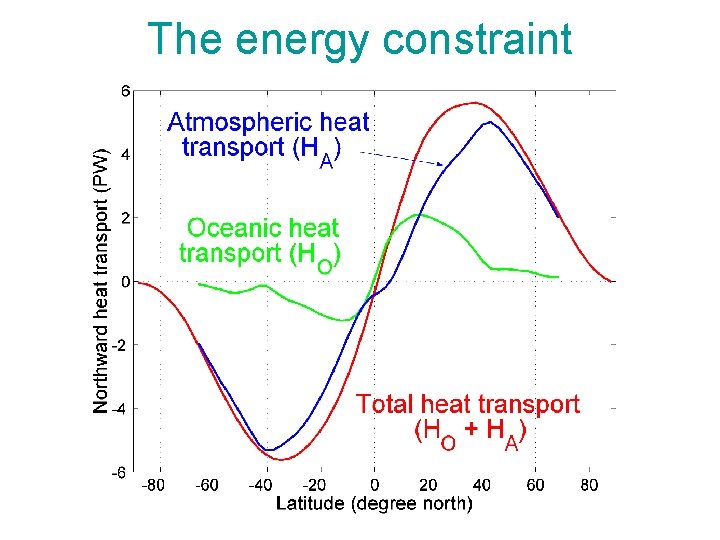
The energy constraint Geometry: more energy impinging at low than high latitudes

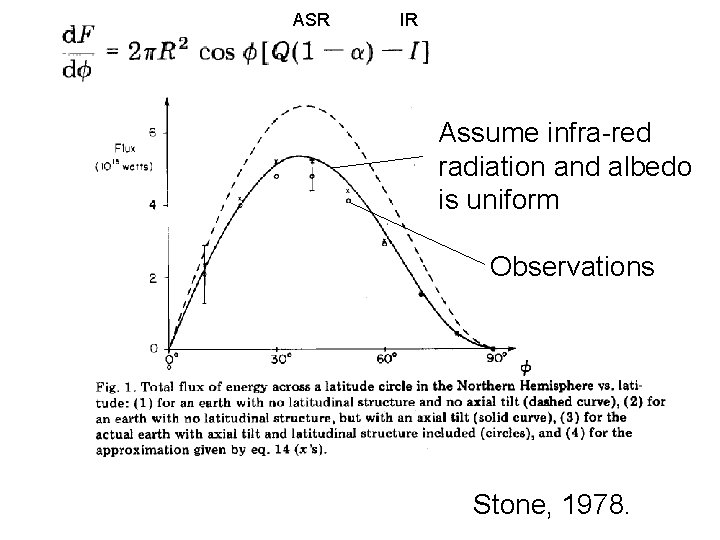
ASR IR Assume infra-red radiation and albedo is uniform Observations Stone, 1978.

The energy constraint

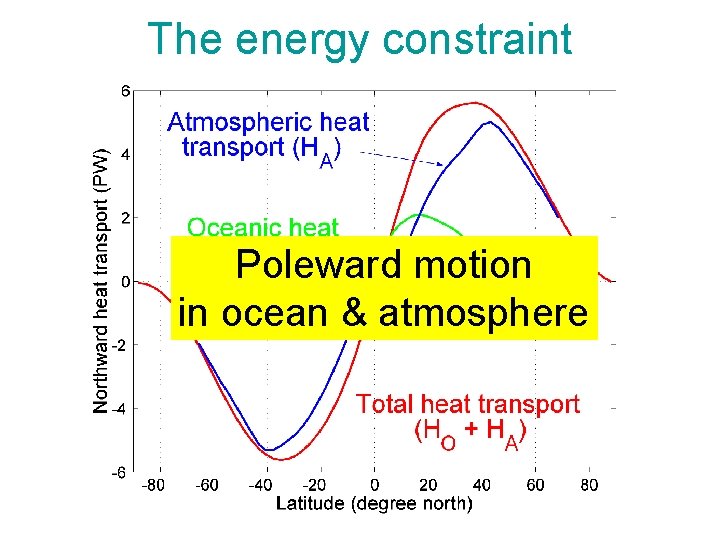
The energy constraint Poleward motion in ocean & atmosphere

Basin: Northern Oceans, Atmosphere • Background • Geostrophic mass transport calculation • Heat transport • Complications…

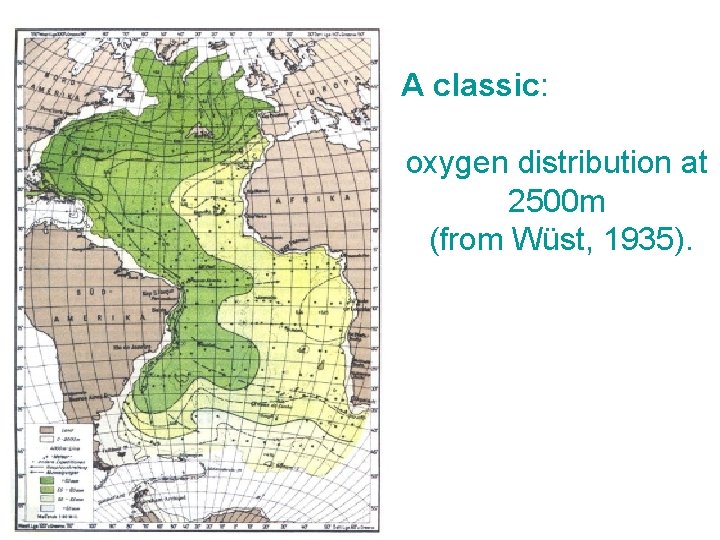
A classic: oxygen distribution at 2500 m (from Wüst, 1935).

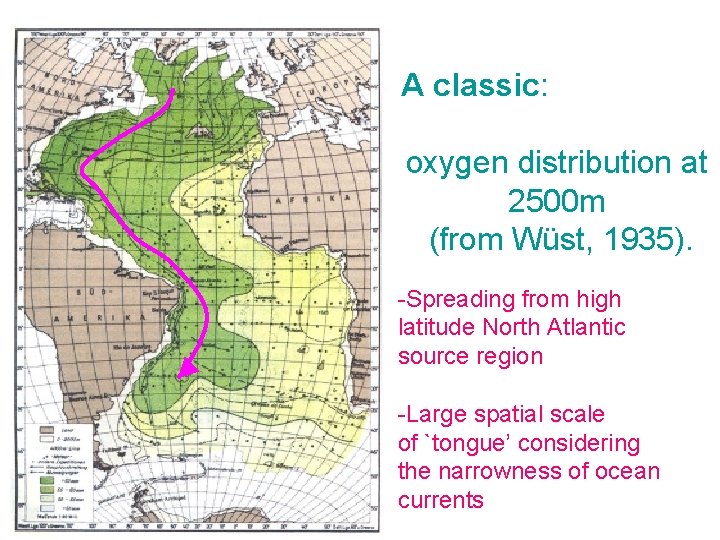
A classic: oxygen distribution at 2500 m (from Wüst, 1935). -Spreading from high latitude North Atlantic source region -Large spatial scale of `tongue’ considering the narrowness of ocean currents

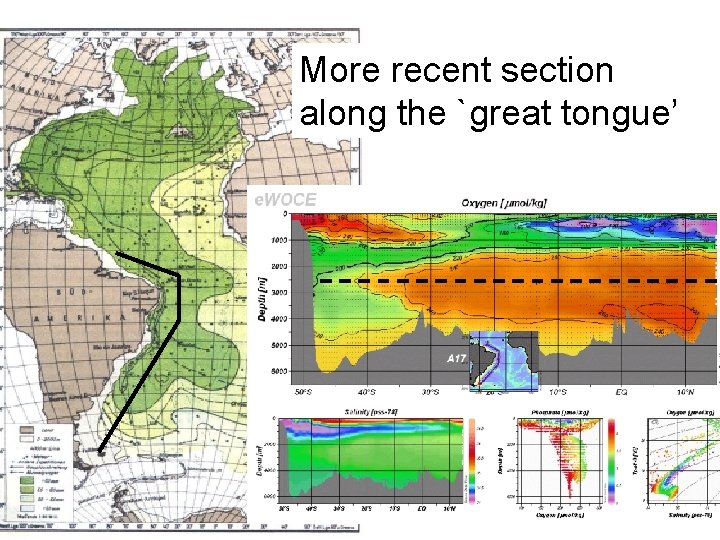
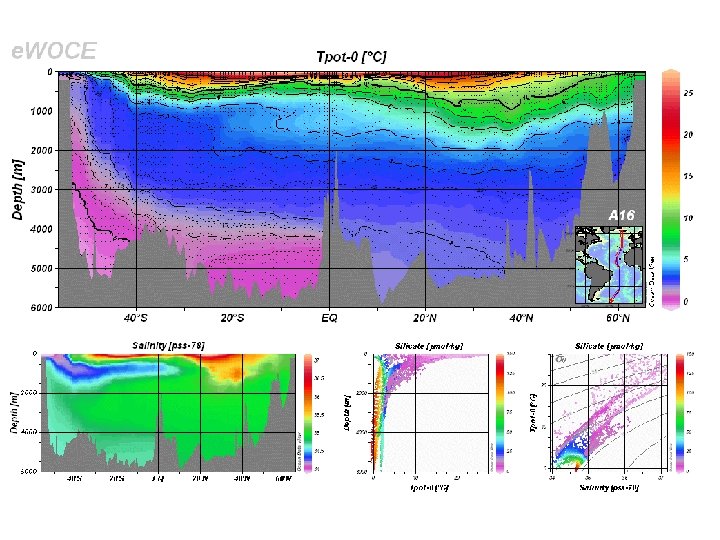
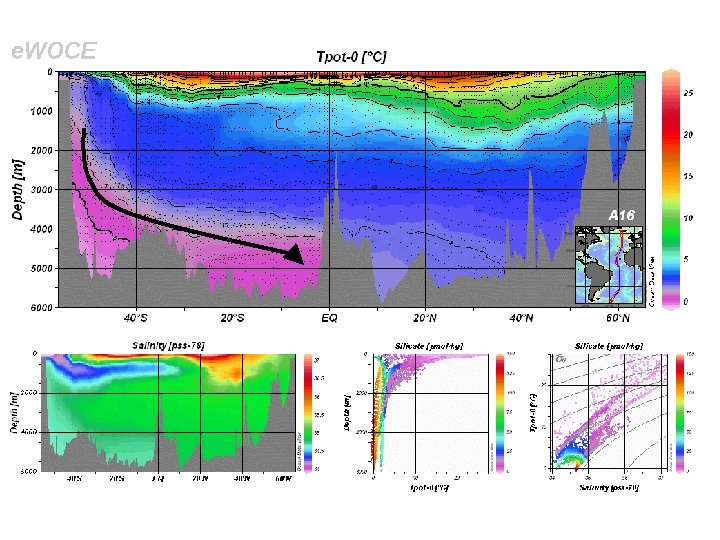
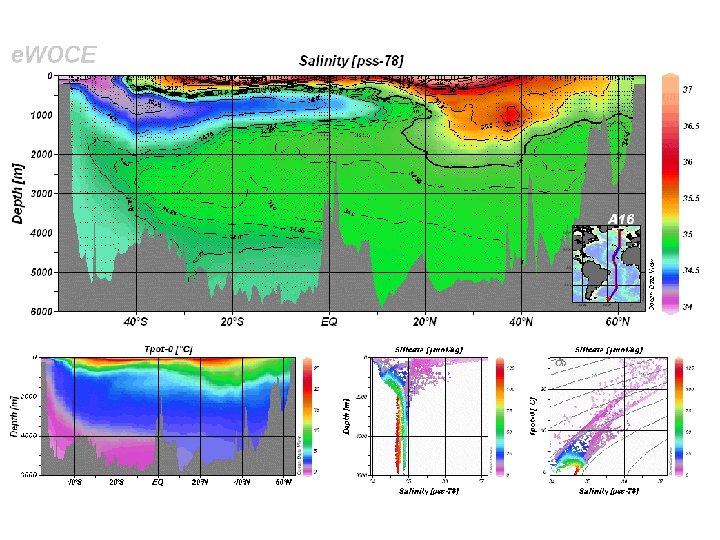
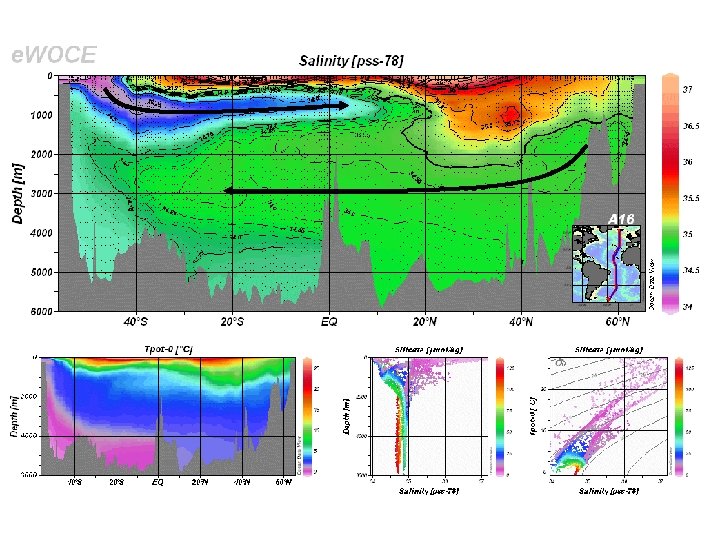
More recent section along the `great tongue’

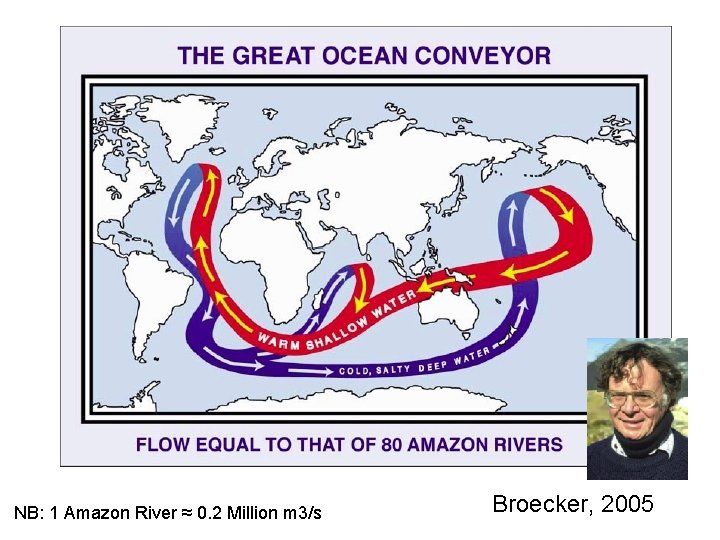
The “great oceanic conveyor belt”

The “great oceanic conveyor belt”

NB: 1 Amazon River ≈ 0. 2 Million m 3/s Broecker, 2005

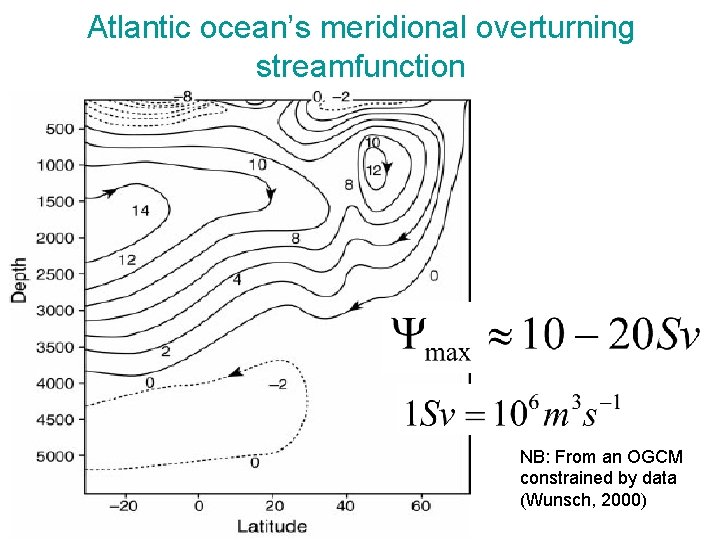
Atlantic ocean’s meridional overturning streamfunction NB: From an OGCM constrained by data (Wunsch, 2000)

Can we measure the ocean circulation in basins using the Geostrophic calculation? • All you need is thermal wind: Coriolis parameter East-west density gradient North-South velocity Gradient with height

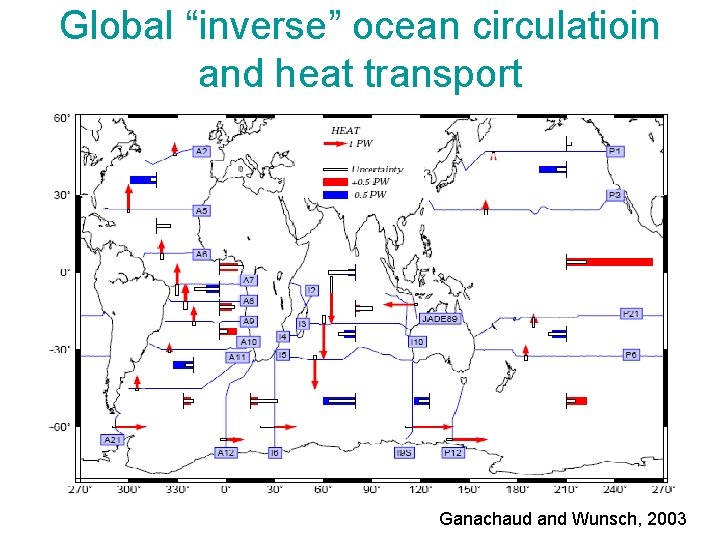
Global “inverse” ocean circulatioin and heat transport Ganachaud and Wunsch, 2003

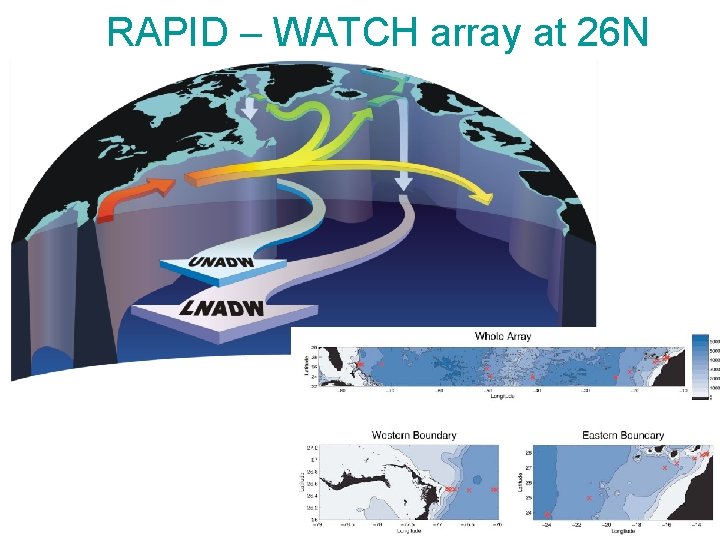
RAPID – WATCH array at 26 N

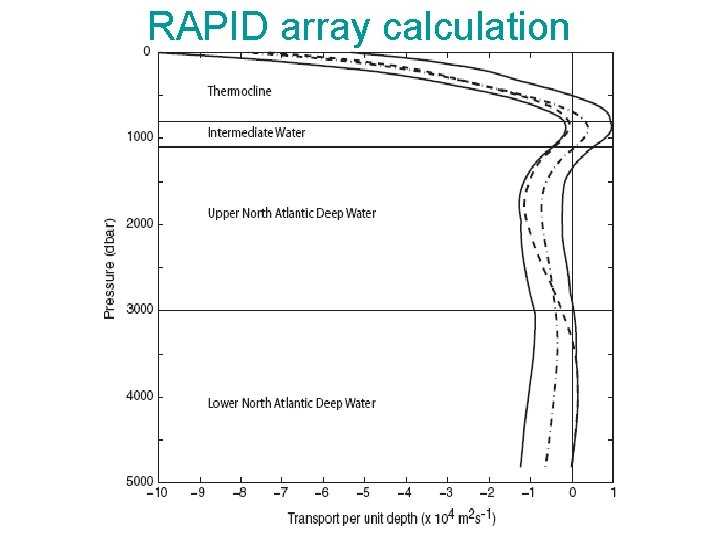
RAPID array calculation

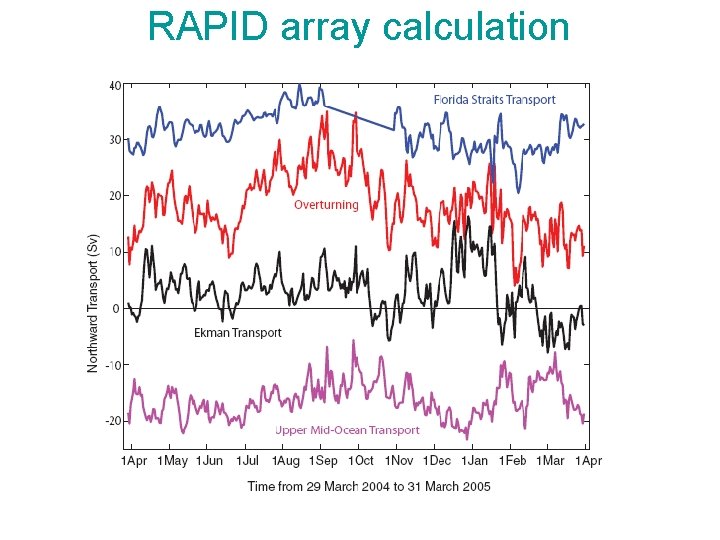
RAPID array calculation

Blackboard calculations…

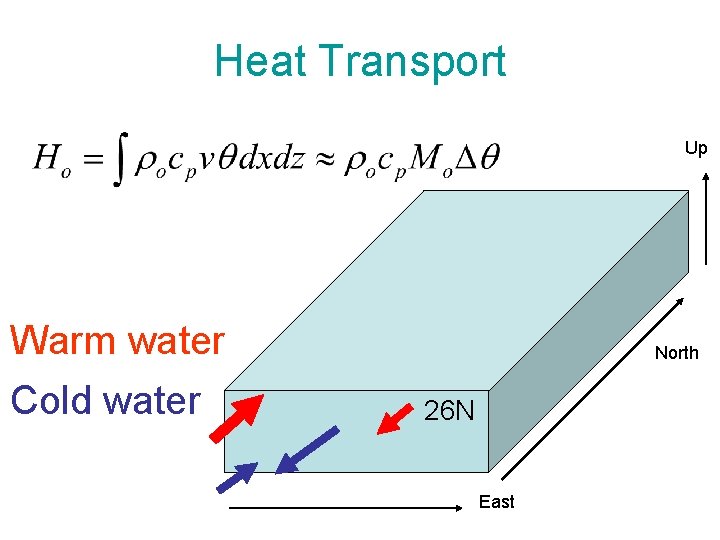
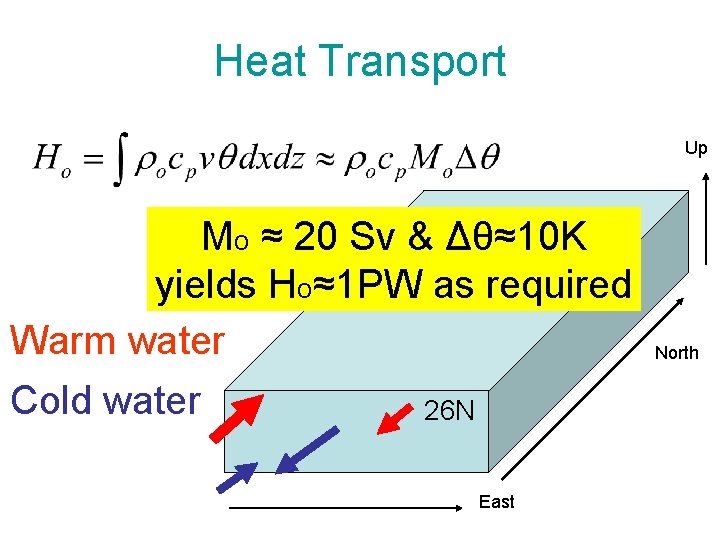
Heat Transport Up Warm water Cold water North 26 N East

Heat Transport Up Mo ≈ 20 Sv & Δθ≈10 K yields Ho≈1 PW as required Warm water Cold water 26 N East North

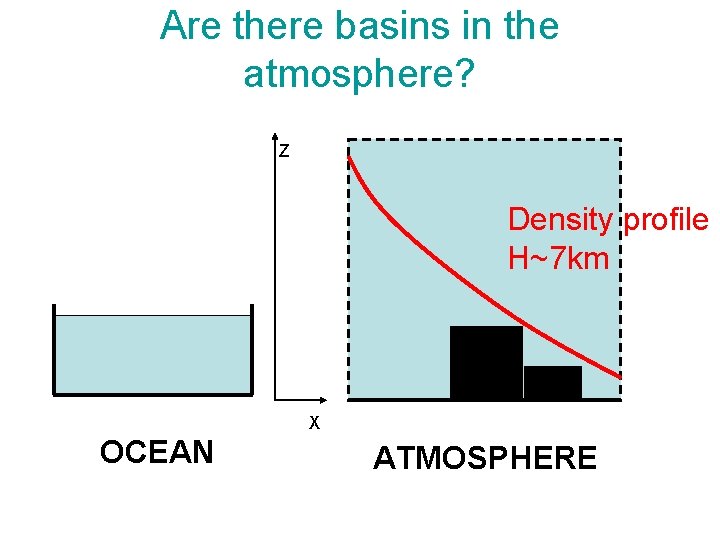
Are there basins in the atmosphere? Z Density profile H~7 km X OCEAN ATMOSPHERE

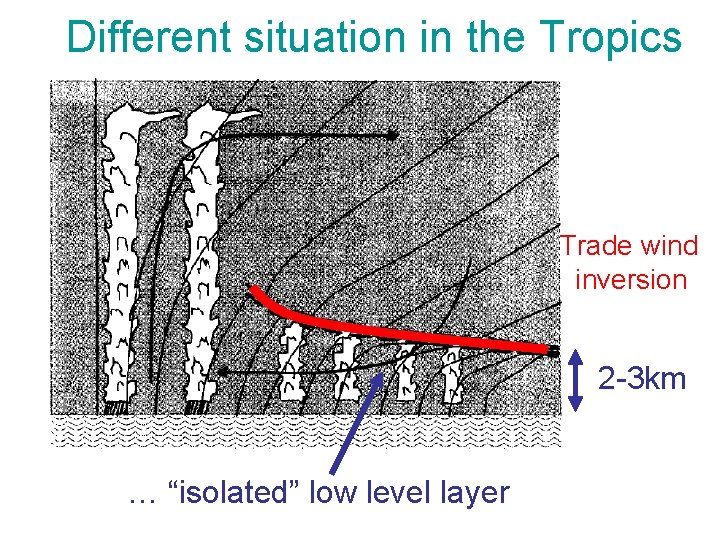
Different situation in the Tropics Trade wind inversion 2 -3 km … “isolated” low level layer

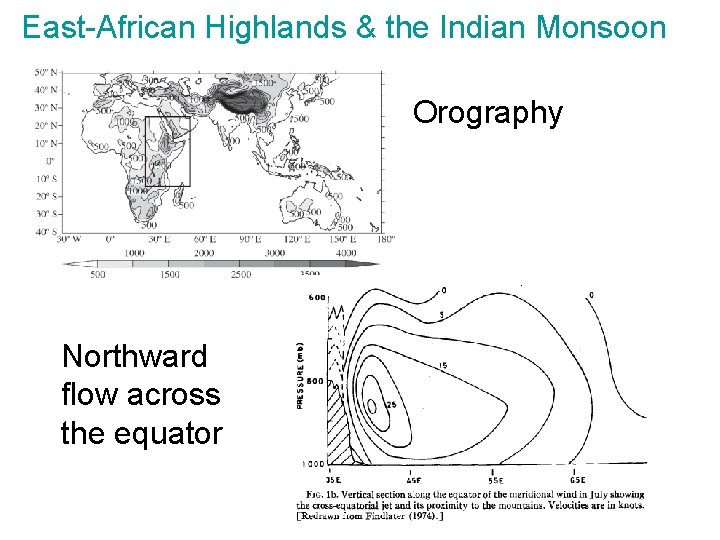
East-African Highlands & the Indian Monsoon Orography Northward flow across the equator

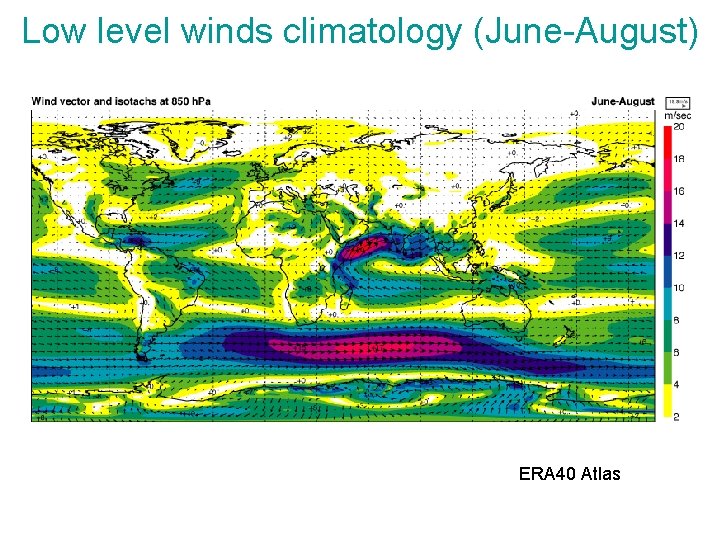
Low level winds climatology (June-August) ERA 40 Atlas

Channel: Atmosphere, Southern Ocean How to satisfy the energy constraint In a geometry in which <d. P/dx> = 0? • Hadley cell • Oceanic & atmospheric eddies

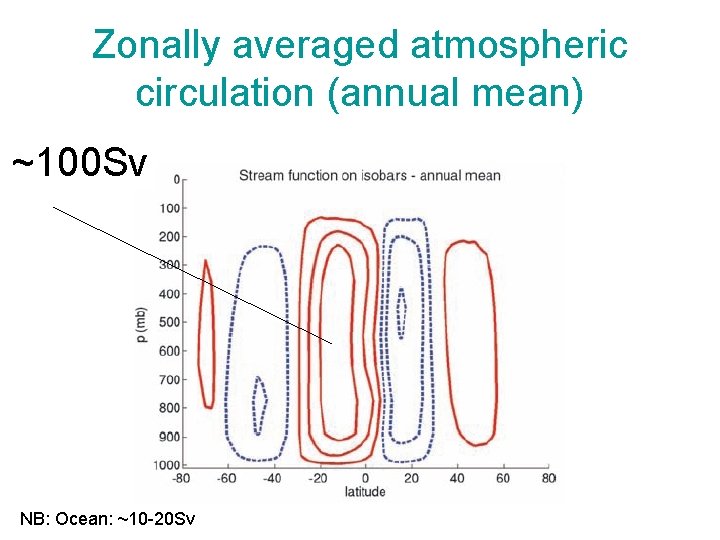
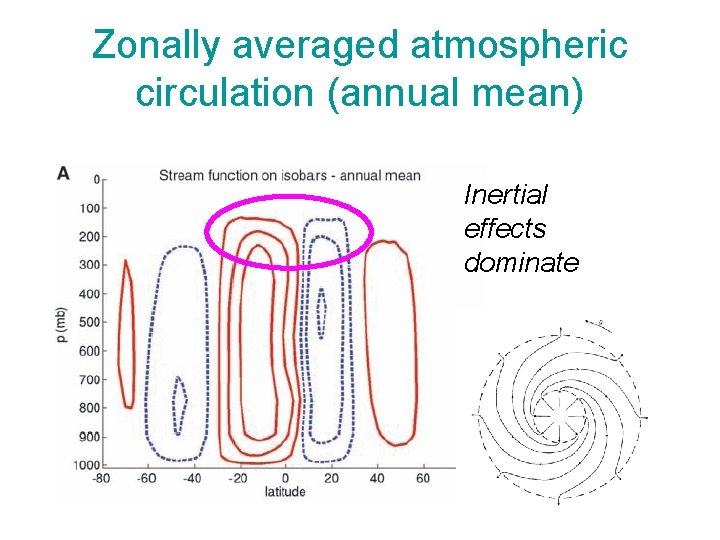
Zonally averaged atmospheric circulation (annual mean) ~100 Sv NB: Ocean: ~10 -20 Sv

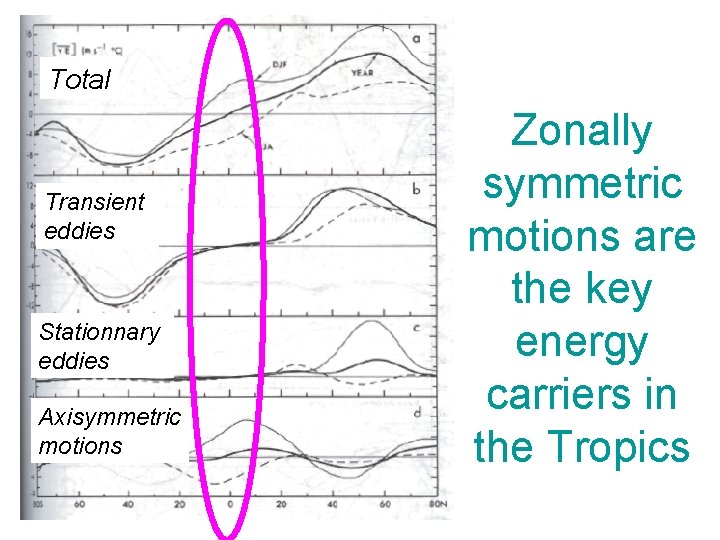
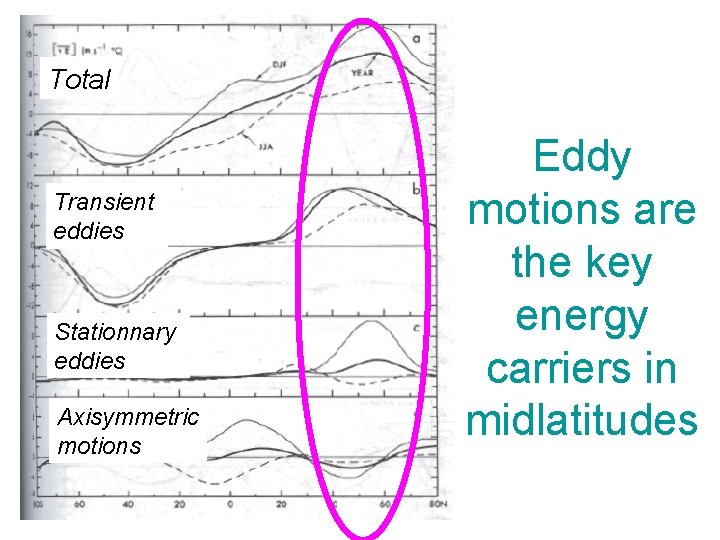
Total Transient eddies Stationnary eddies Axisymmetric motions Zonally symmetric motions are the key energy carriers in the Tropics

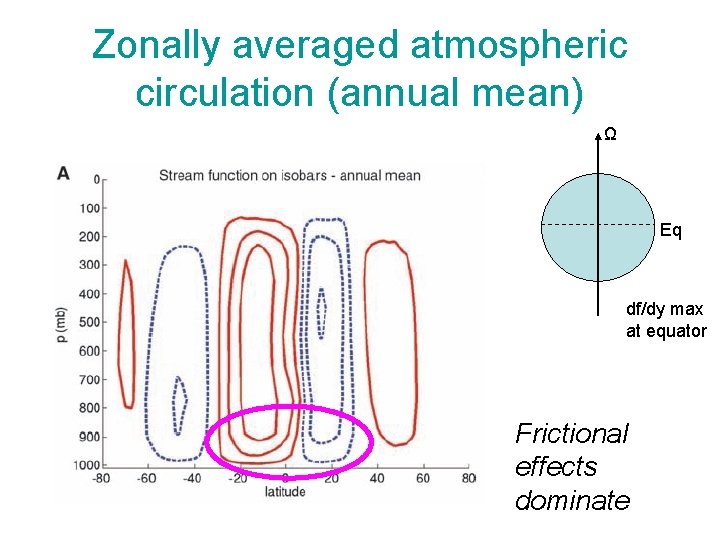
Zonally averaged atmospheric circulation (annual mean) Ω Eq df/dy max at equator Frictional effects dominate

Zonally averaged atmospheric circulation (annual mean) Inertial effects dominate

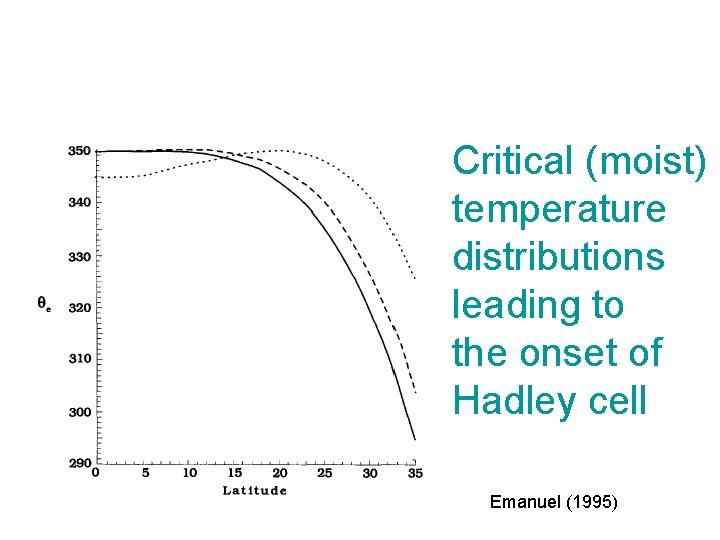
Critical (moist) temperature distributions leading to the onset of Hadley cell Emanuel (1995)

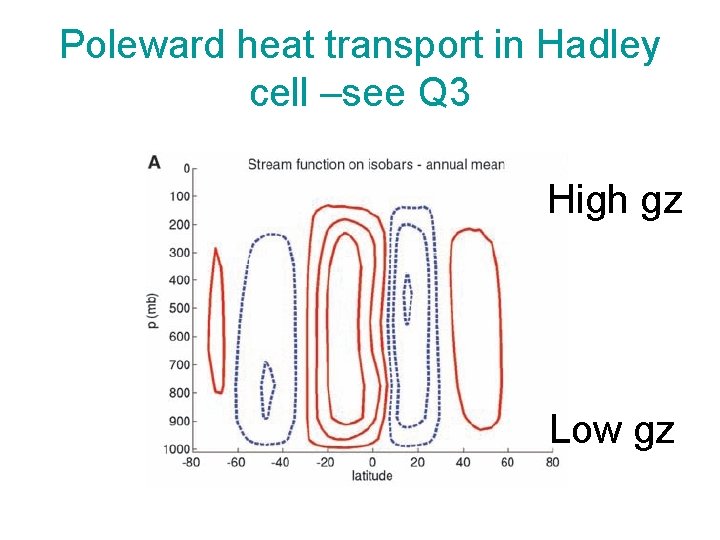
Poleward heat transport in Hadley cell –see Q 3 High gz Low gz

Eumetsat/Met. Office infrared picture (daily composite)

Total Transient eddies Stationnary eddies Axisymmetric motions Eddy motions are the key energy carriers in midlatitudes

Ocean eddies: the Movie

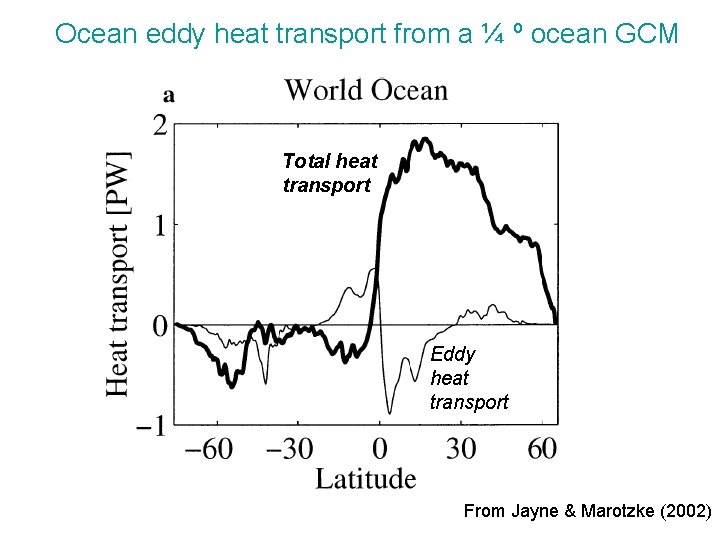
Ocean eddy heat transport from a ¼ º ocean GCM Total heat transport Eddy heat transport From Jayne & Marotzke (2002)

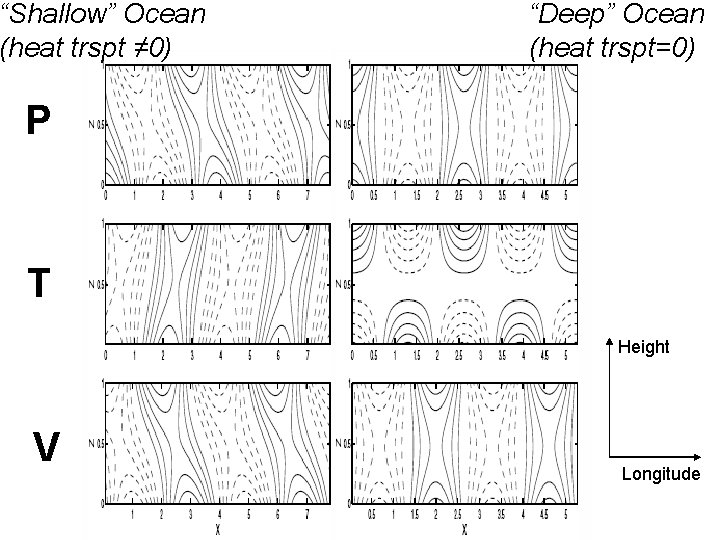
“Shallow” Ocean (heat trspt ≠ 0) “Deep” Ocean (heat trspt=0) P T Height V Longitude