ROTASI KINEMATIKA ROTASI Bila terjadi perubahan sudut dalam

ROTASI § KINEMATIKA ROTASI • Bila terjadi perubahan sudut dalam selang waktu tertentu, didefinisikan kecepatan sudut rata-rata sebagai : • Bila terjadi perubahan kecepatan sudut dalam selang waktu tertentu, didefinisikan percepatan sudut rata-rata sebagai : = Sudut [radian] = Kecepatan sudut [radian/s] = Percepatan sudut [radian/s 2 ] t = Waktu [s]

• Kecepatan dan percepatan sudut sesaat : • Persamaan-persamaan kinematika rotasi :

• Hubungan antara kecepatan linier dan kecepatan sudut • Hubungan antara percepatan linier dan percepatan sudut

Contoh Soal • Sebuah roda yang diameternya 3 m mempunyai kecepatan angular yang berkurang secara uniform dari 100 rpm pada t = 0 hingga behenti pada t = 4 sekon. Hitung percepatan tangensial dan percepatan normal sebuah titik di tepi roda pada t = 2 sekon.

Contoh Soal • Bulan berputar mengelilingi bumi dan kembali ke tempatnya semula setiap 28 hari. Bila jarak antara bumi dan bulan adalah 38, 4 x 104 km, hitunglah: a. Kecepatan linier b. Kecepatan angular c. Percepatan sentripetal bulan

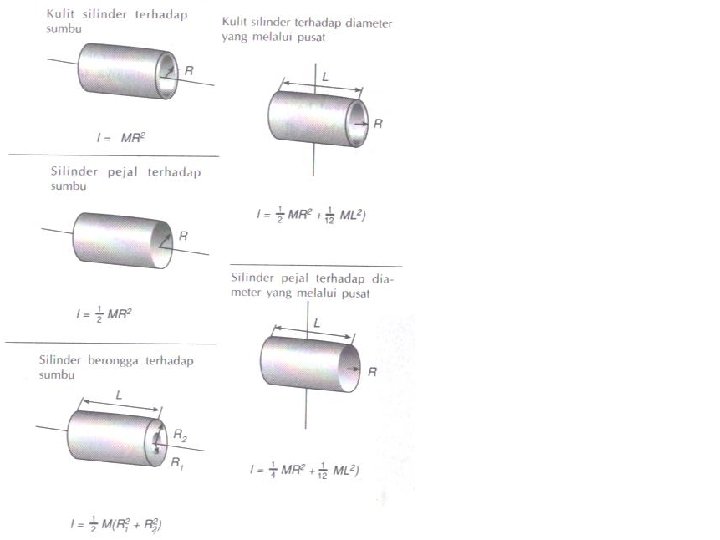
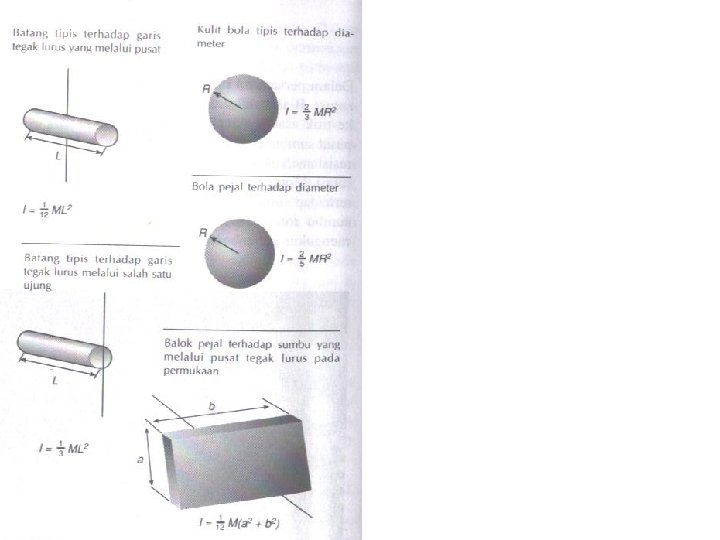
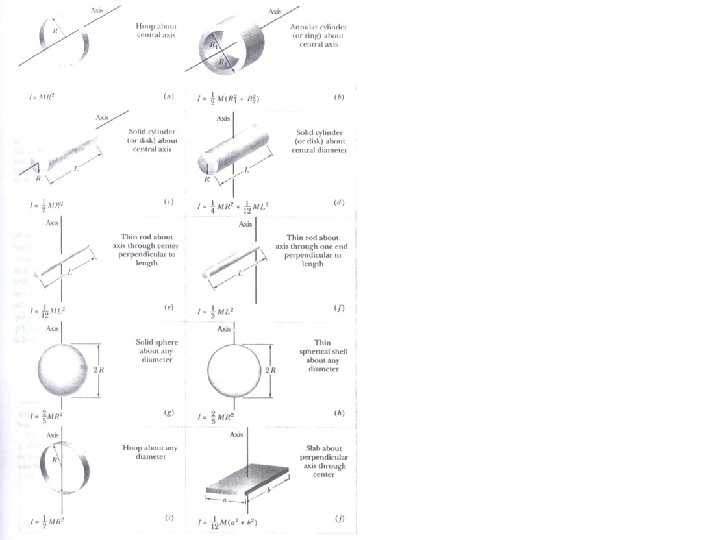
• Momen Inersia (rotasi) massa (translasi) Untuk sistem partikel energi kinetiknya : I disebut momen inersia dari sistem partikel Untuk benda tegar momen inersianya dapat dihitung dari :

Contoh Soal 5. 3 Suatu sistem terdiri dari dua buah benda bermassa sama m yang dihubungkan dengan sebuah batang kaku sepanjang L dengan massa yang dapat diabaikan. a). Bila sistem tersebut berputar dengan sumbu ditengah batang tentukan momen inersianya b). Tentukan momen inersianya bila berputar dengan sumbu pada ujung batang Jawab :

§ DINAMIKA ROTASI Sebuah benda berputar pada suatu sumbu disebabkan karena adanya momen gaya atau torka/torsi (torque) Hukum Newton II untuk rotasi : § KERJA DAN DAYA ROTASI

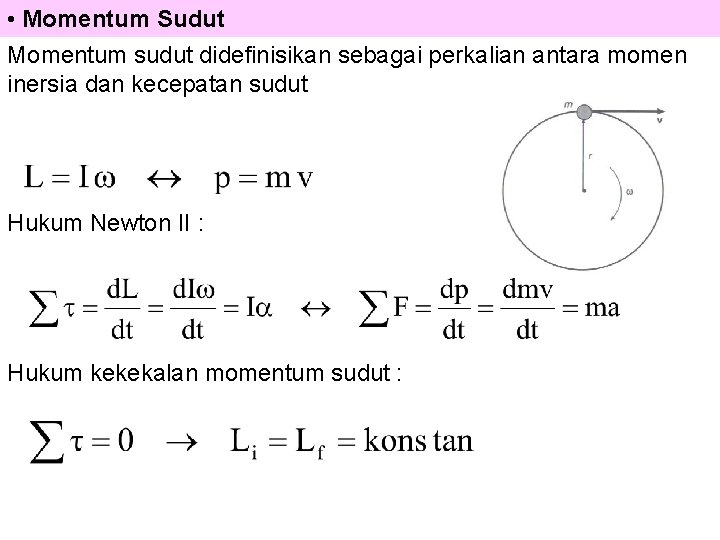
• Momentum Sudut Momentum sudut didefinisikan sebagai perkalian antara momen inersia dan kecepatan sudut Hukum Newton II : Hukum kekekalan momentum sudut :

• Gerak Menggelinding Sebuah bola menggelinding di atas bidang datar tanpa slip Titik kontak antara bola dan bidang datar bergerak sejauh s Pusat massa terletak di atas titik kontak juga bergerak sejauh s Kondisi menggelinding :

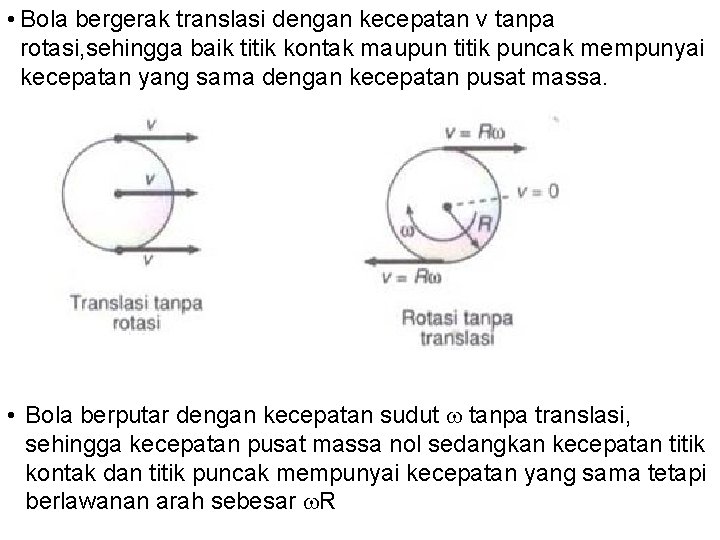
• Bola bergerak translasi dengan kecepatan v tanpa rotasi, sehingga baik titik kontak maupun titik puncak mempunyai kecepatan yang sama dengan kecepatan pusat massa. • Bola berputar dengan kecepatan sudut tanpa translasi, sehingga kecepatan pusat massa nol sedangkan kecepatan titik kontak dan titik puncak mempunyai kecepatan yang sama tetapi berlawanan arah sebesar R

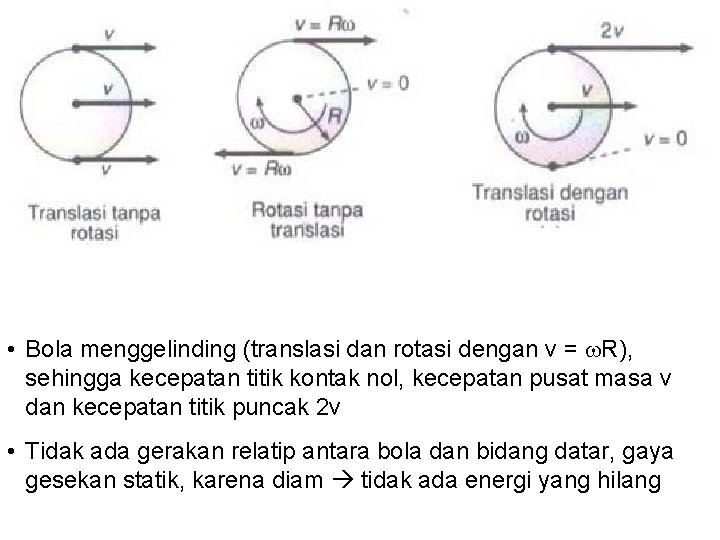
• Bola menggelinding (translasi dan rotasi dengan v = R), sehingga kecepatan titik kontak nol, kecepatan pusat masa v dan kecepatan titik puncak 2 v • Tidak ada gerakan relatip antara bola dan bidang datar, gaya gesekan statik, karena diam tidak ada energi yang hilang

Contoh Soal • Sebuah silinder pejal bermassa M dan Jari-jari R diletakkan pada bidang miring dengan kemiringan Ɵ terhadap bidang horisontal yang mempunyai kekasaran tertentu. Setelah dilepas silinder tersebut menggelinding, tentukan kecepatan silinder setelah sampai di kaki bidang miring!