ROTAMERS OF ISOPRENE INFRARED SPECTROSCOPY IN HELIUM DROPLETS

ROTAMERS OF ISOPRENE: INFRARED SPECTROSCOPY IN HELIUM DROPLETS AND AB INITIO THERMOCHEMISTRY Peter R. Franke and Gary E. Douberly Department of Chemistry, University of Georgia, Athens, Georgia 30602 -2556, USA RG 03

Atmospheric Significance of Isoprene • Isoprene (C 5 H 8) is emitted by trees and shrubs. • One of the most substantial natural sources of volatile organic carbon • Second only to methane • Atmospheric lifetime is ~ 2 hours. • Fate is primarily OH addition to its double bonds. Guentheret et al. J. Geophys. Res-Atmos. 1995, 100, 8873.

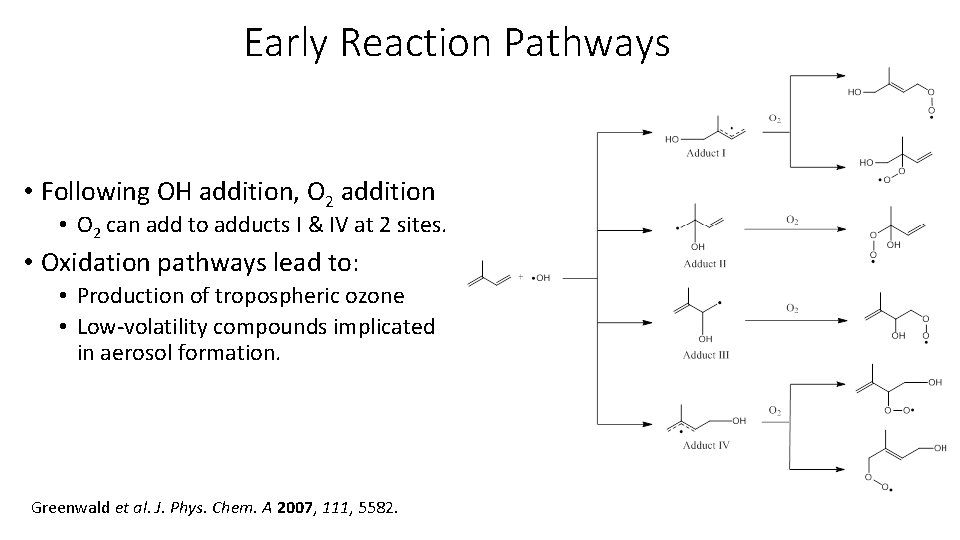
Early Reaction Pathways • Following OH addition, O 2 addition • O 2 can add to adducts I & IV at 2 sites. • Oxidation pathways lead to: • Production of tropospheric ozone • Low-volatility compounds implicated in aerosol formation. Greenwald et al. J. Phys. Chem. A 2007, 111, 5582.

Overview of Talk I. Thermochemistry Summarize ab initio thermochemistry results II. Infrared Spectroscopy Present a new vibrational spectrum of isoprene between 2860 -3120 cm-1 III. Anharmonic Simulations Demonstration of simulating the anharmonic resonances • • Introductory level Resonance diagnostics & treatment Corrections for higher-order effects Applicability/limitations

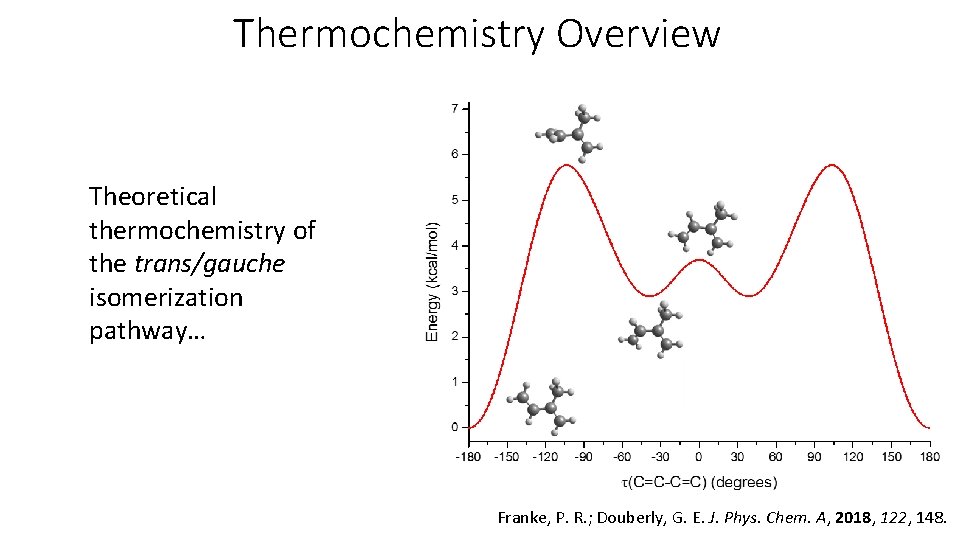
Thermochemistry Overview Theoretical thermochemistry of the trans/gauche isomerization pathway… Franke, P. R. ; Douberly, G. E. J. Phys. Chem. A, 2018, 122, 148.

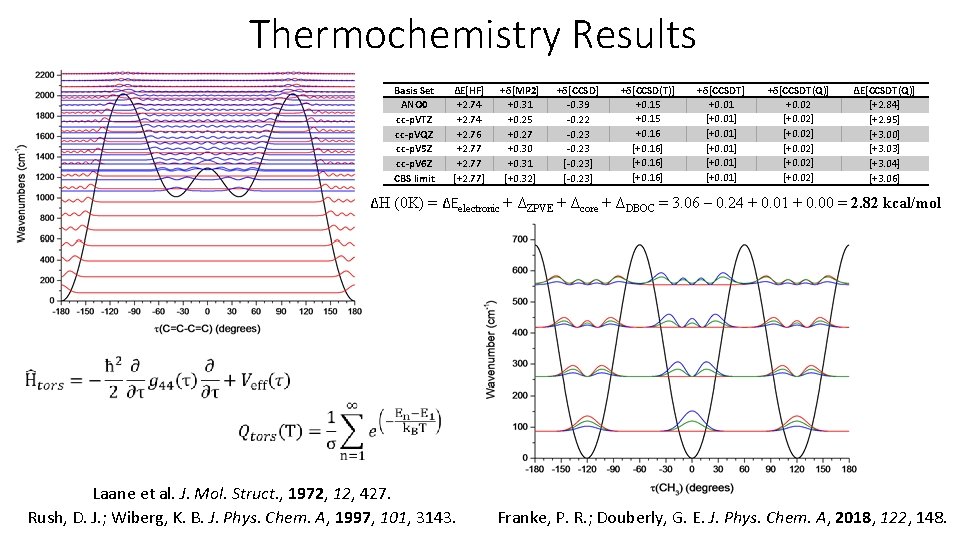
Thermochemistry Results Basis Set ANO 0 cc-p. VTZ cc-p. VQZ cc-p. V 5 Z cc-p. V 6 Z CBS limit ΔE[HF] +2. 74 +2. 76 +2. 77 [+2. 77] +δ[MP 2] +0. 31 +0. 25 +0. 27 +0. 30 +0. 31 [+0. 32] +δ[CCSD] -0. 39 -0. 22 -0. 23 [-0. 23] +δ[CCSD(T)] +0. 15 +0. 16 [+0. 16] +δ[CCSDT] +0. 01 [+0. 01] +δ[CCSDT(Q)] +0. 02 [+0. 02] ΔE[CCSDT(Q)] [+2. 84] [+2. 95] [+3. 00] [+3. 03] [+3. 04] [+3. 06] ΔH (0 K) = ΔEelectronic + ΔZPVE + Δcore + ΔDBOC = 3. 06 – 0. 24 + 0. 01 + 0. 00 = 2. 82 kcal/mol Laane et al. J. Mol. Struct. , 1972, 12, 427. Rush, D. J. ; Wiberg, K. B. J. Phys. Chem. A, 1997, 101, 3143. Franke, P. R. ; Douberly, G. E. J. Phys. Chem. A, 2018, 122, 148.

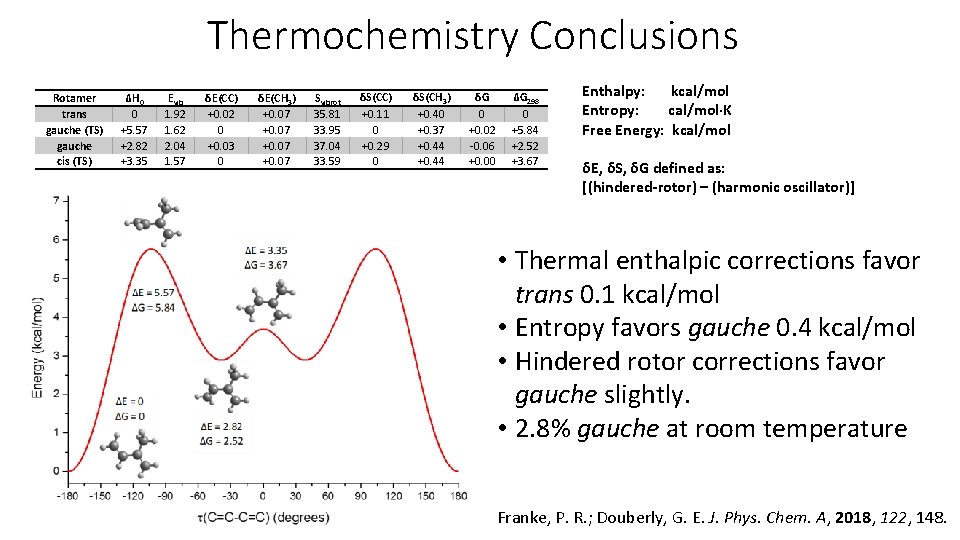
Thermochemistry Conclusions Rotamer trans gauche (TS) gauche cis (TS) ΔH 0 0 +5. 57 +2. 82 +3. 35 Evib 1. 92 1. 62 2. 04 1. 57 δE(CC) +0. 02 0 +0. 03 0 δE(CH 3) +0. 07 Svibrot 35. 81 33. 95 37. 04 33. 59 δS(CC) +0. 11 0 +0. 29 0 δS(CH 3) +0. 40 +0. 37 +0. 44 δG 0 +0. 02 -0. 06 +0. 00 ΔG 298 0 +5. 84 +2. 52 +3. 67 Enthalpy: kcal/mol Entropy: cal/mol·K Free Energy: kcal/mol δE, δS, δG defined as: [(hindered-rotor) – (harmonic oscillator)] • Thermal enthalpic corrections favor trans 0. 1 kcal/mol • Entropy favors gauche 0. 4 kcal/mol • Hindered rotor corrections favor gauche slightly. • 2. 8% gauche at room temperature Franke, P. R. ; Douberly, G. E. J. Phys. Chem. A, 2018, 122, 148.

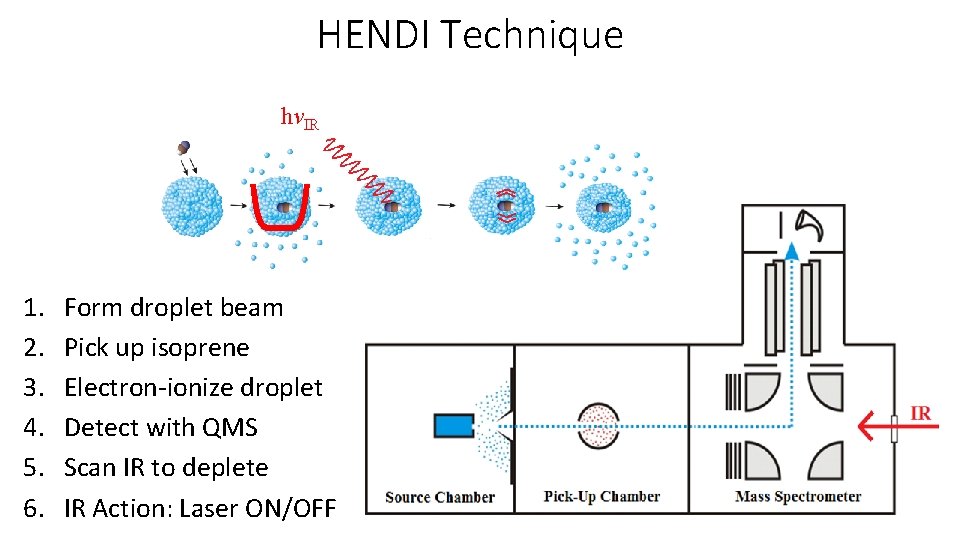
HENDI Technique hνIR 1. 2. 3. 4. 5. 6. Form droplet beam Pick up isoprene Electron-ionize droplet Detect with QMS Scan IR to deplete IR Action: Laser ON/OFF

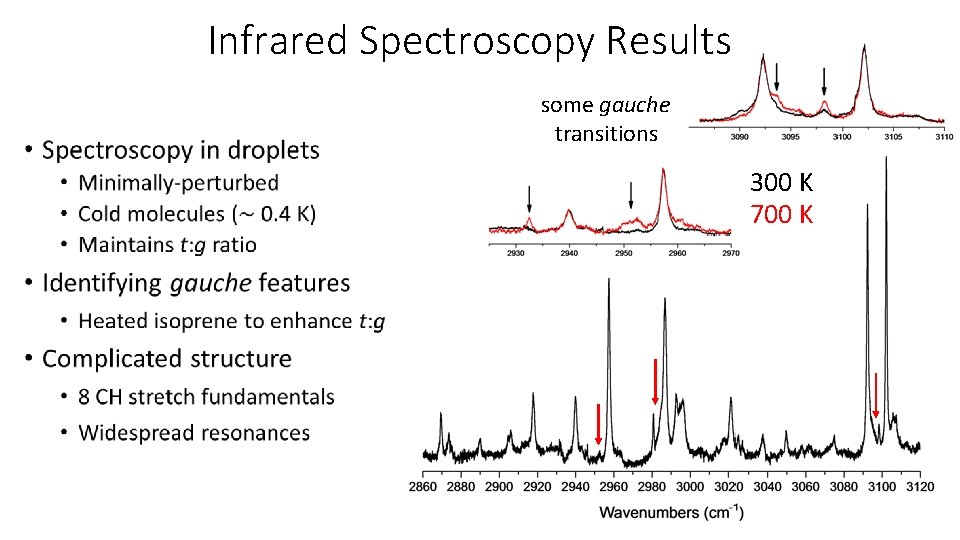
Infrared Spectroscopy Results some gauche transitions 300 K 700 K

Anharmonic Theory: VPT 2 •

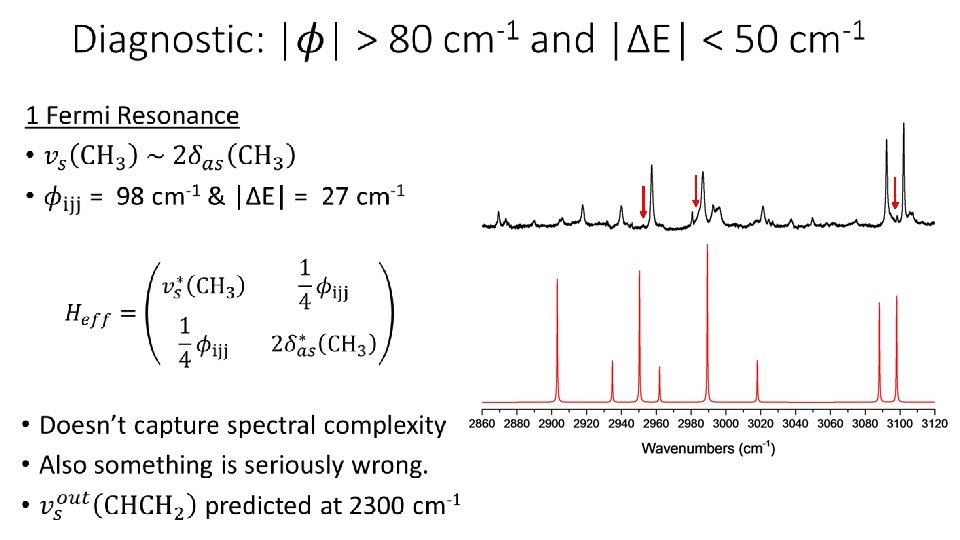
Challenges Associated with CH Stretches Primary: Fermi Resonance • Harmonic frequency of a CH stretching vibration is nearly double the harmonic frequencies of many of the CH bending modes (also C=C stretch). • Harmonic approximation is unacceptable. • Full VPT 2 can be even worse (due to near zero denominators). • Well established that matrix diagonalization, following partial VPT 2, can correct this. Secondary: Series of Connected Fermi Resonances • CH bending vibrations can have resonances of their own. • Now must consider series of resonances connected to each other • Resonance treatment can become quite complicated.

Anharmonic Theory: VPT 2+K • Defined method of correcting VPT 2 for resonances • VPT 2+K simulations can successfully model CH stretching spectra • Procedure: • • Identify strong (i. e. resonant) interactions Treat weak interactions with VPT 2. Build an effective Hamiltonian matrix of strongly-interacting states. Diagonalize to obtain anharmonic transitions & mixing • Include Darling-Dennison couplings to go even further beyond VPT 2. • See reference for implementation details, equations, etc. • Question: How do we decide which interactions are weak/strong? Rosnik, A. M. ; Polik, W. F. Mol. Phys. 2014, 112, 261.

Fermi Resonance Identification • “Potentially” Resonant Terms

Brief Digression: Theoretical Methods • Hybrid Force Field • • Cubic/quartic force constants at CCSD(T)/ANO 0. Quadratic force constants at CCSD(T)/ANO 1. If normal coordinates do not change drastically, this works well. Force field computed using CFOUR; VPT 2+K in Mathematica • Transition Intensities • Electrical harmonicity • Distribute harmonic intensity proportional to elements of squared eigenvectors. • e. g. dark state mixes 80: 20 with bright state so it has 20% of bright state’s intensity. • Overtones/combinations must be contained in effective Hamiltonian to have intensity.

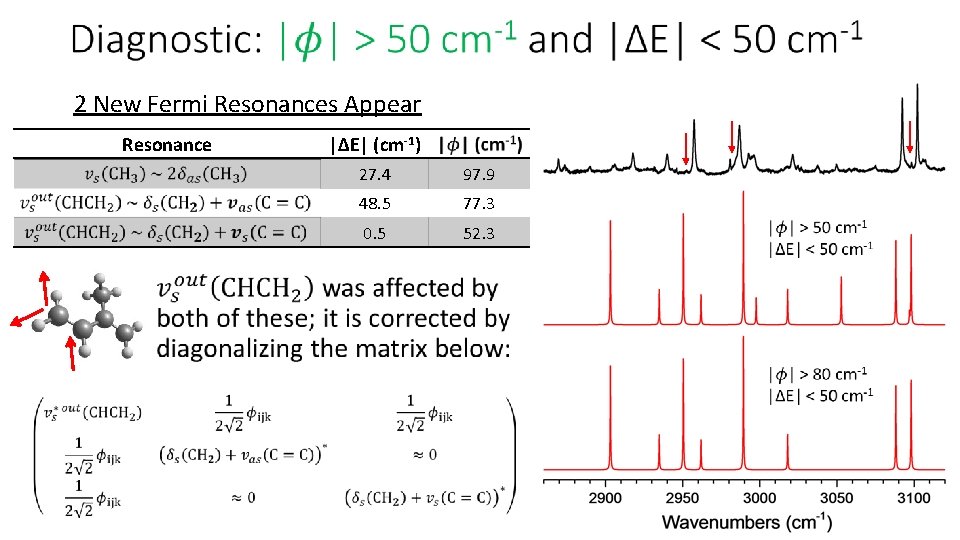
2 New Fermi Resonances Appear Resonance • |ΔE| (cm-1) 27. 4 97. 9 48. 5 77. 3 0. 5 52. 3

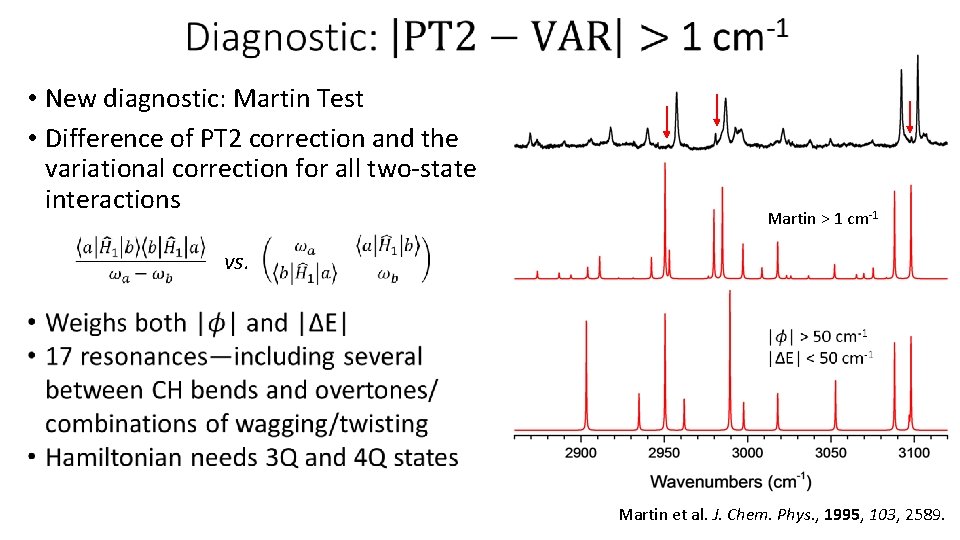
• New diagnostic: Martin Test • Difference of PT 2 correction and the variational correction for all two-state interactions Martin > 1 cm-1 vs. Martin et al. J. Chem. Phys. , 1995, 103, 2589.

Systematic Way to Handle Resonances •

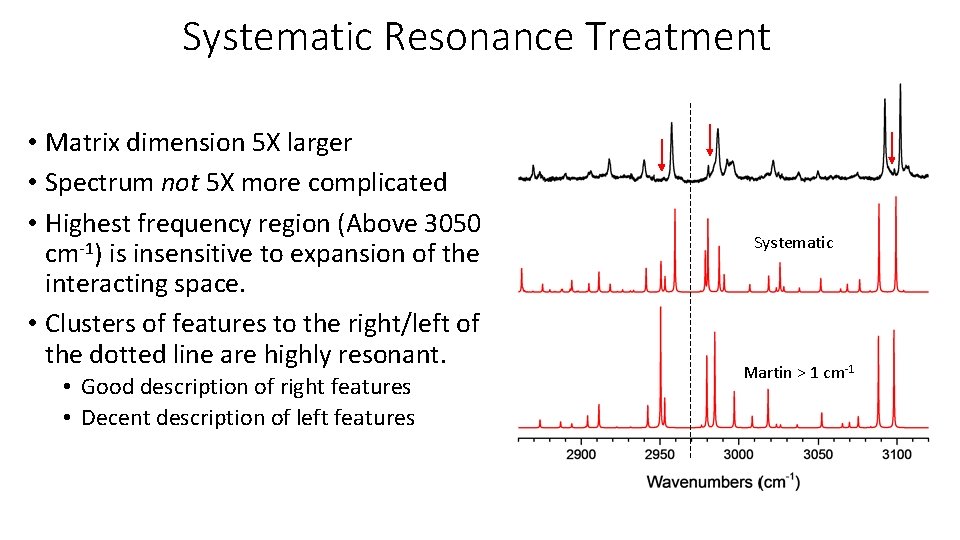
Systematic Resonance Treatment • Matrix dimension 5 X larger • Spectrum not 5 X more complicated • Highest frequency region (Above 3050 cm-1) is insensitive to expansion of the interacting space. • Clusters of features to the right/left of the dotted line are highly resonant. • Good description of right features • Decent description of left features Systematic Martin > 1 cm-1

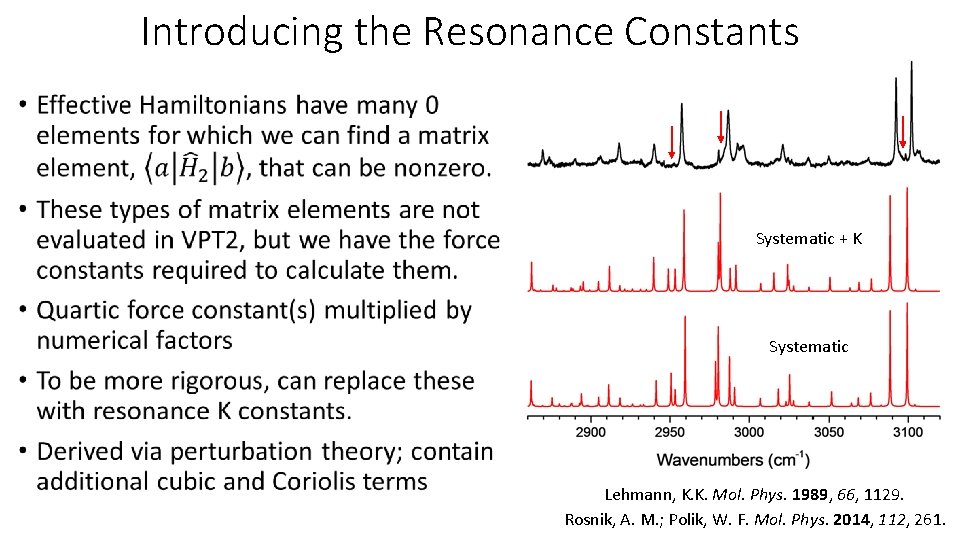
Introducing the Resonance Constants • Systematic + K Systematic Lehmann, K. K. Mol. Phys. 1989, 66, 1129. Rosnik, A. M. ; Polik, W. F. Mol. Phys. 2014, 112, 261.

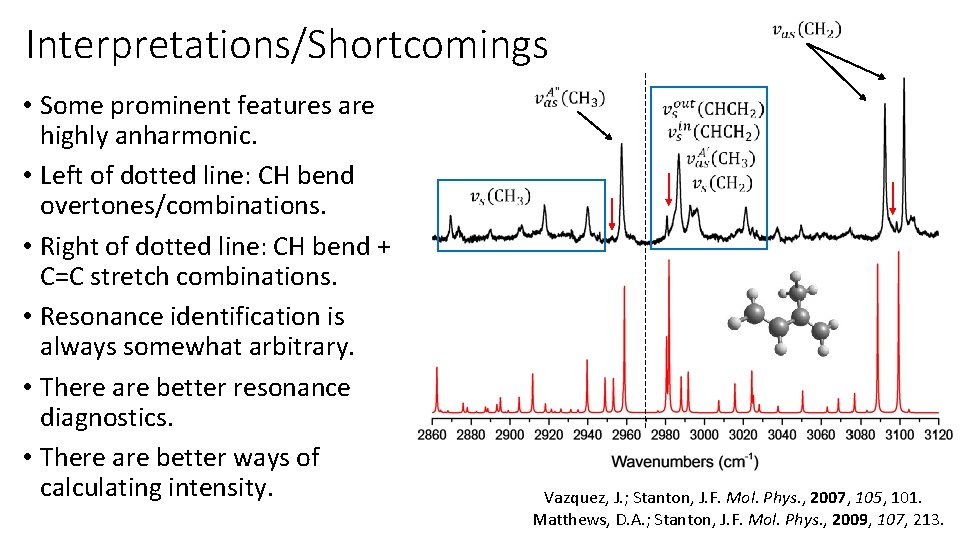
Interpretations/Shortcomings • Some prominent features are highly anharmonic. • Left of dotted line: CH bend overtones/combinations. • Right of dotted line: CH bend + C=C stretch combinations. • Resonance identification is always somewhat arbitrary. • There are better resonance diagnostics. • There are better ways of calculating intensity. Vazquez, J. ; Stanton, J. F. Mol. Phys. , 2007, 105, 101. Matthews, D. A. ; Stanton, J. F. Mol. Phys. , 2009, 107, 213.

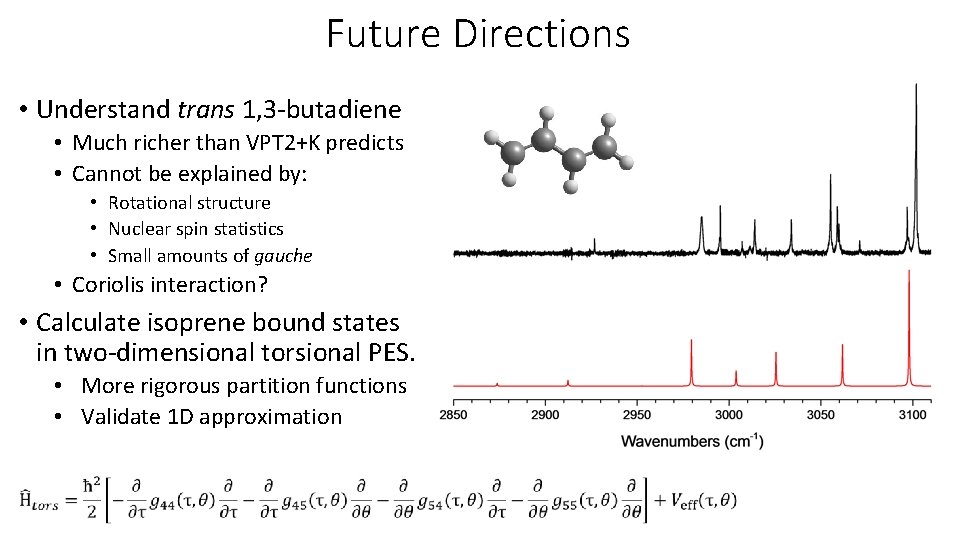
Future Directions • Understand trans 1, 3 -butadiene • Much richer than VPT 2+K predicts • Cannot be explained by: • Rotational structure • Nuclear spin statistics • Small amounts of gauche • Coriolis interaction? • Calculate isoprene bound states in two-dimensional torsional PES. • More rigorous partition functions • Validate 1 D approximation

We acknowledge support from the National Science Foundation. Thank you for your attention!