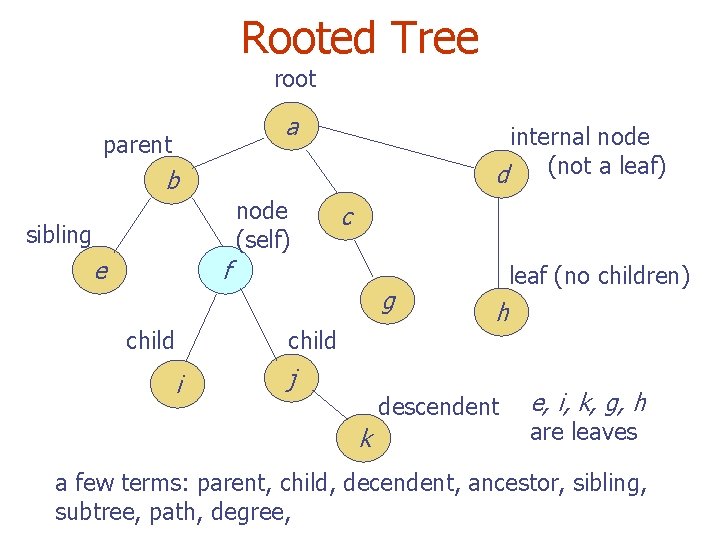
Rooted Tree root a parent internal node not

Rooted Tree root a parent internal node (not a leaf) d b node (self) sibling e c f child i g child j leaf (no children) h descendent k e, i, k, g, h are leaves a few terms: parent, child, decendent, ancestor, sibling, subtree, path, degree,

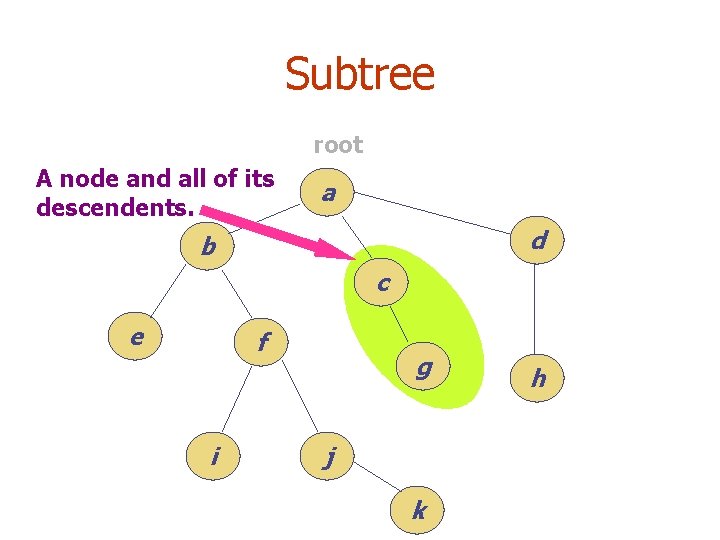
Subtree root A node and all of its descendents. a d b c e f i g j k h

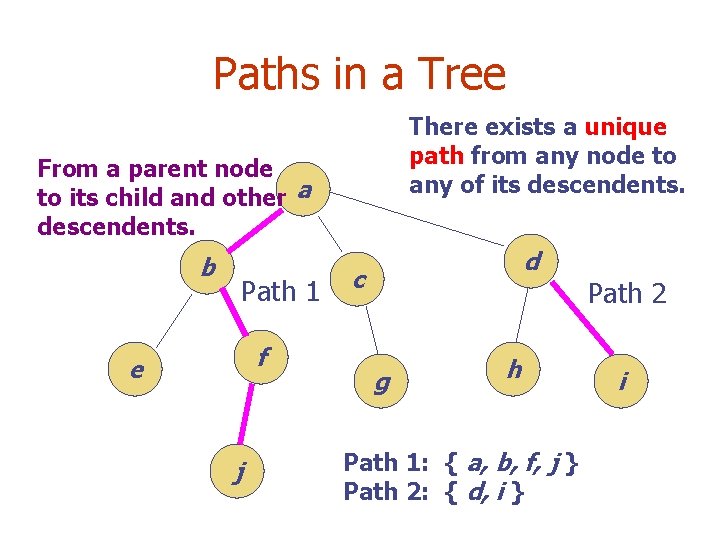
Paths in a Tree There exists a unique path from any node to any of its descendents. From a parent node to its child and other a descendents. b Path 1 f e j d c g h Path 1: { a, b, f, j } Path 2: { d, i } Path 2 i

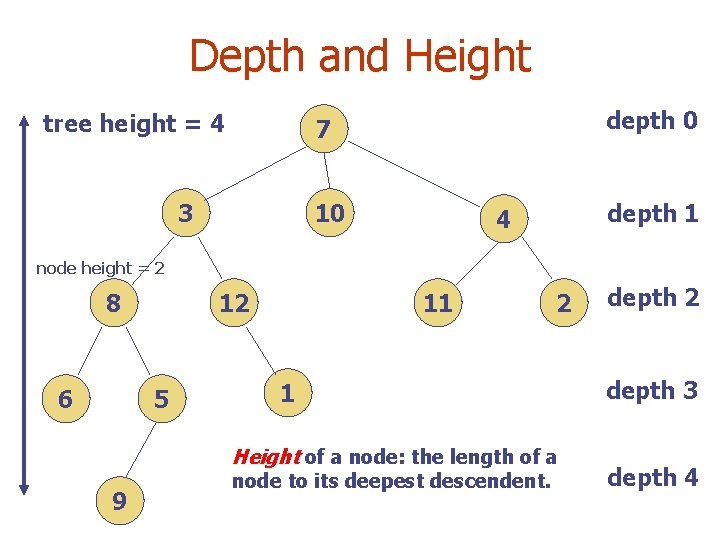
Depth and Height tree height = 4 depth 0 7 3 10 depth 1 4 node height = 2 8 6 12 5 11 2 1 Height of a node: the length of a 9 node to its deepest descendent. depth 2 depth 3 depth 4

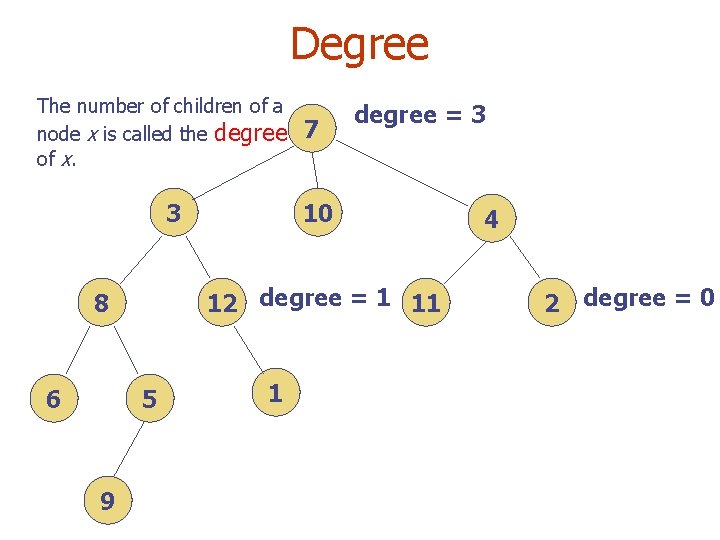
Degree The number of children of a node x is called the degree of x. 3 5 9 10 12 degree = 1 11 8 6 7 degree = 3 1 4 2 degree = 0

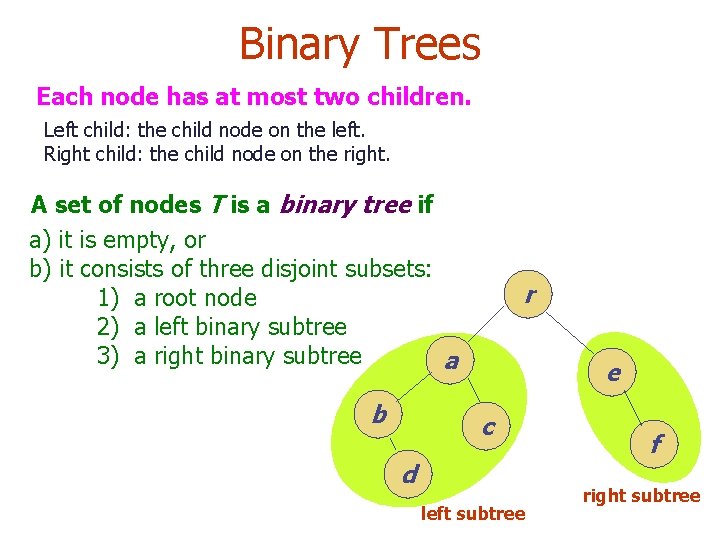
Binary Trees Each node has at most two children. Left child: the child node on the left. Right child: the child node on the right. A set of nodes T is a binary tree if a) it is empty, or b) it consists of three disjoint subsets: 1) a root node 2) a left binary subtree 3) a right binary subtree a b r e c d left subtree f right subtree

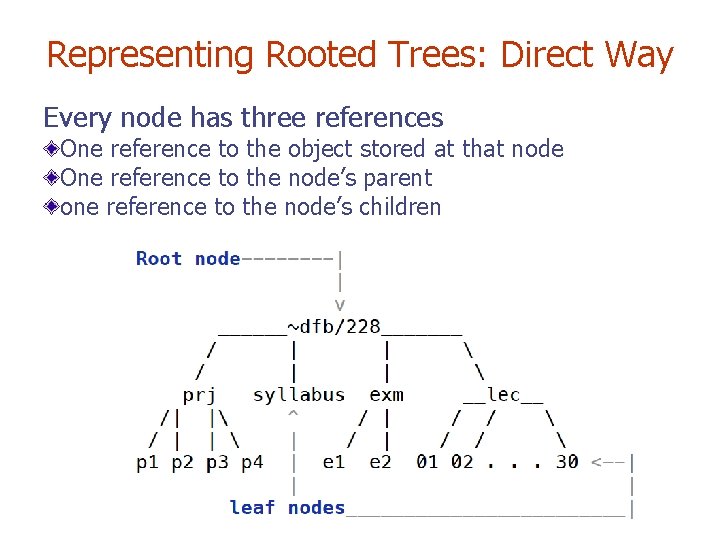
Representing Rooted Trees: Direct Way Every node has three references One reference to the object stored at that node One reference to the node’s parent one reference to the node’s children

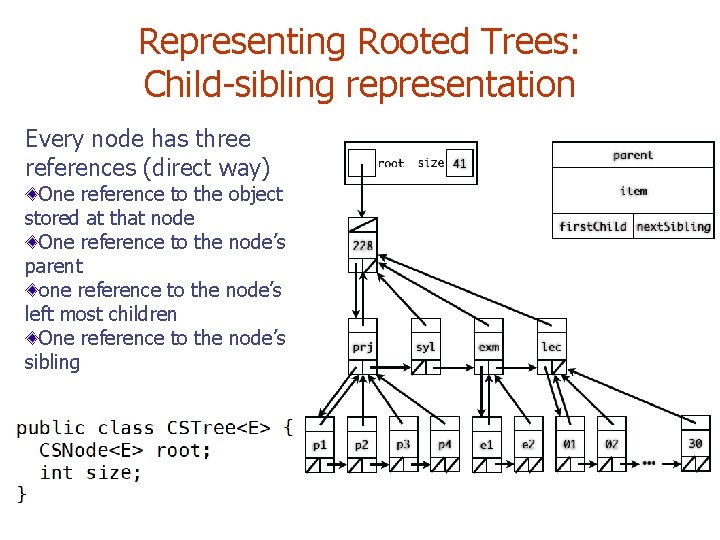
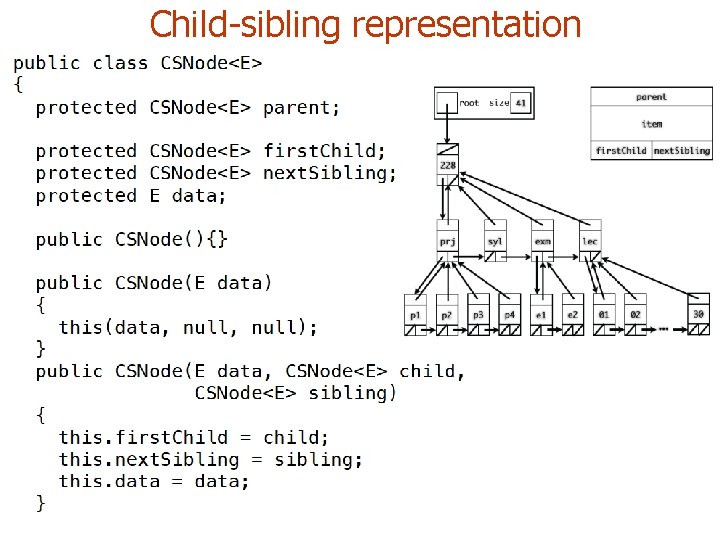
Representing Rooted Trees: Child-sibling representation Every node has three references (direct way) One reference to the object stored at that node One reference to the node’s parent one reference to the node’s left most children One reference to the node’s sibling

Child-sibling representation

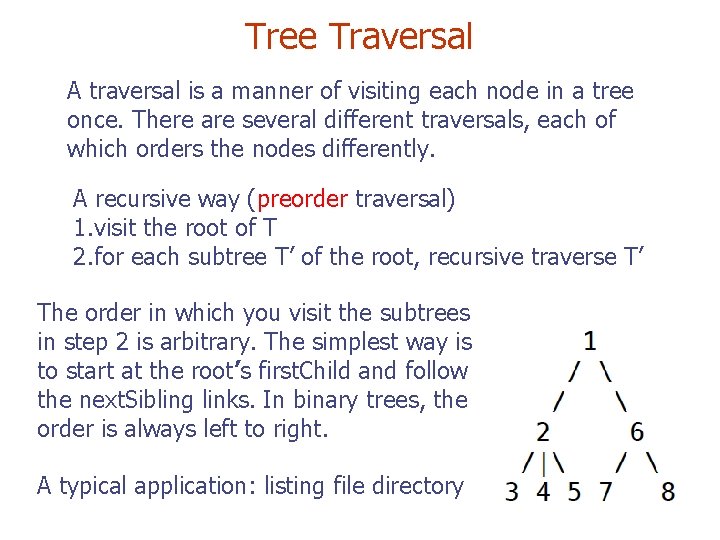
Tree Traversal A traversal is a manner of visiting each node in a tree once. There are several different traversals, each of which orders the nodes differently. A recursive way (preorder traversal) 1. visit the root of T 2. for each subtree T’ of the root, recursive traverse T’ The order in which you visit the subtrees in step 2 is arbitrary. The simplest way is to start at the rootʼs first. Child and follow the next. Sibling links. In binary trees, the order is always left to right. A typical application: listing file directory

Implementation What is the time complexity?

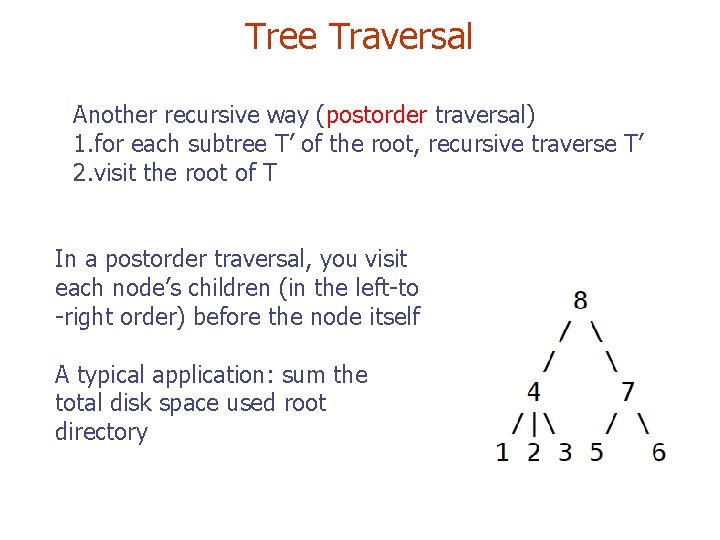
Tree Traversal Another recursive way (postorder traversal) 1. for each subtree T’ of the root, recursive traverse T’ 2. visit the root of T In a postorder traversal, you visit each node’s children (in the left-to -right order) before the node itself A typical application: sum the total disk space used root directory

Postorder tree Traversal

Tree Traversal Another recursive way (inorder traversal for a binary tree) 1. recursively traverse T’s left subtree 2. visit the root of T 3. recursively traverse T’s right subtree Yet another way (level order traversal) 1. visit the root of T 2. visit all depth-1 nodes from left to right 3. visit all depth-2 nodes, and so on how would you implement this?

Implementing Level Traversal Enqueue the root 1. Dequeue a node 2. Visit it 3. Enqueue its children (in order from left to right)

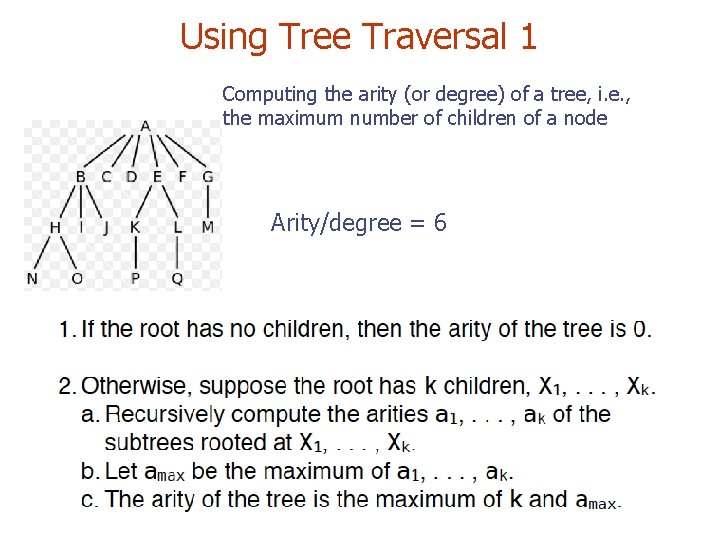
Using Tree Traversal 1 Computing the arity (or degree) of a tree, i. e. , the maximum number of children of a node Arity/degree = 6

Computing arity

Using Tree Traversal 2 Computing the height of a tree Using recursive 1. If the root has no children, the height is 0 2. Otherwise, the height is 1+max(height(leftsubtree), height(rightsubtree)

Computing tree height

Expression Trees An expression tree is a binary tree that represents an arithmetic expression • leaves are operands • internal nodes are operators prefix infix postfix

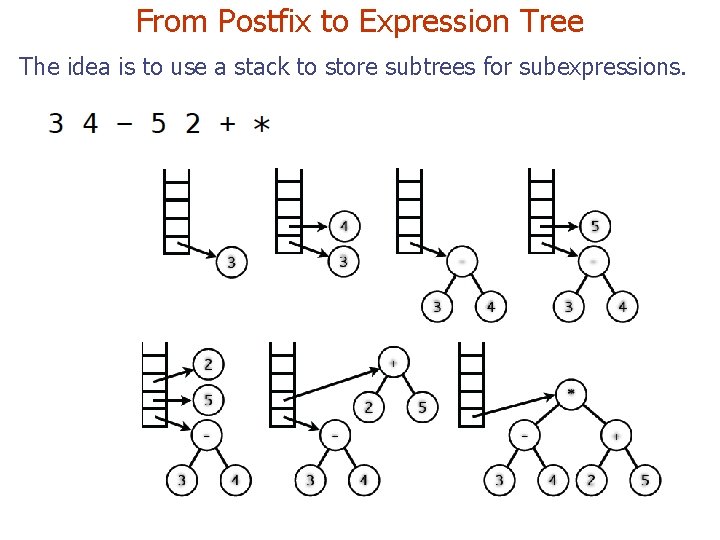
From Postfix to Expression Tree The idea is to use a stack to store subtrees for subexpressions.

Evaluating an expression tree

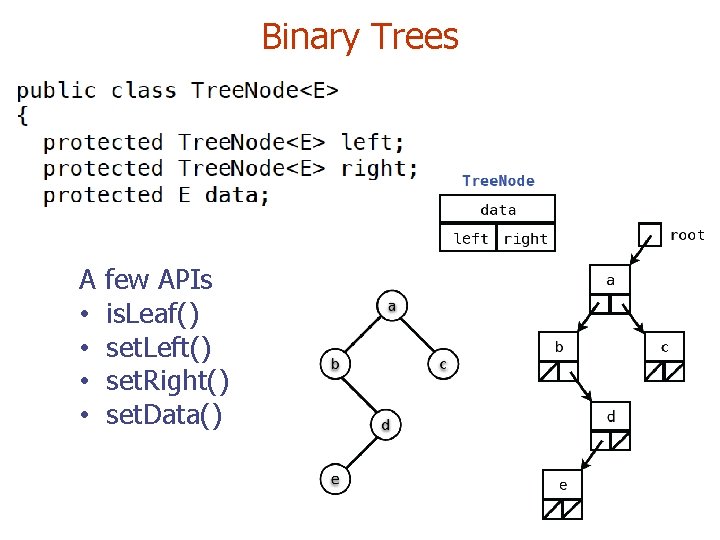
Binary Trees A • • few APIs is. Leaf() set. Left() set. Right() set. Data()

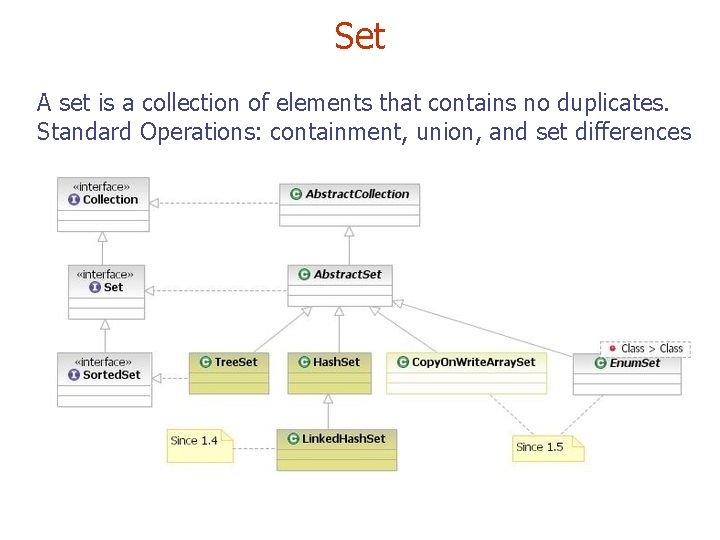
Set A set is a collection of elements that contains no duplicates. Standard Operations: containment, union, and set differences

Binary Search Tree A binary search tree is often used to implement a set where the element type if comparable. Property: For any node X, every key (element) in the left subtree of X is less than X’s key, and every key in the right subtree of X is greater than X’s key A same set of elements may have different BSTs, and an inorder traversal of a binary search tree visits the nodes in sorted order.

Building a BST for a set

Contains(c) Checking if a given element is C contained by a set is easier when the set is represented by a BST

Contains(c)

Add(k) The worst-case time needed to search for a key or to add a key to a BST T is O(height(T)).

Building a BST for a set Starting from a root, adding elements in the set one by one The tree built for a set of elements depends on the insertion order. The tree can be in two extreme cases: 1. Well-balanced tree (best case) 2. Very unbalanced tree (worst case)

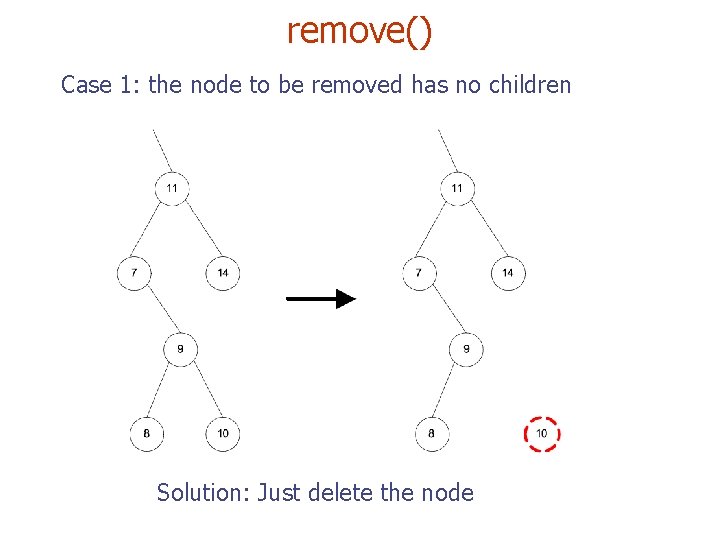
remove() Case 1: the node to be removed has no children Solution: Just delete the node

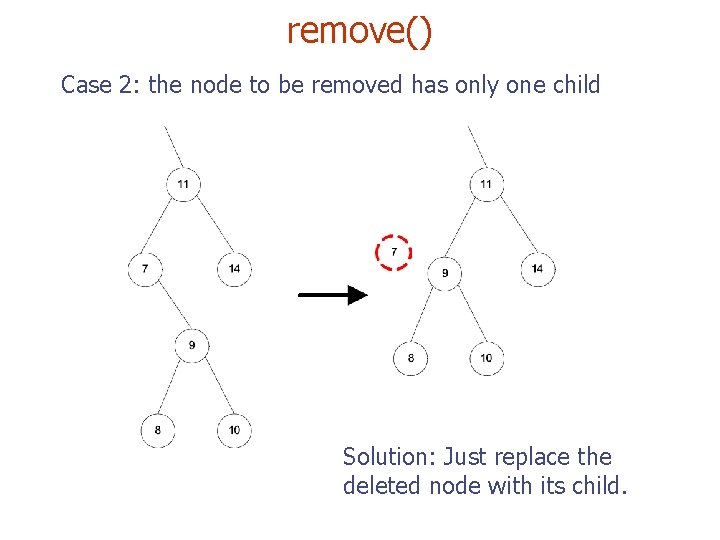
remove() Case 2: the node to be removed has only one child Solution: Just replace the deleted node with its child.

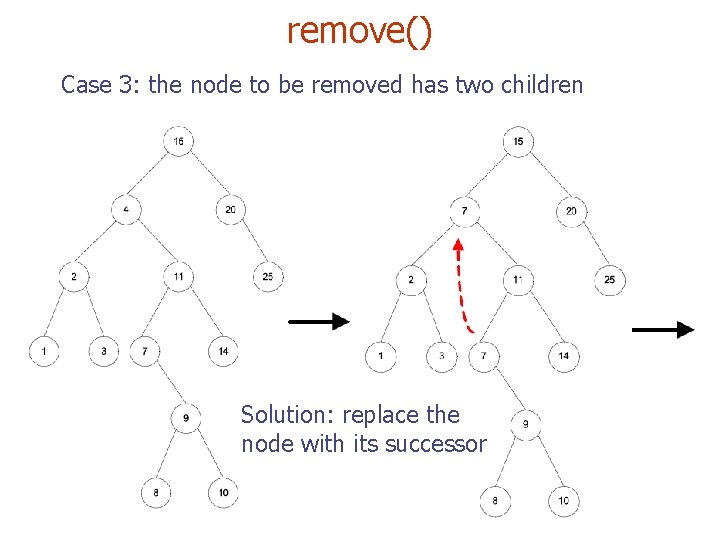
remove() Case 3: the node to be removed has two children Solution: replace the node with its successor

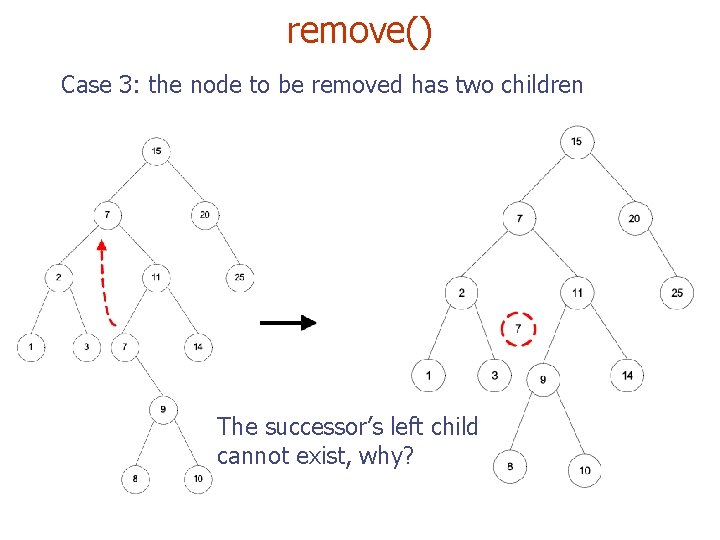
remove() Case 3: the node to be removed has two children The successor’s left child cannot exist, why?

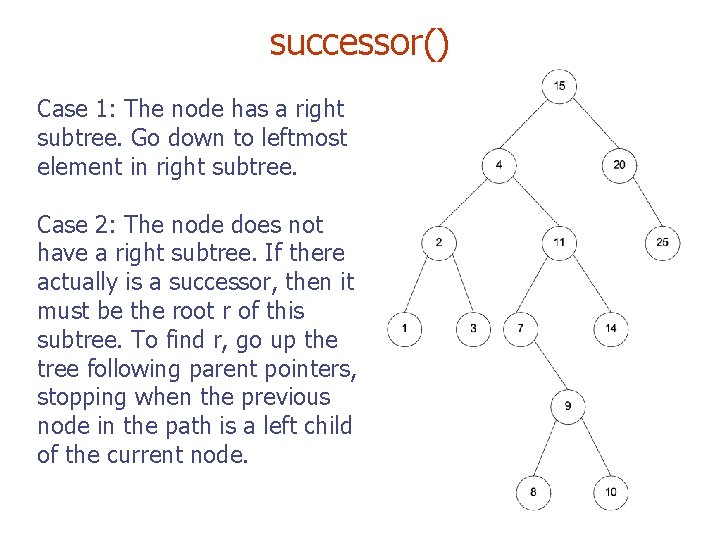
successor() Case 1: The node has a right subtree. Go down to leftmost element in right subtree. Case 2: The node does not have a right subtree. If there actually is a successor, then it must be the root r of this subtree. To find r, go up the tree following parent pointers, stopping when the previous node in the path is a left child of the current node.

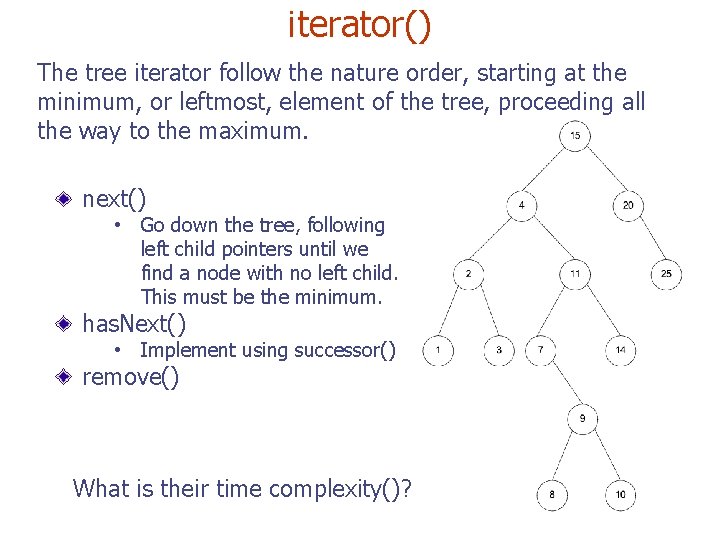
iterator() The tree iterator follow the nature order, starting at the minimum, or leftmost, element of the tree, proceeding all the way to the maximum. next() • Go down the tree, following left child pointers until we find a node with no left child. This must be the minimum. has. Next() • Implement using successor() remove() What is their time complexity()?