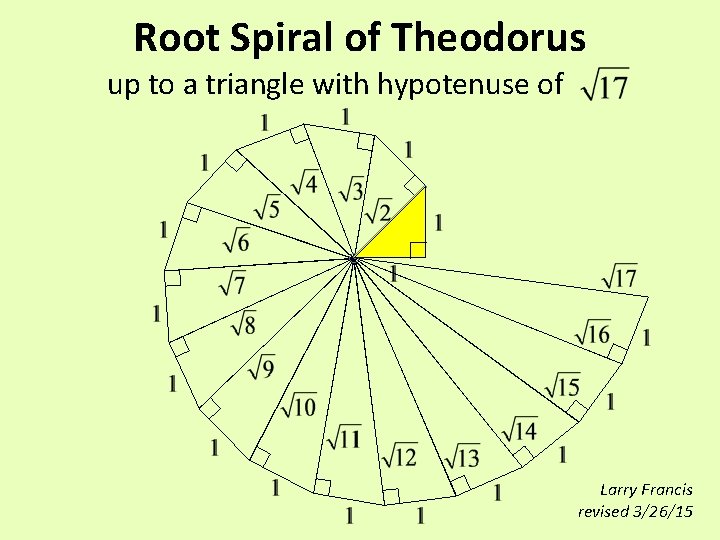
Root Spiral of Theodorus up to a triangle





- Slides: 26

Root Spiral of Theodorus up to a triangle with hypotenuse of Larry Francis revised 3/26/15

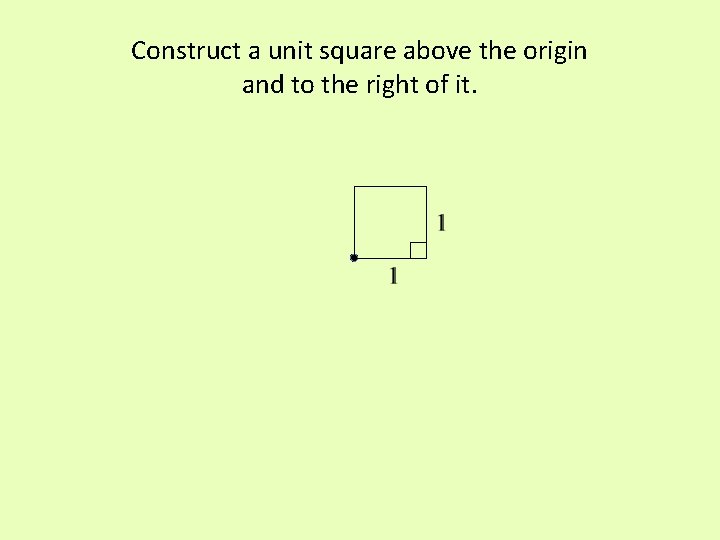
Start at a point; call it the origin.

Construct a unit square above the origin and to the right of it.

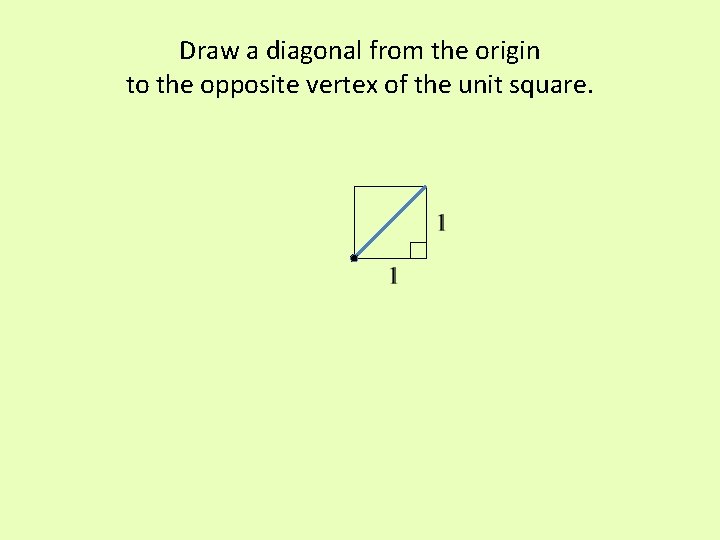
Draw a diagonal from the origin to the opposite vertex of the unit square.

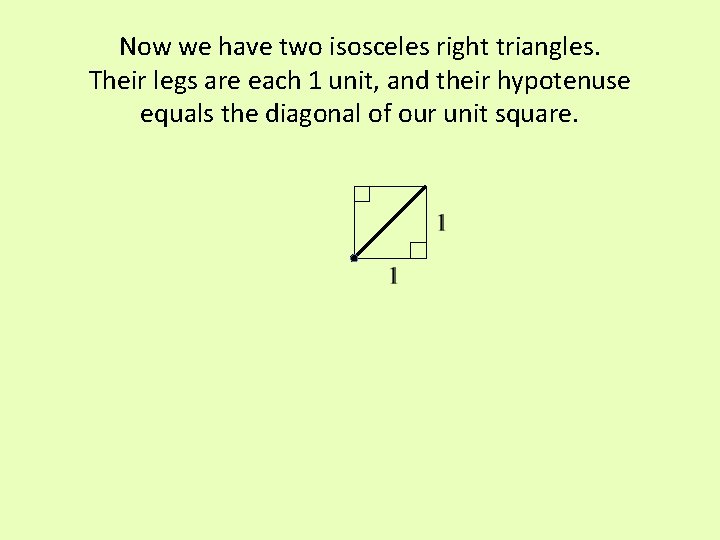
Now we have two isosceles right triangles. Their legs are each 1 unit, and their hypotenuse equals the diagonal of our unit square.

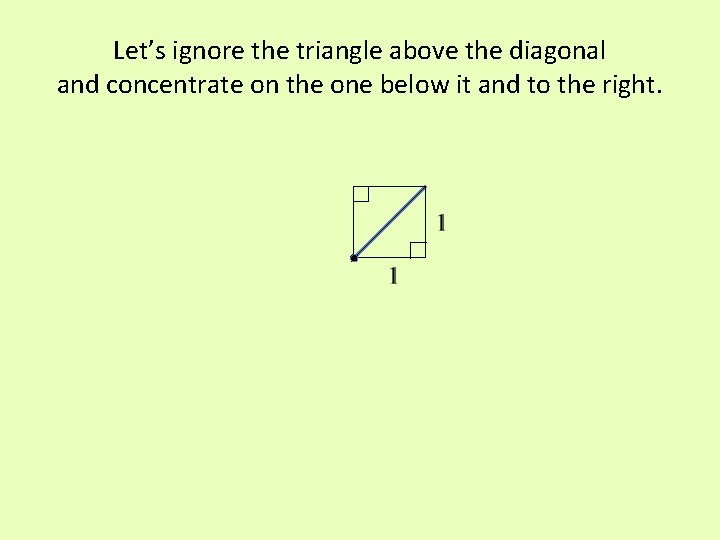
Let’s ignore the triangle above the diagonal and concentrate on the one below it and to the right.

By the Pythagorean Theorem, the length of the hypotenuse (the diagonal of our unit square) is.

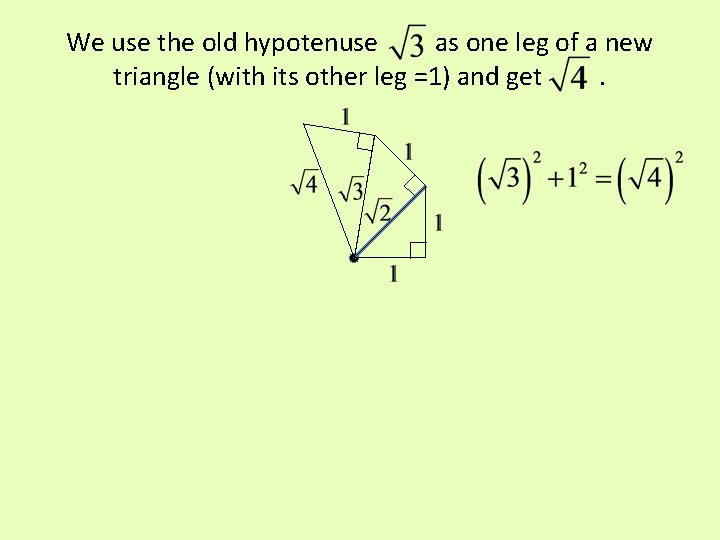
We can get by using the old hypotenuse as the long leg for a new right triangle with the short leg = 1.

We use the old hypotenuse as one leg of a new triangle (with its other leg =1) and get.

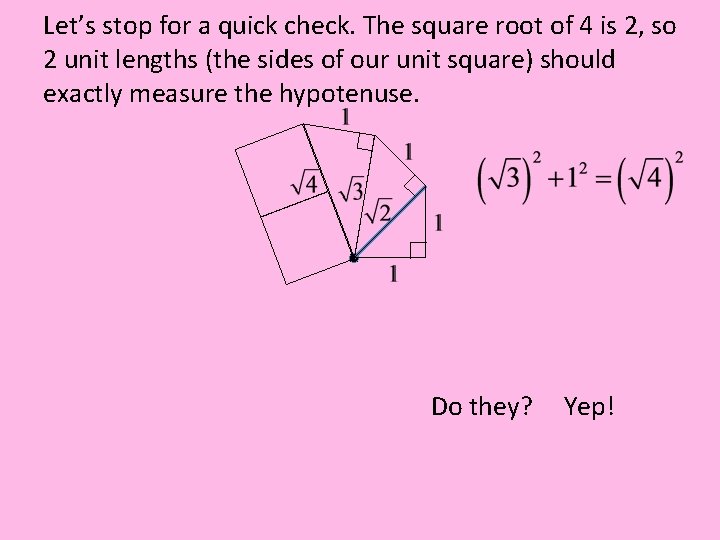
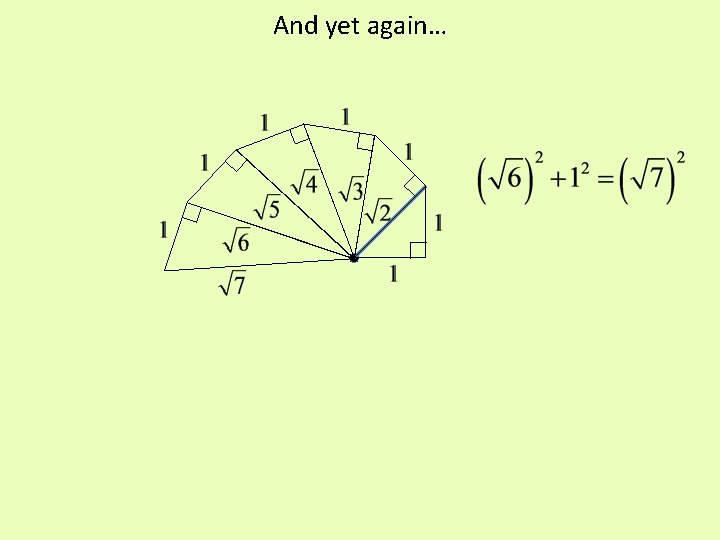
Let’s stop for a quick check. The square root of 4 is 2, so 2 unit lengths (the sides of our unit square) should exactly measure the hypotenuse. Do they? Yep!

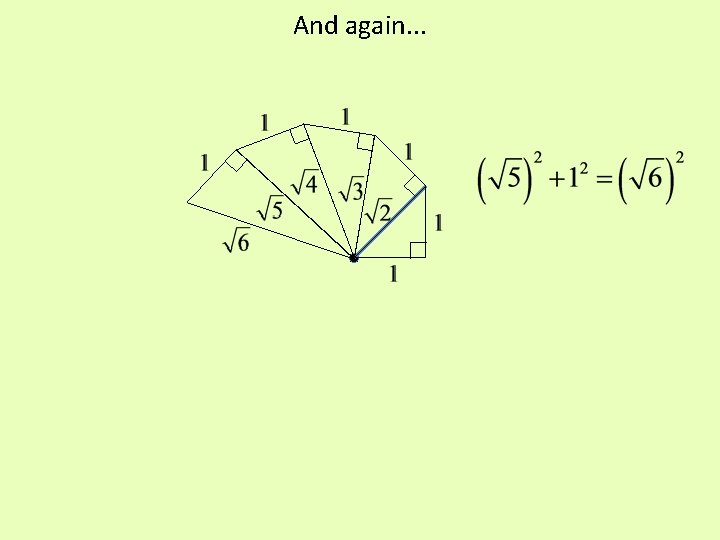
We use the old hypotenuse again for the new long leg and get the next square root.

And again. . .

And yet again…

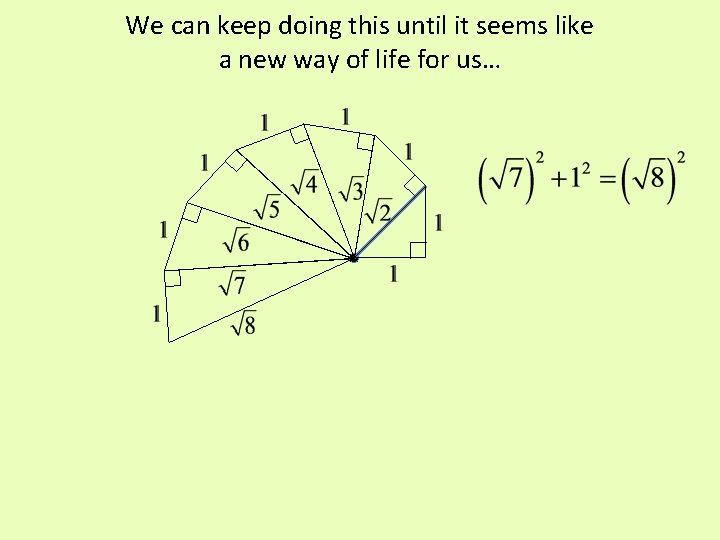
We can keep doing this until it seems like a new way of life for us…

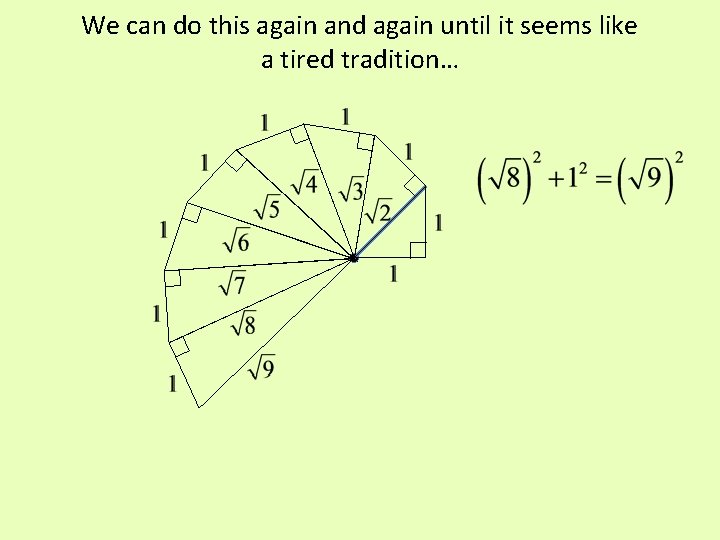
We can do this again and again until it seems like a tired tradition…

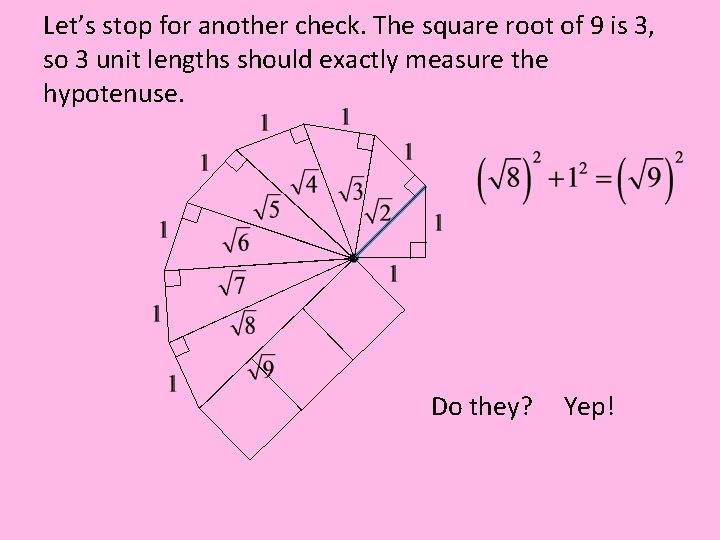
Let’s stop for another check. The square root of 9 is 3, so 3 unit lengths should exactly measure the hypotenuse. Do they? Yep!

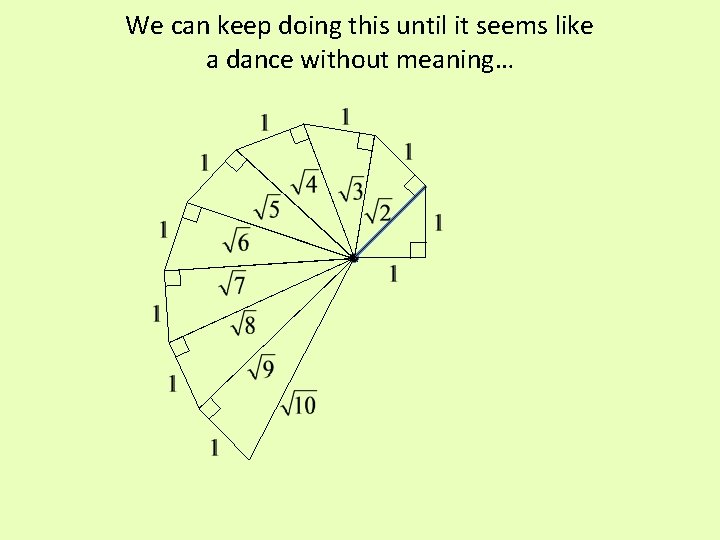
We can keep doing this until it seems like a dance without meaning…

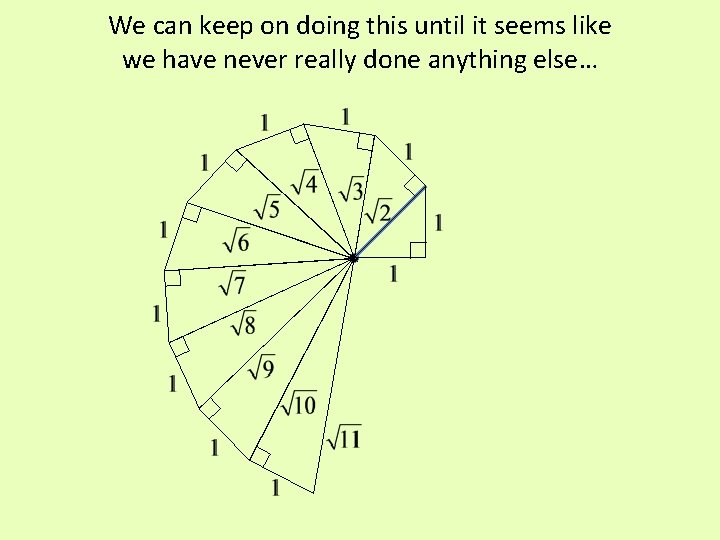
We can keep on doing this until it seems like we have never really done anything else…

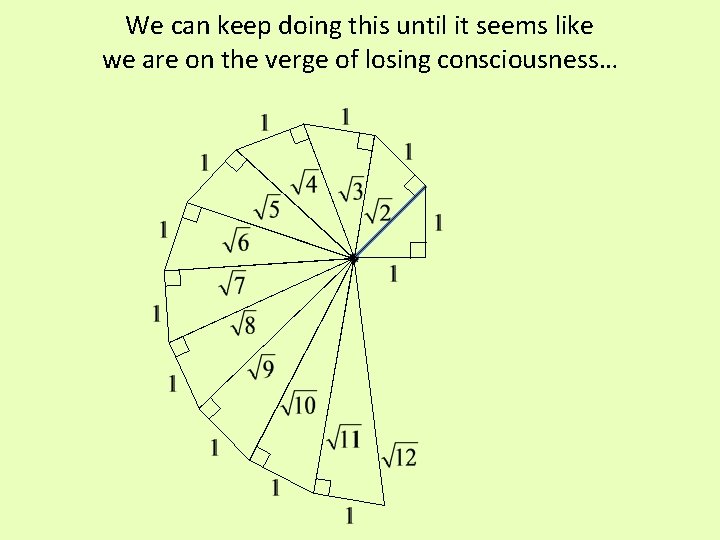
We can keep doing this until it seems like we are on the verge of losing consciousness…

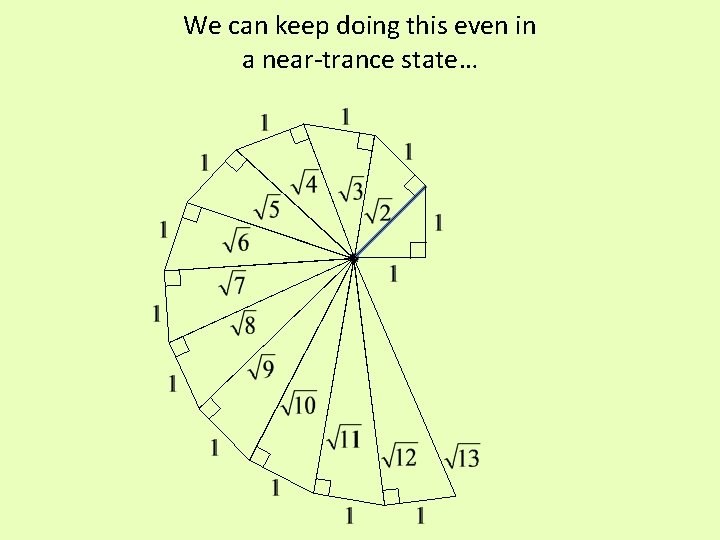
We can keep doing this even in a near-trance state…

We can keep doing this even as we feel ourselves slipping into a coma…

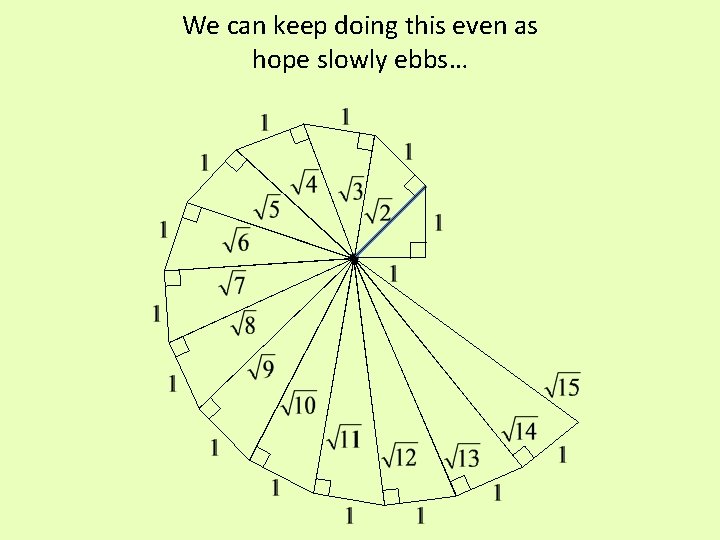
We can keep doing this even as hope slowly ebbs…

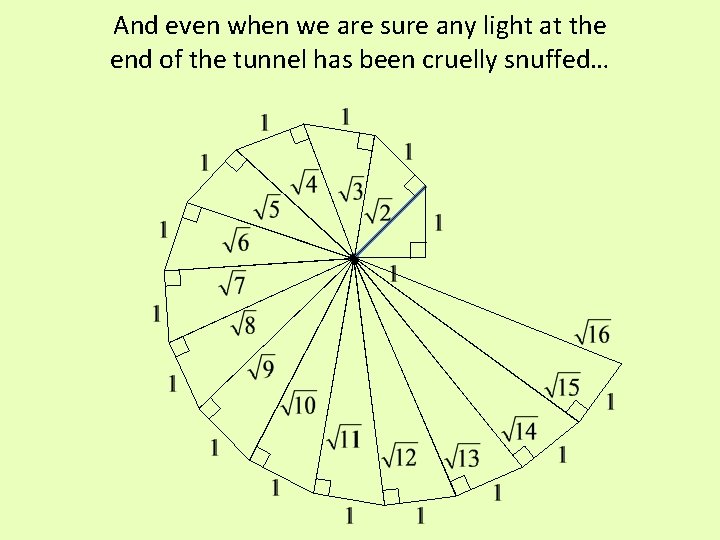
And even when we are sure any light at the end of the tunnel has been cruelly snuffed…

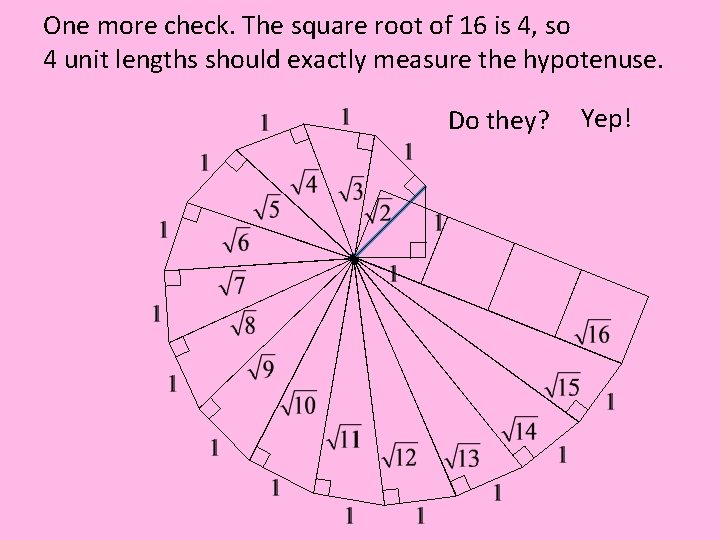
One more check. The square root of 16 is 4, so 4 unit lengths should exactly measure the hypotenuse. Do they? Yep!

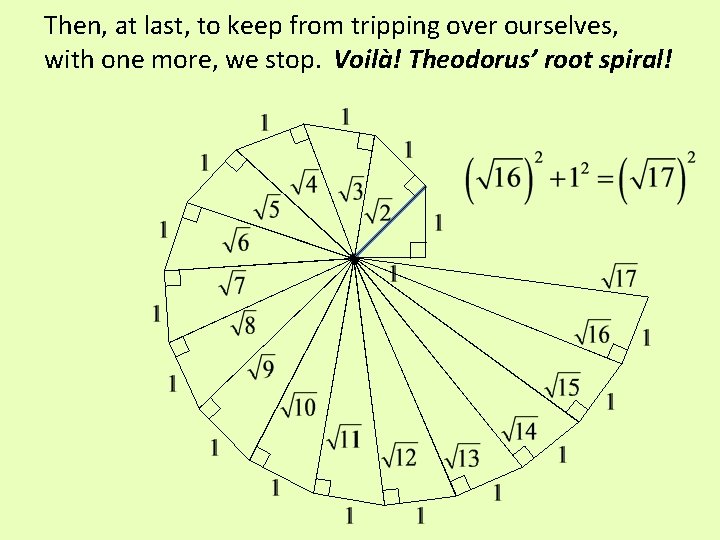
Then, at last, to keep from tripping over ourselves, with one more, we stop. Voilà! Theodorus’ root spiral!

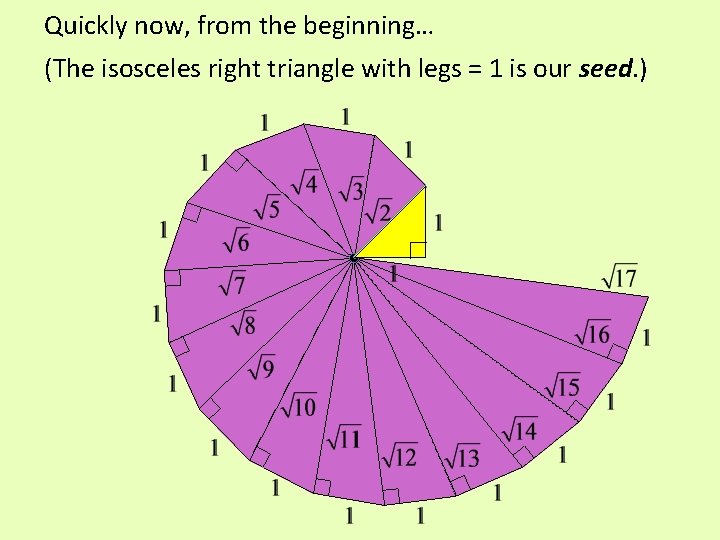
Quickly now, from the beginning… (The isosceles right triangle with legs = 1 is our seed. )