Root Mean Square Velocity urms urms 3 RTM

Root Mean Square Velocity (urms) urms = √(3 RT/M) • R = 8. 3145 J/K(mol) • T = temp in KELVIN • M = mass of one mole in KILOGRAMS (use the molar mass from the periodic table and convert to kg/mol)

RMS Example • Calculate the root mean square velocity for the atoms in a sample of oxygen gas at 0ºC. • Answer: 461 m/s • At 300ºC • Answer: 668 m/s

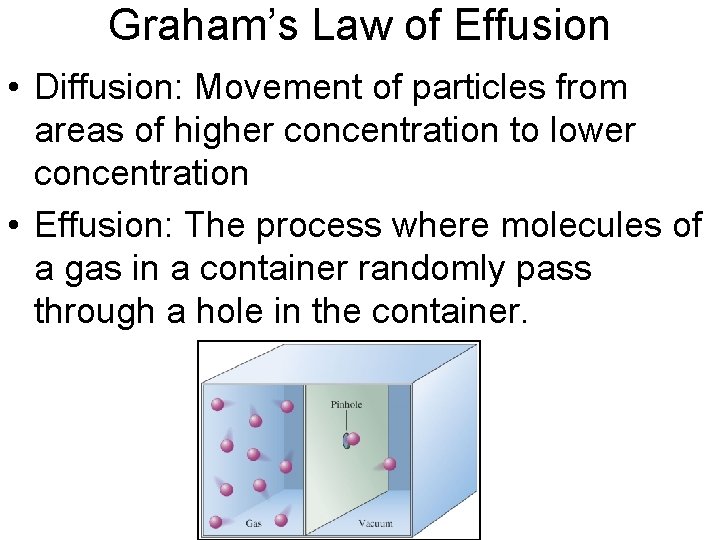
Graham’s Law of Effusion • Diffusion: Movement of particles from areas of higher concentration to lower concentration • Effusion: The process where molecules of a gas in a container randomly pass through a hole in the container.

Graham’s Law of Effusion Rate of Effusion for gas 1 = √M 2 Rate of Effusion for gas 2 √ M 1 M = molar masses of the gases Example 1: Compare the rate of effusion of carbon dioxide with that of hydrogen chloride at the same temperature and pressure. Answer: CO 2 effuses 0. 9 X as fast as HCl.

Example #2 If a molecule of neon gas travels at an average of 400 m/s at a given temp. , estimate the average speed of a molecule of butane gas, C 4 H 10, at the same temp. Answer: 235 m/s

Summary… Larger GFM = slower rate of effusion.

Real Gases • No gas actually follows the ideal gas law • Some close at low pressures and/or high temperatures • Under certain conditions (see above), gases behave more like ideal gases

Van der Waals Equation • Corrects the ideal gas equation to take nonideal conditions into account (P + n 2 a)(V-nb) = n. RT V 2 P= pressure of gas (atm) V = volume of gas (L) n = moles of gas T = temperature (K) R = 0. 08206 L(atm)/mol(K)

Defining Variables…MORE. a = a constant, different for each gas, that takes into account the attractive forces between molecules (table 5. 3 pg. 216) b = a constant, different for each gas, that takes into account the volume of each molecule (table 5. 3 pg. 216)

Example • Calculate the pressure exerted by 0. 3000 mol of He in a 0. 2000 L container at -25. 0ºC – Using the ideal gas law – Answer: 30. 53 atm – Using van der Waal’s equation – Where a = 0. 0341 and b = 0. 0237 – Answer: 31. 60 atm • You can calculate percent error: 3% – |experimental – accepted|/accepted = ___ x 100 =

Pollution and Atmospheric Gases • Your book discusses these - you can read about them at the end of chapter 5, but we will not be going over them in class…