ROMS 4 DVar Secrets Revealed Andy Moore UC





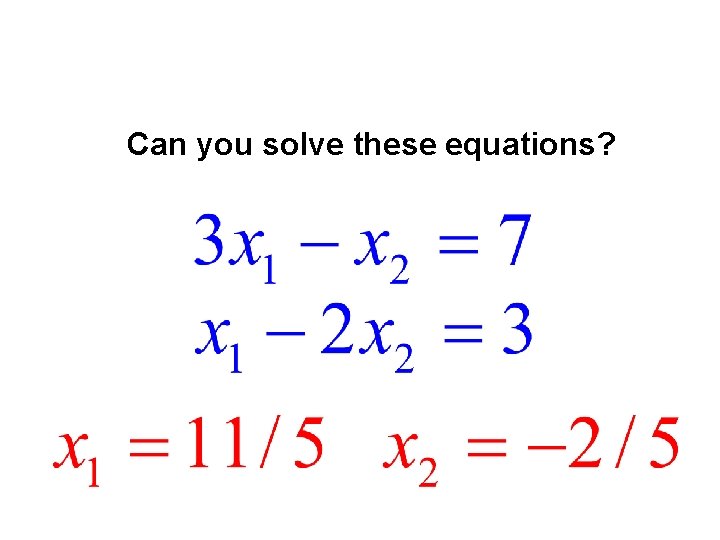
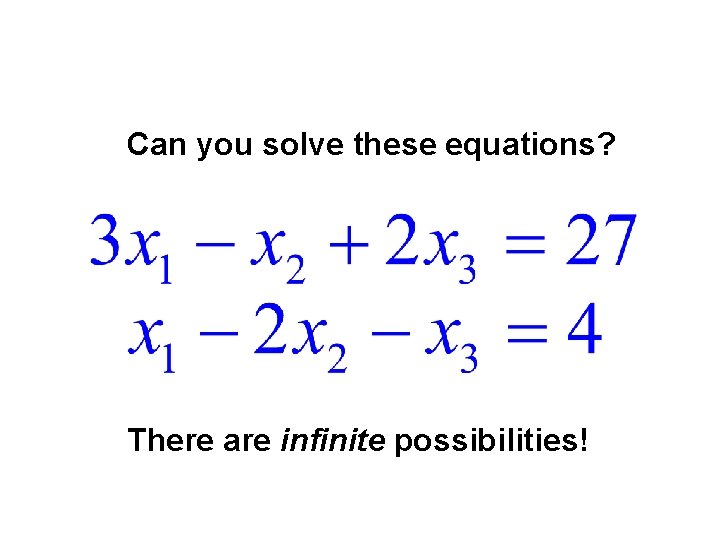




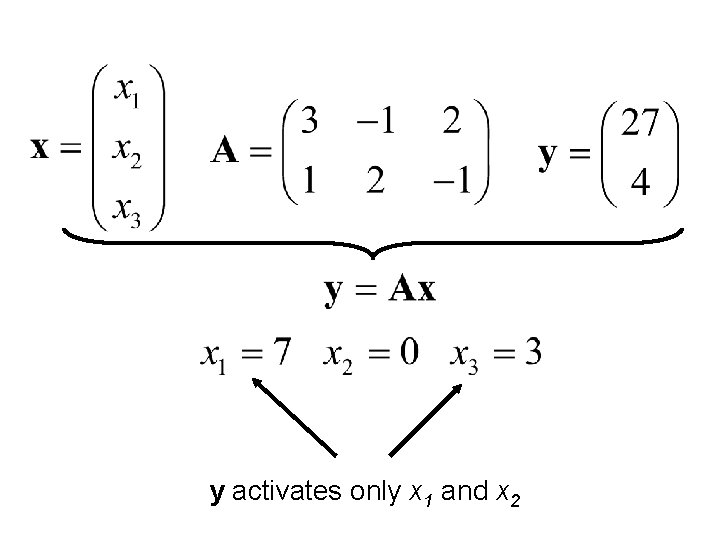










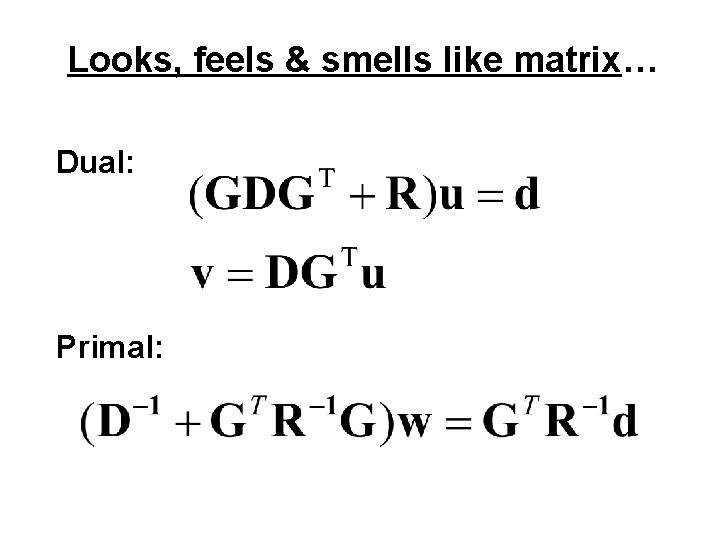




















- Slides: 70

ROMS 4 D-Var: Secrets Revealed Andy Moore UC Santa Cruz

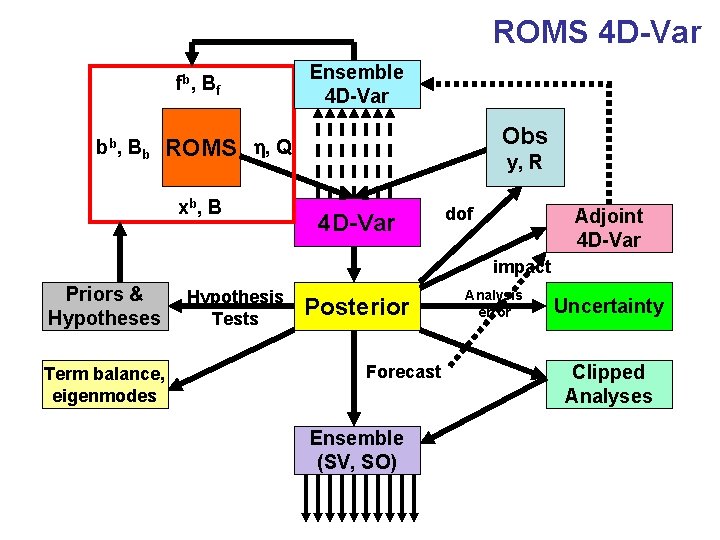
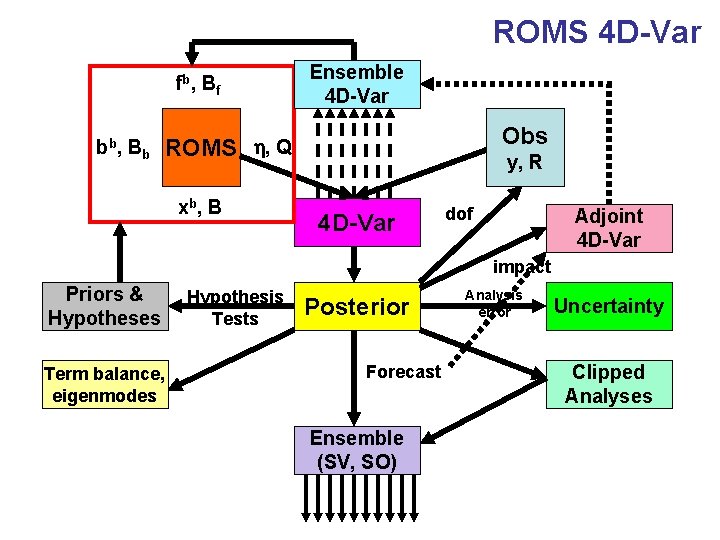
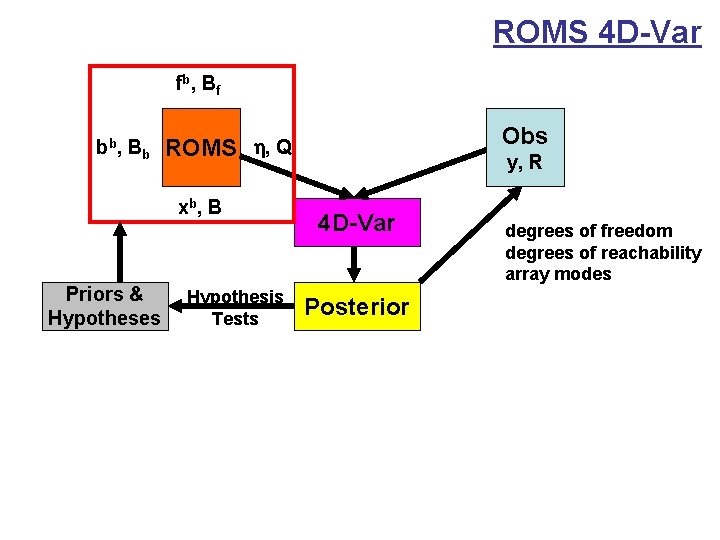
ROMS 4 D-Var fb , B f bb , B b Ensemble 4 D-Var Obs ROMS h, Q xb , B y, R 4 D-Var dof Adjoint 4 D-Var impact Priors & Hypotheses Term balance, eigenmodes Hypothesis Tests Posterior Forecast Ensemble (SV, SO) Analysis error Uncertainty Clipped Analyses

ROMS 4 D-Var • Incremental (linearize about a prior) (Courtier et al, 1994) • Primal & dual formulations (Courtier 1997) • Primal – Incremental 4 -Var (I 4 D-Var) • Dual – PSAS (4 D-PSAS) & indirect representer (R 4 DVar) (Da Silva et al, 1995; Egbert et al, 1994) • Strong and weak (dual only) constraint • Preconditioned, Lanczos formulation of conjugate gradient (Lorenc, 2003; Tshimanga et al, 2008; Fisher, 1997) • Diffusion operator model for prior covariances (Derber & Bouttier, 1999; Weaver & Courtier, 2001) • Multivariate balance for prior covariance (Weaver et al, 2005) • Physical and ecosystem components • Parallel (MPI)

The Secrets… • The adjoint operator • Matrix-less iterations • Lanczos algorithm

What is an adjoint?

Can you solve this equation?
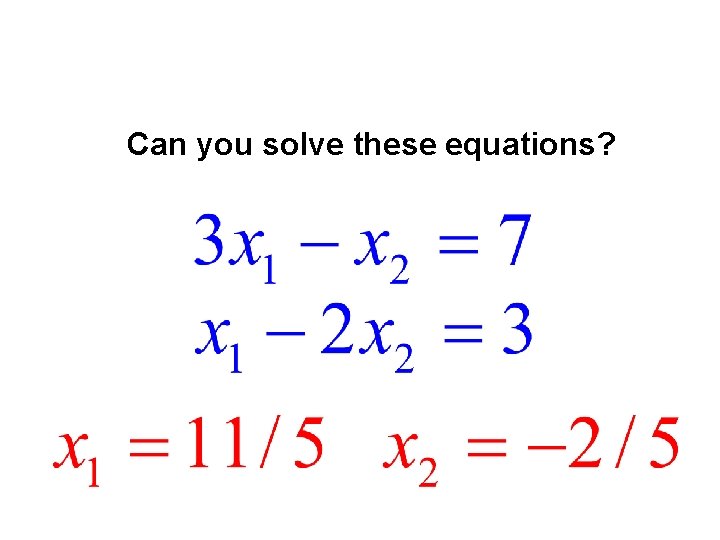
Can you solve these equations?
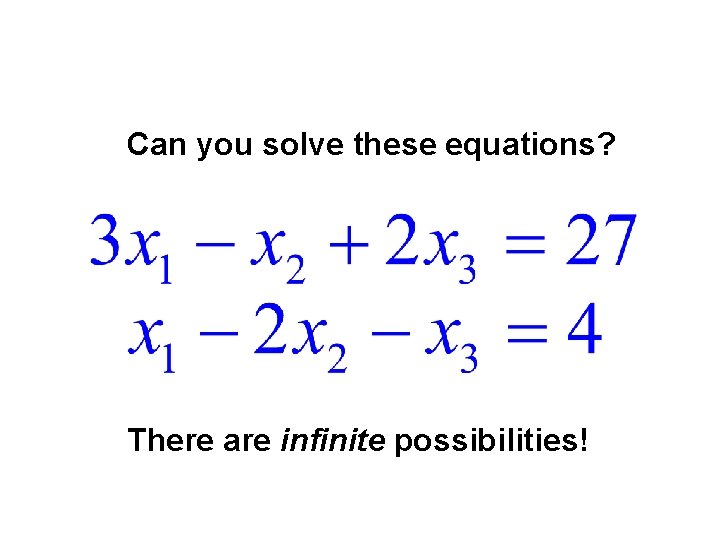
Can you solve these equations? There are infinite possibilities!

But…

…there is a Natural Solution Look for solutions of the form: Generating vector

Two Spaces A is a 2× 3 matrix y and s reside in “ 2 -space” x resides in “ 3 -space” A maps from 3 -space to 2 -space AT is a 3× 2 matrix AT maps from 2 -space to 3 -space Identifies the part of 3 -space that is activated by y

This looks lot like the ocean state estimation problem… Think of x as corrections to the prior/background Ocean Observations Ocean state Insufficient observations to uniquely determine elements of x Use AT to identify the natural solution
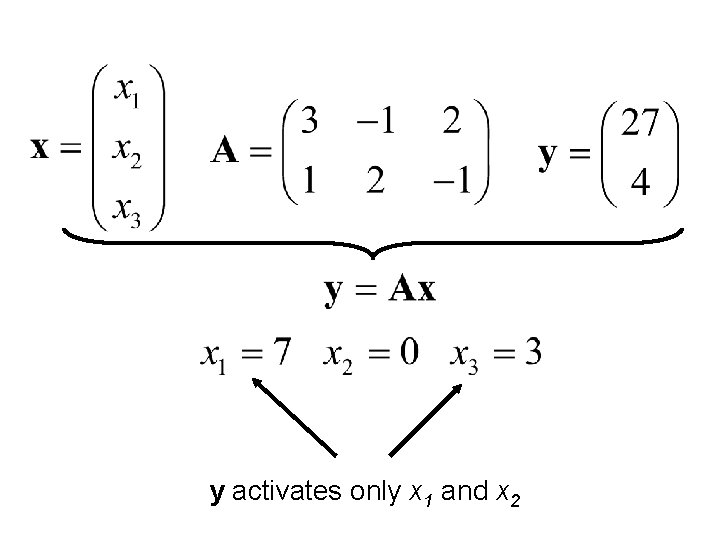
y activates only x 1 and x 2

The Adjoint

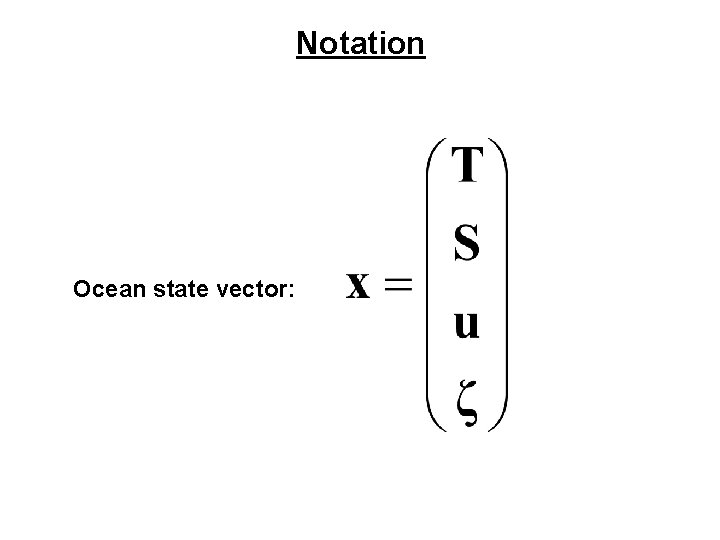
Notation Ocean state vector:

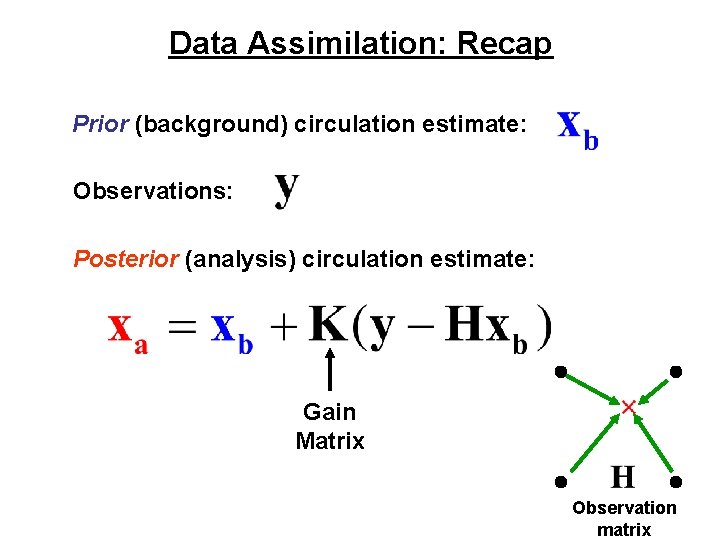
Data Assimilation: Recap Prior (background) circulation estimate: Observations: Posterior (analysis) circulation estimate: Gain Matrix Observation matrix

Data Assimilation: Recap Posterior (analysis) circulation estimate: Innovation vector: Adjoint plays a key role in identifying K

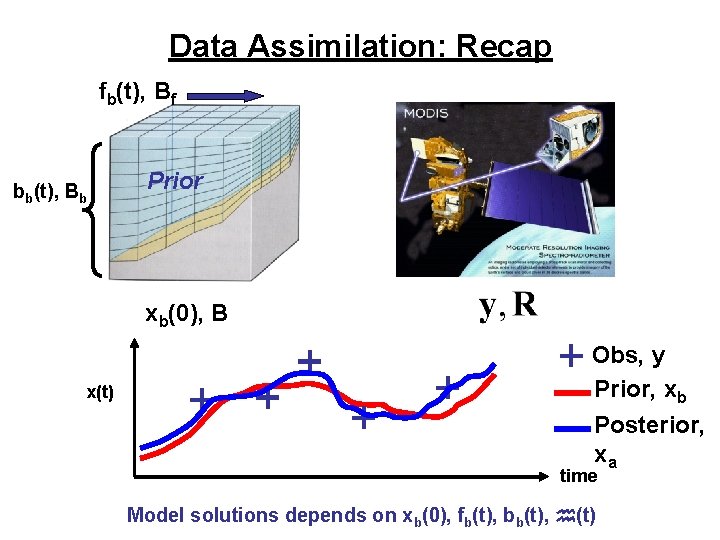
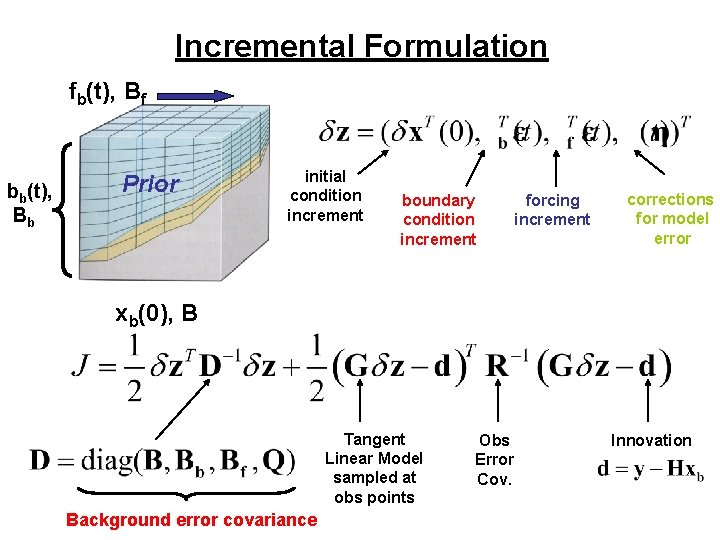
Data Assimilation: Recap fb(t), Bf bb(t), Bb Prior xb(0), B x(t) Obs, y Prior, xb Posterior, xa time Model solutions depends on xb(0), fb(t), bb(t), h(t)

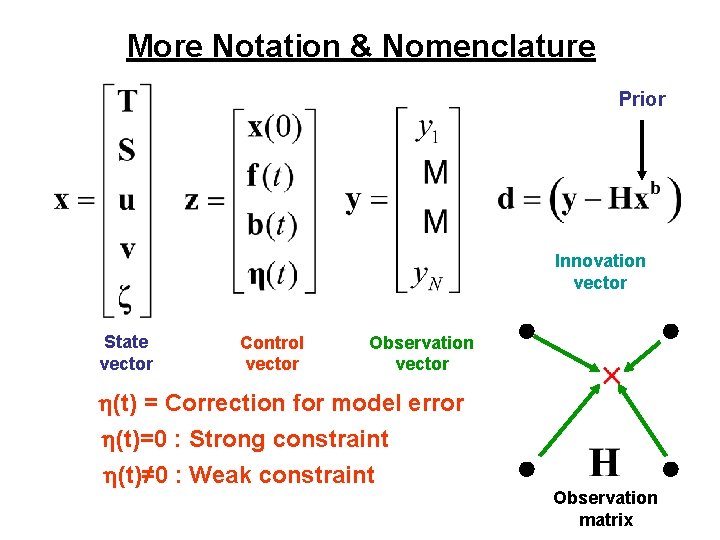
More Notation & Nomenclature Prior Innovation vector State vector Control vector Observation vector h(t) = Correction for model error h(t)=0 : Strong constraint h(t)≠ 0 : Weak constraint Observation matrix

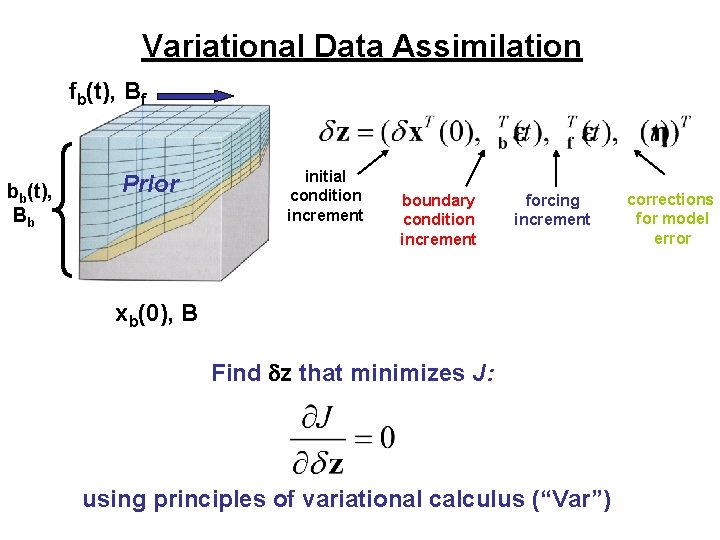
Variational Data Assimilation: Recap Conditional Probability: Observation error covariance Background error covariance J is called the “cost” or “penalty” function. Problem: Find z=za that minimizes J (i. e. maximizes P) za is the “maximum likelihood” or “minimum variance” estimate.

Incremental Formulation fb(t), Bf bb(t), Bb Prior initial condition increment boundary condition increment forcing increment corrections for model error xb(0), B Tangent Linear Model sampled at obs points Background error covariance Obs Error Cov. Innovation

Two Spaces G samples the tangent linear model at observation points. G maps from model (primal) space to observation (dual) space GT maps from observation (dual) space to model (primal) space

Variational Data Assimilation fb(t), Bf bb(t), Bb Prior initial condition increment boundary condition increment forcing increment xb(0), B Find dz that minimizes J: using principles of variational calculus (“Var”) corrections for model error

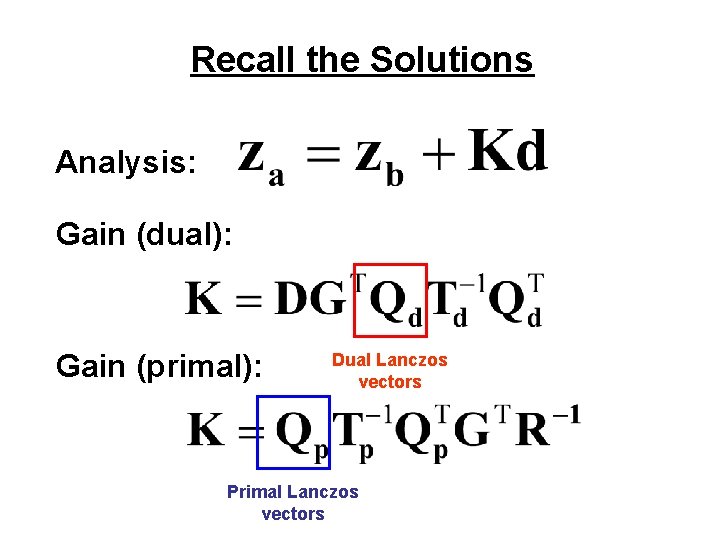
The Solution! Analysis: Gain (dual): Gain (primal):

Two Spaces Gain (dual): Gain (primal):

Two Spaces G maps from model (primal) space to observation (dual) space GT maps from observation (dual) space to model (primal) space

Recall the Solutions Analysis: Gain (dual): Gain (primal):

Equivalent Linear Systems Dual: Primal:

Iterative Solution of Linear Equations General form: Find s that minimizes: At the minimum:

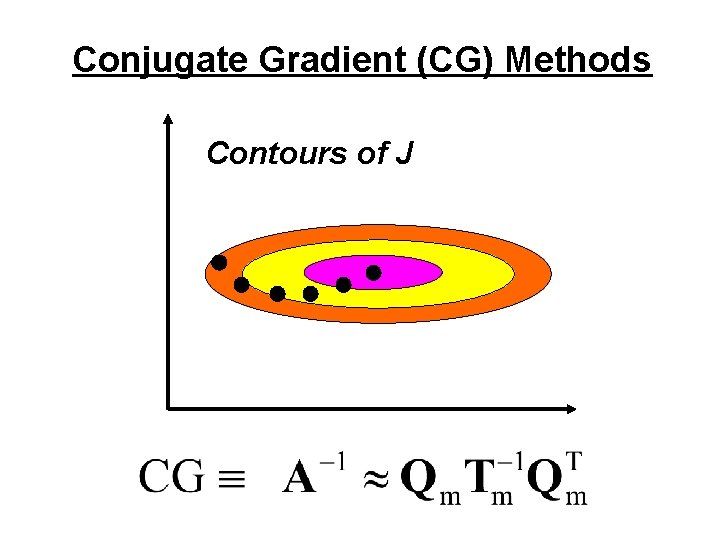
Conjugate Gradient (CG) Methods Contours of J
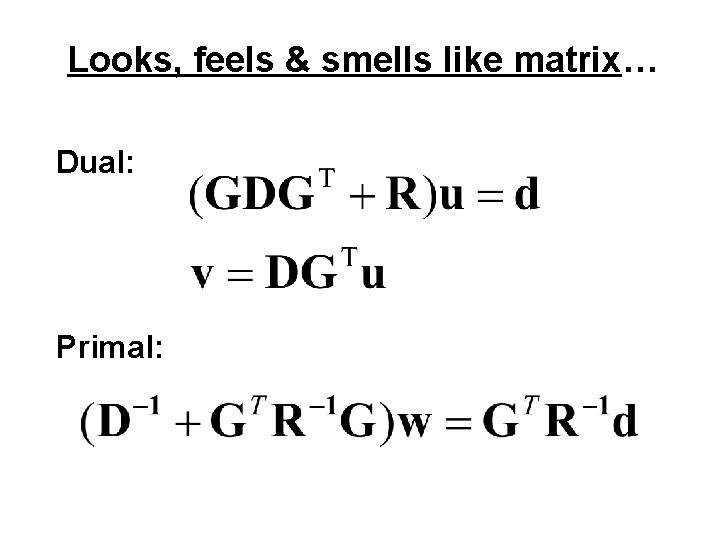
Looks, feels & smells like matrix… Dual: Primal:

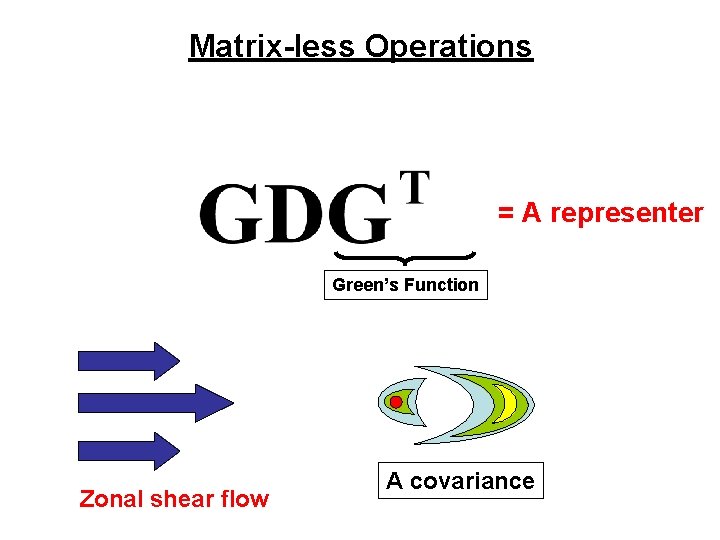
Matrix-less Operations There are no matrix multiplications! Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Adjoint Model Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Adjoint Model Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Adjoint Model Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Covariance Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Covariance Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Tangent Linear Model Zonal shear flow

Matrix-less Operations There are no matrix multiplications! Tangent Linear Model Zonal shear flow

Matrix-less Operations = A representer Green’s Function Zonal shear flow A covariance

Matrix-less Operations There are no matrix multiplications! Tangent Linear Model Zonal shear flow

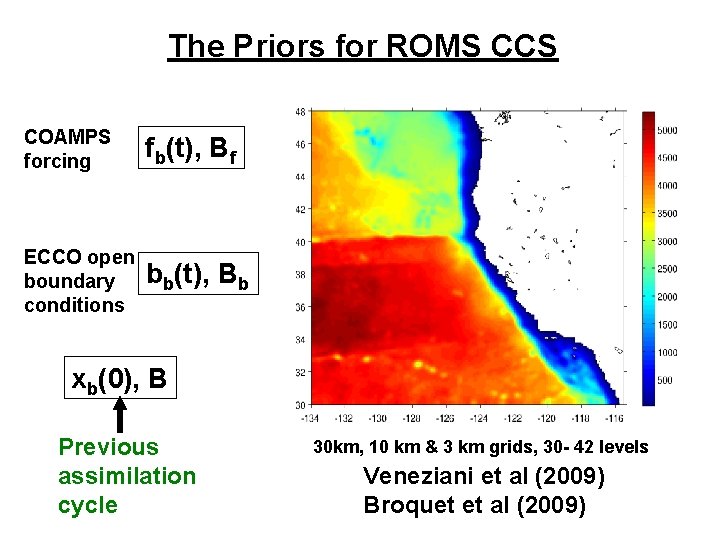
The Priors for ROMS CCS COAMPS forcing fb(t), Bf ECCO open boundary conditions bb(t), Bb xb(0), B Previous assimilation cycle 30 km, 10 km & 3 km grids, 30 - 42 levels Veneziani et al (2009) Broquet et al (2009)

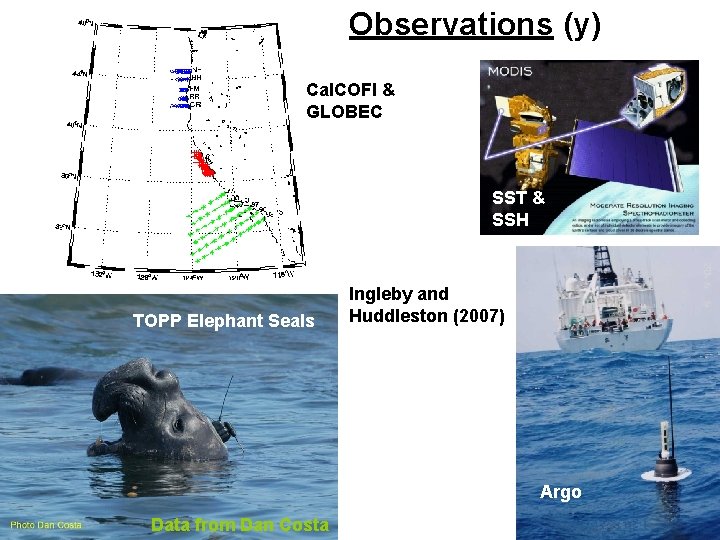
Observations (y) Cal. COFI & GLOBEC SST & SSH TOPP Elephant Seals Ingleby and Huddleston (2007) Argo Data from Dan Costa

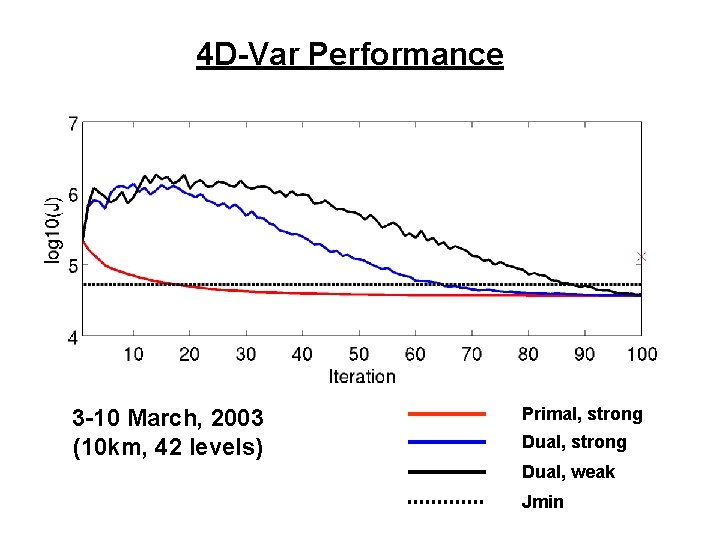
4 D-Var Performance 3 -10 March, 2003 (10 km, 42 levels) Primal, strong Dual, weak Jmin

The Beauty of Lanczos Cornelius Lanczos (1893 -1974)

Conjugate Gradient (CG) Methods Contours of J

Recall the Solutions Analysis: Gain (dual): Gain (primal): Dual Lanczos vectors Primal Lanczos vectors


Endless Possibilties? • Posterior error • Posterior EOFs • Preconditioning • Degrees of freedom • Array modes • Observation impact • Observation sensitivity • Think outside the box…

ROMS 4 D-Var fb , B f bb , B b Ensemble 4 D-Var Obs ROMS h, Q xb , B y, R 4 D-Var dof Adjoint 4 D-Var impact Priors & Hypotheses Term balance, eigenmodes Hypothesis Tests Posterior Forecast Ensemble (SV, SO) Analysis error Uncertainty Clipped Analyses

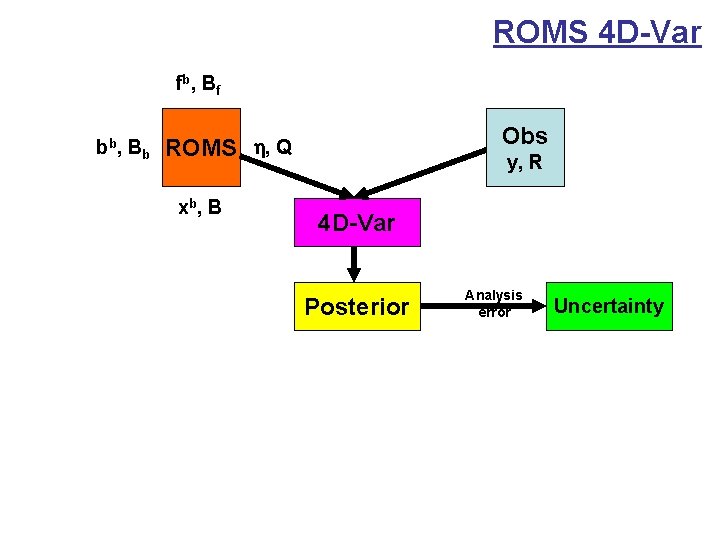
ROMS 4 D-Var fb , B f bb , B b Obs ROMS h, Q xb , B y, R 4 D-Var Posterior Analysis error Uncertainty

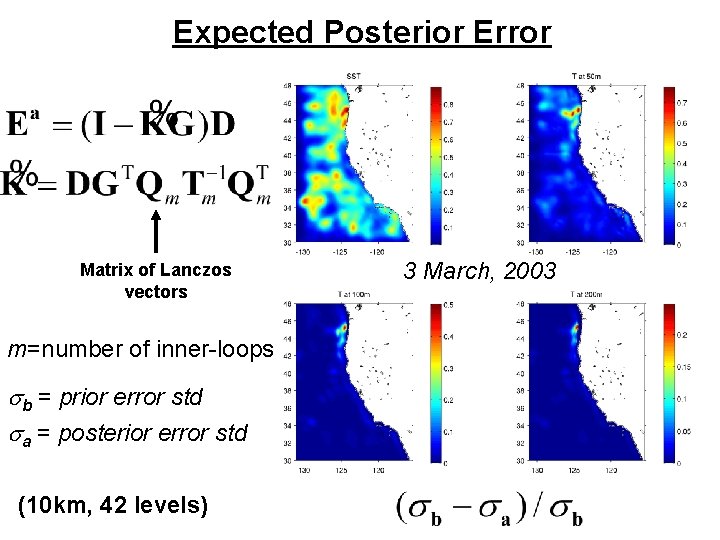
Expected Posterior Error Matrix of Lanczos vectors m=number of inner-loops sb = prior error std sa = posterior error std (10 km, 42 levels) 3 March, 2003

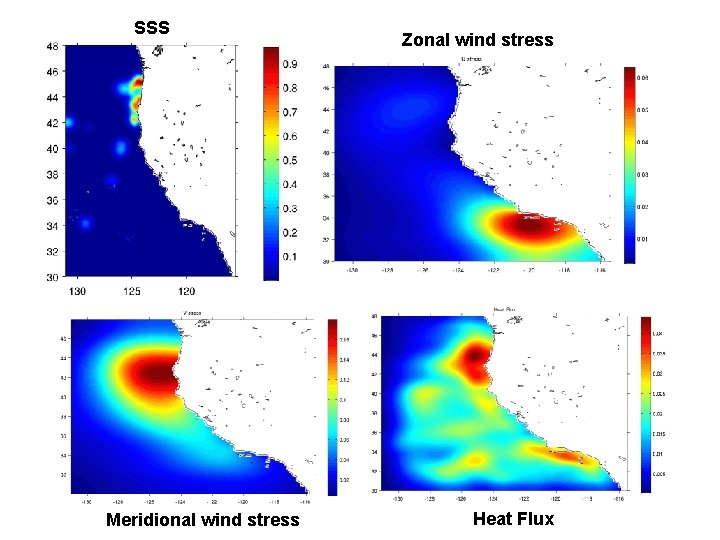
SSS Meridional wind stress Zonal wind stress Heat Flux

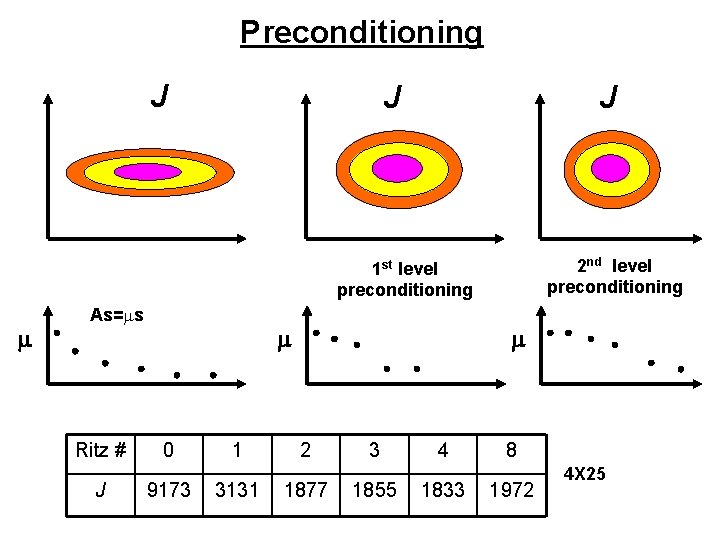
Preconditioning J J J 2 nd level preconditioning 1 st level preconditioning m As=ms Ritz # J m 0 9173 1 3131 m 2 1877 3 1855 4 1833 8 1972 4 X 25

ROMS 4 D-Var fb , B f bb , B b xb , B Priors & Hypotheses Obs ROMS h, Q Hypothesis Tests y, R 4 D-Var Posterior degrees of freedom degrees of reachability array modes

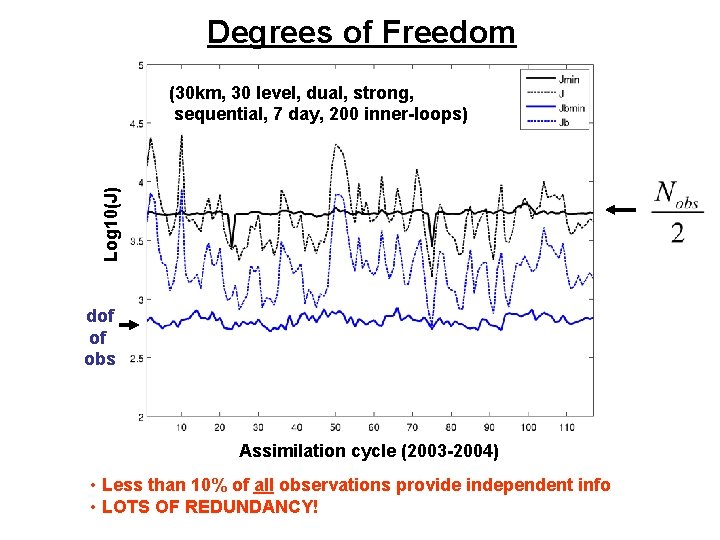
Degrees of Freedom Recall that the optimal increments minimize: Theoretical min: No. of dof in obs No. of dof in prior “dof” – degrees of freedom (Bennett et al, 1993; Cardinali et al, 2004; Desroziers et al. , 2009)

Degrees of Freedom Log 10(J) (30 km, 30 level, dual, strong, sequential, 7 day, 200 inner-loops) dof of obs Assimilation cycle (2003 -2004) • Less than 10% of all observations provide independent info • LOTS OF REDUNDANCY!

Degrees of Freedom Degrees of freedom in the obs: But: So:

Degrees of Freedom Degrees of freedom in the obs: But: So:

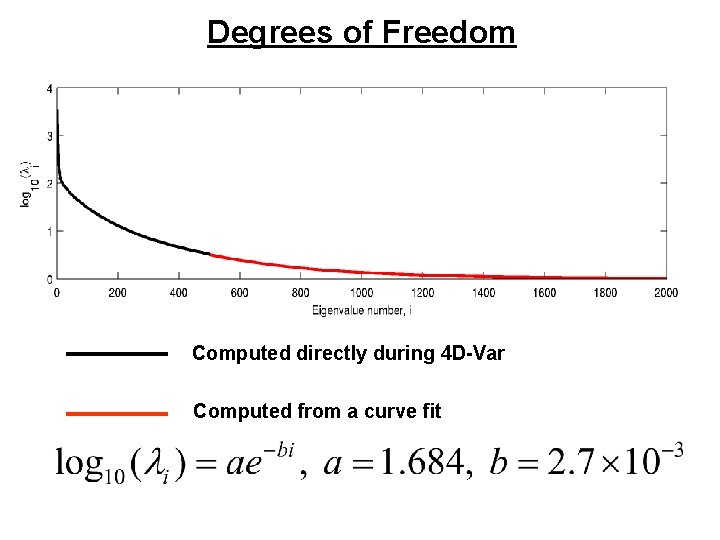
Degrees of Freedom Computed directly during 4 D-Var Computed from a curve fit

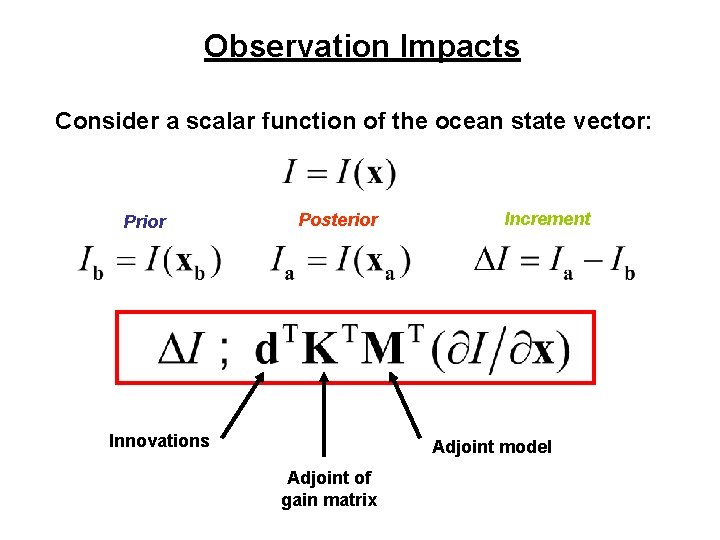
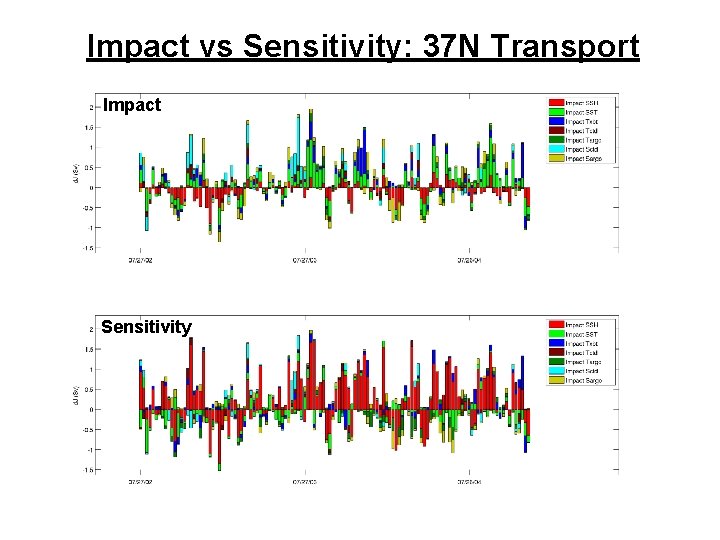
Observation Impacts Consider a scalar function of the ocean state vector: Prior Posterior Innovations Increment Adjoint model Adjoint of gain matrix

Observation Impacts But: So:

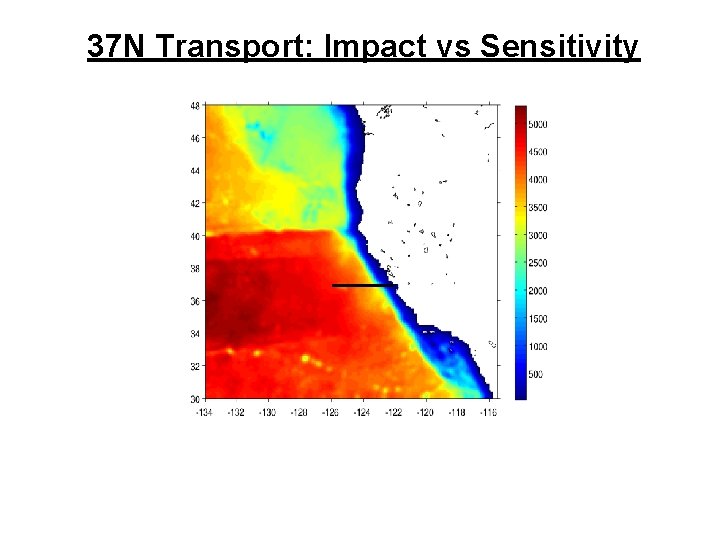
Observation Sensitivity The gain matrix is actually a nonlinear function of d: Consider variations in the observation vector dy: Linearization of 4 D-Var Relationship to obs impact: e. g. : 37 N transport Adjoint of 4 D-Var

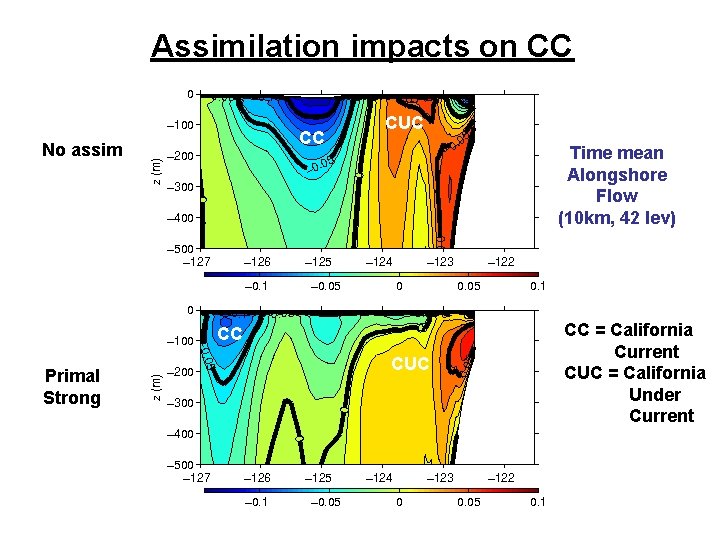
Assimilation impacts on CC CC No assim CUC Time mean Alongshore Flow (10 km, 42 lev) CC Primal Strong CUC CC = California Current CUC = California Under Current

37 N Transport: Impact vs Sensitivity

Impact vs Sensitivity: 37 N Transport Impact Sensitivity

Two Spaces: Obs Impact maps from observation (dual) space to model (primal) space maps from model (primal) space to observation (dual) space Identifies the part of model space that controls 37 N transport and that is activated by the observations

Two Spaces: Obs Sensitivity maps from observation (dual) space to model (primal) space maps from model (primal) space to observation (dual) space Identifies the part of model space that controls 37 N transport and that is activated by the observations during 4 D-Var

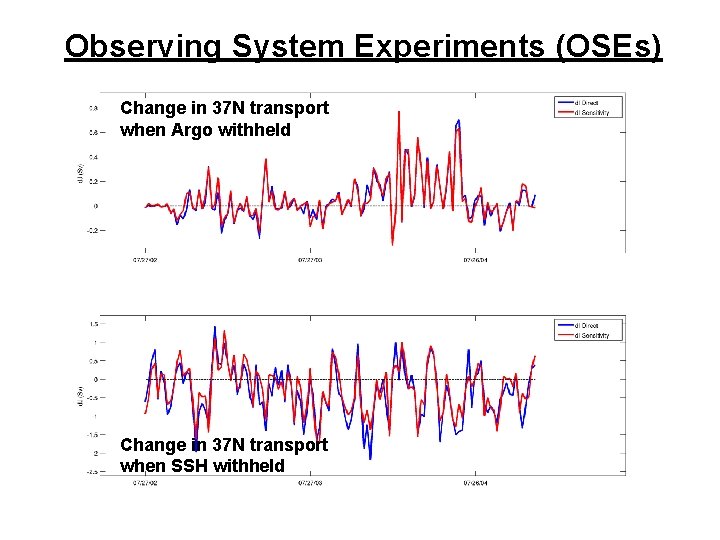
Observing System Experiments (OSEs) Change in 37 N transport when Argo withheld Change in 37 N transport when SSH withheld

Summary Most of the power and utility of modern data assimilation systems is possible because of: • The adjoint operator • Matrix-less iterations • Lanczos algorithm