Rolling Tachyon and Vacuum Super String Field Theory

Rolling Tachyon and Vacuum Super. String Field Theory I. Ya. Aref'eva Steklov Mathematical Institute Based on : I. A. , D. Belov, A. Giryavets, A. Koshelev, hep-th/0112214, hep-th/0201197, hep-th/0203227, hep-th/0204239 and

OUTLOOK • Cubic SSFT action • Tachyon Condensation in SSFT • Rolling Tachyon i) Field theory (anharmonic oscillator) ii) corrections iii) p-adic strings iv) SFT • Vacuum Super. String Field Theory i) New BRST charge ii) Special solutions - sliver, lump, etc. : algebraic; surface states; Moyal representation iii) Time dependence • Conclusion

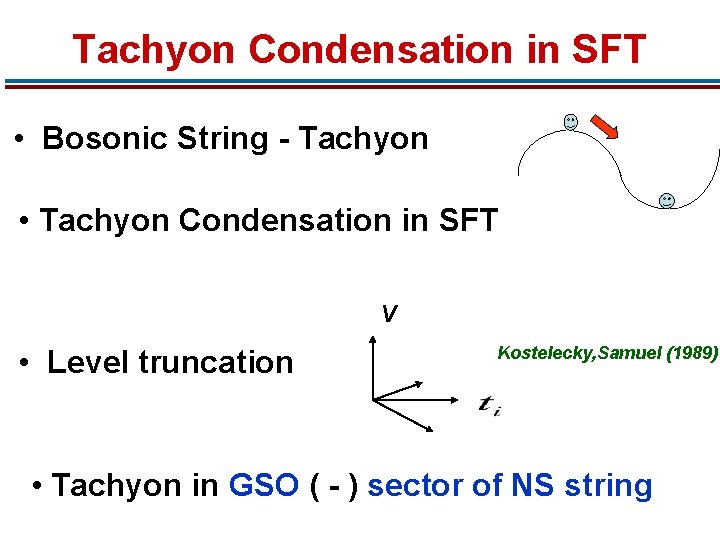
Tachyon Condensation in SFT • Bosonic String - Tachyon • Tachyon Condensation in SFT V • Level truncation Kostelecky, Samuel (1989) • Tachyon in GSO ( - ) sector of NS string

String Field Theory on a non-BPS brane I. A. , Belov, Koshelev, Medvedev(2001) E. Witten (1986) Parity odd even GSO + - I. A. , Medvedev, Zubarev (1990) Preitschopf, Thorn, Yost (1990)

Vertex operators in pictures – 1 and 0 Level GSO 0 1/2 1 3/2 2 + + + Name Picture -1 u t r s Picture 0 - Berkovits (1995) N. B. , Sen, Zwiebach (2000) I. A. , Belov, Koshelev, P. M. (2001)

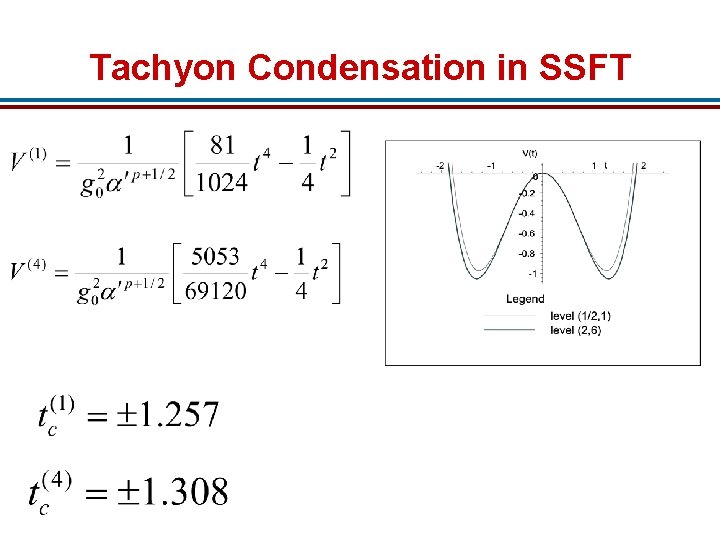
Tachyon Condensation in SSFT

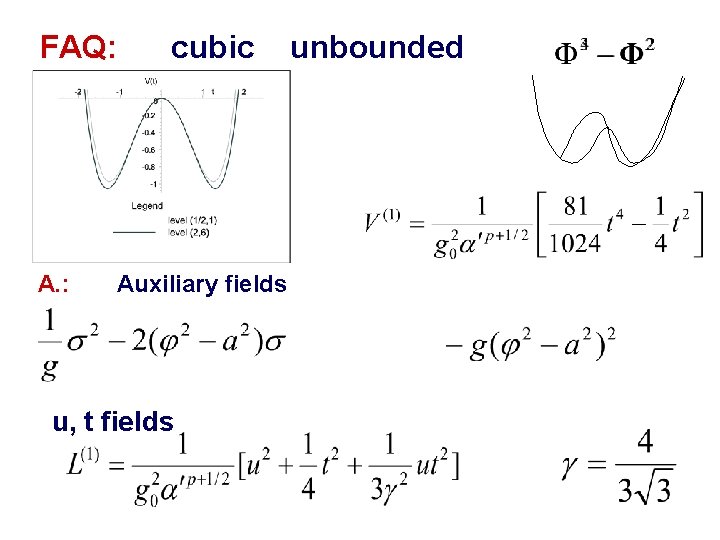
FAQ: A. : cubic Auxiliary fields u, t fields unbounded

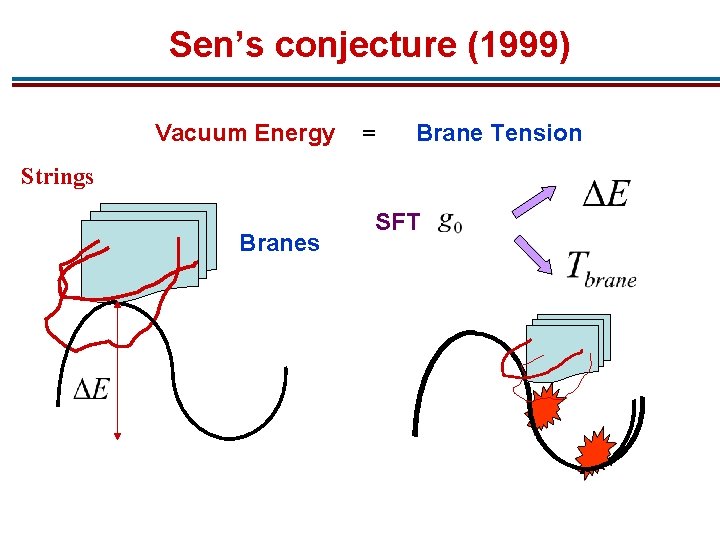
Sen’s conjecture (1999) Vacuum Energy = Brane Tension Strings Branes SFT

Sen’s conjectures (1999) 97. 5% = Our calculations: 105. 8% NO OPEN STRING EXCITATIONS CLOSED STRING EXCITATIONS

Rolling Tachyon • • • Anharmonic oscillator Alpha ‘ corrections p-adic strings SFT (for bosonic string Sen, hep-th/0203211) SSFT for non-BPS branes

Anharmonic oscillator If resonance i. e.

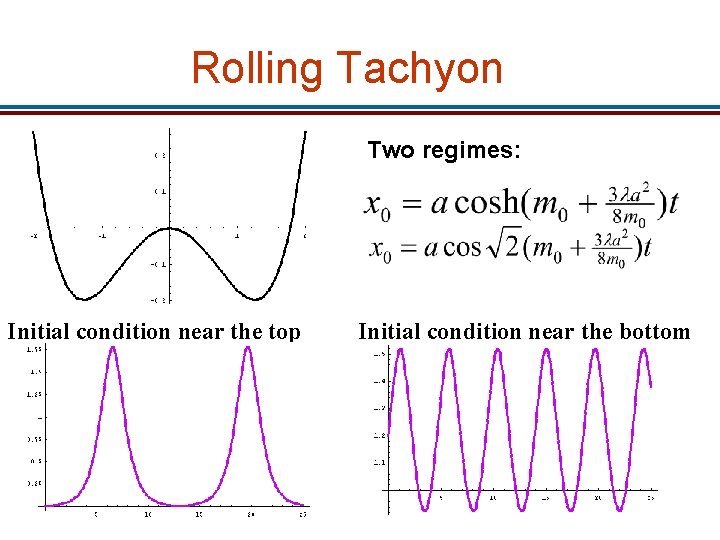
Rolling Tachyon Two regimes: Initial condition near the top Initial condition near the bottom

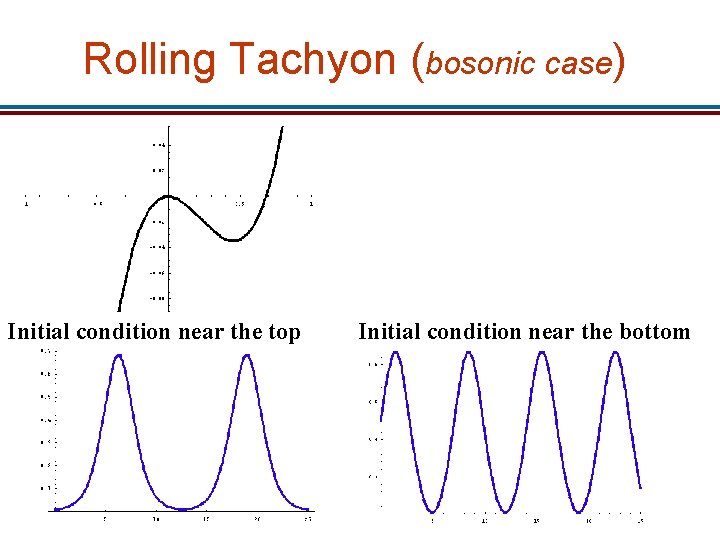
Rolling Tachyon (bosonic case) Initial condition near the top Initial condition near the bottom

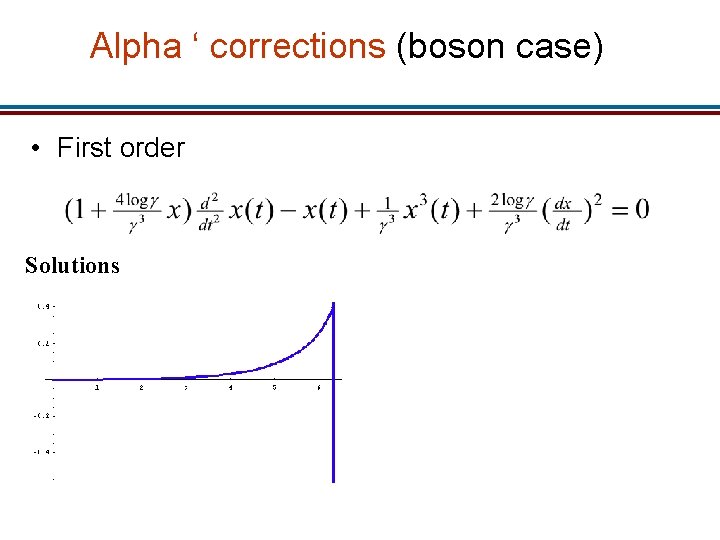
Alpha ‘ corrections (boson case) • First order Solutions

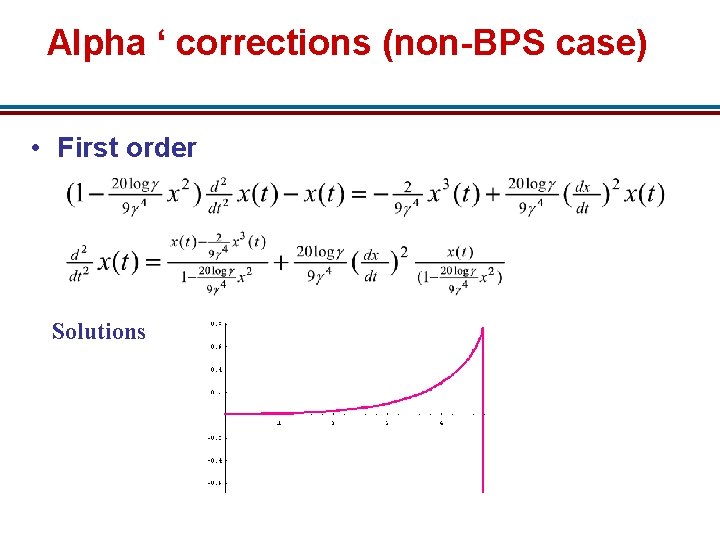
Alpha ‘ corrections (non-BPS case) • First order Solutions

Solutions to SFT E. O. M. Siegel gauge Usual pert. theory = -- + Resonance + … Sen, hepth/020715 Problems!!!

Solutions to SSFT E. O. M. NS sector No picture changing operator Problems!!! defines the fold AMZ, 1990

NO OPEN STRING EXCITATIONS VSFT

Vacuum String Field Theory on a non-BPS brane I. A. , Belov, Giryavets (2002)

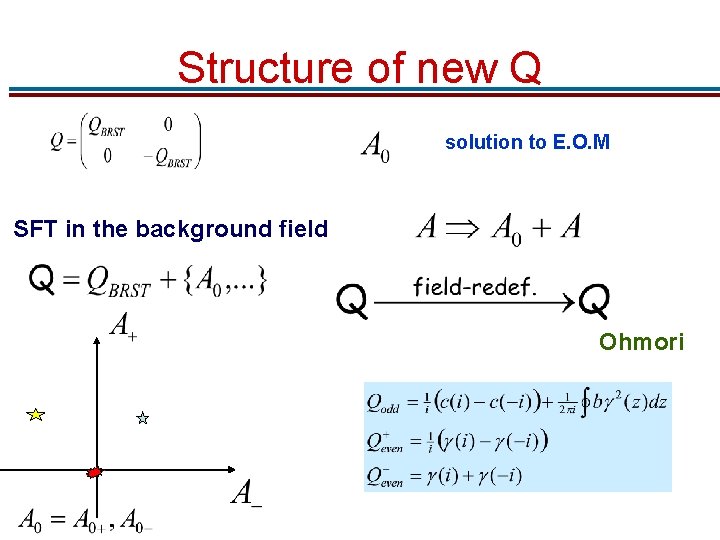
Structure of new Q solution to E. O. M SFT in the background field Ohmori

Tests Solution to VSFT E. O. M

E. O. M. Analog of Noncommutative Soliton in Strong Coupling Limit Gopakumar, Minwalla, Strominger

Methods of solving • Algebraic method • Surface states method • Moyal representation • Half-strings I. Bars, M. Douglas, G. Moore

Algebraic Method Identities for squeezed states Bosonic sliver Rastelli, Sen, Zwiebach; Kostelecky, Potting. . . I. A. , Giryavets, Medvedev; Marino, Schiappa

Twisted Super. Sliver • Superghost twisted sliver equation • Sliver with insertion • Picture changing

Sliver in the Moyal representation Identity Sliver

Conclusion • What we know • What we get • Open problems

What we have got in cubic SSFT Tachyon condensation Rolling tachyon near the top Vacuum SSFT and some solutions

What we know SFT proposes a hard, but a surmountable way to get answers concerning non-perturbative phenomena Two sets of basis: i) related with spectrum of free string ii) related with "strong coupling “ regime (may be suitable for study VSFT)

Open Problems More tests for checking validity of VSSFT Other solutions (lump, kink solutions); especially with time dependence Use the Moyal basis to construct the tachyon condensate and other solutions Classification of projectors in open string field algebra and its physical meaning Closed string excitations in VSSFT