Rolling Friction How to solve for initial velocity

Rolling Friction

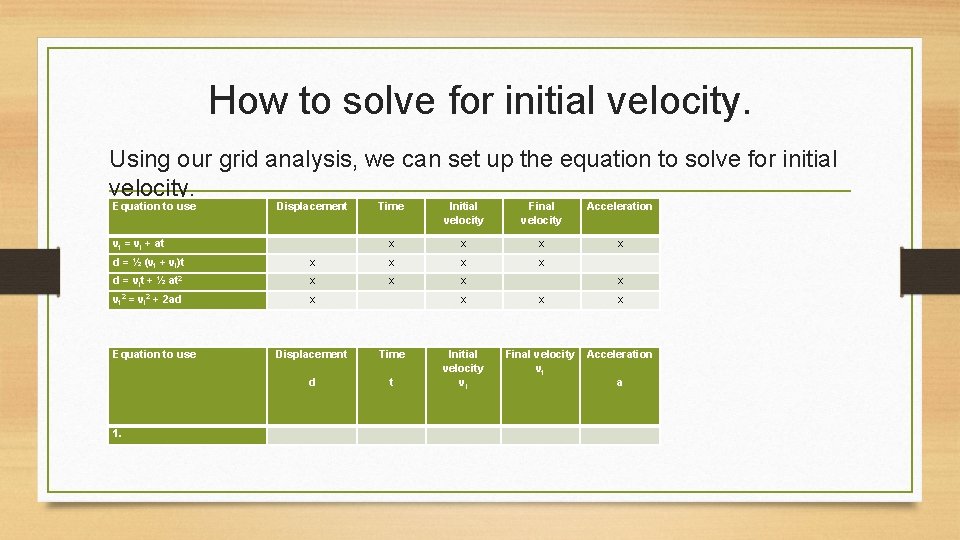
How to solve for initial velocity. Using our grid analysis, we can set up the equation to solve for initial velocity. Equation to use Displacement vf = vi + at Time Initial velocity Final velocity Acceleration x x x d = ½ (vf + vi)t x x x d = vit + ½ at 2 x x x vf 2 x = vi 2 + 2 ad Equation to use 1. Displacement Time d t x x Initial velocity vi Final velocity vf Acceleration a

Solving for initial velocity From our experiment, we measured displacement and time. We let the ball come to a complete stop, so we have the final velocity. Equation to use Displacemen t Time t d 1. x x Initial velocity vi Final velocity vf ? x Acceleratio n a From our list of 4 equations, we should choose the 2 nd equation. d = ½ (vf + vi) t

Solving for initial velocity d = ½ (vf + vi) t Rearrange the equation to solve for vi. Multiple both sides to remove the ½ , we get 2 d = (vf + vi) t Divide both sides by t, we get 2 d/t = vf + vi Subtract both sides by vf, we get 2 d/t – vf = vi Since vf = 0, the final equation is vi = 2 d/t

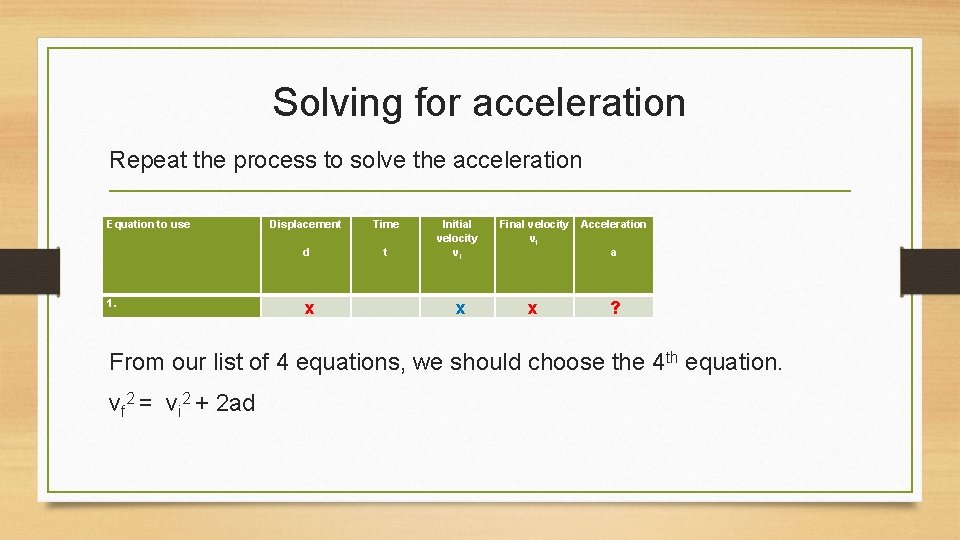
Solving for acceleration Repeat the process to solve the acceleration Equation to use 1. Displacement Time d t x Initial velocity vi Final velocity vf Acceleration x x ? a From our list of 4 equations, we should choose the 4 th equation. vf 2 = vi 2 + 2 ad

Solving for acceleration vf 2 = vi 2 + 2 ad Rearrange the equation to solve for a. Subtract both sides by vi 2, we get vf 2 – vi 2 = 2 ad Divide both sides by 2 d, we get (vf 2 – vi 2 )/2 d = a Since vf = 0, the final equation is vi 2 /2 d = a Knowing that this is “deceleration”, use negativea = - vi 2 /2 d (note: be cautious when entering values into the calculator. Put parenthesis around the 2 d - vi 2 /(2 d) because it is in the denominator)

Alternative to getting acceleration? Can we use another equation to get acceleration without using the initial velocity?

Solving for the coefficient of rolling friction Once we have our acceleration, we can use the equation m = a/g where a is the acceleration of the object and g is the acceleration due to gravity.

Conclusion Final conclusion about the rolling objects. Which characteristics of the object do you think was the most responsible for the largest deceleration (leading to the greatest coefficient of rolling friction) of the object? size, mass, smoothness, etc.

Final thoughts What do you think would happen if instead of carpet, we were using the gym floor. Would the results be the same? Would the properties of the object change the out?