Robust Statistics Why do we use the norms

Robust Statistics Why do we use the norms we do? Henrik Aanæs IMM, DTU haa@imm. dtu. dk A good general reference is: Robust Statistics: Theory and Methods, by Maronna, Martin and Yohai. Wiley Series in Probability and Statistics

How Tall are You ?

Idea of Robust Statistics To fit or describe the bulk of a data set well without being perturbed (influenced to much) by a small portion of outliers. This should be done without a pre-processing segmentation of the data. We thus now model our data set as consisting of inliers, that follow some distribution, at outliers which do not. Inliers Outliers can be interesting too!

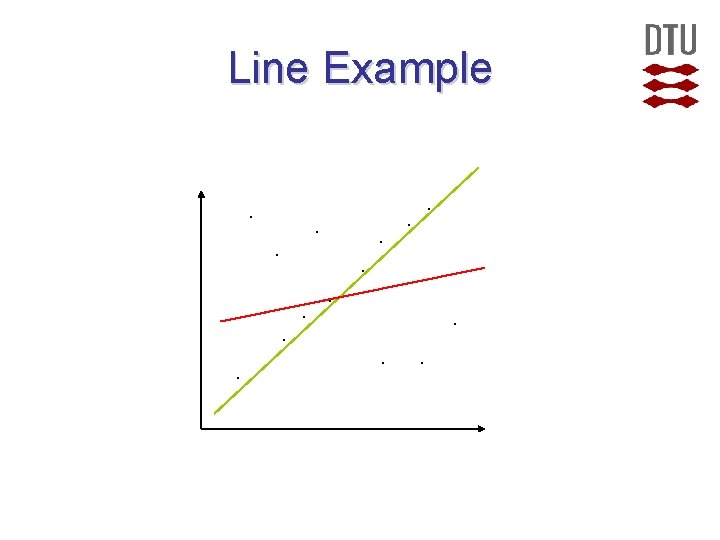
Line Example. . .

Robust Statistics in Computer Vision Image Smoothing Image by Frederico D'Almeida

Robust Statistics in Computer Vision Image Smoothing

Robust Statistics in Computer Vision optical flow Play Sequence MIT BCS Perceptual Science Group. Demo by John Y. A. Wang.

Robust Statistics in Computer Vision tracking via view geometry Image 1 Image 2

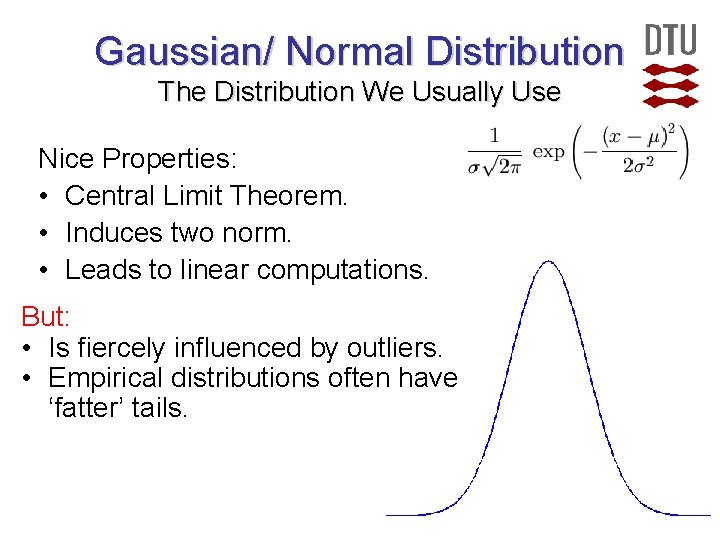
Gaussian/ Normal Distribution The Distribution We Usually Use Nice Properties: • Central Limit Theorem. • Induces two norm. • Leads to linear computations. But: • Is fiercely influenced by outliers. • Empirical distributions often have ‘fatter’ tails.

Gaussians Just are Models Too Alternative title of this talk

Error or ρ-functions Converting from Model-Data Deviation to Objective Function.

ρ-functions and ML A typical way of forming ρ- functions

ρ-functions and ML II A typical way of forming ρ- functions

ρ-functions and ML II A typical way of forming ρ- functions

Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared General Idea: Down weigh outliers, i. e. ρ(x) should be ‘smaller’ for large |x|.

Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared • Induced by Gaussian. • Very non-robust. • ‘Standard’ distribution.

Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared • Quite Robust. • Convex. • Corresponds to Median.

The Median and the 1 -Norm

The Median and the 1 -Norm Example with 2 observations

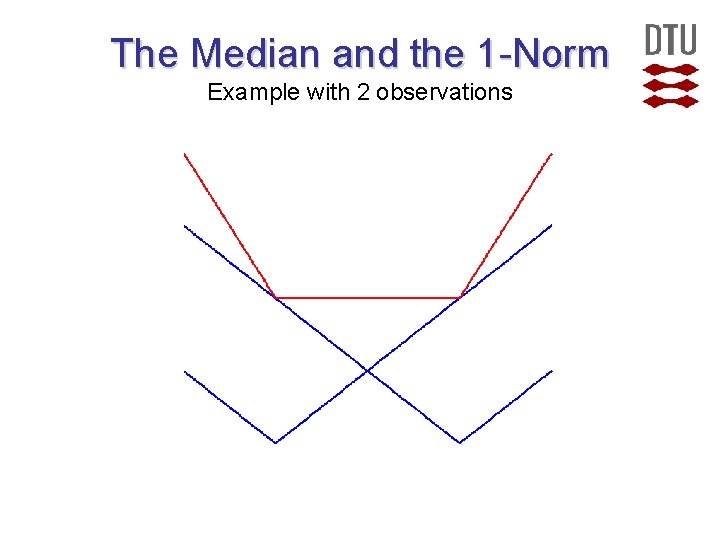
The Median and the 1 -Norm Example with 2 observations

The Median and the 1 -Norm Example with more observations

Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared • Quite Robust. • Convex. • Corresponds to Median.

Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared • Mixture of 1 and two norm. • Convex. • Has nice theoretical properties.

Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared • Discards Outlier’s. • For inliers works as Gaussian. • Has discontinues derivative.

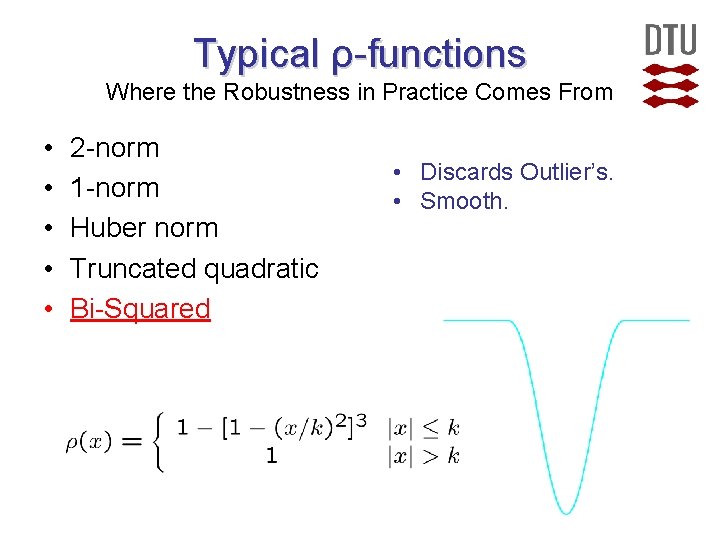
Typical ρ-functions Where the Robustness in Practice Comes From • • • 2 -norm 1 -norm Huber norm Truncated quadratic Bi-Squared • Discards Outlier’s. • Smooth.

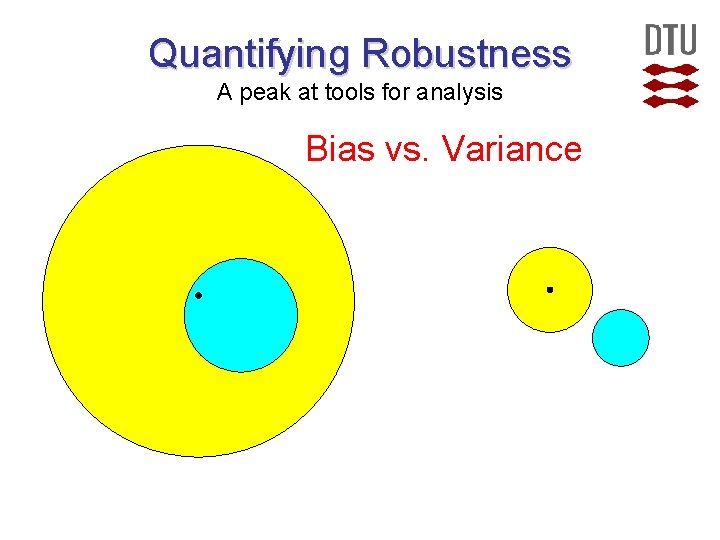
Quantifying Robustness A peak at tools for analysis Bias vs. Variance

Quantifying Robustness A peak at tools for analysis Related to variance, on the previous slide

Quantifying Robustness You want to be robust over a range of models

Quantifying Robustness A peak at tools for analysis Other measures (Similar): • Breakage Point: How many outliers can an estimator handle and still give ‘reasonable’ results. • Asymptotic bias: What bias does an outlier impose.

Back to Images here we have multiple ‘models’ To fit or describe the bulk of a data set well without being perturbed (influenced to much) by a small portion of outliers. This should be done without a pre-processing segmentation of the data.

Optimization Methods Typical Approach: 1. Find initial estimate. 2. Use Non-linear optimization and/or EMalgorithm. NB: In this course we have and will seen other methods e. g. with guaranteed convergence

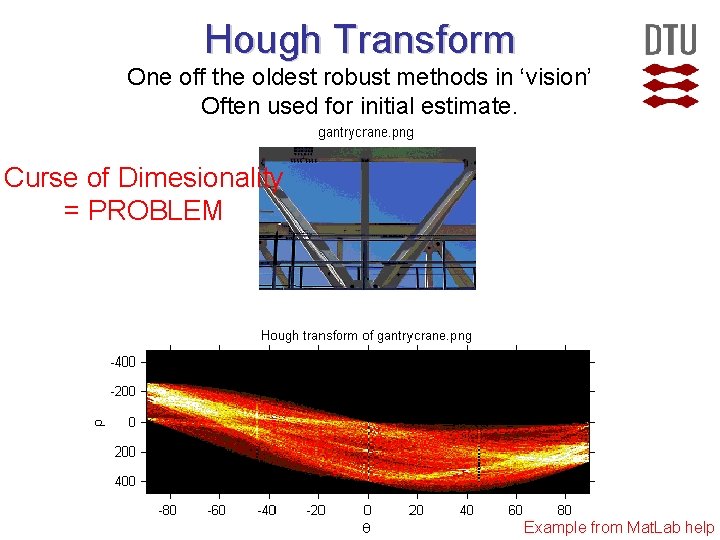
Hough Transform One off the oldest robust methods in ‘vision’ Often used for initial estimate. Curse of Dimesionality = PROBLEM Example from Mat. Lab help

Ran. Sa. C Sampling in Hough space, better for higher dimensions RANdom SAmpling Consensus, RANSAC Iterate: 1. Draw minimal sample. 2. Fit model. 3. Evaluate model by Consensus. In a Hough setting: • 1. and 2. corresponds to finding a ‘good’ bin in Hough space. • 3. Corresponds to calculating the value. Run Ran. Demo. m

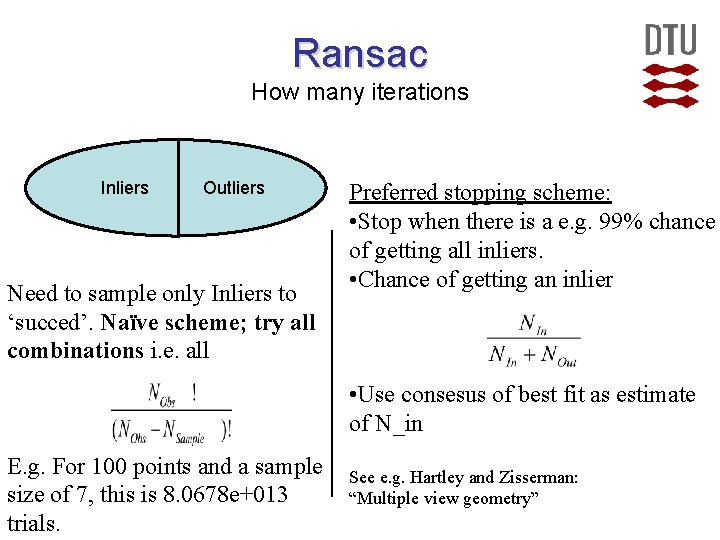
Ransac How many iterations Inliers Outliers Need to sample only Inliers to ‘succed’. Naïve scheme; try all combinations i. e. all Preferred stopping scheme: • Stop when there is a e. g. 99% chance of getting all inliers. • Chance of getting an inlier • Use consesus of best fit as estimate of N_in E. g. For 100 points and a sample size of 7, this is 8. 0678 e+013 trials. See e. g. Hartley and Zisserman: “Multiple view geometry”

Iteratively Reweighted Least Squares IRLS EM-type or chicken and egg optimization