Robust Moving Leastsquares Fitting with Sharp Features Shachar

Robust Moving Least-squares Fitting with Sharp Features Shachar Fleishman, Danieal Cohen-Or and Claudio Silva SIGGRAPH 2005
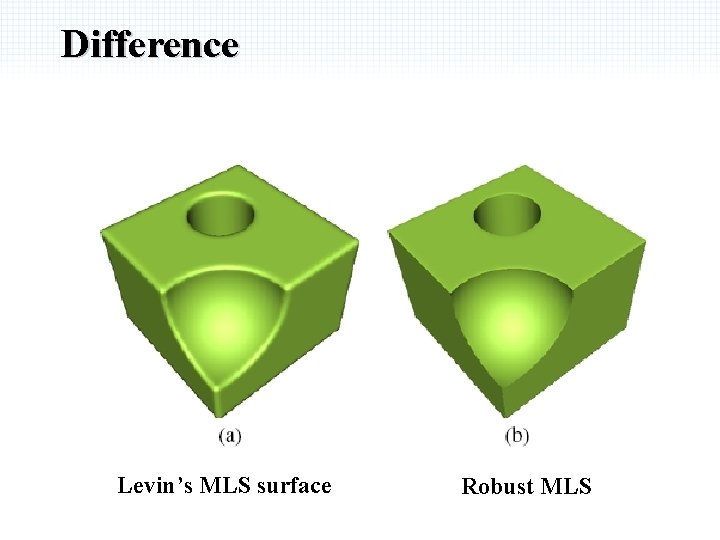
Difference Levin’s MLS surface Robust MLS

Currently Research Trend • Statistical method – Using pattern recognition • MPI – Won-Ki Jeong, Ioannis Ivrissimtzis, Hans-Peter Seidel. “Neural Meshes: Statistical Learning based on Normals, ” In Proc. Pacific Graphics, 2003. – H. Yamauchi, S. Lee, Y. Ohtake, A. Belyaev, and H. P. Seidel, Feature Sensitive Mesh Segmentation with Mean Shift, Shape Modeling International 2005

Abstract • Robust moving least-squares technique for reconstructing a piecewise smooth surface from a noisy point cloud • Use robust statistics method – Forward-search paradigm – Define sharp features

Contributions • Generate the representation from a noisy data set

Background and related work • Surface reconstruction should be insensitive to noise • Generate a piecewise smooth surfaces which adequately represent the sharp features
![Surface Reconstruction • Pioneering work – Hoppe et al. [1994] • Create a piecewise Surface Reconstruction • Pioneering work – Hoppe et al. [1994] • Create a piecewise](http://slidetodoc.com/presentation_image_h/7799428cde37732db671bd790b357de8/image-7.jpg)
Surface Reconstruction • Pioneering work – Hoppe et al. [1994] • Create a piecewise smooth surface in a multiphase process • Sharp features – Two polygons whit a crease angle that is higher than a threshold – Ohtake et al. [2003] • Surface representation – Defined by a blend of locally fitted implicit quadrics – Not sensitive to noise
![Robust statistics methods • Pauly et al. [2004] – Presented a method for measuring Robust statistics methods • Pauly et al. [2004] – Presented a method for measuring](http://slidetodoc.com/presentation_image_h/7799428cde37732db671bd790b357de8/image-8.jpg)
Robust statistics methods • Pauly et al. [2004] – Presented a method for measuring the uncertainty of a point set • Xie et al. [2004] – Extended the MPU technique to handle noisy datasets
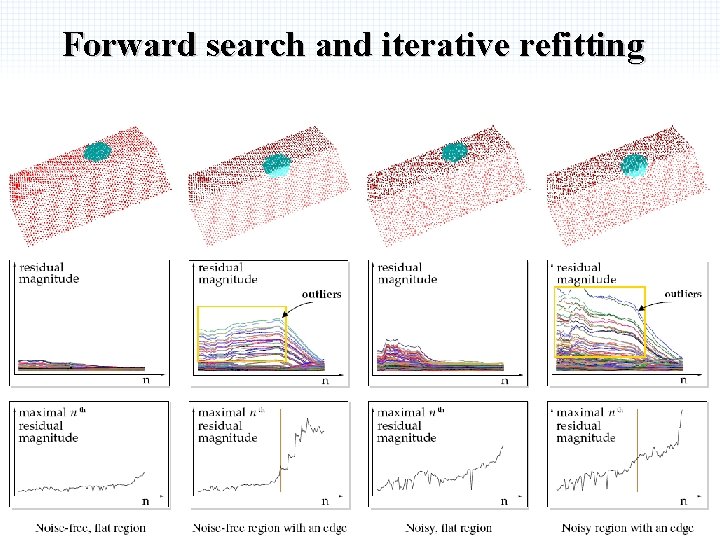
Forward search and iterative refitting

Results • Reconstruction of the fandisk model
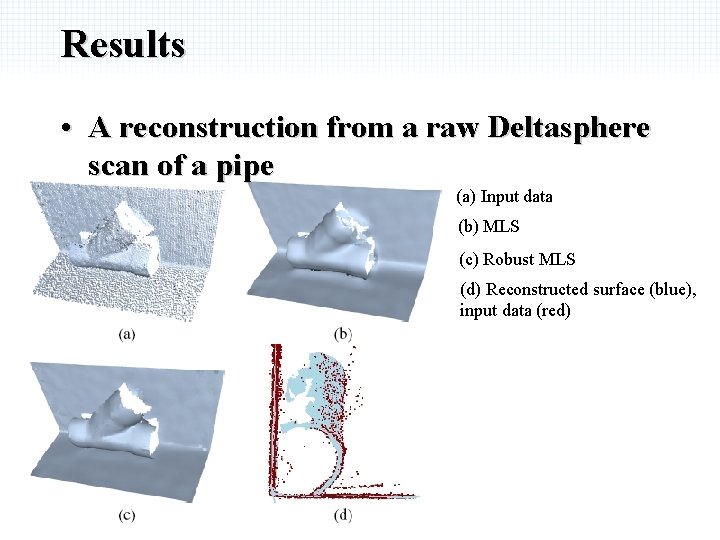
Results • A reconstruction from a raw Deltasphere scan of a pipe (a) Input data (b) MLS (c) Robust MLS (d) Reconstructed surface (blue), input data (red)

Results • Reconstruction of missing data (a) Input data; samples near the edge are missing (b) MLS (c) Robust MLS (d) Points that were projected to the edge are marked in yellow
- Slides: 12