Robust Mobile Robot Navigation Using Visual Landmarks Amy

Robust Mobile Robot Navigation Using Visual Landmarks Amy Briggs Daniel Scharstein Middlebury College Supported in part by NSF grants CCR-9902032, EIA-9806108, by Middlebury College, and by the Howard Hughes Medical Institute.

Student collaborators Darius Braziunas ‘ 00 Cuong Nguyen ‘ 02 Cristian Dima ‘ 99 Sorin Talamba ‘ 01 Huan Ding ‘ 02 Pete Wall ‘ 01

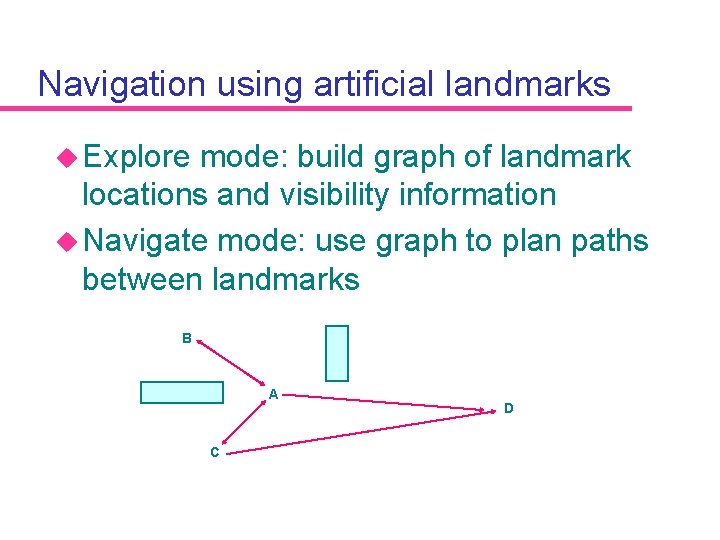
Navigation using artificial landmarks u Explore mode: build graph of landmark locations and visibility information u Navigate mode: use graph to plan paths between landmarks B A C D

Challenges u Deal with uncertainty of recognition and temporary occlusion u Design landmarks to be easily recognized

Related Work • Robot navigation using landmarks u Fennema et al. 1990 u Kavraki & Latombe 1994 u Huttenlocher et al. 1995 u Kosaka & Pan 1995 u Lazanas & Latombe 1995 u Simmons & Koenig 1995 u Nickerson et al. 1998 u Owen & Nehmzow 1998 u Blei & Kaelbling 1999

Related Work • Landmark design u Kabuka & Arenas 1987 u Becker et al. 1995 u Tashiro et al. 1995 u Taylor & Kriegman 1995 u Carlsson et al. 1996 u Lin & Tummala 1997 u Salas et al. 1998

Contributions u Part 1: Robust probabilistic navigation algorithm u Part 2: Landmark design and recognition

Part 1: Robust navigation Key idea Annotate visibility graph with probabilities of landmark detection è Compute expected shortest path

Probabilistic graphs Each edge (i, j) in visibility graph has u Length lij - time to go from i to j u Probability pij - probability that j can be seen from i

Annotating the graph u Length of an edge can be estimated from apparent size of landmark (update estimate when edge is traversed) u Probability of detection is based on history of all observations made at landmark

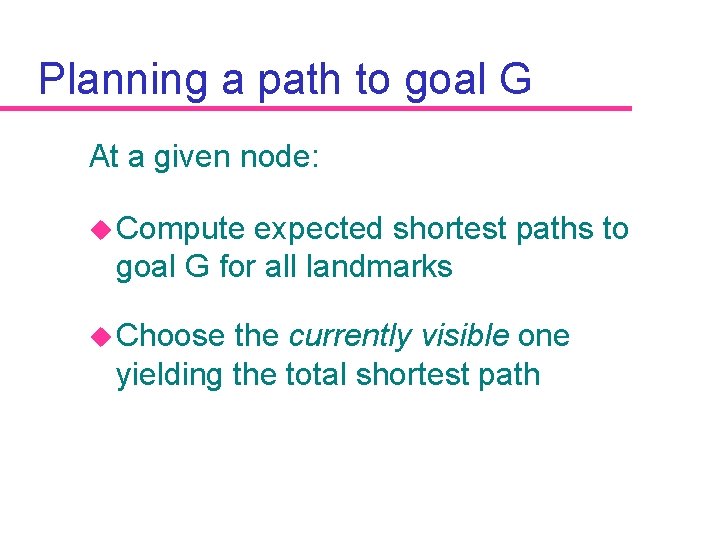
Planning a path to goal G At a given node: u Compute expected shortest paths to goal G for all landmarks u Choose the currently visible one yielding the total shortest path

Planning a path to goal G A G S C

Planning a path to goal G A B G S C

Expected length of shortest path from A to G Let l. AA p. AA = 1. 0 l. AC A p. AB p. AC l. AB B C

Recurrence relations among the u. A node with outdegree d contributes 2 d minima expressions u If ordering among outgoing edges is given, relations reduce to a system of linear equations

Solving for the u Two algorithms: 1. Iterate the equations 2. Repeatedly solve linear system (based on ordering resulting from previous solution)

Relation to MDPs Problem is a special instance of a Markov decision process (MDP) u Each visibility scenario is one state (2 d states per node) u Our algorithms correspond to 1. Value iteration 2. Policy iteration

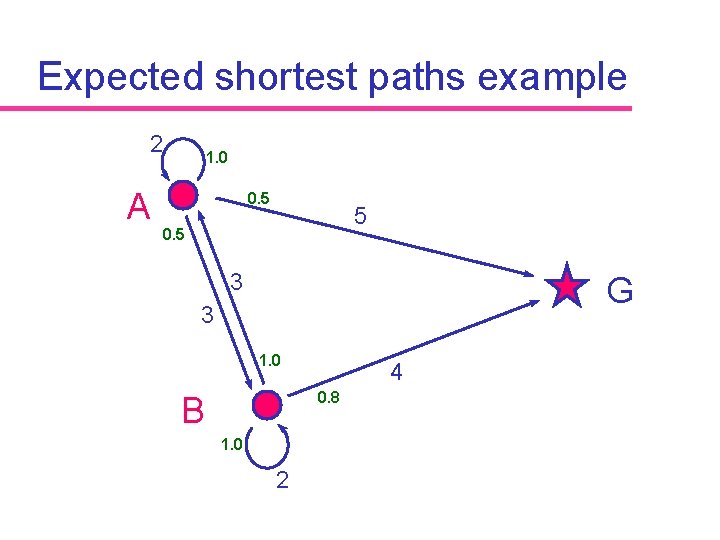
Expected shortest paths example 2 A 1. 0 0. 5 5 0. 5 3 G 3 1. 0 4 0. 8 B 1. 0 2

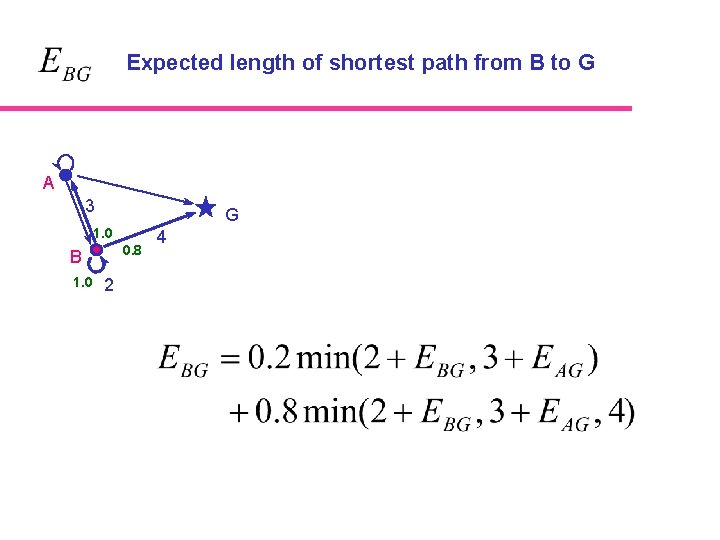
Expected length of shortest path from B to G A 3 G 1. 0 0. 8 B 1. 0 2 4

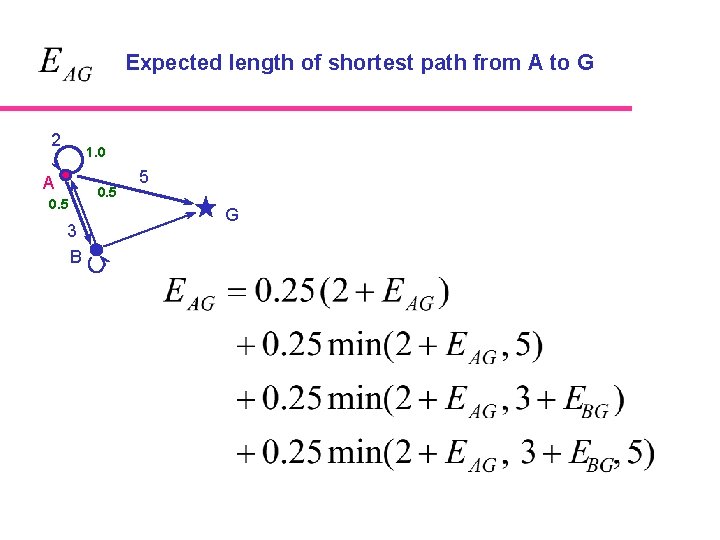
Expected length of shortest path from A to G 2 1. 0 A 0. 5 3 B 0. 5 5 G

Value iteration example k 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 E_AG 0. 00000 2. 00000 4. 00000 5. 50000 6. 22500 6. 42625 6. 48056 6. 49494 6. 49869 6. 49967 6. 49991 6. 49998 6. 49999 6. 50000 E_BG 0. 00000 2. 00000 4. 40000 4. 48000 4. 49600 4. 49920 4. 49984 4. 49997 4. 49999 4. 50000 E_GG 0. 00000 0. 00000

Convergence u Theorem: If there is a path from every node to the goal, the system of equations has a unique solution, and value iteration converges to it. u Rate of convergence is geometric

Contributions 4 Part 1: Robust probabilistic navigation algorithm u Part 2: Landmark design and recognition

Part 2: Landmark design Key idea Use a self-similar pattern (fractal) è Invariant to scale

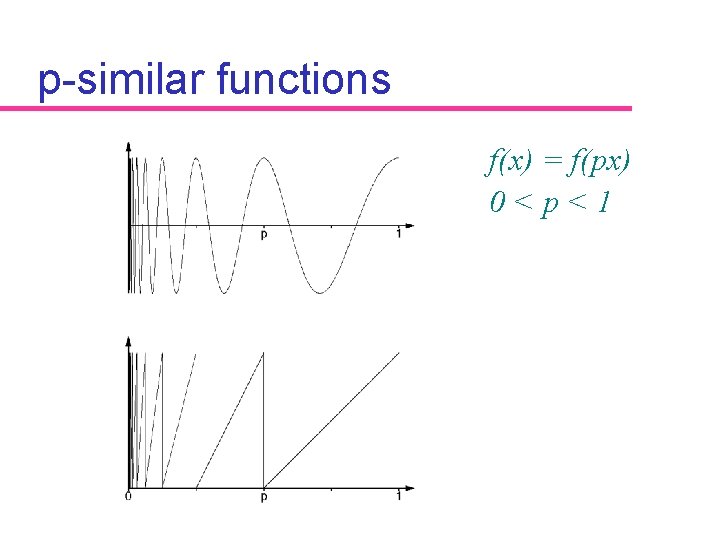
p-similar functions f(x) = f(px) 0<p<1

Detecting p-similar intensities compute average difference between function and scaled function: f p-similar iff

Avoiding false positives Maximize match for scale p Maximize mismatch for scale Öp è e maximiz

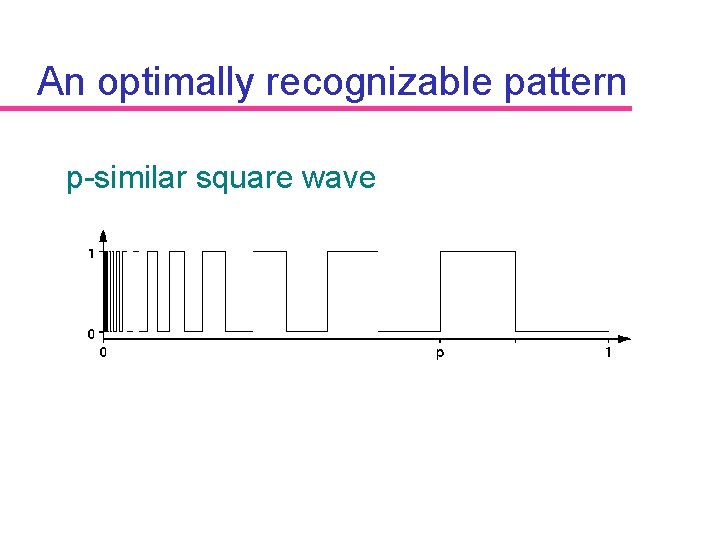
An optimally recognizable pattern p-similar square wave

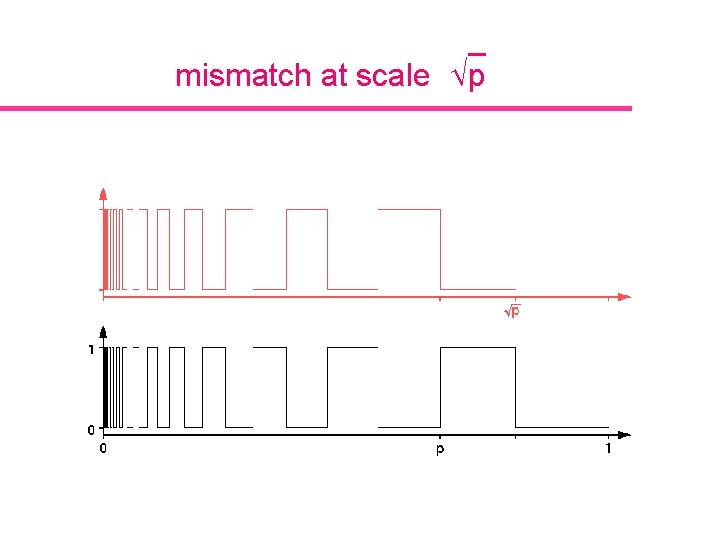
mismatch at scale Öp

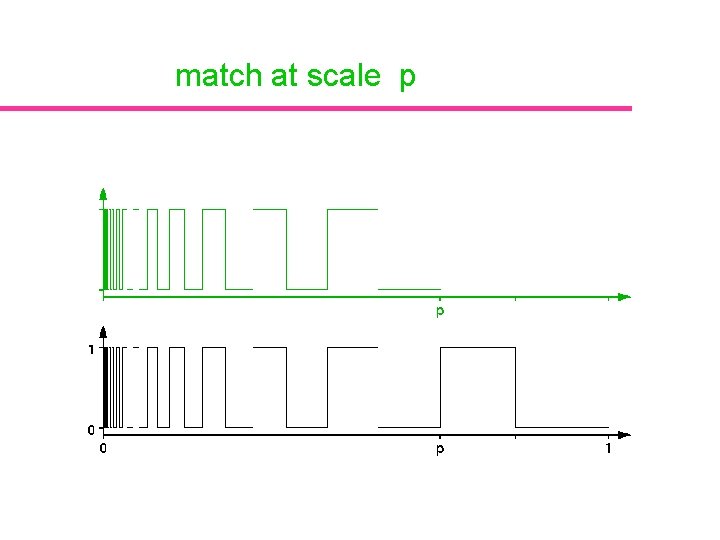
match at scale p

Recognition algorithm For every kth scanline in the image • compute match function m at all pixels • mark strong local maxima as matches è Invariant to affine transformations of the landmark pattern

Pose estimation & barcodes u Fit straight line to each set of consecutive matches u Find top and bottom boundaries of pattern u Decode barcode

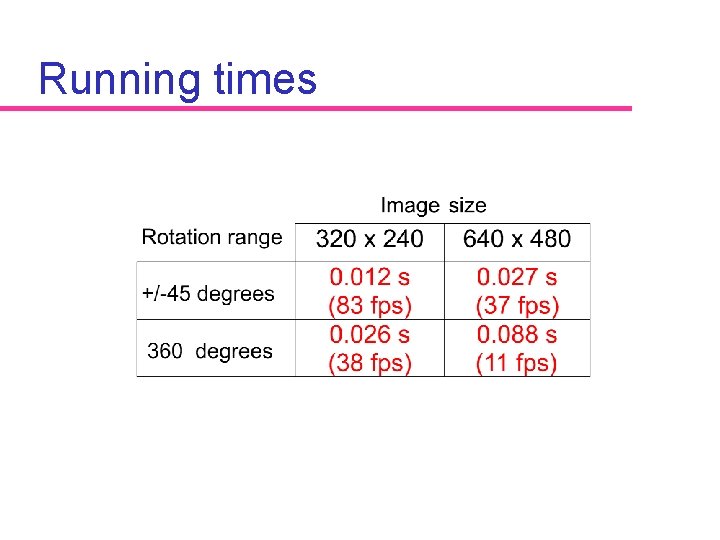
Running times

Conclusion u Robust visibility-graph navigation using expected shortest paths (MDP model) u First real-time recognition method to employ full affine invariants u Landmark code available at http: //www. middlebury. edu/~schar/landmark

Future work Landmarks: u Estimation of perspective transform u Hierarchical barcodes Navigation: u Large-scale experiments