Robust and Universal Reversible Machines HighLevel Programming Languages

Robust and Universal Reversible Machines & High-Level Programming Languages in a Recombinase DNA System A Forthcoming Proposal • Principal Investigators: – Junghuei Chen (Chem. , U. Del. ) – Michael Frank (CISE, U. Fla. ) – Harvey Rubin (Med. , U. Penn. ) – David Wood (CIS, U. Del. )

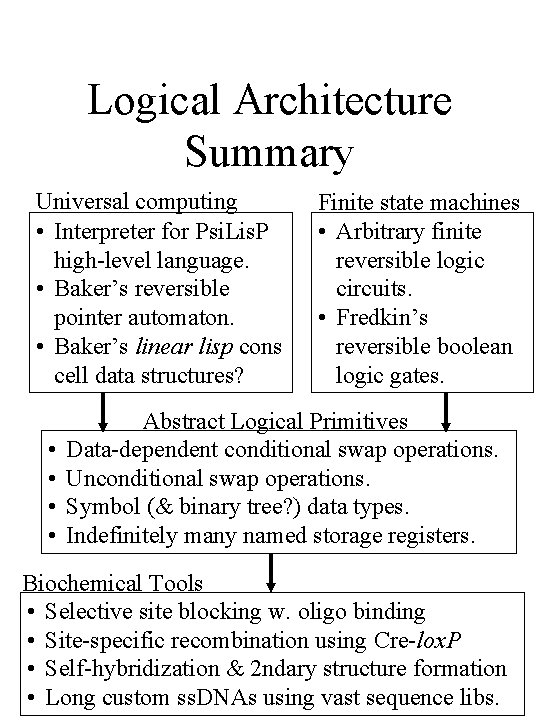
Logical Architecture Summary Universal computing • Interpreter for Psi. Lis. P high-level language. • Baker’s reversible pointer automaton. • Baker’s linear lisp cons cell data structures? • • Finite state machines • Arbitrary finite reversible logic circuits. • Fredkin’s reversible boolean logic gates. Abstract Logical Primitives Data-dependent conditional swap operations. Unconditional swap operations. Symbol (& binary tree? ) data types. Indefinitely many named storage registers. Biochemical Tools • Selective site blocking w. oligo binding • Site-specific recombination using Cre-lox. P • Self-hybridization & 2 ndary structure formation • Long custom ss. DNAs using vast sequence libs.

Biochemical Tools • Large custom sequence library – Funded project, shown yesterday – Goal: Many, distinct oligo sequences, no side reactions • Initial program state: a custom ss. DNA string of “symbols” – Intentional complementary symbols can form ds. DNA in certain selected regions

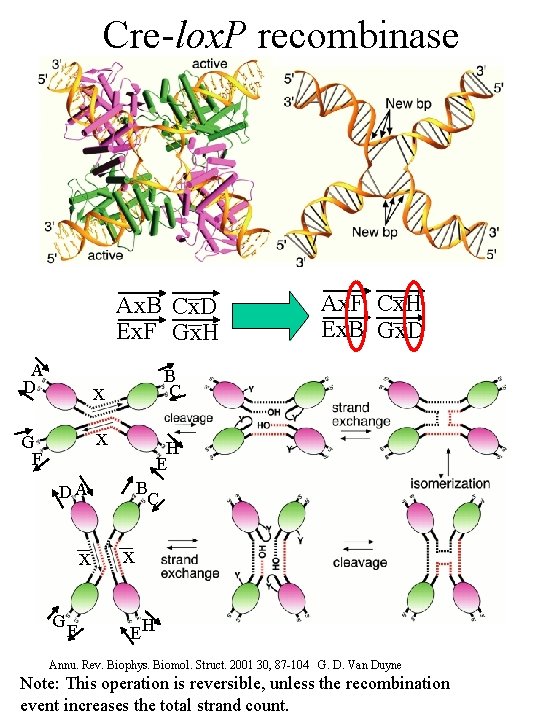
Cre-lox. P recombinase Ax. B Cx. D Ex. F Gx. H A D B C x x G F H E B C DA x G F Ax. F Cx. H Ex. B Gx. D x EH Annu. Rev. Biophys. Biomol. Struct. 2001 30, 87 -104 G. D. Van Duyne Note: This operation is reversible, unless the recombination event increases the total strand count.

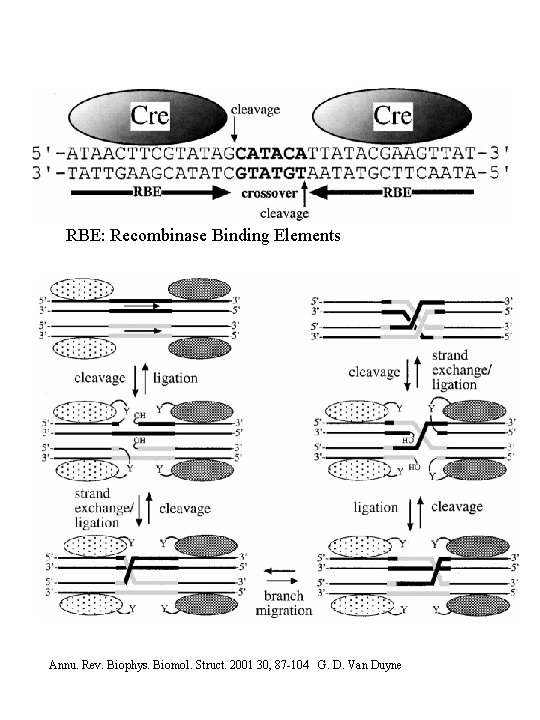
RBE: Recombinase Binding Elements Annu. Rev. Biophys. Biomol. Struct. 2001 30, 87 -104 G. D. Van Duyne

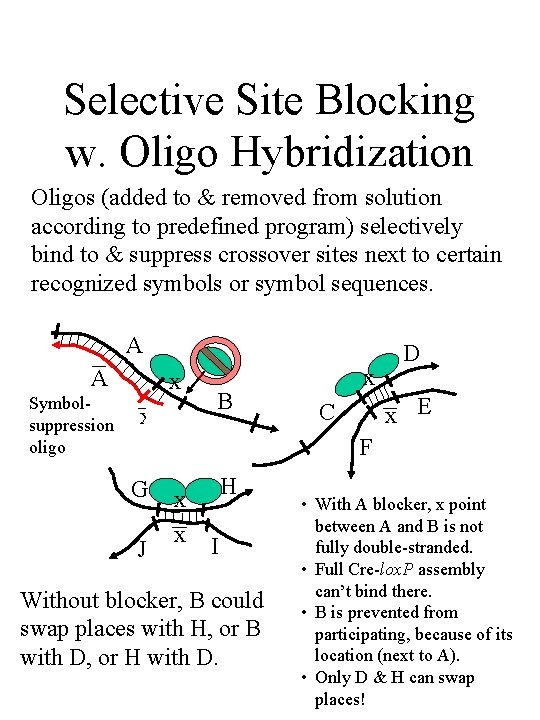
Selective Site Blocking w. Oligo Hybridization Oligos (added to & removed from solution according to predefined program) selectively bind to & suppress crossover sites next to certain recognized symbols or symbol sequences. A A Symbolsuppression oligo x x B x D x E C F G J x x H I Without blocker, B could swap places with H, or B with D, or H with D. • With A blocker, x point between A and B is not fully double-stranded. • Full Cre-lox. P assembly can’t bind there. • B is prevented from participating, because of its location (next to A). • Only D & H can swap places!

Storage Registers • May have indefinitely many registers Ri: R 0, R 1, R 2, … – Addessed by unique labels. – Number limited only by size of symbol-sequence library. • Registers may hold data of any defined type – Atomic symbols: 0, 1, null, etc. – Composite data objects? • Registers accessed via exchange – Suppress the framing labels of all regs but the 2 to be swapped Ri. S x data 1 x Ri. F Ri. S x data 2 x Ri. F Rj. S x data 2 x Rj. F Rj. S x data 1 x Rj. F

Data-Dependent Conditional Swap Operation • Implements: If Ri = c then swap(Ri-1, Ri+1) • Blocker oligo recognizes c in central register & stops swap. R 1 L x data 1 x R 2 L x data 2 x R 3 L x data 3 x R 3 R x R 2 L x c x R 3 L Caveats: (1) Must tune temperature, concentration, label lengths &/or # of base-pair mismatches for blocker oligos so that overall binding probability is sensitive to whether the controlling register 2 data region matches it. (2) Needs extra refinements to irreversibly lock in final state. (Work in progress. )

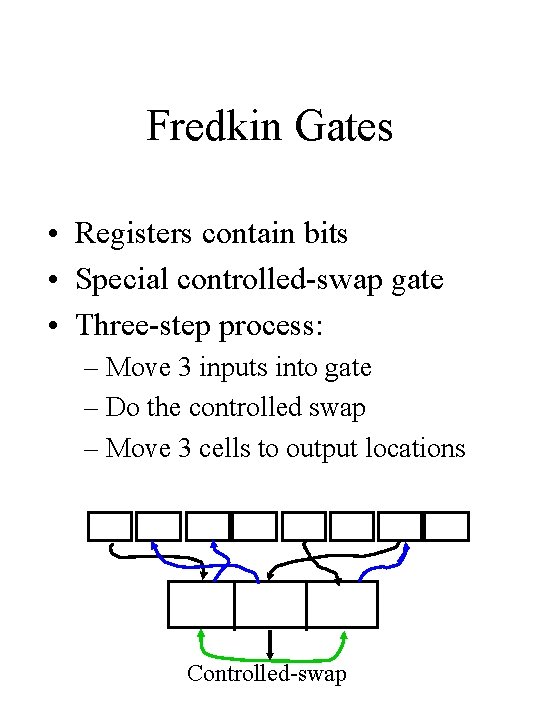
Fredkin Gates • Registers contain bits • Special controlled-swap gate • Three-step process: – Move 3 inputs into gate – Do the controlled swap – Move 3 cells to output locations Controlled-swap

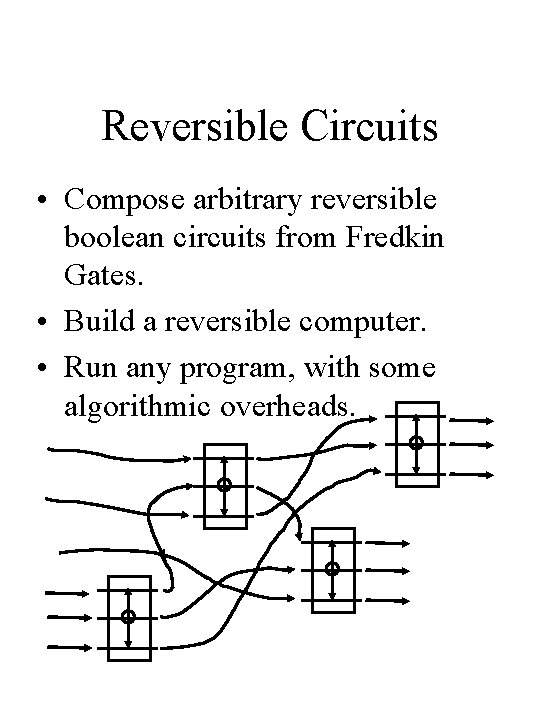
Reversible Circuits • Compose arbitrary reversible boolean circuits from Fredkin Gates. • Build a reversible computer. • Run any program, with some algorithmic overheads.

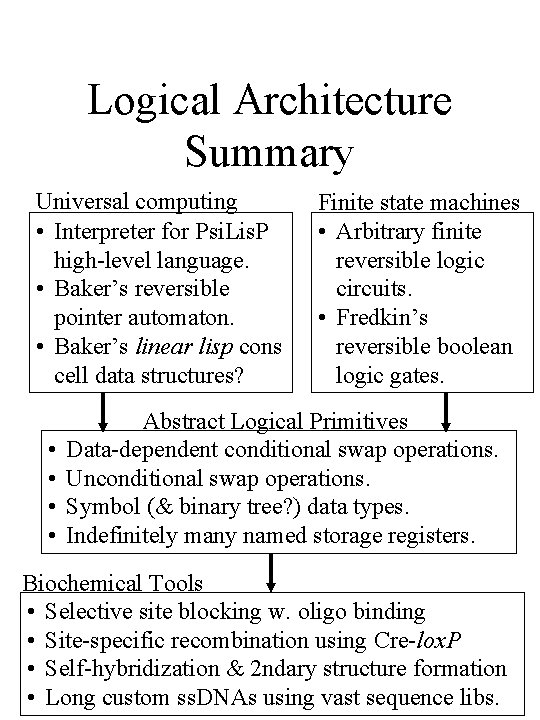
Logical Architecture Summary Universal computing • Interpreter for Psi. Lis. P high-level language. • Baker’s reversible pointer automaton. • Baker’s linear lisp cons cell data structures? • • Finite state machines • Arbitrary finite reversible logic circuits. • Fredkin’s reversible boolean logic gates. Abstract Logical Primitives Data-dependent conditional swap operations. Unconditional swap operations. Symbol (& binary tree? ) data types. Indefinitely many named storage registers. Biochemical Tools • Selective site blocking w. oligo binding • Site-specific recombination using Cre-lox. P • Self-hybridization & 2 ndary structure formation • Long custom ss. DNAs using vast sequence libs.

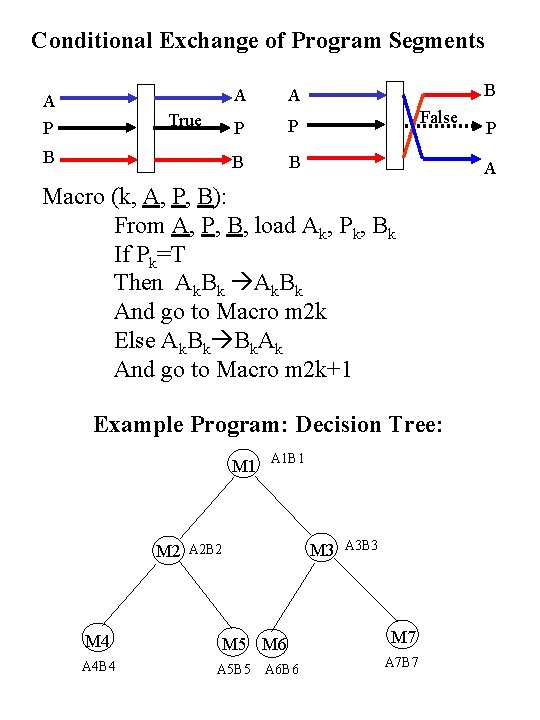
Conditional Exchange of Program Segments A P True B A A P P B B B False A Macro (k, A, P, B): From A, P, B, load Ak, Pk, Bk If Pk=T Then Ak. Bk And go to Macro m 2 k Else Ak. Bk Bk. Ak And go to Macro m 2 k+1 Example Program: Decision Tree: M 1 M 2 M 4 A 4 B 4 A 1 B 1 M 3 A 2 B 2 M 5 M 6 A 5 B 5 A 6 B 6 P A 3 B 3 M 7 A 7 B 7

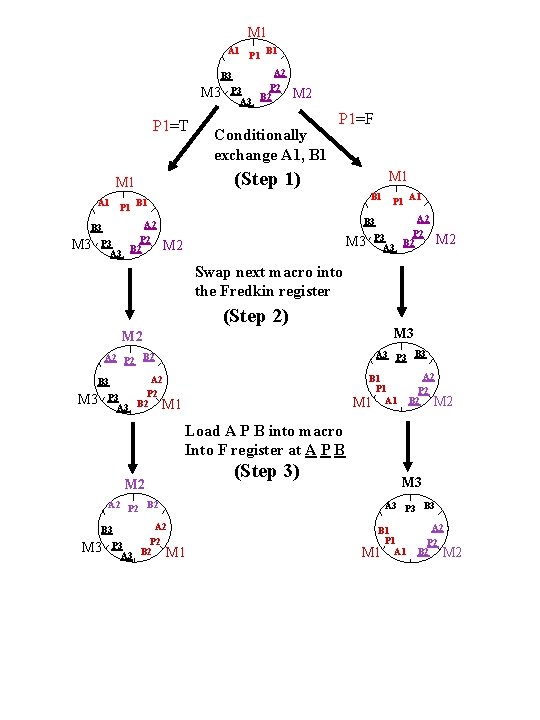
M 1 A 1 P 1 B 1 A 2 P 3 B 2 A 3 B 3 M 3 P 1=T M 2 Conditionally exchange A 1, B 1 P 1=F (Step 1) M 1 B 1 A 1 P 1 B 1 A 2 P 3 A 3 B 2 A 1 A 2 P 3 A 3 B 2 B 3 M 3 P 1 M 3 M 2 Swap next macro into the Fredkin register (Step 2) M 2 M 3 A 2 P 2 B 2 A 3 P 3 B 3 M 3 A 2 P 2 B 2 M 2 B 1 P 1 M 1 A 2 P 3 A 3 B 2 M 1 B 3 Load A P B into macro Into F register at A P B M 2 A 2 P 2 B 2 A 2 P 3 A 3 B 2 M 1 B 3 M 3 (Step 3) M 3 A 3 P 3 B 1 P 1 M 1 A 2 P 2 B 2 M 2

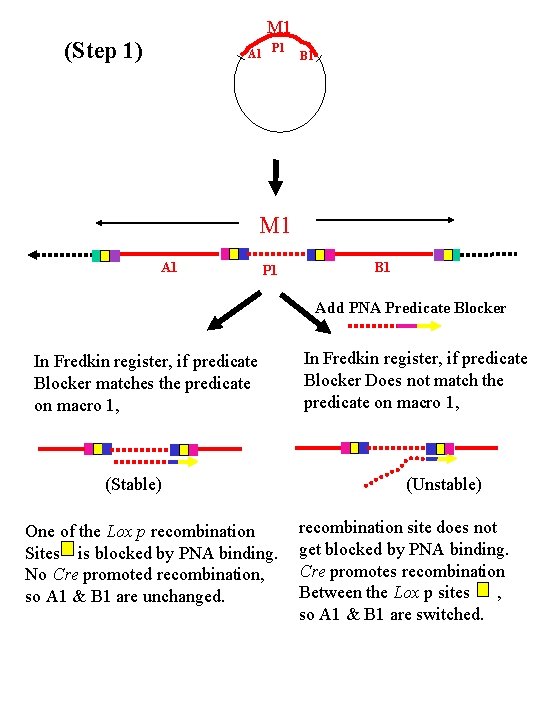
M 1 (Step 1) A 1 P 1 B 1 M 1 A 1 P 1 B 1 Add PNA Predicate Blocker In Fredkin register, if predicate Blocker matches the predicate on macro 1, (Stable) One of the Lox p recombination Sites is blocked by PNA binding. No Cre promoted recombination, so A 1 & B 1 are unchanged. In Fredkin register, if predicate Blocker Does not match the predicate on macro 1, (Unstable) recombination site does not get blocked by PNA binding. Cre promotes recombination Between the Lox p sites , so A 1 & B 1 are switched.

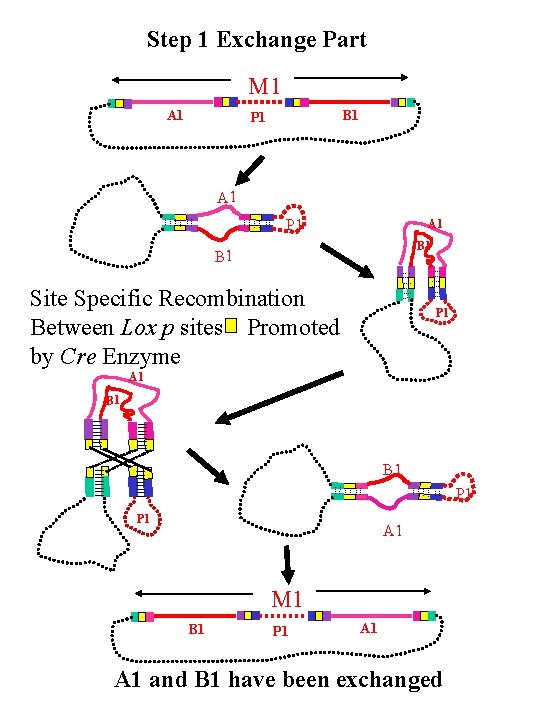
Step 1 Exchange Part M 1 A 1 B 1 P 1 A 1 B 1 Site Specific Recombination Between Lox p sites Promoted by Cre Enzyme P 1 A 1 B 1 P 1 A 1 M 1 B 1 P 1 A 1 and B 1 have been exchanged

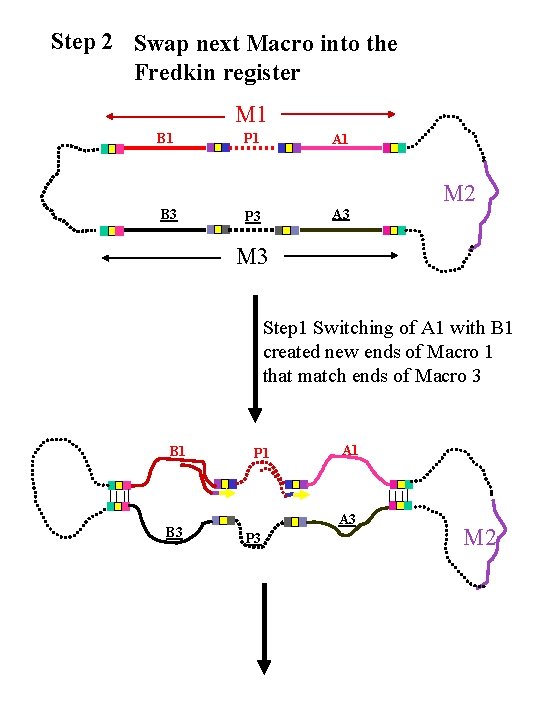
Step 2 Swap next Macro into the Fredkin register M 1 B 1 P 1 A 1 M 2 B 3 A 3 P 3 M 3 Step 1 Switching of A 1 with B 1 created new ends of Macro 1 that match ends of Macro 3 B 1 B 3 P 1 A 3 P 3 M 2

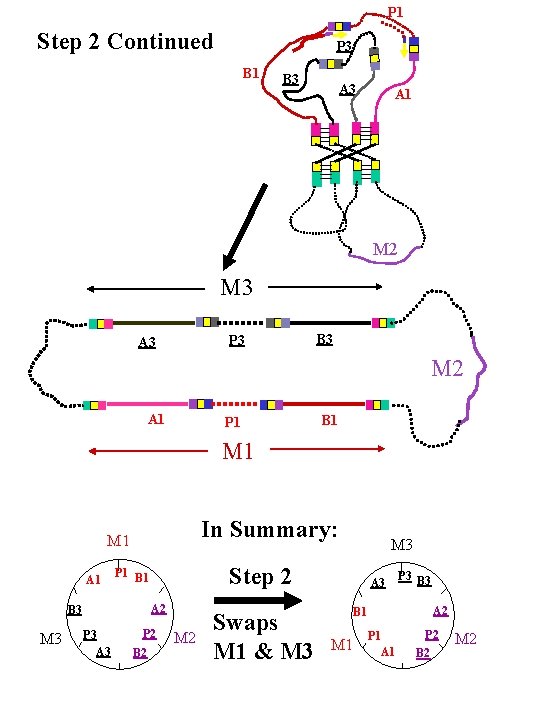
P 1 Step 2 Continued P 3 B 1 B 3 A 1 M 2 M 3 P 3 A 3 B 3 M 2 A 1 P 1 B 1 M 1 In Summary: M 1 A 1 M 3 Step 2 P 1 B 1 A 2 B 3 P 3 A 3 P 2 B 2 M 3 M 2 Swaps M 1 & M 3 A 3 P 3 B 3 A 2 B 1 M 1 P 1 A 1 P 2 B 2 M 2

Binary Tree Data Type • f Ri. L x ( x a x, x b x ) x, x c x ) x Ri. R