Robot Localization Using Bayesian Methods Stochastic Processes Mini

Robot Localization Using Bayesian Methods Stochastic Processes Mini Conference Winter 2011 EE 670 - Prof. Brian Mazzeo Amin Nazaran Stephen Quebe 1

Presentation Outline �Robot Localization �Modeling Robot Localization as a Stochastic Process. �Bayesian Estimation and Filtering. �The Extended Kalman Filter. �Extended Kalman Filter Simulation Results. �Conclusions. 2

Robot Localization �In order for a mobile robot to complete many meaningful tasks, it must be able to identify and control its position in an environment. �“Using sensory information to locate the robot in its environment is the most fundamental problem in robotics [1]. ” 3

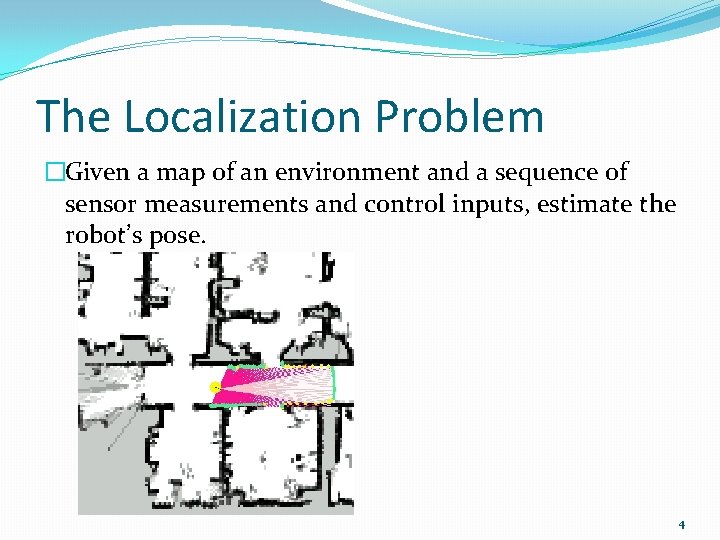
The Localization Problem �Given a map of an environment and a sequence of sensor measurements and control inputs, estimate the robot’s pose. 4

The Localization Problem Inputs Outputs �Robot initial pose. �Estimated robot pose. �Control inputs. �Observations. �Map feature or landmarks. 5

Robot Motion and Observation Models 6

Modeling Robot Localization as a Stochastic Process �One approach to solving this problem is by modeling the robot’s control inputs, observations using a Markov Chain. 7

The Markov Assumption �The Markov assumption states that if we know the current state of the robot, past and future states are conditionally independent of one another. �In other words. If we know where the robot is now, then knowing where the robot was 5 minutes ago doesn’t give us any more information than we already have, regarding it’s current state. �The arrows on Dynamic Bayes Network show this conditional independence. 8

Stochastic Motion Model �The robot motion model describes the robot’s pose as a function of it’s previous pose and control inputs. �The observation model describes the robot’s sensor measurements as a function of the robot’s position and the landmark position. 9

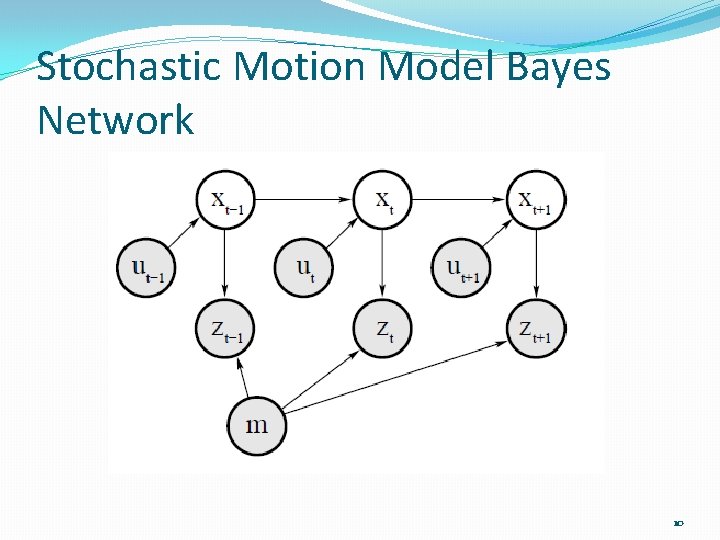
Stochastic Motion Model Bayes Network 10

Bayesian Estimation and Filtering �It is a recursive algorithm. At time t, given the belief at time t-1 belt-1(xr), the last motion control ut-1 and the last measurement zt, determine the new belief belt(xr) as follows: Motion model Measurement model 11

Bayesian Estimation: Prediction Robot pose space Motion model Based on the total probability theorem: (discrete case) where Bi, i=1, 2, . . . is a partition of W. In the continuous case: 12

The Extended Kalman Filter (EKF) �The Extended Kalman Filter is one way to apply Bayesian estimation techniques to robot localization and mapping. �The Kalman filter is the optimal Least Mean Squares estimator of a linear Gaussian system. �The Extended Kalman filter is a way of using the Kalman filter with non-linear models by approximating the model. 13

EKF Assumptions and Violations �Assumptions: �Gaussian noise and uncertainty. �Linear approximations are good. �Markov assumption or complete state assumption holds. �Violations: �Data association create Non-Gaussian uncertainties. �With large time steps or angles the linear approximation is poor. �If the estimate becomes unstable or overconfident the Markov assumption is violated by a poor estimate. �If the robot is “bumped” or moved by something not in the model, the Markov is also violated. 14

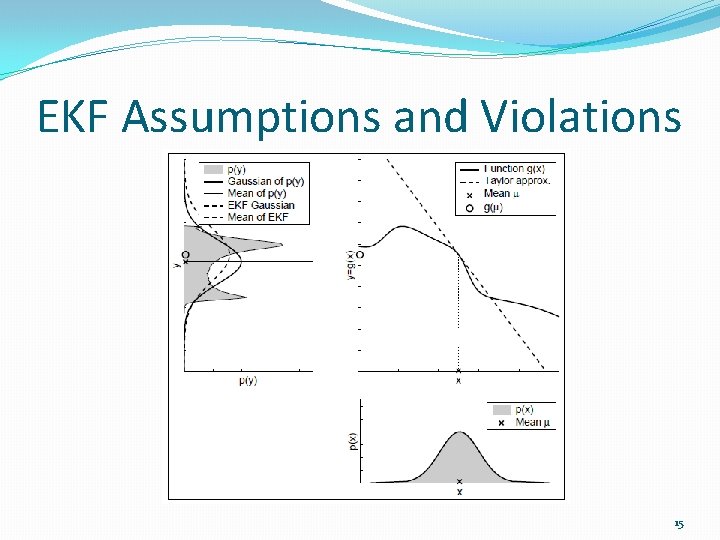
EKF Assumptions and Violations 15

EKF Algorithm 1. EKF_localization ( mt-1, St-1, ut, zt, m): Prediction: 2. Jacobian of g w. r. t location 3. Jacobian of g w. r. t control

EKF Algorithm Continued Motion noise 17 Predicted mean Predicted covariance 17 17

EKF Measurement Update Normalizing factor Measurement model Based on the Bayes Rule: i. e. also: Taking: We have: 18

1. EKF_localization ( mt-1, St-1, ut, zt, m): Correction: 2. 3. Predicted measurement mean Jacobian of h w. r. t location 4. 5. Pred. measurement covariance 6. Kalman gain 7. Updated mean 8. Updated covariance 19

EKF Simulation Results �Normal operation. �Overconfident prediction. �Overconfident measurement. �Large time steps where linearization fails. �External bump where Markov assumption fails. 20

Simulation Results �Show simulation results in real time by opening matlab. 21

Conclusions �The critical assumption in the stochastic model is the Markov assumption. This assumption is restrictive but probably cannot be avoided in any real world scenario. �The Extended Kalman Filter implementation is fast and remains consistent under normal conditions. �In the real world the model can be adjusted to reduce and recover from failure. �The robot must be able to recognize and recover from inevitable failure (the lost robot problem). 22

Thank You For Your Attention Questions? 23

References [1]: I. J. Cox. Blanche—an experiment in guidance and navigation of an autonomous robot vehicle. IEEE Transactions on Robotics and Automation, vol. 7, NO. 2 , pp. 193 – 204, 1991. [2] S. Thrun, W. Burgard, and D. Fox, “Probabilistic Robotics”, MIT press: Cambridge, 1967. 24