Robot Lab Robot Path Planning William Regli Department

Robot Lab: Robot Path Planning William Regli Department of Computer Science (and Departments of ECE and MEM) Drexel University Slide 1

Introduction to Motion Planning • Applications • Overview of the Problem • Basics – Planning for Point Robot – – Visibility Graphs Roadmap Cell Decomposition Potential Field

Goals • Compute motion strategies, e. g. , – Geometric paths – Time-parameterized trajectories – Sequence of sensor-based motion commands • Achieve high-level goals, e. g. , – Go to the door and do not collide with obstacles – Assemble/disassemble the engine – Build a map of the hallway – Find and track the target (an intruder, a missing pet, etc. ) Slide 3
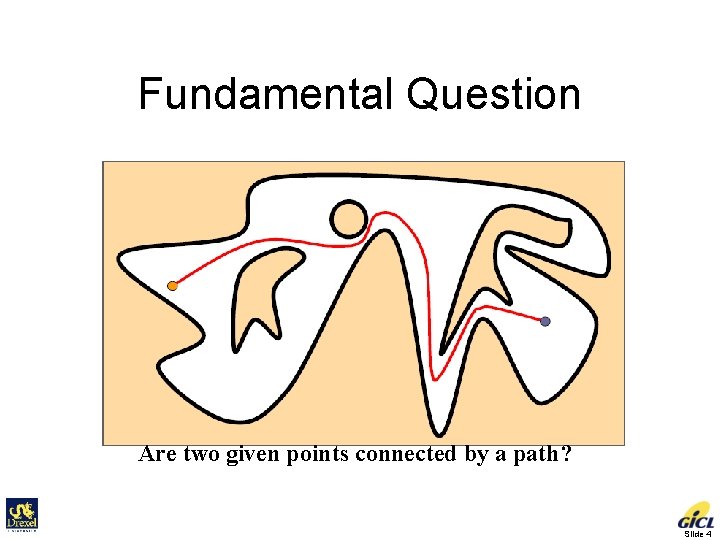
Fundamental Question Are two given points connected by a path? Slide 4

Basic Problem • Problem statement: Compute a collision-free path for a rigid or articulated moving object among static obstacles. • Input – Geometry of a moving object (a robot, a digital actor, or a molecule) and obstacles – How does the robot move? – Kinematics of the robot (degrees of freedom) – Initial and goal robot configurations (positions & orientations) • Output Continuous sequence of collision-free robot configurations connecting the initial and goal configurations Slide 5
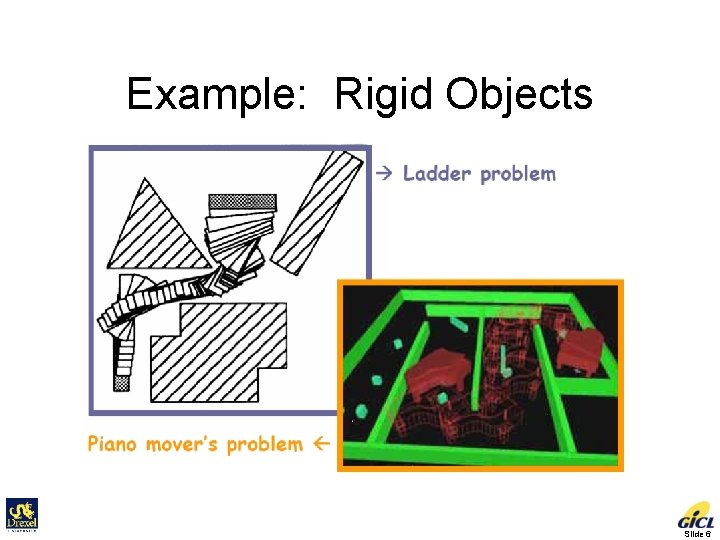
Example: Rigid Objects Slide 6
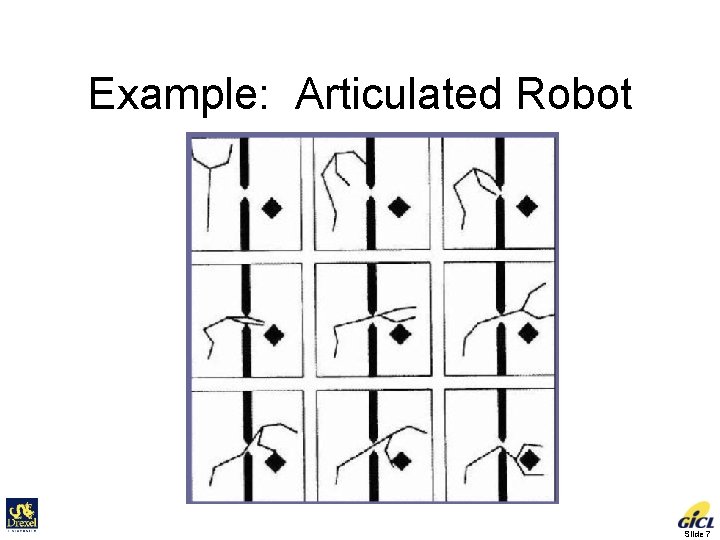
Example: Articulated Robot Slide 7

Is it easy? Slide 8

Hardness Results • Several variants of the path planning problem have been proven to be PSPACE-hard. • A complete algorithm may take exponential time. – A complete algorithm finds a path if one exists and reports no path exists otherwise. • Examples – Planar linkages [Hopcroft et al. , 1984] – Multiple rectangles [Hopcroft et al. , 1984] Slide 9
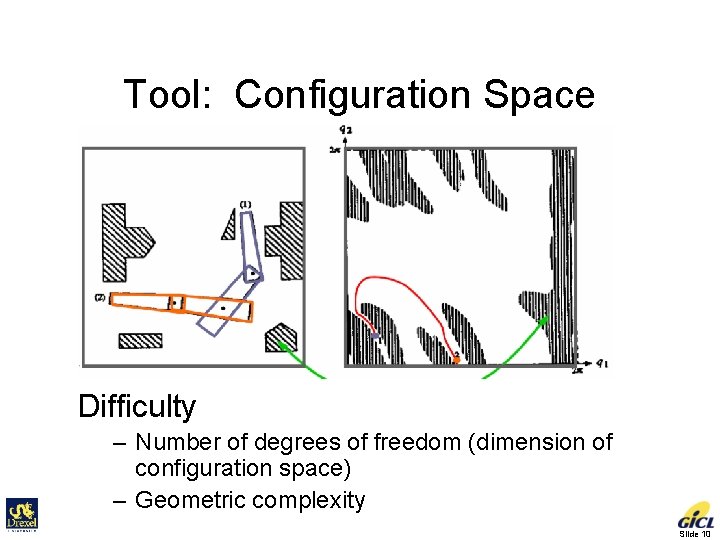
Tool: Configuration Space Difficulty – Number of degrees of freedom (dimension of configuration space) – Geometric complexity Slide 10

Extensions of the Basic Problem • More complex robots – – – Multiple robots Movable objects Nonholonomic & dynamic constraints Physical models and deformable objects Sensorless motions (exploiting task mechanics) – Uncertainty in control Slide 11

Extensions of the Basic Problem • More complex environments – Moving obstacles – Uncertainty in sensing • More complex objectives – – Optimal motion planning Integration of planning and control Assembly planning Sensing the environment • Model building • Target finding, tracking Slide 12

Practical Algorithms • A complete motion planner always returns a solution when one exists and indicates that no such solution exists otherwise. • Most motion planning problems are hard, meaning that complete planners take exponential time in the number of degrees of freedom, moving objects, etc. Slide 13

Practical Algorithms • Theoretical algorithms strive for completeness and low worst-case complexity – Difficult to implement – Not robust • Heuristic algorithms strive for efficiency in commonly encountered situations. – No performance guarantee • Practical algorithms with performance guarantees – Weaker forms of completeness – Simplifying assumptions on the space: “exponential time” algorithms that work in practice Slide 14

• Problem Formulation for Point Robot Input – Robot represented as a point in the plane – Obstacles represented as polygons – Initial and goal positions • Output – A collision-free path between the initial and goal positions Slide 15

Framework Slide 16
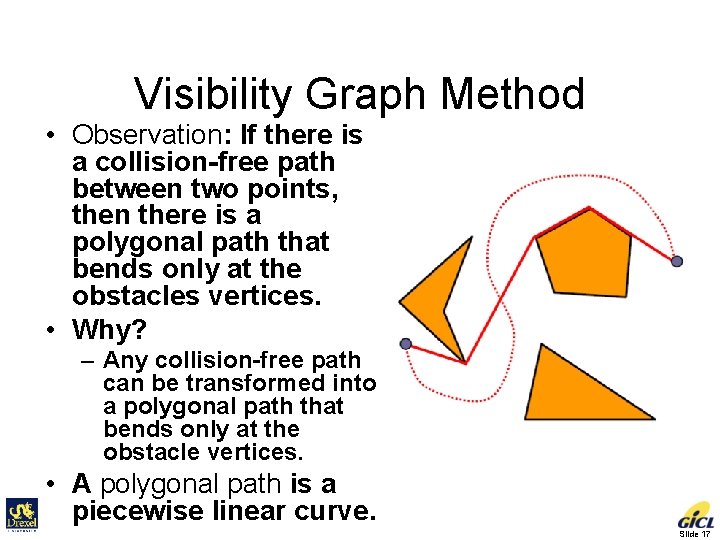
Visibility Graph Method • Observation: If there is a collision-free path between two points, then there is a polygonal path that bends only at the obstacles vertices. • Why? – Any collision-free path can be transformed into a polygonal path that bends only at the obstacle vertices. • A polygonal path is a piecewise linear curve. Slide 17
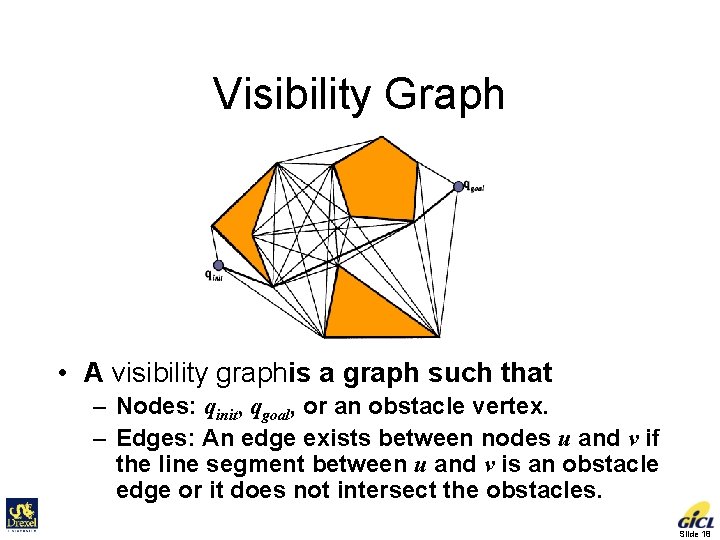
Visibility Graph • A visibility graphis a graph such that – Nodes: qinit, qgoal, or an obstacle vertex. – Edges: An edge exists between nodes u and v if the line segment between u and v is an obstacle edge or it does not intersect the obstacles. Slide 18

A Simple Algorithm for Building Visibility Graphs Slide 19

Computational Efficiency • Simple algorithm O(n 3) time • More efficient algorithms – Rotational sweep O(n 2 log n) time – Optimal algorithm O(n 2) time – Output sensitive algorithms • O(n 2) space Slide 20

Framework Slide 21

Breadth-First Search Slide 22
Breadth-First Search Slide 23
Breadth-First Search Slide 24
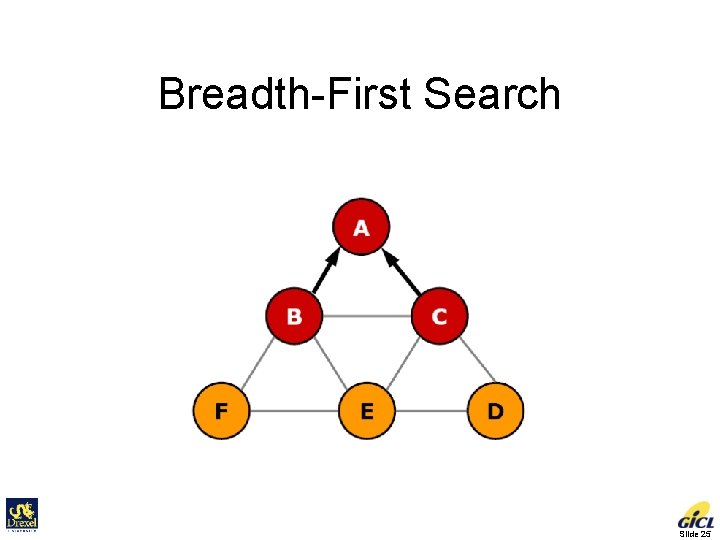
Breadth-First Search Slide 25
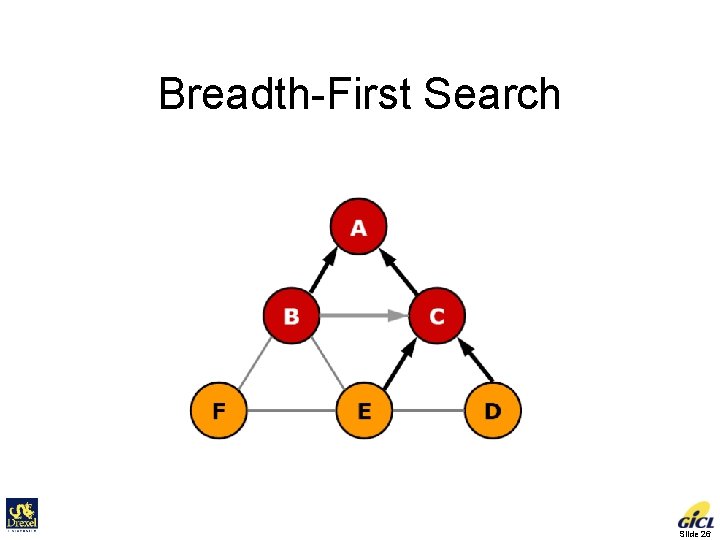
Breadth-First Search Slide 26
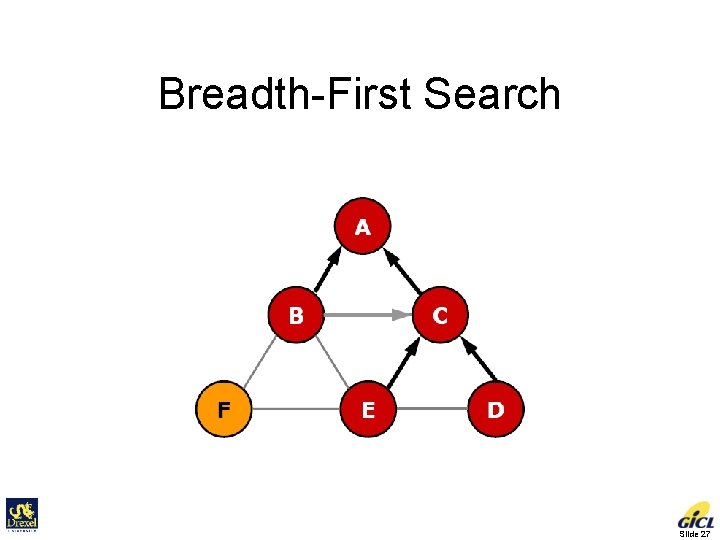
Breadth-First Search Slide 27
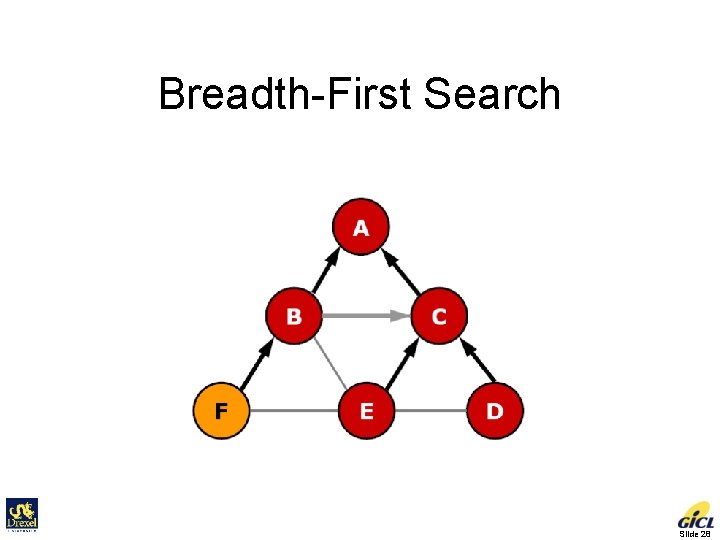
Breadth-First Search Slide 28
Breadth-First Search Slide 29
Breadth-First Search Slide 30

Breadth-First Search Slide 31

Other Search Algorithms • Depth-First Search • Best-First Search, A* Slide 32

Framework Slide 33

Summary • Discretize the space by constructing visibility graph • Search the visibility graph with breadth-first search Q: How to perform the intersection test? Slide 34

Summary • Represent the connectivity of the configuration space in the visibility graph • Running time O(n 3) – Compute the visibility graph – Search the graph – An optimal O(n 2) time algorithm exists. • Space O(n 2) Can we do better? Slide 35

• Classic Path Planning Approaches Roadmap – Represent the connectivity of the free space by a network of 1 -D curves • Cell decomposition – Decompose the free space into simple cells and represent the connectivity of the free space by the adjacency graph of these cells • Potential field – Define a potential function over the free space that has a global minimum at the goal and follow the steepest descent of the potential function Slide 36

Classic Path Planning Approaches • Roadmap – Represent the connectivity of the free space by a network of 1 -D curves • Cell decomposition – Decompose the free space into simple cells and represent the connectivity of the free space by the adjacency graph of these cells • Potential field – Define a potential function over the free space that has a global minimum at the goal and follow the steepest descent of the potential function Slide 37
![Roadmap • Visibility graph Shakey Project, SRI [Nilsson, 1969] • Voronoi Diagram Introduced by Roadmap • Visibility graph Shakey Project, SRI [Nilsson, 1969] • Voronoi Diagram Introduced by](http://slidetodoc.com/presentation_image_h/1f466c3038b2f3ccdc8693758becd507/image-38.jpg)
Roadmap • Visibility graph Shakey Project, SRI [Nilsson, 1969] • Voronoi Diagram Introduced by computational geometry researchers. Generate paths that maximizes clearance. Applicable mostly to 2 -D configuration spaces. Slide 38
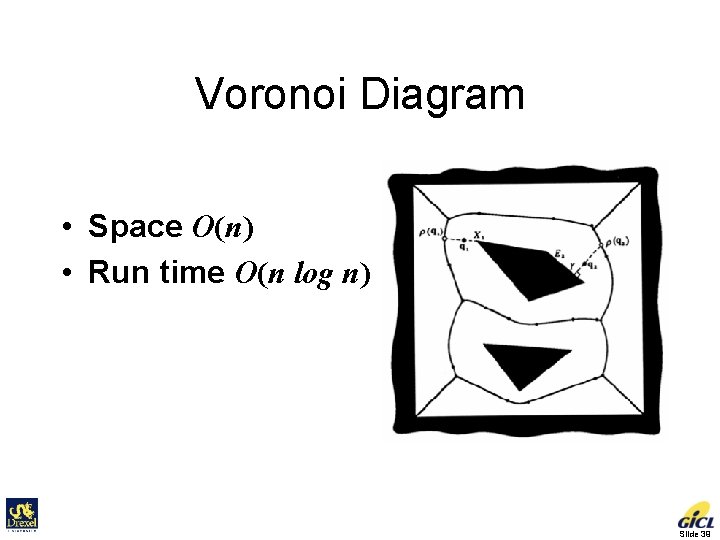
Voronoi Diagram • Space O(n) • Run time O(n log n) Slide 39

Other Roadmap Methods • Silhouette First complete general method that applies to spaces of any dimensions and is singly exponential in the number of dimensions [Canny 1987] • Probabilistic roadmaps Slide 40

• Classic Path Planning Approaches Roadmap – Represent the connectivity of the free space by a network of 1 -D curves • Cell decomposition – Decompose the free space into simple cells and represent the connectivity of the free space by the adjacency graph of these cells • Potential field – Define a potential function over the free space that has a global minimum at the goal and follow the steepest descent of the potential function Slide 41

Cell-decomposition Methods • Exact cell decomposition The free space F is represented by a collection of non-overlapping simple cells whose union is exactly F • Examples of cells: trapezoids, triangles Slide 42
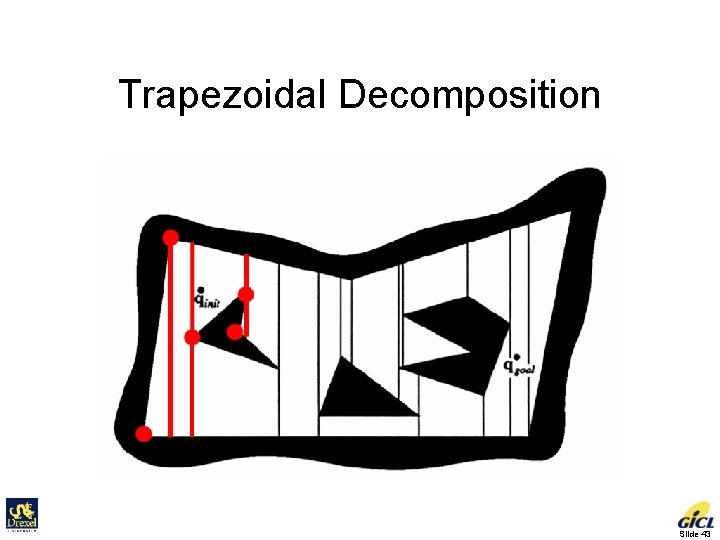
Trapezoidal Decomposition Slide 43

Computational Efficiency • Running time O(n log n) by planar sweep • Space O(n) • Mostly for 2 -D configuration spaces Slide 44
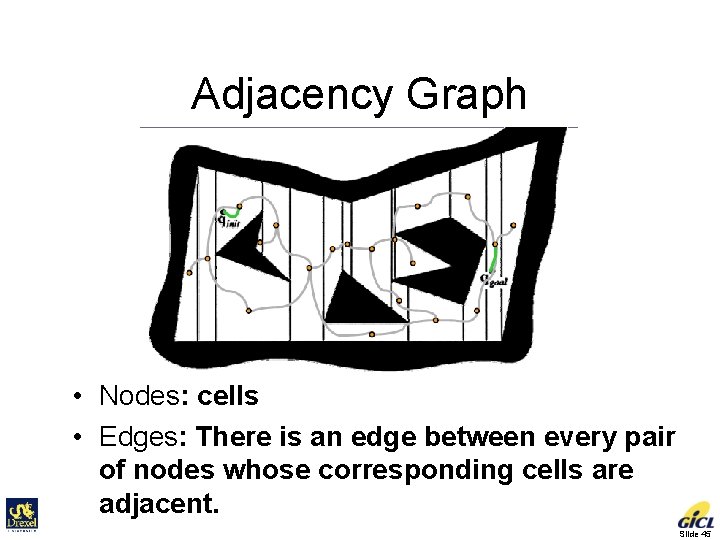
Adjacency Graph • Nodes: cells • Edges: There is an edge between every pair of nodes whose corresponding cells are adjacent. Slide 45

Summary • Discretize the space by constructing an adjacency graph of the cells • Search the adjacency graph Slide 46

Cell-decomposition Methods • Exact cell decomposition • Approximate cell decomposition – F is represented by a collection of nonoverlapping cells whose union is contained in F. – Cells usually have simple, regular shapes, e. g. , rectangles, squares. – Facilitate hierarchical space decomposition Slide 47
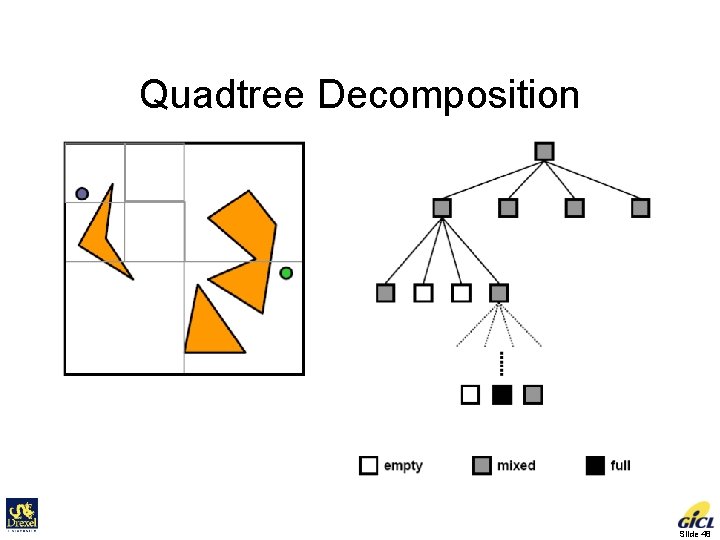
Quadtree Decomposition Slide 48
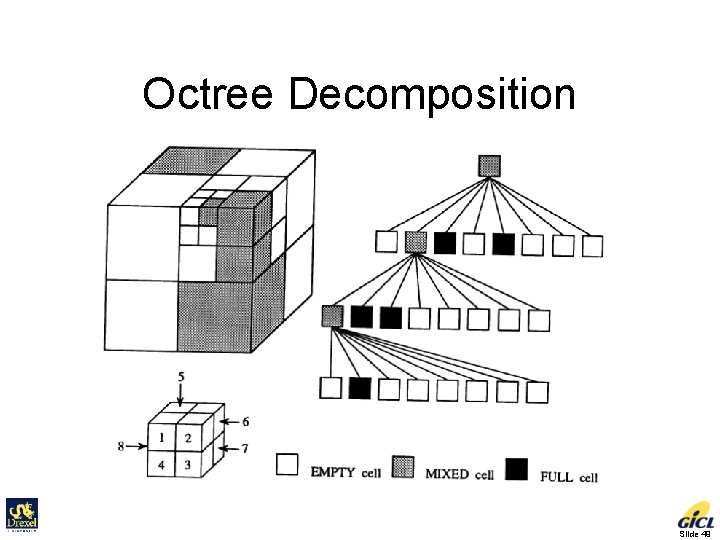
Octree Decomposition Slide 49

Algorithm Outline Slide 50

• Classic Path Planning Approaches Roadmap – Represent the connectivity of the free space by a network of 1 -D curves • Cell decomposition – Decompose the free space into simple cells and represent the connectivity of the free space by the adjacency graph of these cells • Potential field – Define a potential function over the free space that has a global minimum at the goal and follow the steepest descent of the potential function Slide 51
![Potential Fields • Initially proposed for real-time collision avoidance [Khatib 1986]. Hundreds of papers Potential Fields • Initially proposed for real-time collision avoidance [Khatib 1986]. Hundreds of papers](http://slidetodoc.com/presentation_image_h/1f466c3038b2f3ccdc8693758becd507/image-52.jpg)
Potential Fields • Initially proposed for real-time collision avoidance [Khatib 1986]. Hundreds of papers published. • A potential field is a scalar function over the free space. • To navigate, the robot applies a force proportional to the negated gradient of the potential field. • A navigation function is an ideal potential field that – – has global minimum at the goal has no local minima grows to infinity near obstacles is smooth Slide 52
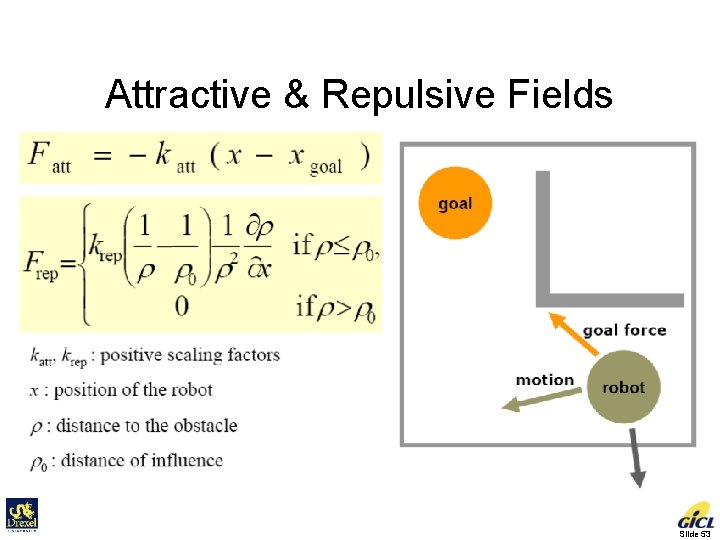
Attractive & Repulsive Fields Slide 53

How Does It Work? Slide 54

Algorithm Outline • Place a regular grid G over the configuration space • Compute the potential field over G • Search G using a best-first algorithm with potential field as the heuristic function Slide 55

Local Minima • What can we do? – Escape from local minima by taking random walks – Build an ideal potential field – navigation function – that does not have local minima Slide 56

Question • Can such an ideal potential field be constructed efficiently in general? Slide 57

Completeness • A complete motion planner always returns a solution when one exists and indicates that no such solution exists otherwise. – Is the visibility graph algorithm complete? Yes. – How about the exact cell decomposition algorithm and the potential field algorithm? Slide 58

Why Complete Motion Planning? • Probabilistic roadmap motion planning • Complete motion planning – Efficient – Work for complex problems with many DOF – Always terminate – Difficult for narrow passages – May not terminate when no path exists – Not efficient – Not robust even for low DOF Slide 59
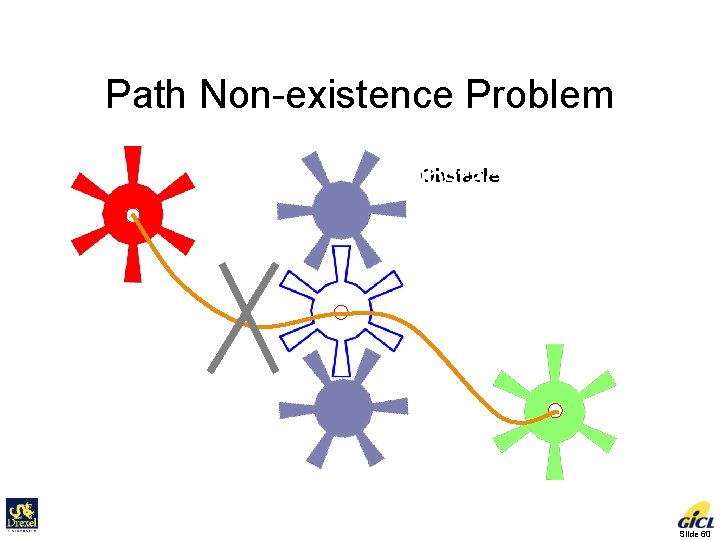
Path Non-existence Problem Robot Initial Obstacle Goal Slide 60
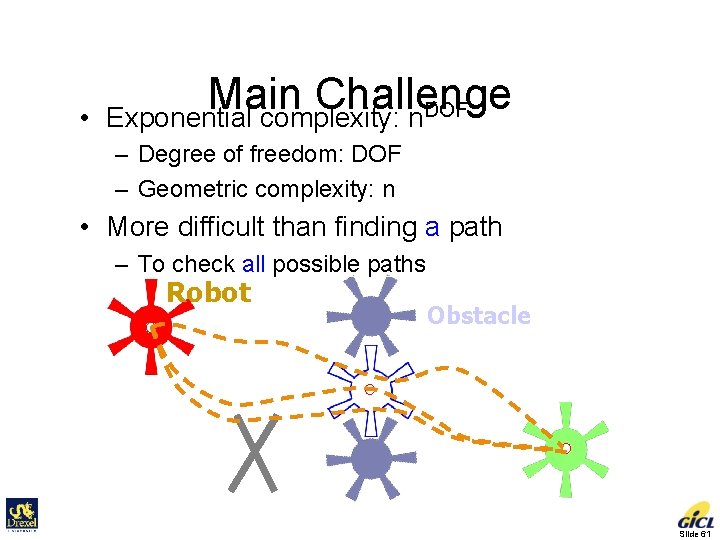
• Main Challenge Exponential complexity: n. DOF – Degree of freedom: DOF – Geometric complexity: n • More difficult than finding a path – To check all possible paths Robot Initial Obstacle Goal Slide 61

Approaches • Exact Motion Planning – Based on exact representation of free space • Approximation Cell Decomposition (ACD) • A Hybrid planner Slide 62
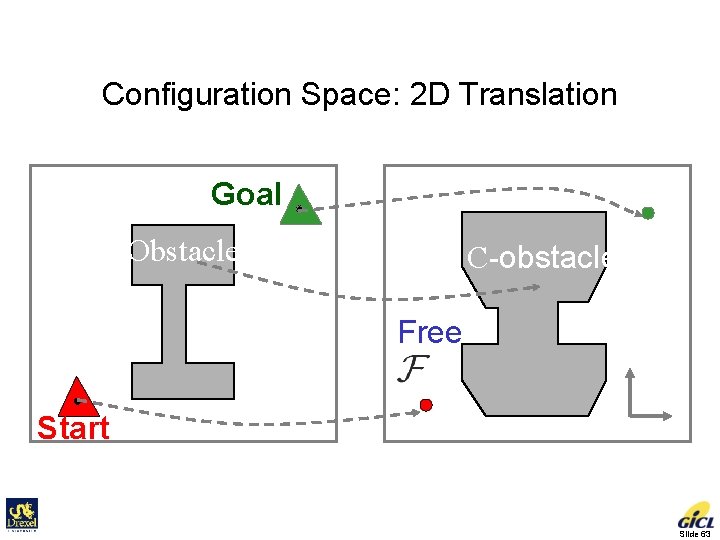
Configuration Space: 2 D Translation Workspace Configuration Space Goal Obstacle Robot Start C-obstacle Free y x Slide 63
![Configuration Space Computation • [Varadhan et al, ICRA 2006] • 2 Translation + 1 Configuration Space Computation • [Varadhan et al, ICRA 2006] • 2 Translation + 1](http://slidetodoc.com/presentation_image_h/1f466c3038b2f3ccdc8693758becd507/image-64.jpg)
Configuration Space Computation • [Varadhan et al, ICRA 2006] • 2 Translation + 1 Rotation • 215 seconds Obstacle y x Robot Slide 64
![Exact Motion Planning • Approaches – Exact cell decomposition [Schwartz et al. 83] – Exact Motion Planning • Approaches – Exact cell decomposition [Schwartz et al. 83] –](http://slidetodoc.com/presentation_image_h/1f466c3038b2f3ccdc8693758becd507/image-65.jpg)
Exact Motion Planning • Approaches – Exact cell decomposition [Schwartz et al. 83] – Roadmap [Canny 88] – Criticality based method [Latombe 99] – Voronoi Diagram – Star-shaped roadmap [Varadhan et al. 06] • Not practical – Due to free space computation – Limit for special and simple objects • Ladders, sphere, convex shapes Slide 65

Approaches • Exact Motion Planning – Based on exact representation of free space • Approximation Cell Decomposition (ACD) • A Hybrid Planner Combing ACD and PRM Slide 66

Approximation Cell Decomposition (ACD) • Not compute the free space exactly at once • But compute it incrementally • Relatively easy to implement – – [Lozano-Pérez 83] [Zhu et al. 91] [Latombe 91] [Zhang et al. 06] Slide 67
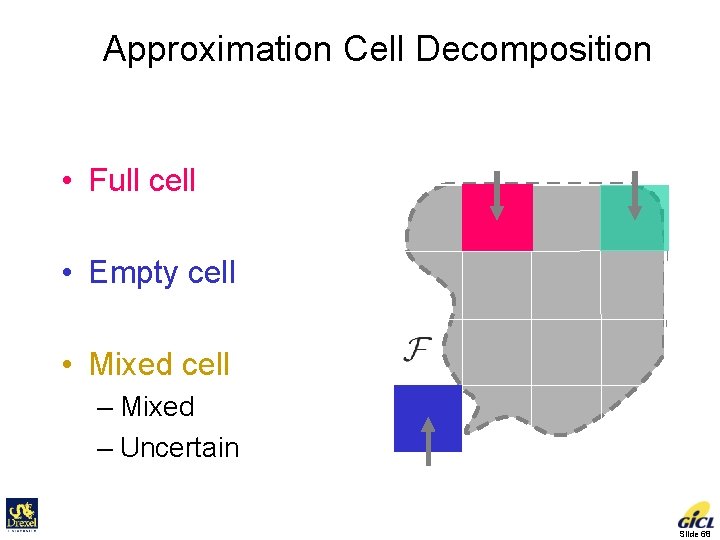
Approximation Cell Decomposition • Full cell Configuration Space full mixed • Empty cell • Mixed cell – Mixed – Uncertain empty Slide 68
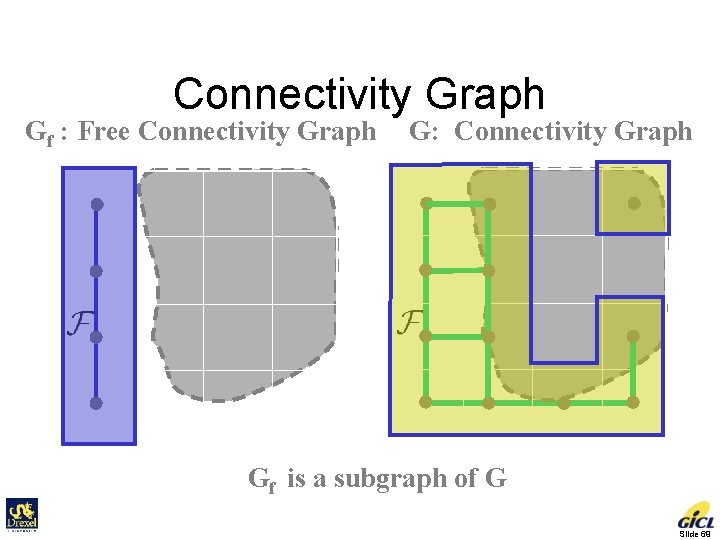
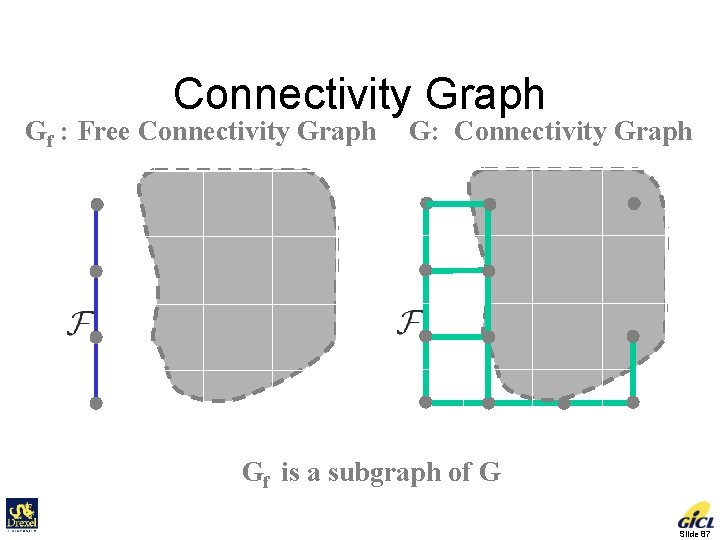
Connectivity Graph Gf : Free Connectivity Graph G: Connectivity Graph Gf is a subgraph of G Slide 69
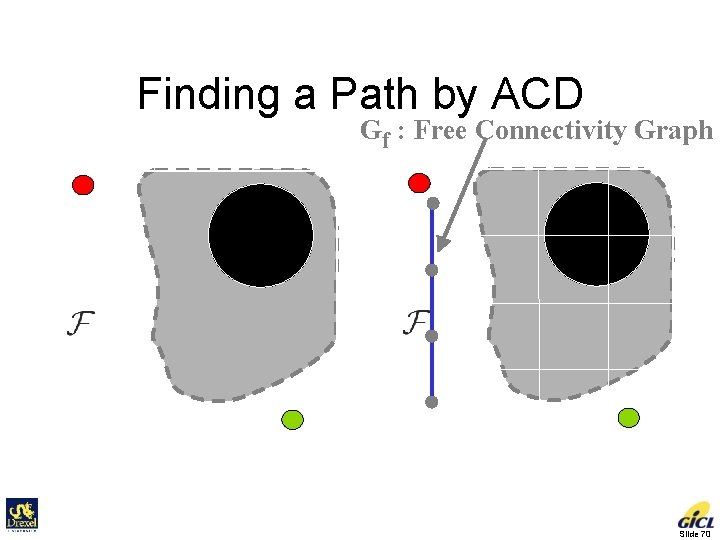
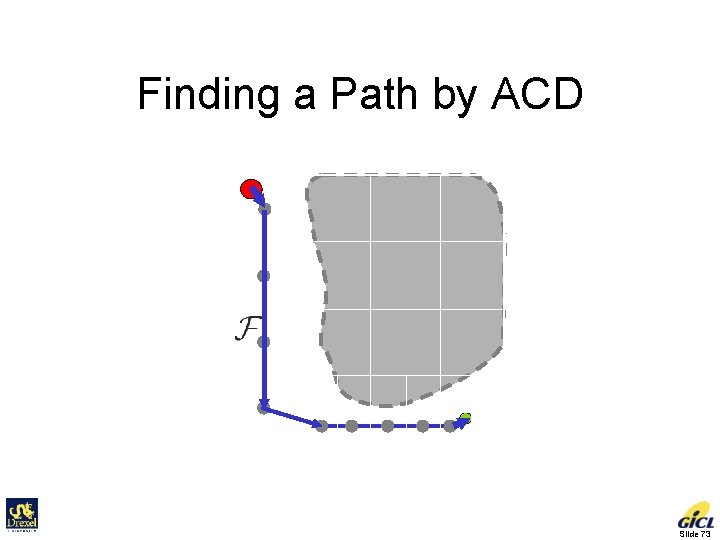
Finding a Path by ACD Gf : Free Connectivity Graph Initial Goal Slide 70
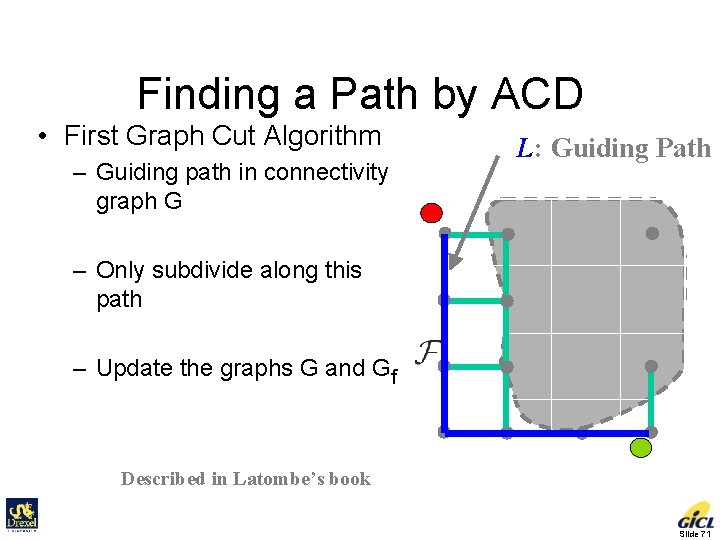
Finding a Path by ACD • First Graph Cut Algorithm – Guiding path in connectivity graph G L: Guiding Path – Only subdivide along this path – Update the graphs G and Gf Described in Latombe’s book Slide 71
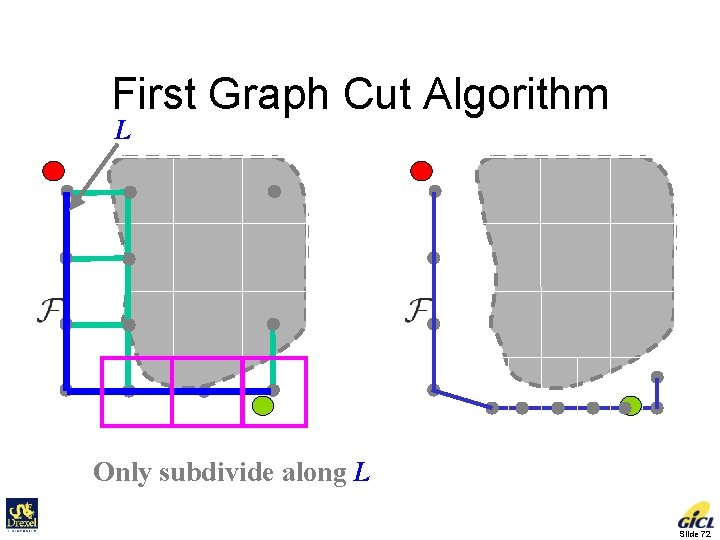
First Graph Cut Algorithm L Only subdivide along L Slide 72
Finding a Path by ACD Slide 73

ACD for Path Non-existence Initial Goal C-space Slide 74
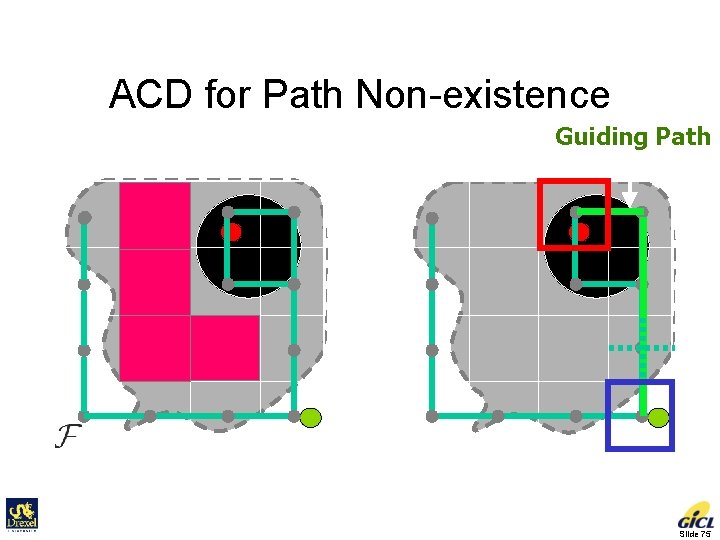
ACD for Path Non-existence Connectivity Graph Guiding Path Slide 75
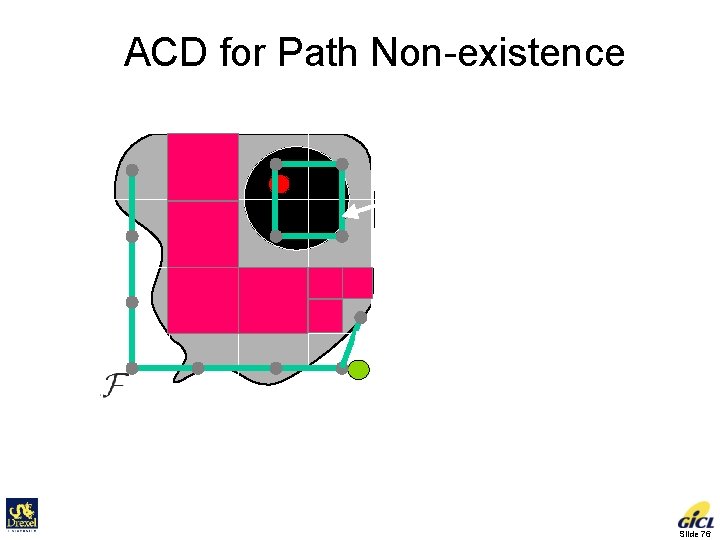
ACD for Path Non-existence Connectivity graph is not connected No path! Sufficient condition for deciding path non-existence Slide 76
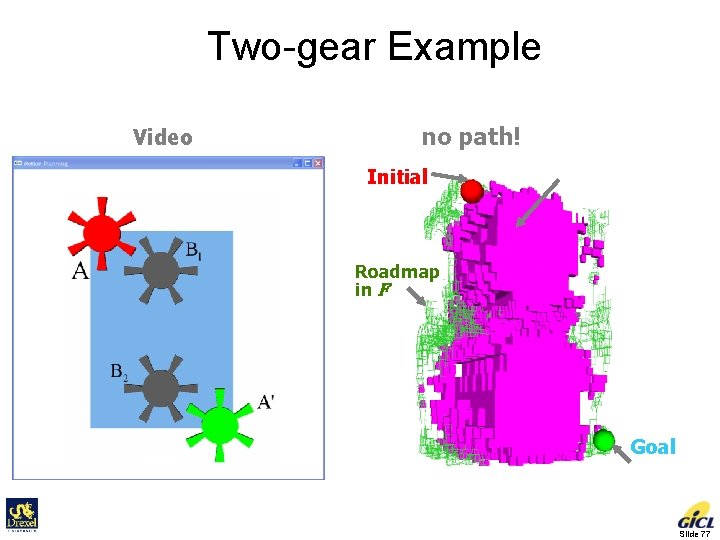
Two-gear Example Video no path! Initial 3. 356 s Cells in C-obstacle Roadmap in F Goal Slide 77
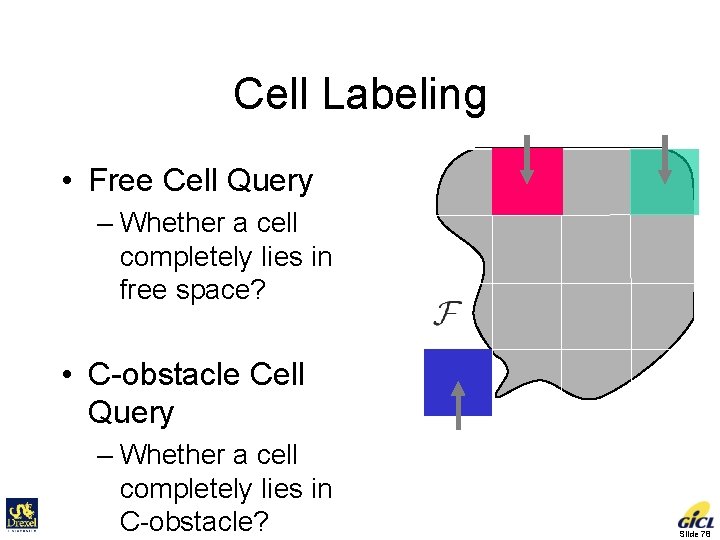
Cell Labeling full mixed • Free Cell Query – Whether a cell completely lies in free space? • C-obstacle Cell Query – Whether a cell completely lies in C-obstacle? empty Slide 78
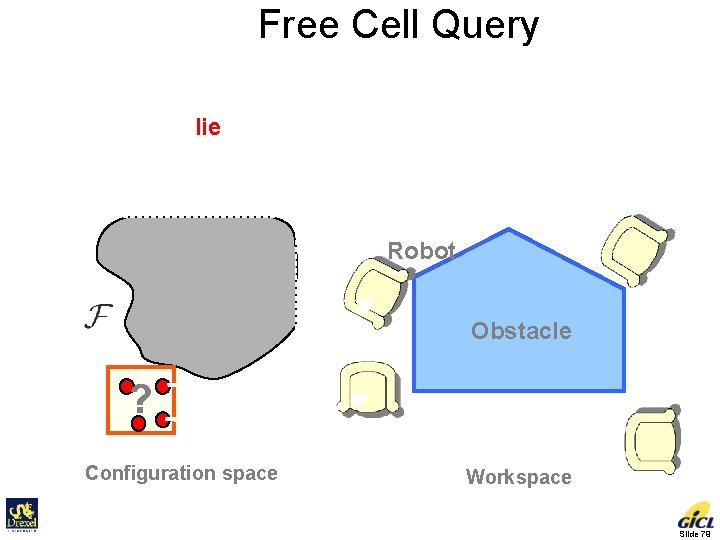
Free Cell Query A Collision Detection Problem • Does the cell lie inside free space? • Do robot and obstacle separate at all configurations? Robot Obstacle ? Configuration space Workspace Slide 79

Clearance • Separation distance – A well studied geometric problem d • Determine a volume in C-space which are completely free Slide 80
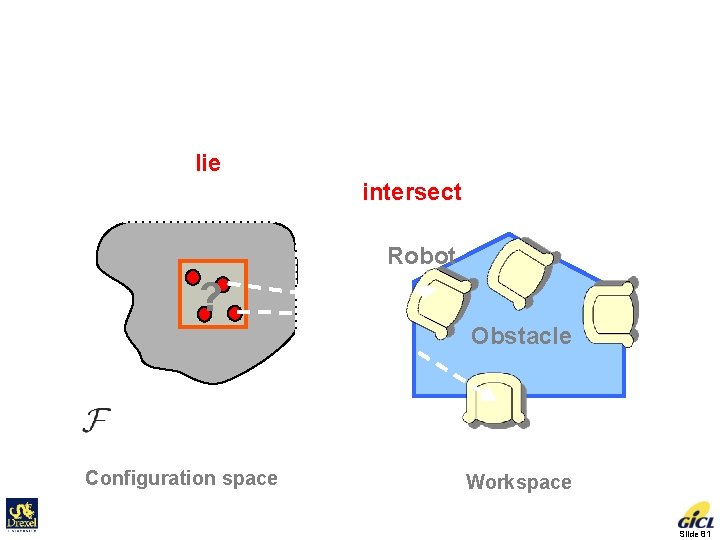
C-obstacle Query Another Collision Detection Problem • Does the cell lie inside C-obstacle? • Do robot and obstacle intersect at all configurations? Robot ? Obstacle Configuration space Workspace Slide 81
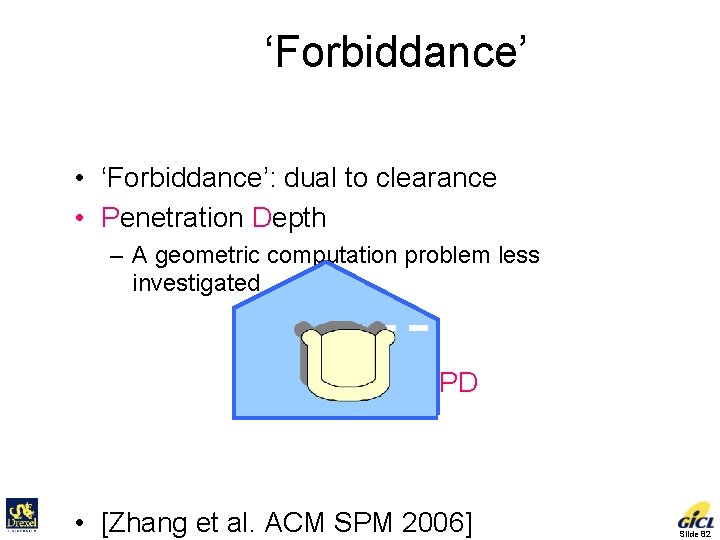
‘Forbiddance’ • ‘Forbiddance’: dual to clearance • Penetration Depth – A geometric computation problem less investigated PD • [Zhang et al. ACM SPM 2006] Slide 82

Limitation of ACD • Combinatorial complexity of cell decomposition • Limited for low DOF problem – 3 -DOF robots Slide 83

Approaches • Exact Motion Planning – Based on exact representation of free space • Approximation Cell Decomposition (ACD) • A Hybrid Planner Combing ACD and PRM Slide 84

• Hybrid Planning • Complete Motion Probabilistic roadmap motion planning Planning + Efficient + Many DOFs + Complete - Narrow passages - Path non-existence - Not efficient Can we combine them together? Slide 85
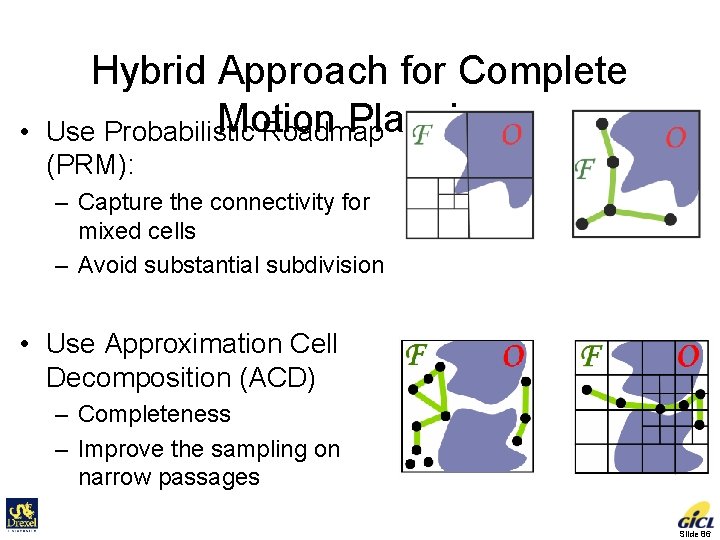
• Hybrid Approach for Complete Motion Planning Use Probabilistic Roadmap (PRM): – Capture the connectivity for mixed cells – Avoid substantial subdivision • Use Approximation Cell Decomposition (ACD) – Completeness – Improve the sampling on narrow passages Slide 86
Connectivity Graph Gf : Free Connectivity Graph G: Connectivity Graph Gf is a subgraph of G Slide 87
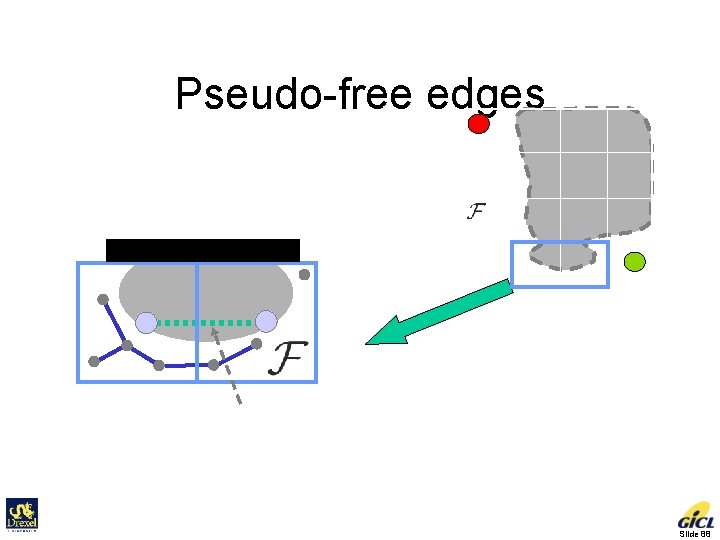
Pseudo-free edges Initial Goal Pseudo free edge for two adjacent cells Slide 88
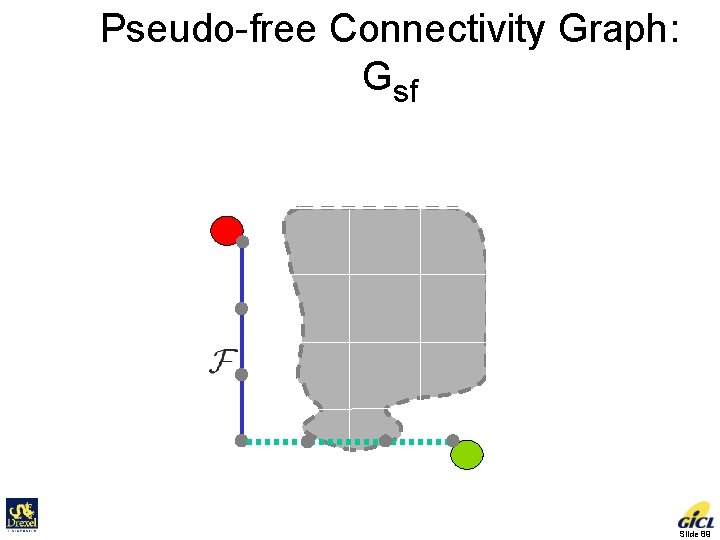
Pseudo-free Connectivity Graph: Gsf = Gf + Pseudo-edges Initial Goal Slide 89
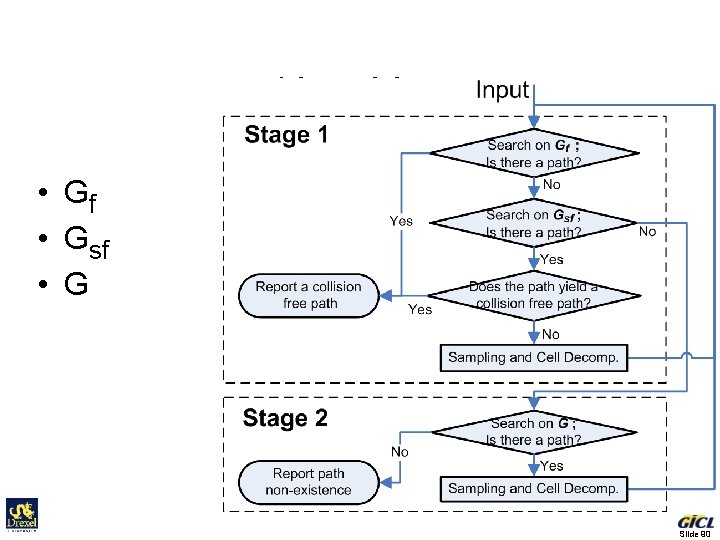
Algorithm • Gf • Gsf • G Slide 90

Results of Hybrid Planning Slide 91

Results of Hybrid Planning Slide 92
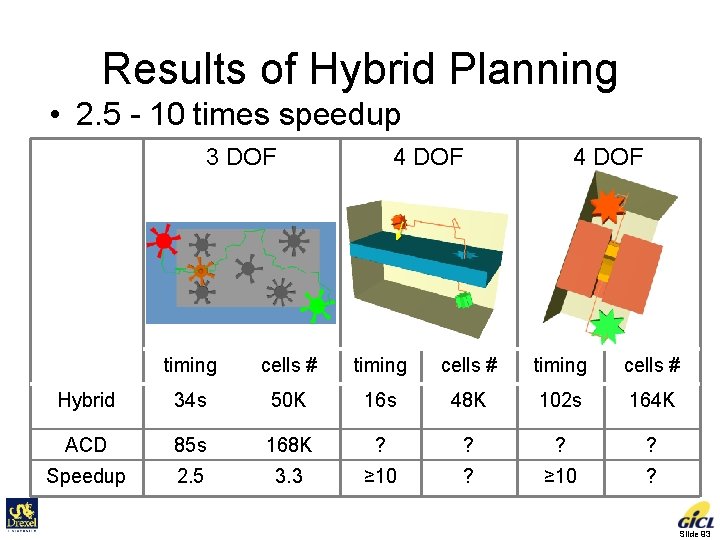
Results of Hybrid Planning • 2. 5 - 10 times speedup 3 DOF 4 DOF timing cells # Hybrid 34 s 50 K 16 s 48 K 102 s 164 K ACD 85 s 168 K ? ? Speedup 2. 5 3. 3 ≥ 10 ? Slide 93

Summary • Difficult for Exact Motion Planning – Due to the difficulty of free space configuration computation • ACD is more practical – Explore the free space incrementally • Hybrid Planning – Combine the completeness of ACD and efficiency of PRM Slide 94
- Slides: 94