Robot Inverse Kinematics Lectures 7 8 Dr Wajdi

Robot Inverse Kinematics Lectures 7 & 8 Dr. Wajdi Sadik • P&O Eng. , Al-Nahrain University • 1

Inverse Kinematics Given a desired position (P) & orientation (R) of the end-effector Find the joint variables which can bring the robot to the desired configuration. 2

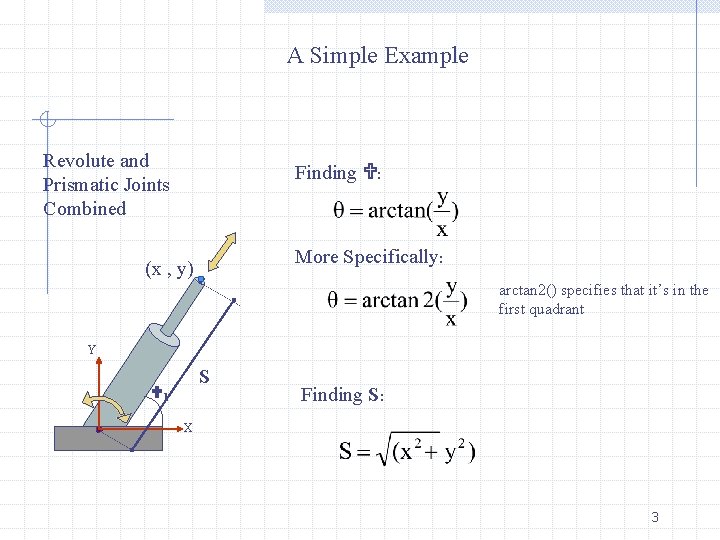
A Simple Example Revolute and Prismatic Joints Combined Finding : More Specifically: (x , y) arctan 2() specifies that it’s in the first quadrant Y S 1 Finding S: X 3

What is Atan 2 4

5

6

7

Solvability Given the numerical value of find values of we attempt to The PUMA 560: Given as numerical values, solve for 6 joint angles, 12 equations and 6 unknowns 6 equations and 6 unknowns (nonlinear, transcendental equations) 8

Inverse Kinematics More difficult. n n The equations to solve are nonlinear thus systematic closedform solution is not always available. Solution not unique. w Redundant robot. w Elbow-up/elbow-down configuration. n Robot dependent. 2 solutions! 9

The Workspace: volume of space which can be reached by the end effector Dextrous workspace: volume of space where the end effector can be arbitrarily oriented Reachable workspace: volume of space which the robot can reach in at least one orientation 10

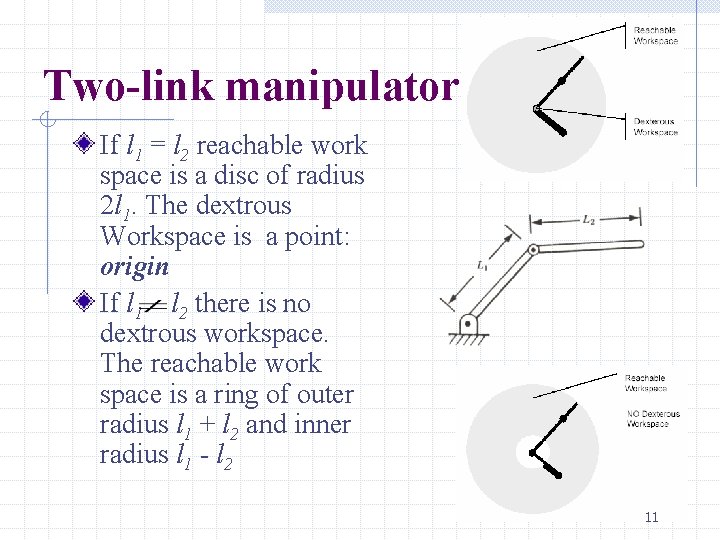
Two-link manipulator If l 1 = l 2 reachable work space is a disc of radius 2 l 1. The dextrous Workspace is a point: origin If l 1 l 2 there is no dextrous workspace. The reachable work space is a ring of outer radius l 1 + l 2 and inner radius l 1 - l 2 11

Existence of Solutions A solution to the IKP exists if the target belongs to the workspace. Workspace computation may be hard. In practice it is made easy by special design of the robot. 12

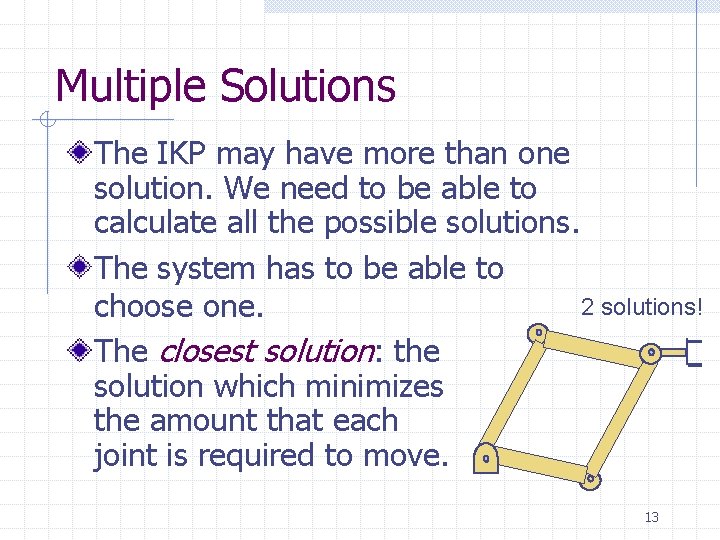
Multiple Solutions The IKP may have more than one solution. We need to be able to calculate all the possible solutions. The system has to be able to 2 solutions! choose one. The closest solution: the solution which minimizes the amount that each joint is required to move. 13

The Closest Solution in Joint Space Weights might be applied. Selection favors moving smaller joints rather than moving larger joints when a choice exist. The presence of obstacles. 14

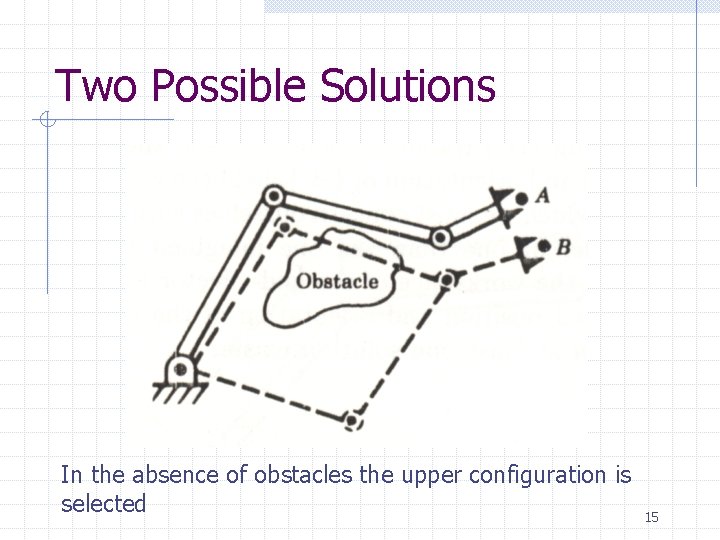
Two Possible Solutions In the absence of obstacles the upper configuration is selected 15

Number of Solutions Depends upon the number and range of joints and also is a function of link parameters , a, d 8 solutions exits Another 4 solution 4 Solutions of the PUMA 560 16

Number of Solutions vs. Nonzero ai The more the link length parameters are nonzero, the bigger the maximum number of solutions! 17

Solvability All systems with revolute and prismatic joints having total of 6 D. O. F in a single series chain are solvable. But this general solution is a numerical one. Robots with analytic solution: several intersecting joint axes and/or many i = 0, 90 o. 18

Methods of Solutions A manipulator is solvable if the joint variables can be determined by an algorithm. The algorithm should find all possible solutions. • Solutions closed form solutions numerical solutions 19

Numerical Solutions Results in a numerical, iterative solution to system of equations, for example Newton/Raphson techniques. Unknown number of operations to solve. Only returns a single solution. Accuracy is dictated by user. Because of these reasons, this is much less desirable than a closed-form solution. Can be applied to all robots. 20

Closed-form solutions Analytical solution to system of equations Can be solved in a fixed number of operations (therefore, computationally fast/known speed) Results in all possible solutions to the manipulator kinematics Often difficult or impossible to find Most desirable for real-time control Most desirable overall 21

Closed-form solutions Given a 6 axis robot. It can be proven that there exists a closed form solution for inverse kinematics: w If three adjacent revolute joint axes intersect at a point (PUMA, Stanford). w If three adjacent revolute joint axes are parallel to one another (MINIMOVER). In any case algebraic or geometric intuition is required to obtain closed form solutions. 22

Methods of Solutions In general the IK problem can be solved by various methods such as: Inverse Transform ( Paul, 1981) Screw Algebra (Kohli 1975) Dual Matrices (Denavit 1956) Iterative (Uicker 1964) Geometric approach (Lee 1984) Decoupling of position and orientation (Pieper 1968) 23

Closed-form Solutions We are interested in closed-form solutions: 1. Algebraic methods 2. Geometric methods 24