Robosnail 1 SnailInspired Fluid Locomotion Brian Chan M

Robosnail 1 Snail-Inspired Fluid Locomotion Brian Chan, M. S Theresa Guo, undergraduate researcher Advisors: Anette Hosoi, Julio Guerrero (SLB) Hatsopolous Microfluids Laboratory Department of Mechanical Engineering Massachusetts Institute of Technology Schlumberger - Doll Research, SDR

Contents: n n n Snail locomotion Type 1 Robosnails ¨ Theory ¨ Simulations Robosnail 1 A ¨ Design ¨ Experiment Robosnail 1 B ¨ Design ¨ Experiment Robosnail 1 C ¨ In progress Conclusions Robosnail 1 A Robosnail 1 B

Motivation To evaluate the feasibility of using snail-like locomotion, and to optimize the performance of mechanical Robosnails. Advantages of snail locomotion: n can be configured as a versatile flexible robot n A sealed Robosnail mechanism can be robust in muddy conditions n Effective locomotion for environments with little or no traction

Snail Locomotion basics - All snails are separated from the substrate by a fluid layer (mucus) Locomotive forces must be transferred through this layer to the substrate Snails, equipped with a single flexible foot must find a way to generate fluid forces parallel to the substrate.

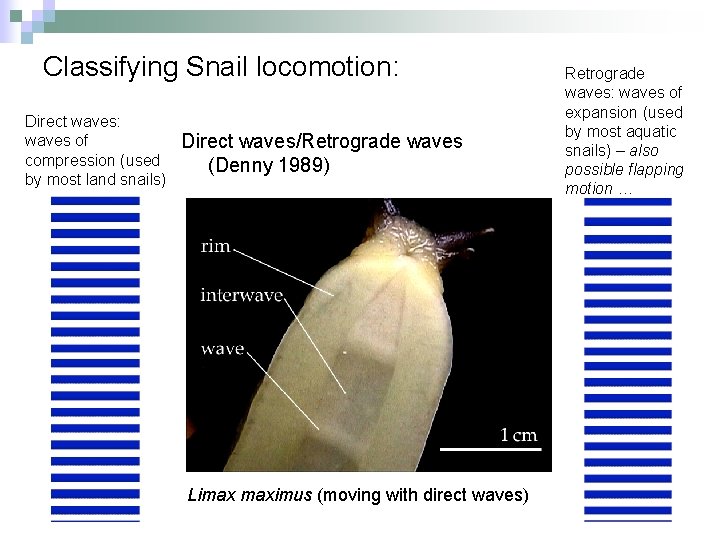
Classifying Snail locomotion: Direct waves: waves of compression (used by most land snails) Direct waves/Retrograde waves (Denny 1989) Limax maximus (moving with direct waves) Retrograde waves: waves of expansion (used by most aquatic snails) – also possible flapping motion …

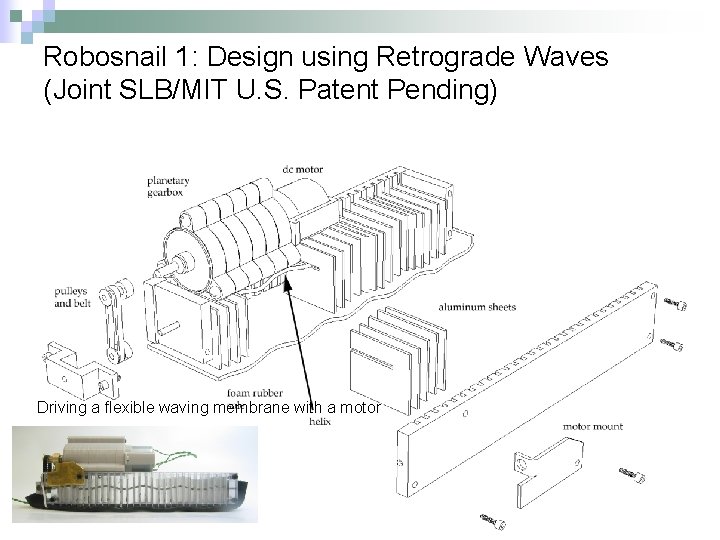
Robosnail 1: Design using Retrograde Waves (Joint SLB/MIT U. S. Patent Pending) Driving a flexible waving membrane with a motor

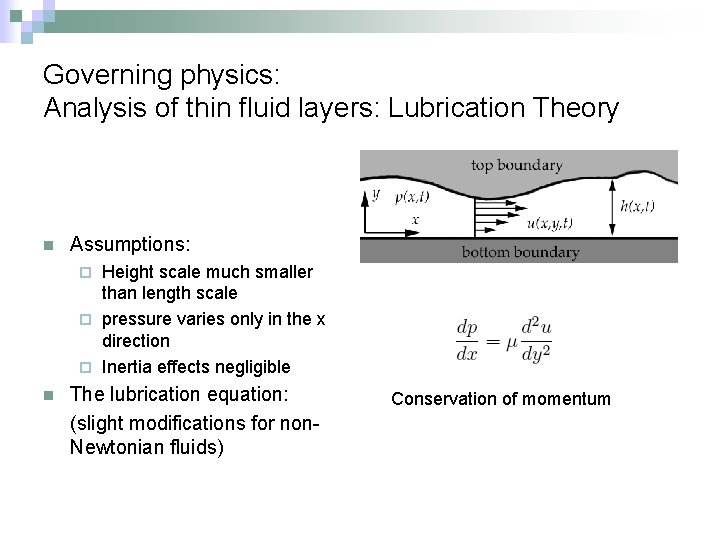
Governing physics: Analysis of thin fluid layers: Lubrication Theory n Assumptions: Height scale much smaller than length scale ¨ pressure varies only in the x direction ¨ Inertia effects negligible ¨ n The lubrication equation: (slight modifications for non. Newtonian fluids) Conservation of momentum

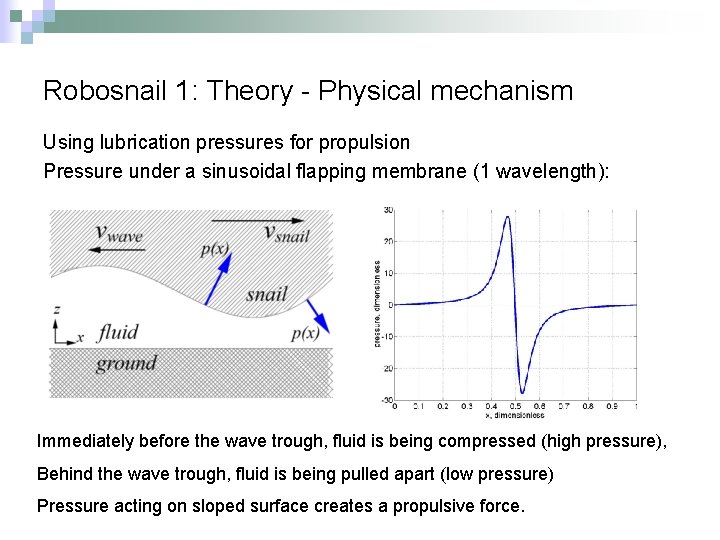
Robosnail 1: Theory - Physical mechanism Using lubrication pressures for propulsion Pressure under a sinusoidal flapping membrane (1 wavelength): Immediately before the wave trough, fluid is being compressed (high pressure), Behind the wave trough, fluid is being pulled apart (low pressure) Pressure acting on sloped surface creates a propulsive force.

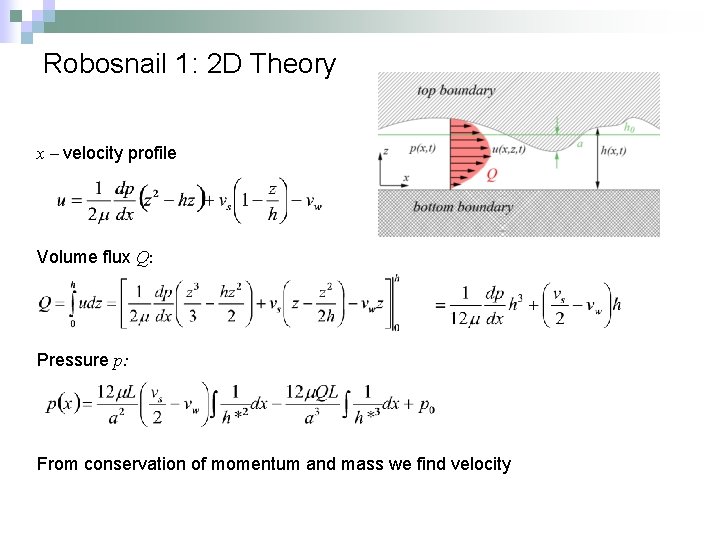
Robosnail 1: 2 D Theory x – velocity profile Volume flux Q: Pressure p: From conservation of momentum and mass we find velocity

Robosnail 1: 2 D Theory Steady- state horizontal force balance: horizontal component of pressure force and shear stress at membrane balances tractoring force

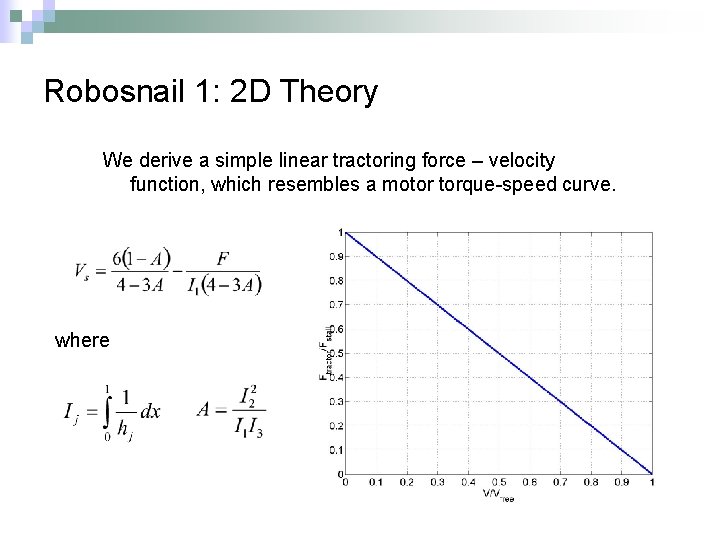
Robosnail 1: 2 D Theory We derive a simple linear tractoring force – velocity function, which resembles a motor torque-speed curve. where

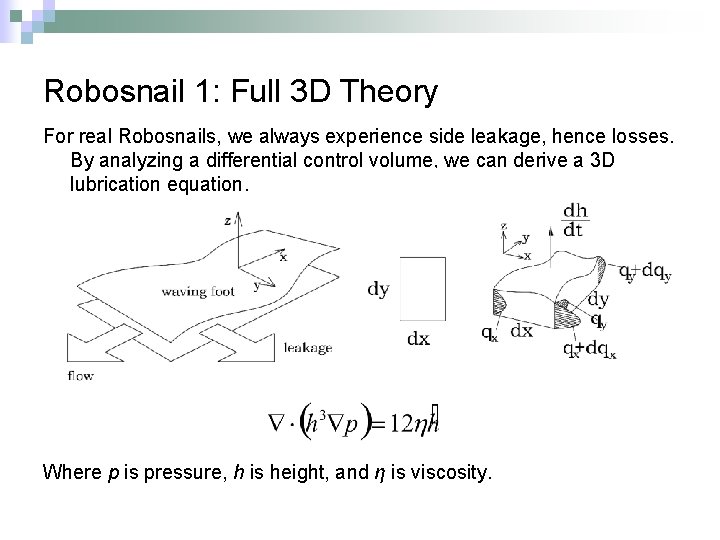
Robosnail 1: Full 3 D Theory For real Robosnails, we always experience side leakage, hence losses. By analyzing a differential control volume, we can derive a 3 D lubrication equation. Where p is pressure, h is height, and η is viscosity.

Robosnail 1: Full 3 D Theory Deriving a force-speed relationship [A]: stalled robosnail [B] pure shearing force In 3 D, the force-velocity relationship is still linear

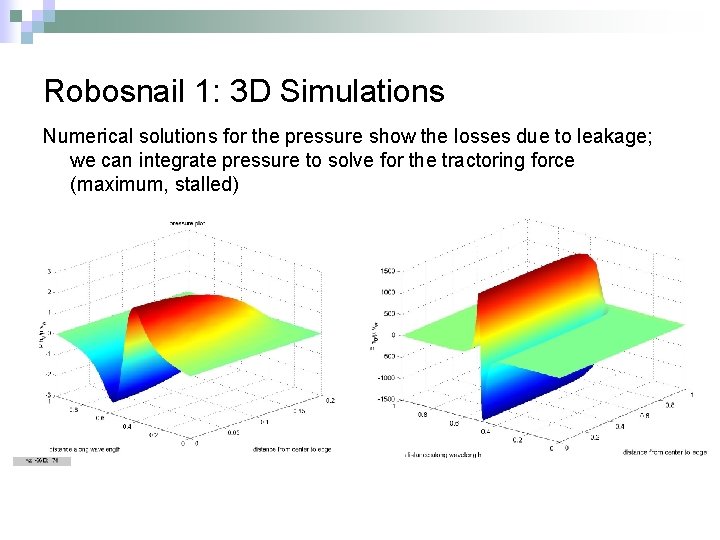
Robosnail 1: 3 D Simulations Numerical solutions for the pressure show the losses due to leakage; we can integrate pressure to solve for the tractoring force (maximum, stalled)

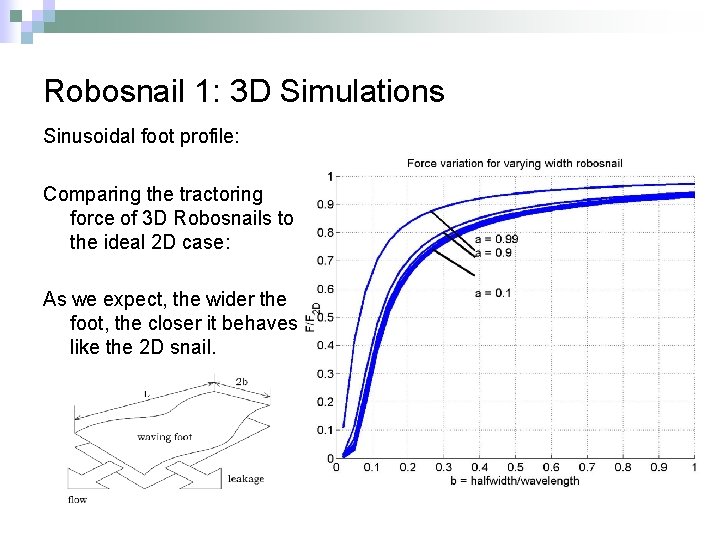
Robosnail 1: 3 D Simulations Sinusoidal foot profile: Comparing the tractoring force of 3 D Robosnails to the ideal 2 D case: As we expect, the wider the foot, the closer it behaves like the 2 D snail.

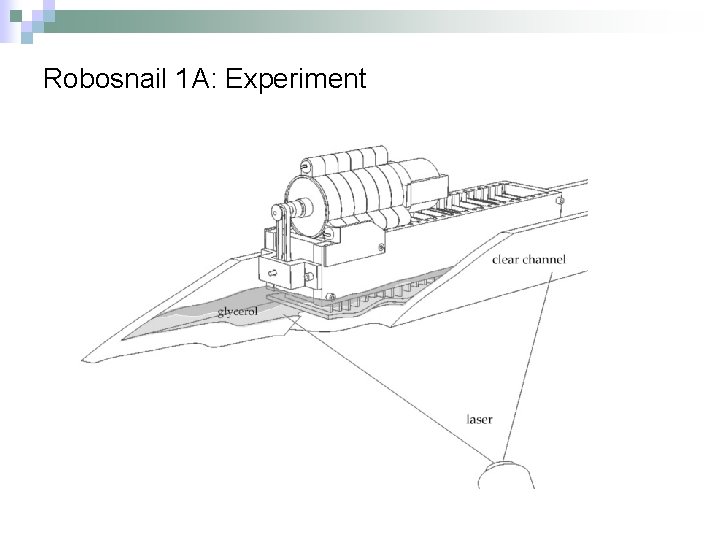
Robosnail 1 A: Experiment

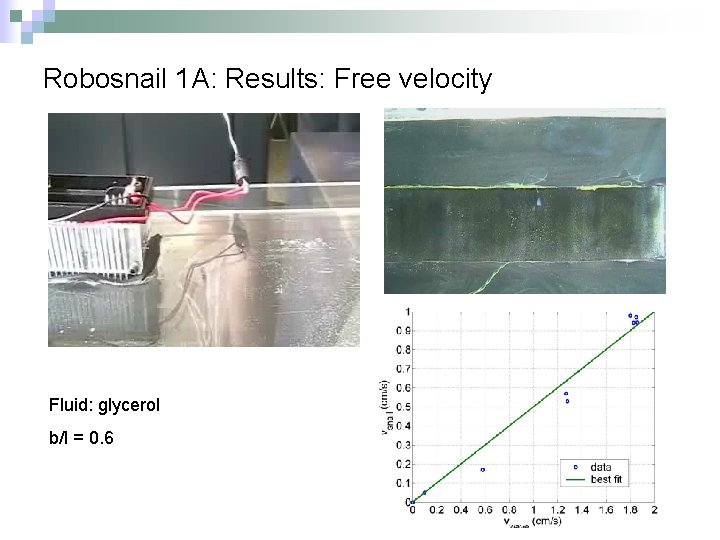
Robosnail 1 A: Results: Free velocity Fluid: glycerol b/l = 0. 6

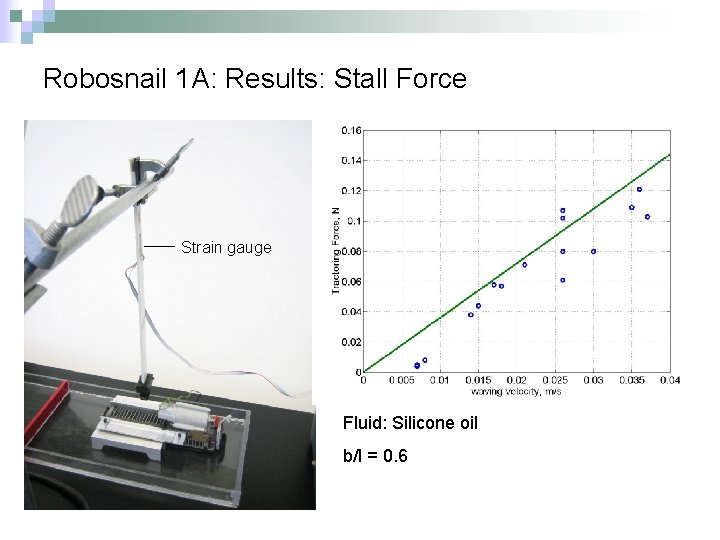
Robosnail 1 A: Results: Stall Force Strain gauge Fluid: Silicone oil b/l = 0. 6

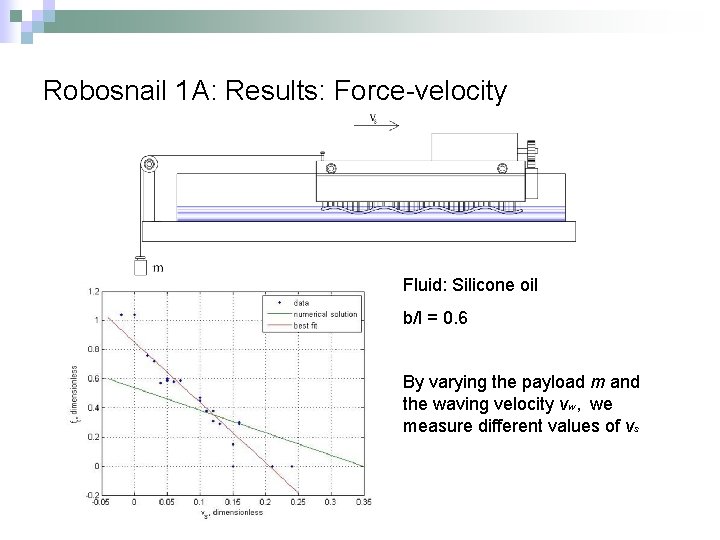
Robosnail 1 A: Results: Force-velocity Fluid: Silicone oil b/l = 0. 6 By varying the payload m and the waving velocity vw, we measure different values of vs

Robosnail 1 B: Apparatus - - Periodic foot design to eliminate entrance/exit anomalies. Replaceable tracks define the height profile.

Robosnail 1 B: Apparatus Core mechanism: Various replaceable tracks:

Robosnail 1 B: Experiment

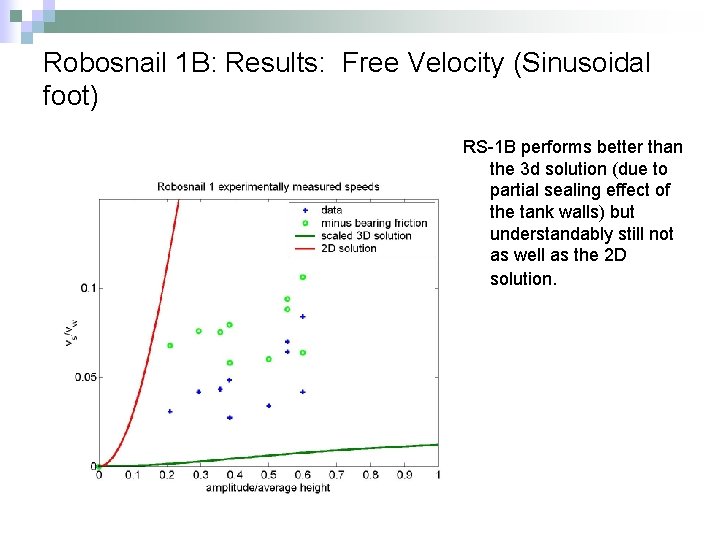
Robosnail 1 B: Results: Free Velocity (Sinusoidal foot) RS-1 B performs better than the 3 d solution (due to partial sealing effect of the tank walls) but understandably still not as well as the 2 D solution.

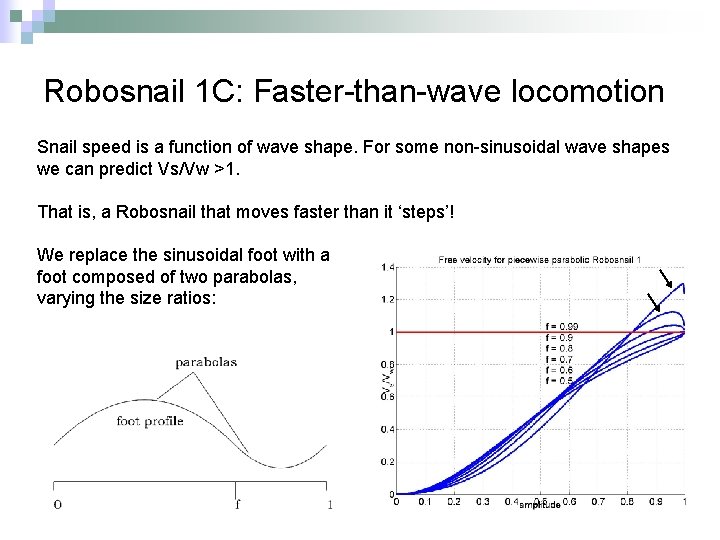
Robosnail 1 C: Faster-than-wave locomotion Snail speed is a function of wave shape. For some non-sinusoidal wave shapes we can predict Vs/Vw >1. That is, a Robosnail that moves faster than it ‘steps’! We replace the sinusoidal foot with a foot composed of two parabolas, varying the size ratios:

Conclusions - Lubrication theory predicts a linear force and velocity relationship for both 2 D and 3 D Robosnails. - Analytic solutions exist for the 2 D case for any given wave height function. - Numerical simulations give a similar linear force-velocity relation for 3 D snails, but with losses dependent on the ratio of snail width to length. - We have experimental data for sinusoidal wave Robosnails that confirms the numerical results. - In theory, certain wave shapes exhibit regimes where the snail speed is faster than the wave speed; future experiments will test this theory.

Appendix: 2 D theory (detail) To more easily analyze the fluid flow in the lubrication layer we switch to a reference frame following the waves. In the new reference frame, Q = constant.

Appendix: Dimensionless variables Experimental constants: L μ h 0 vw wavelength viscosity average fluid thickness waving velocity Dimensionless variables x = x*/L b = b*/L p= Dimensional variables: x* b* p* h* a* v s* Fx* x-position half-width of foot pressure height foot amplitude snail velocity tractoring force h = h*/h 0 a = a*/h 0 vs= vs*/ vw Fx=

Acknowledgements n National Science Foundation n Schlumberger Limited

References A. Ajdari and H. A. Stone. “A note on swimming using internally generated traveling waves”. Physics of Fluids, 11: 1275– 1277, 1999. B. Chan, N. Balmforth and A. E. Hosoi. “Building a better snail: Lubrication and adhesive locomotion. Physics of Fluids, 17: 111, 113101, 2005. S. Childress. The Mechanics of Swimming and Flying. Cambridge University Press, Cambridge, 1997. M. Denny. “A quantitative model for the adhesive locomotion of the terrestrial slug, Ariolimax columbianus”. Journal of Experimental Biology, 91: 195– 217, 1981. M. Denny. “Mechanical properties of pedal mucus and their consequences for gastropod structure and performance”. American Zoology, 24: 23– 36, 1984. M. Denny. “Invertebrate mucous secretions: functional alternatives to vertebrate paradigms”. Journal of Experimental Biology, pages 337– 366, 1989. AI Dobrolyubov and G Douchy. “Peristaltic transport as the travelling deformation waves”. Journal of Theoretical Biology, 219: 55– 61, 2002. Becker L. E. , Koehler S. A. , and H. A. Stone. “On Self-Propulsion of Micro-Machines at Low Reynolds Number: Purcell’s Three-Link Swimmer”. Journal of Fluid Mechanics, 490: 15– 35, 2003. E. M. Purcell. “Life at Low Reynolds Number”. American Journal of Physics, 45: 3– 11, 1977. DD Spain and WM Kier. “Peristaltic locomotion in holothuroids (Echinodermata)”. Integr. Comp. Biol, 42: 1316– 1316, 2002.