RNEKLEME DAILILARI VE TAHMNLEYCLERN ZELLKLER Do Dr Ali

ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ • Doç. Dr. Ali Kemal ŞEHİRLİOĞLU 1

TEMEL KAVRAMLAR PARAMETRE: • Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. • Ana kütledeki tek bir eleman dahi işlemin dışında kalır ise elde edilen sonuç parametre olarak kabul edilemez. ÖRNEK İSTATİSTİĞİ (PARAMETRE TAHMİNLEYİCİSİ): • Bir örneğin sayısal betimsel ölçüsüdür ve örnekteki gözlemlerden hesaplanır. • Diğer bir deyişle bilinmeyen bir parametrenin sayısal değerini bulabilmek (tahminlemek) için kullanılır. 2

PARAMETRE VE ÖRNEK İSTATİSTİKLERİ İÇİN ÖRNEKLER Parametre • Anakütle ortalaması • Anakütle Medyan M • Anakütle Varyansı 2 • Anakütle Standart sapması • Anakütle Oranı P Örnek istatistiği • Örnek ortalaması • Örnek Medyanı • Örnek Varyansı • Örnek Standart sapması • Örnek Oranı m s 2 s p 3

Bir Populasyon Parametresi Hakkında En Geniş Bilgiyi Hangi Örnek İstatistiğinin İçerdiğine Nasıl Karar Verilecek? Örneğin anakütle ortalaması için • Aritmetik ortalama • Geometrik ortalama • Harmonik ortalama • Medyan vb. örnek istatistiklerinden hangisi tercih edilmelidir. 4

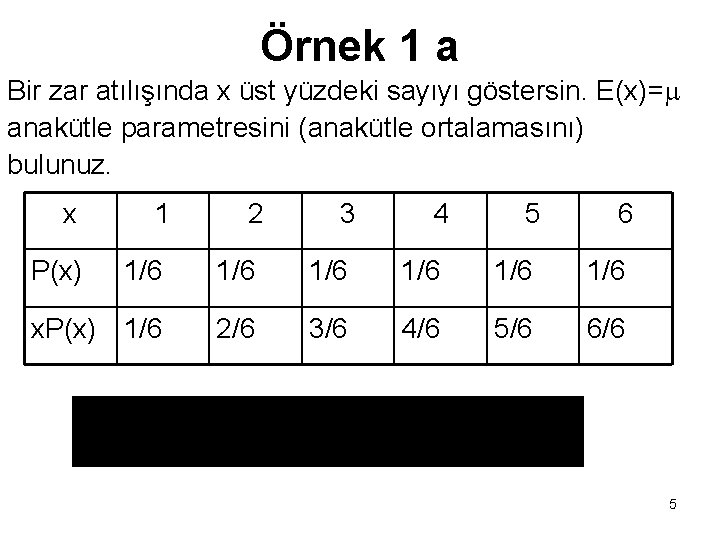
Örnek 1 a Bir zar atılışında x üst yüzdeki sayıyı göstersin. E(x)= anakütle parametresini (anakütle ortalamasını) bulunuz. x 1 2 3 4 5 6 P(x) 1/6 1/6 1/6 x. P(x) 1/6 2/6 3/6 4/6 5/6 6/6 5

Örnek 1 b • Ancak bu değerinin bir an için bilinmediği ve bunu tahmin etmek için populasyondan 3 örnek alındığını varsayılsın. 6

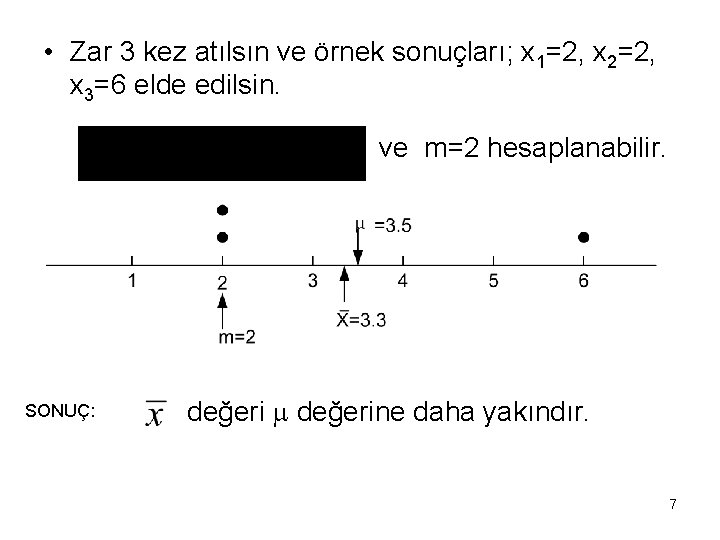
• Zar 3 kez atılsın ve örnek sonuçları; x 1=2, x 2=2, x 3=6 elde edilsin. ve m=2 hesaplanabilir. SONUÇ: değerine daha yakındır. 7

• Zar 3 kez daha atılsın ve örnek sonuçları; x 1=3, x 2=4, x 3=6 elde edilsin. ve m=4 SONUÇ: m değerine daha yakındır. 8

Örnek İçin Yorum 1. Örnekten hesaplanan örnek istatistikleri (tahminleyiciler) birer şans değişkenidir. 2. Ne örnek aritmetik ortalaması Ne de örnek medyanı (m) , populasyon ortalamasına daima daha yakındır denilemez. Sonuçların genellenebilmesi için örnek istatistiklerinin dağılışına gerek duyulmaktadır. 9

ÖRNEKLEME DAĞILIMLARI 10

ÖRNEKLEME DAĞILIMLARI 11

ÖRNEKLEME DAĞILIMLARI 12

ÖRNEK İSTATİSTİKLERİNİNTAHMİNLEYİCİLERİN ÖZELLİKLERİ 13

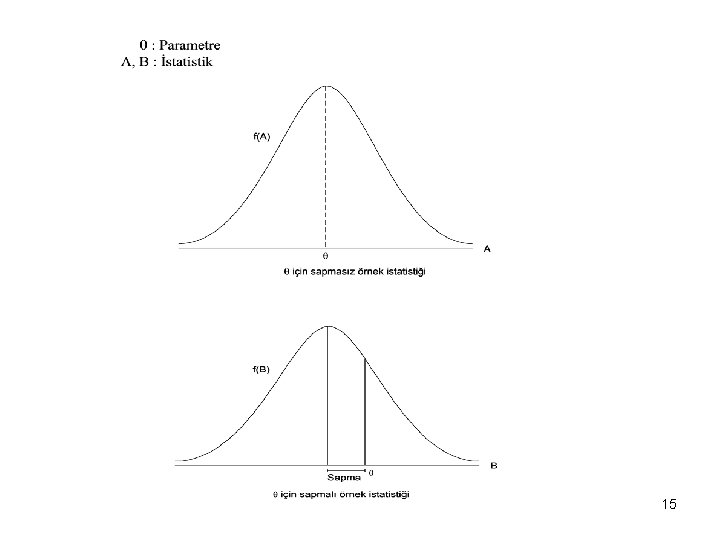
SAPMASIZLIK 14

15

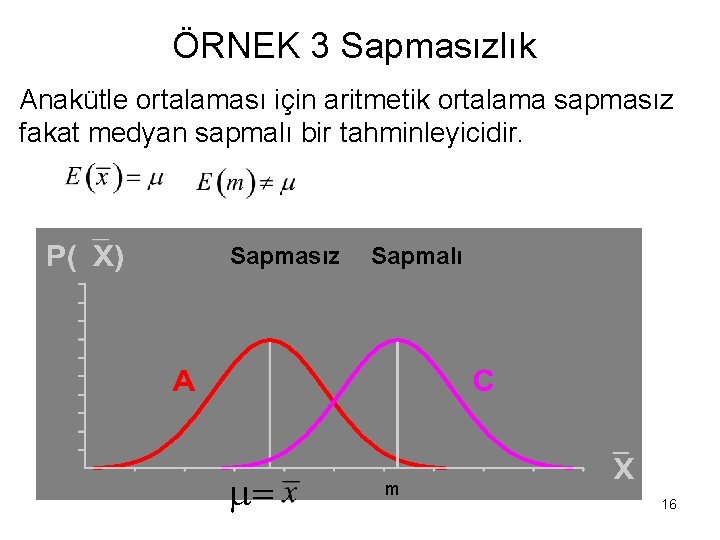
ÖRNEK 3 Sapmasızlık Anakütle ortalaması için aritmetik ortalama sapmasız fakat medyan sapmalı bir tahminleyicidir. Sapmasız = Sapmalı m 16

MİNİMUM VARYANS 17

ÖRNEK: MİNİMUM VARYANS 18

ÖRNEK: ETKİN TAHMİNLEYİCİ 19

ÖRNEK: ETKİN TAHMİNLEYİCİ Ortalamanın örnekleme dağılışı Medyanın örnekleme dağılışı 20

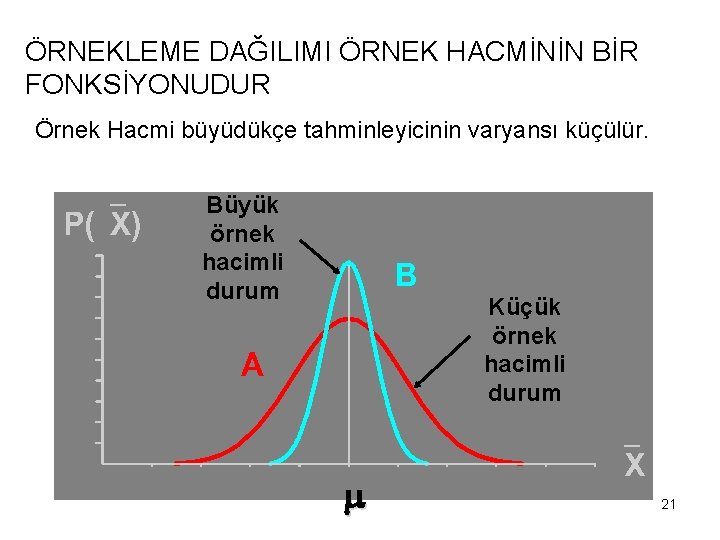
ÖRNEKLEME DAĞILIMI ÖRNEK HACMİNİN BİR FONKSİYONUDUR Örnek Hacmi büyüdükçe tahminleyicinin varyansı küçülür. Büyük örnek hacimli durum Küçük örnek hacimli durum 21

ÖRNEK : 22

ÖRNEK : 23

ÖRNEK 3: 24

ÖRNEK : 25

ÖRNEK 3: 26

ÖRNEK : 27

ÖRNEK 3 28

ÖRNEK 3 29

ÖRNEK 3 30

BEKLENEN DEĞER VE VARYANS OPERATÖRLERİNİN ÖZELLİKLERİ 31

BEKLENEN DEĞER VE VARYANS OPERATÖRLERİNİN ÖZELLİKLERİ 32

MERKEZİ LİMİT TEOREMİ 33

Şans Değişkenlerinin Standartlaştırılması • Standart değişkenler genellikle z ile gösterilir. • ortalaması sıfır, E(z)=0 • Varyansı bir, V(Z)=1. 34

35

BİR DAĞILIMIN BELİRLENMESİ • Dağılışın tipinin belirlenmesi, (Normal, Üstel, Poisson vb. ) • Dağılımın parametrelerinin belirlenmesi 36

37

DAĞILIMIN TİPİ • Merkezi limit teoremine göre aritmetik ortalamanın dağılımı yaklaşık olarak normal dağılıma sahiptir. • Normal dağılımın parametreleri: – Anakütle ortalaması – Anakütle varyansı 38

Dağılımın Parametreleri: Aritmetik Ortalama için Anakütle Ortalaması 39

Dağılımın Parametreleri: Aritmetik Ortalama için Anakütle Varyansı 40

41

Aritmetik Ortalamanın Standartlaştırılması 42

Normal olmayan dağılışlardan örnekleme • Merkezi eğilim Anakütle dağılışı • Yayılma Örnekleme dağılışı – Yerine koyarak örnekleme n=4 X = 5 n =30 X = 1. 8 43

Normal dağılış gösteren bir anakütleden örnekleme • Merkezi eğilim Anakütle dağılışı • Yayılma Örnekleme dağılışı Yerine konularak örnekleme n=4 X = 5 n =16 X = 2. 5 44

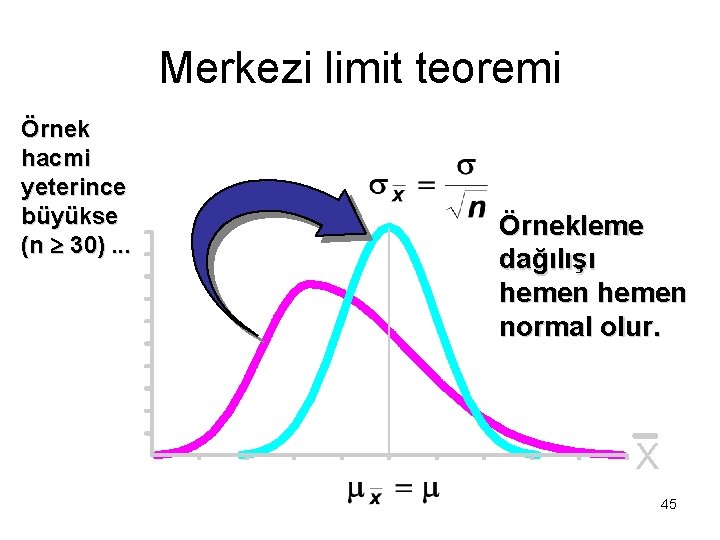
Merkezi limit teoremi Örnek hacmi yeterince büyükse (n 30). . . Örnekleme dağılışı hemen normal olur. 45

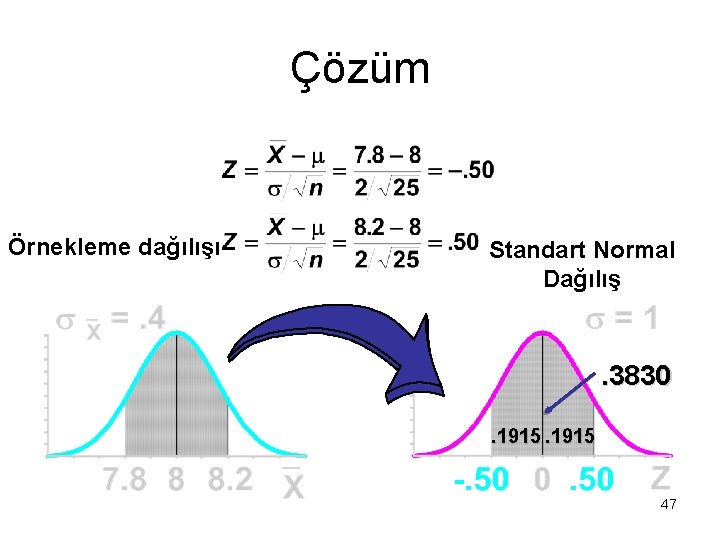
ÖRNEK 3 • Telekom’da çalışan bir uzman, uzun zaman yaptığı gözlemlerden, telefon konuşma sürelerinin (x), = 8 dk. & = 2 dk. olan normal dağılış gösterdiğini belirlemiştir. 25 görüşme rasgele seçilirse, örnek ortalamasının 7. 8 & 8. 2 dakika arasında çıkması olasılığı nedir? © 1984 -1994 T/Maker Co. 46

Çözüm Örnekleme dağılışı Standart Normal Dağılış . 3830. 1915 47

48

49

50

DAĞILIMIN TİPİ • Merkezi limit teoremine göre örnek oranının dağılımı eğer n örnek hacmi yeterince büyük ise yaklaşık olarak normal dağılıma sahiptir. • Bunun temel sebebi örnek oranının, n adet denemede ortaya çıkan ortalama başarı sayısını temsil etmesidir. • Normal dağılımın parametreleri: – Anakütle ortalaması – Anakütle varyansı 51

Dağılımın Parametreleri: Örnek Oranı için Anakütle Ortalaması 52

Dağılımın Parametreleri: Örnek oranı için Anakütle Varyansı 53

54

Örnek Oranının Standartlaştırılması 55

Örnek Hacminin Örnek Oranı Üzerindeki Etkisi 56

ÖRNEK 4 57

ÖRNEK 4 58

ÖRNEK 4 59

ÖRNEK 5 60

ÖRNEK 5 61

ÖRNEK 5 62

Ki-Kare Dağılışı = (n - 1) s 2 2 n = örnek miktarı s 2 = örnek varyansı 2 = anakütle varyansı df = serbestlik derecesi = n – 1=v 63

Ki-Kare Dağılışı 64

Ki-Kare Dağılışı 65

Ki-Kare Dağılışı 66

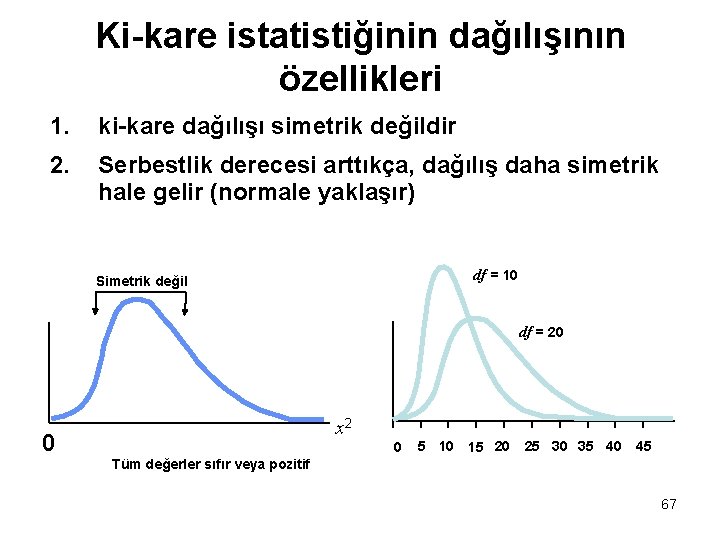
Ki-kare istatistiğinin dağılışının özellikleri 1. ki-kare dağılışı simetrik değildir 2. Serbestlik derecesi arttıkça, dağılış daha simetrik hale gelir (normale yaklaşır) df = 10 Simetrik değil df = 20 0 x 2 0 5 10 15 20 25 30 35 40 45 Tüm değerler sıfır veya pozitif 67

ÖRNEK VARYANSININ ÖRNEKLEME DAĞILIMI 68

ÖRNEK VARYANSININ ÖRNEKLEME DAĞILIMI 69

ÖRNEK VARYANSININ ÖRNEKLEME DAĞILIMI 70

ÖRNEK VARYANSININ ÖRNEKLEME DAĞILIMI 71