RNA Secondary Structure What is RNA Definition of

RNA Secondary Structure What is RNA? Definition of RNA secondary Structure RNA molecule evolution Algorithms for base pair maximisation Chomsky’s Linguistic Hierarchy Stochastic Context Free Grammars & Evolution Miscelaneous topics

Base Pairing From Przytycka

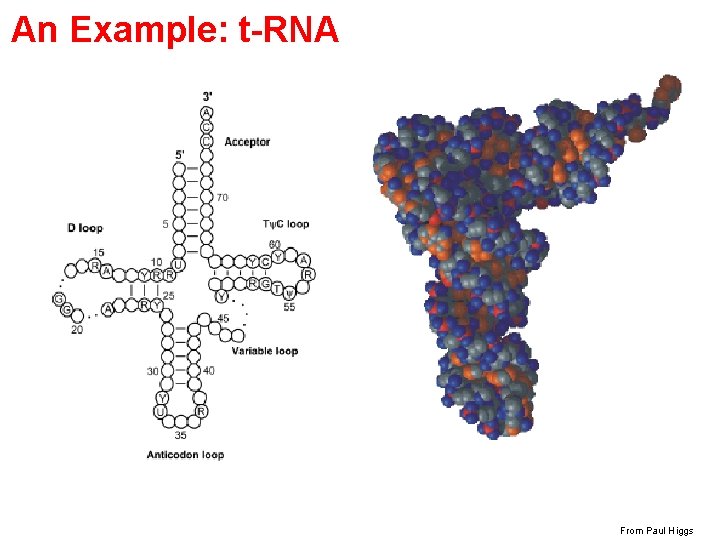
An Example: t-RNA From Paul Higgs

Known RNAs t-RNA (transfer-) m-RNA (messenger-) mi-RNA (micro-) Sn-RNA (small nuclear) RNA-I (interfering) Srp-RNA (Signal Recognition Particle) 5 S RNA 16 S RNA 23 S RNA viruses: Retroviruses (HIV), Coronavirus (SARS), . ….

Functions of RNAs Information Transfer: m. RNA Codon -> Amino Acid adapter: Other base pairing functions: Enzymatic Reactions: Structural: Metabolic: ? ? ? Regulatory: RNAi t. RNA ? ? ?

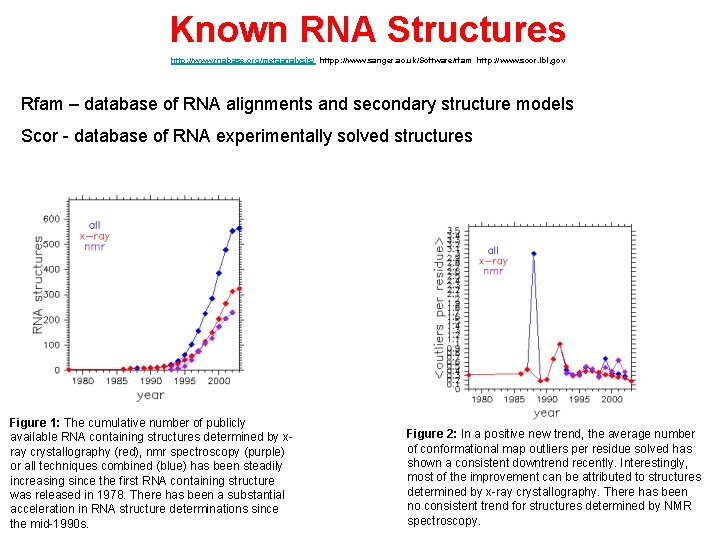
Known RNA Structures http: //www. rnabase. org/metaanalysis/ httpp: //www. sanger. ac. uk/Software/rfam http: //www. scor. lbl, gov Rfam – database of RNA alignments and secondary structure models Scor - database of RNA experimentally solved structures Figure 1: The cumulative number of publicly available RNA containing structures determined by xray crystallography (red), nmr spectroscopy (purple) or all techniques combined (blue) has been steadily increasing since the first RNA containing structure was released in 1978. There has been a substantial acceleration in RNA structure determinations since the mid-1990 s. Figure 2: In a positive new trend, the average number of conformational map outliers per residue solved has shown a consistent downtrend recently. Interestingly, most of the improvement can be attributed to structures determined by x-ray crystallography. There has been no consistent trend for structures determined by NMR spectroscopy.

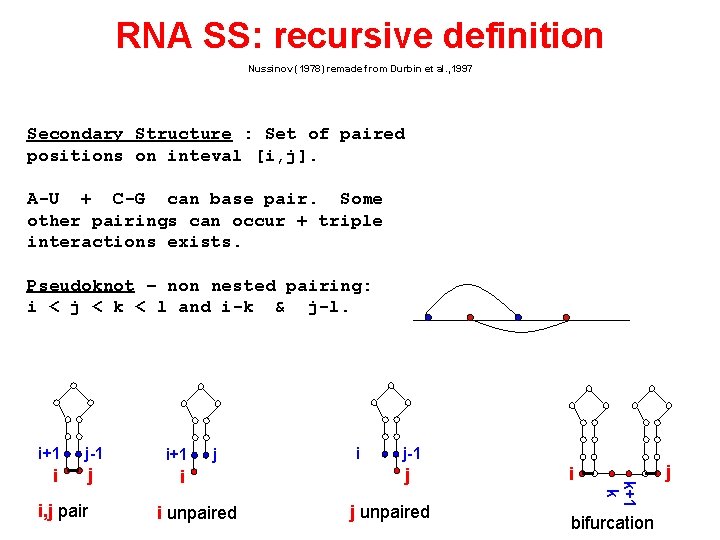
RNA SS: recursive definition Nussinov (1978) remade from Durbin et al. , 1997 Secondary Structure : Set of paired positions on inteval [i, j]. A-U + C-G can base pair. Some other pairings can occur + triple interactions exists. Pseudoknot – non nested pairing: i < j < k < l and i-k & j-l. i+1 j i, j pair i+1 j i i unpaired i j-1 j j unpaired i k+1 k i j-1 bifurcation j

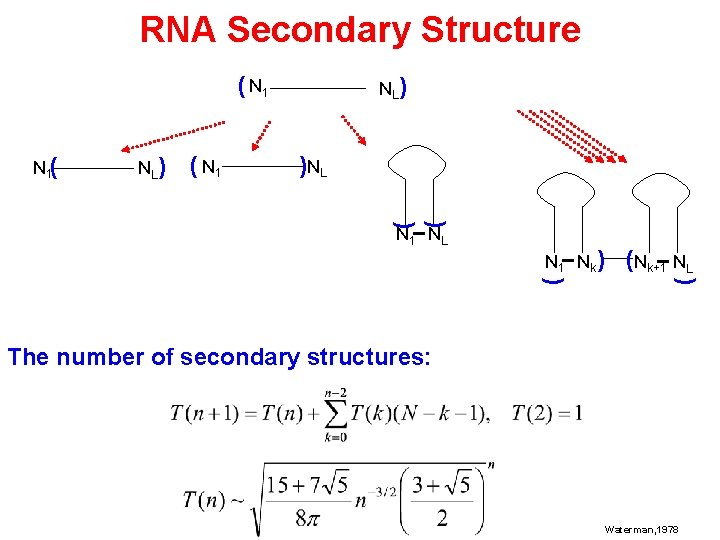
RNA Secondary Structure ( N 1( NL ) ( N 1 NL ) ) N 1 NL N 1 Nk ) (Nk+1 NL ) ) The number of secondary structures: Waterman, 1978

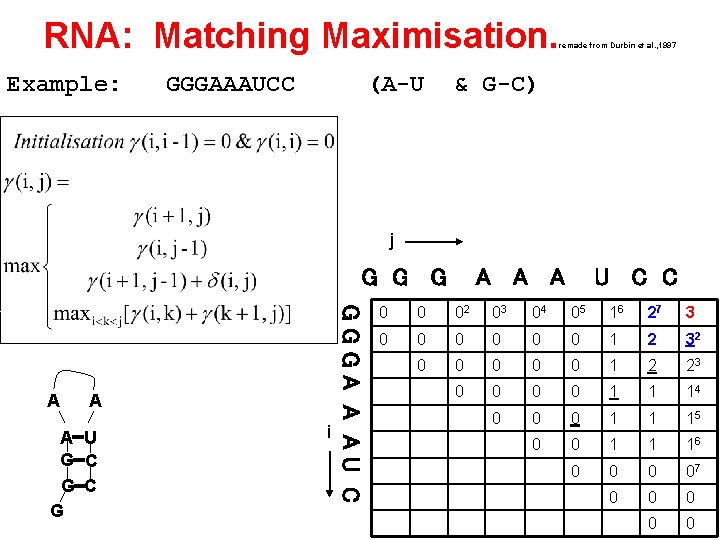
RNA: Matching Maximisation. Example: GGGAAAUCC (A-U remade from Durbin et al. , 1997 & G-C) j G G G A A U G C G i GGGA A AU C A A U C C 0 0 02 03 04 05 16 27 3 0 0 0 1 2 32 0 0 0 1 2 23 0 0 1 1 14 0 0 0 1 1 15 0 0 1 1 16 0 07 0 0 0

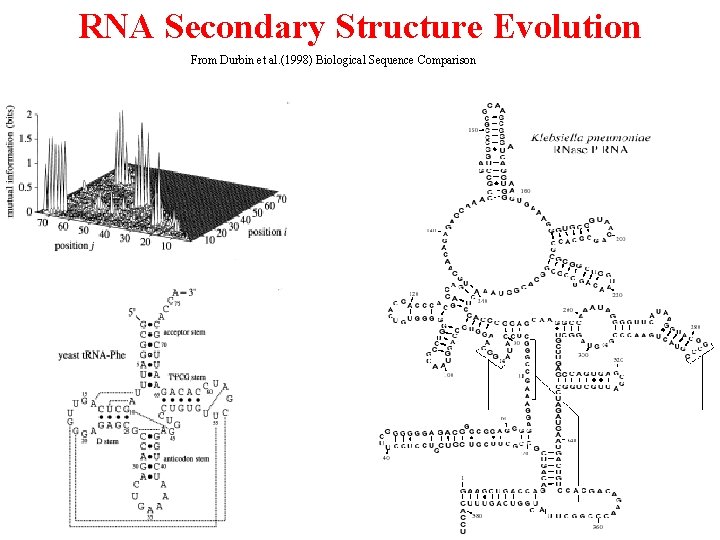
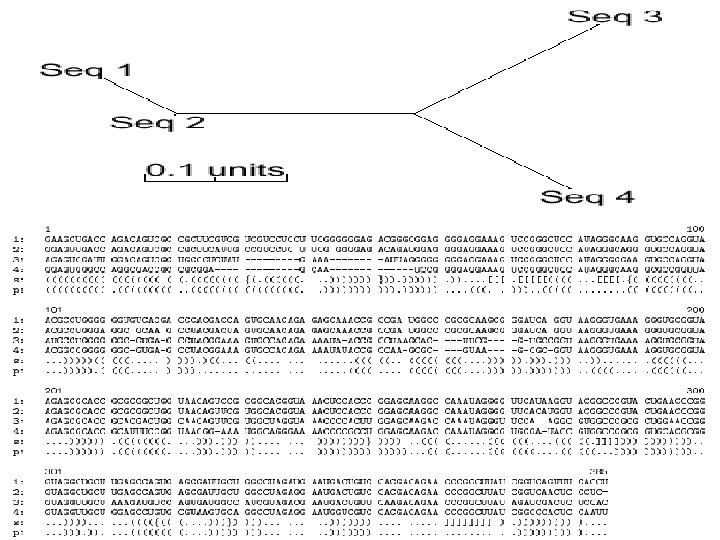
RNA Secondary Structure Evolution From Durbin et al. (1998) Biological Sequence Comparison

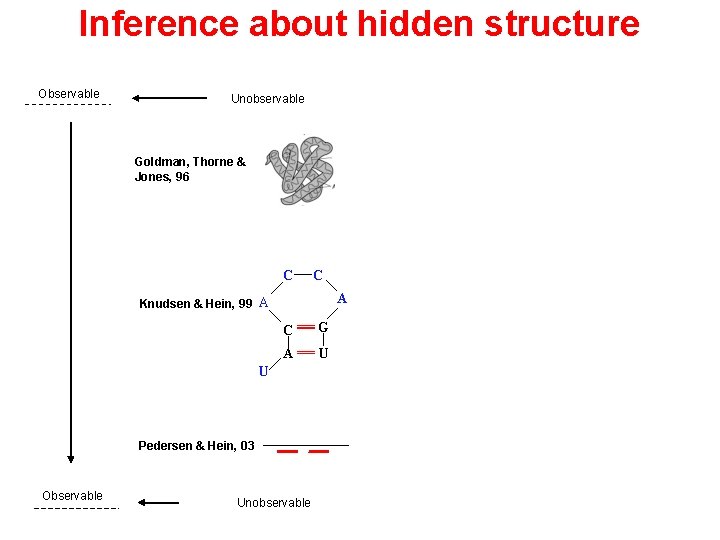
Inference about hidden structure Observable Unobservable Goldman, Thorne & Jones, 96 C C A Knudsen & Hein, 99 A C G A U U Pedersen & Hein, 03 Observable Unobservable

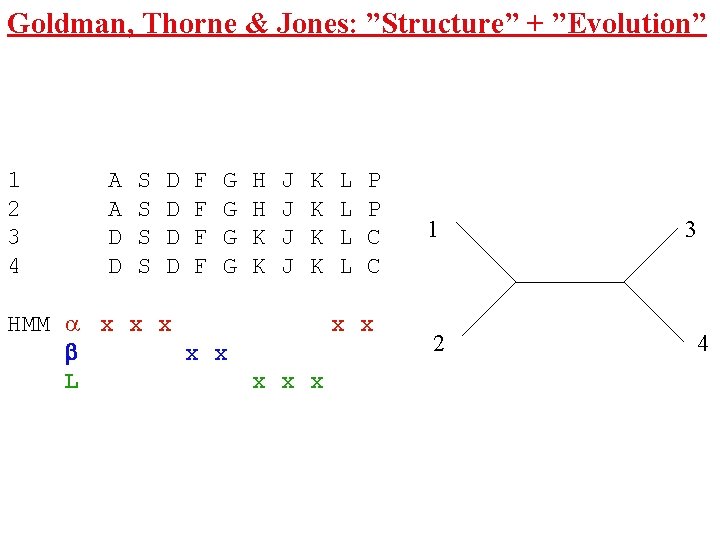
Goldman, Thorne & Jones: ”Structure” + ”Evolution” 1 2 3 4 A A D D S S D D F F G G HMM x x x x x L H H K K J J K K L L P P C C x x x 1 2 3 4

Three Questions What is the probability of the data? What is the most probable ”hidden” configuration? What is the probability of specific ”hidden” state? Training: Given a set of instances, find parameters making them probable if they were independent. O 1 H 2 H 3 O 2 O 3 O 4 O 5 O 6 O 7 O 8 O 9 O 10

The Basic Calculations What is the most probable ”hidden” configuration? O 1 O 2 O 3 O 4 O 5 O 6 O 7 O 8 O 9 O 10 H 1 H 2 H 3 What is the probability of specific ”hidden” state? O 1 O 2 O 3 O 4 O 5 O 6 O 7 O 8 O 9 O 10 H 1 H 2 H 3 The time required for these calculations is proportional to K 2*L, where K is the number of hidden states and L the length of the sequence.

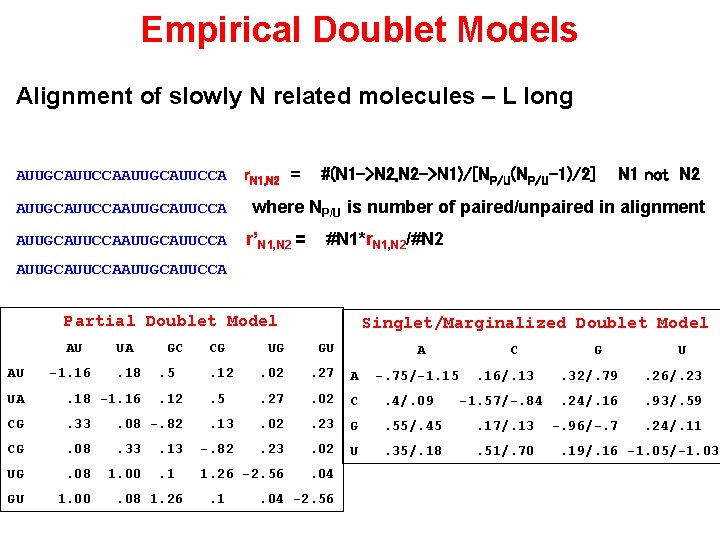
Empirical Doublet Models Alignment of slowly N related molecules – L long AUUGCAUUCCAAUUGCAUUCCA r. N 1, N 2 = #(N 1 ->N 2, N 2 ->N 1)/[NP/U(NP/U-1)/2] N 1 not N 2 where NP/U is number of paired/unpaired in alignment r’N 1, N 2 = #N 1*r. N 1, N 2/#N 2 AUUGCAUUCCA Partial Doublet Model AU AU UA -1. 16 . 18 GC CG Singlet/Marginalized Doublet Model UG GU A C . 5 . 12 . 02 . 27 A . 12 . 5 . 27 . 02 C . 4/. 09 . 13 . 02 . 23 G . 55/. 45 . 17/. 13 -. 82 . 23 . 02 U . 35/. 18 . 51/. 70 . 1 1. 26 -2. 56 . 04 UA . 18 -1. 16 CG . 33 . 08 -. 82 CG . 08 . 33 UG . 08 1. 00 GU 1. 00 . 08 1. 26 . 1 . 04 -2. 56 -. 75/-1. 15 . 16/. 13 -1. 57/-. 84 G U . 32/. 79 . 26/. 23 . 24/. 16 . 93/. 59 -. 96/-. 7 . 24/. 11 . 19/. 16 -1. 05/-1. 03

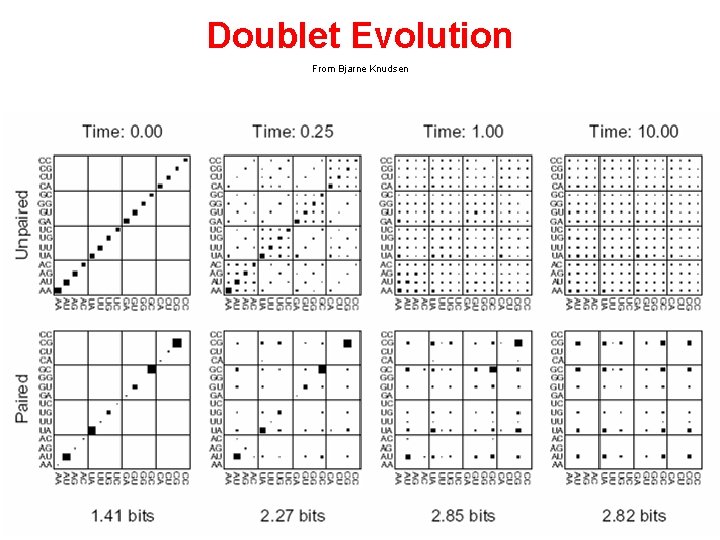
Doublet Evolution From Bjarne Knudsen

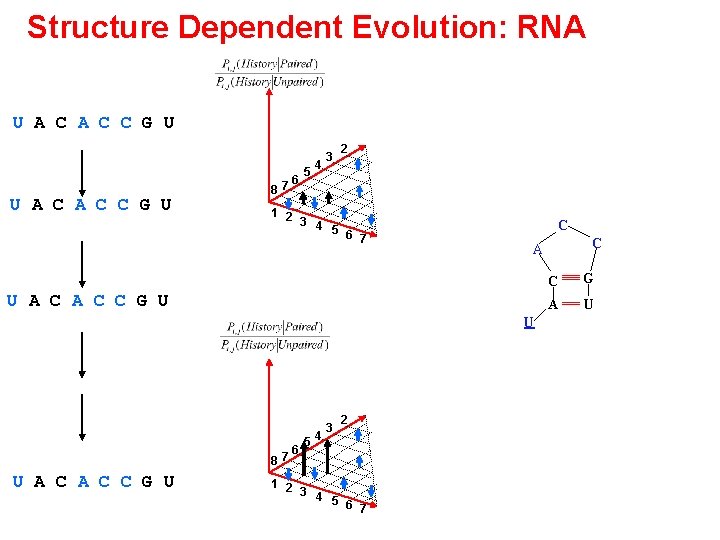
Structure Dependent Evolution: RNA U A C A C C G U 87 6 5 4 3 2 1 2 3 4 5 6 7 C U A C C G U U 87 U A C C G U 6 5 4 3 2 1 2 3 4 5 6 7 C A C G A U

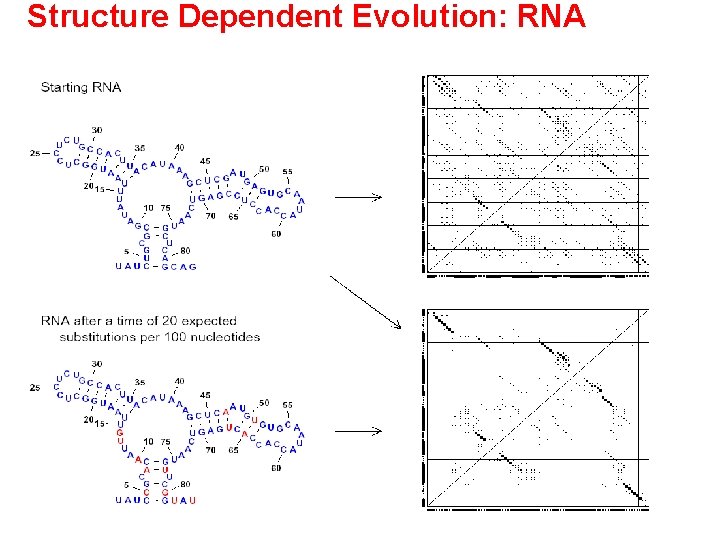
Structure Dependent Evolution: RNA

Grammars: Finite Set of Rules for Generating Strings A starting symbol: - in the present string: Context Sensitive Context Free Regular ii. A set of substitution rules applied to variables - finished – no variables General (also erasing) i.

Chomsky Linguistic Hierarchy Source: Biological Sequence Comparison W nonterminal sign, a any sign, are strings, but , not null string. Empty String Regular Grammars W --> a. W’ Context-Free Grammars Context-Sensitive Grammars Unrestricted Grammars W --> a W --> 1 W 2 --> 1 2 1 W 2 --> The above listing is in increasing power of string generation. For instance "Context-Free Grammars" can generate all sequences "Regular Grammar" can in addition to some more.

Simple String Generators Terminals (capital) --- i. Start with S Non-Terminals (small) S --> a. T T --> a. S b. T One sentence – odd # of a’s: S-> a. T -> aa. S –> aab. S -> aaba. T -> aaba ii. S--> a. Sa b. Sb aa bb One sentence (even length palindromes): S--> a. Sa --> ab. Sba --> abaaba

Stochastic Grammars The grammars above classify all string as belonging to the language or not. All variables has a finite set of substitution rules. Assigning probabilities to the use of each rule will assign probabilities to the strings in the language. If there is a 1 -1 derivation (creation) of a string, the probability of a string can be obtained as the product probability of the applied rules. i. Start with S. S --> (0. 3)a. T T --> (0. 2)a. S S *0. 3 -> a. T *0. 2 -> aa. S ii. S--> (0. 3)a. Sa S *0. 3 -> a. Sa *0. 5 -> *0. 7 –> aab. S (0. 5)b. Sb ab. Sba *0. 1 -> (0. 7)b. S (0. 4)b. T *0. 3 -> aaba. T (0. 1)aa abaaba (0. 2) *0. 2 -> aaba (0. 1)bb

Secondary Structure Generators S F L --> --> LS d. Fd s L LS d. Fd . 869. 788. 895 . 131. 212. 105

SCFG Analogue to HMM calculations (Durbin et al, 1998) What is the probability of the data? What is the most probable ”hidden” configuration? What is the probability of specific ”hidden” state? S W WL 1 i WR i’ j’ j L The time required for these calculations is proportional to K 2*L 3, where K is the number of hidden states and L the length of the sequence.

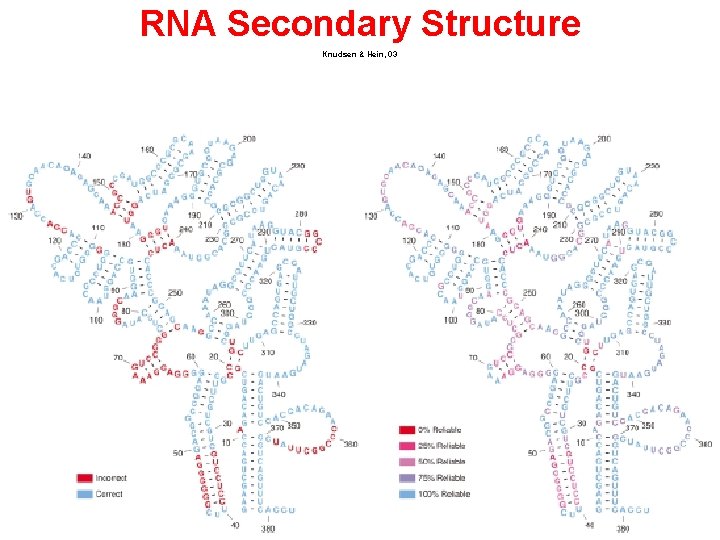
RNA Secondary Structure Knudsen & Hein, 03

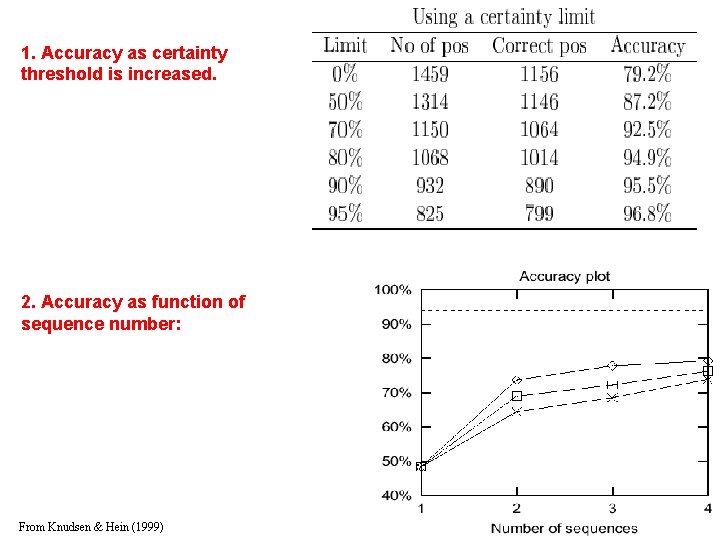
1. Accuracy as certainty threshold is increased. 2. Accuracy as function of sequence number: From Knudsen & Hein (1999)

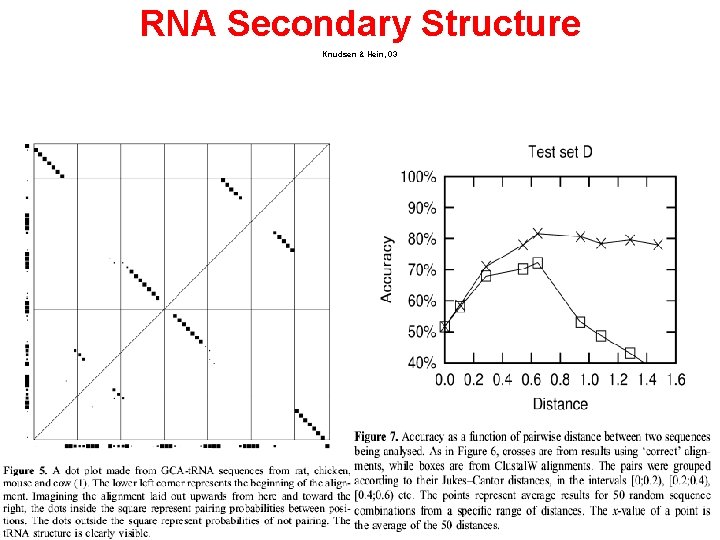
RNA Secondary Structure Knudsen & Hein, 03

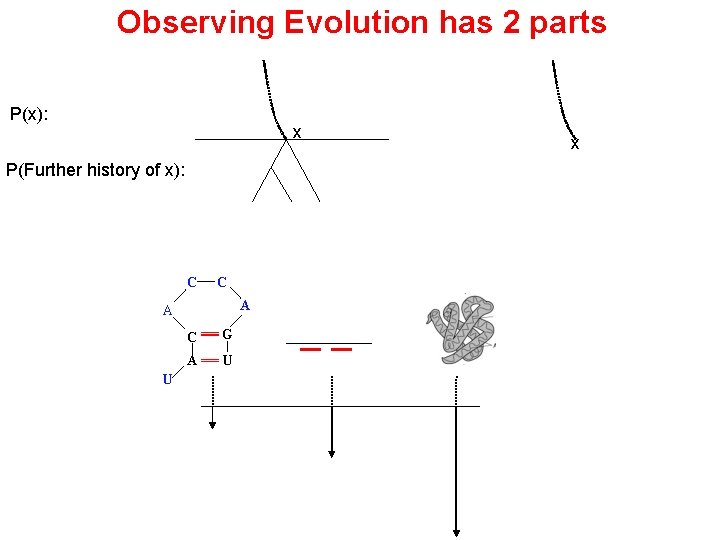
Observing Evolution has 2 parts P(x): x P(Further history of x): C C A A U C G A U x

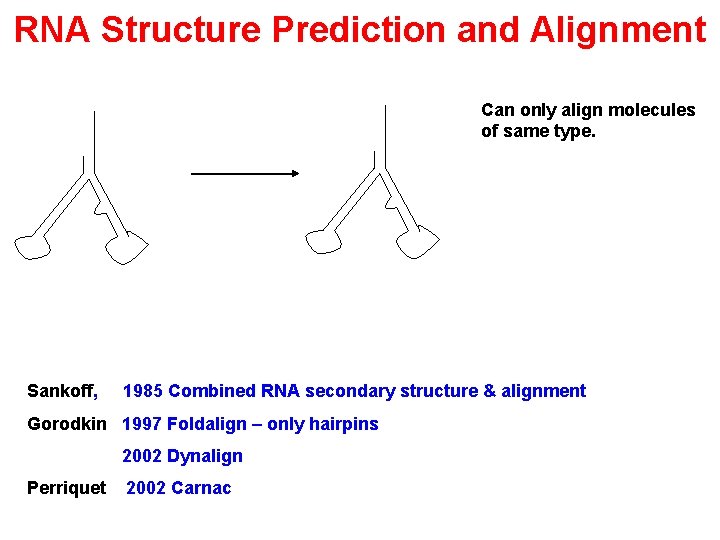
RNA Structure Prediction and Alignment Can only align molecules of same type. Sankoff, 1985 Combined RNA secondary structure & alignment Gorodkin 1997 Foldalign – only hairpins 2002 Dynalign Perriquet 2002 Carnac

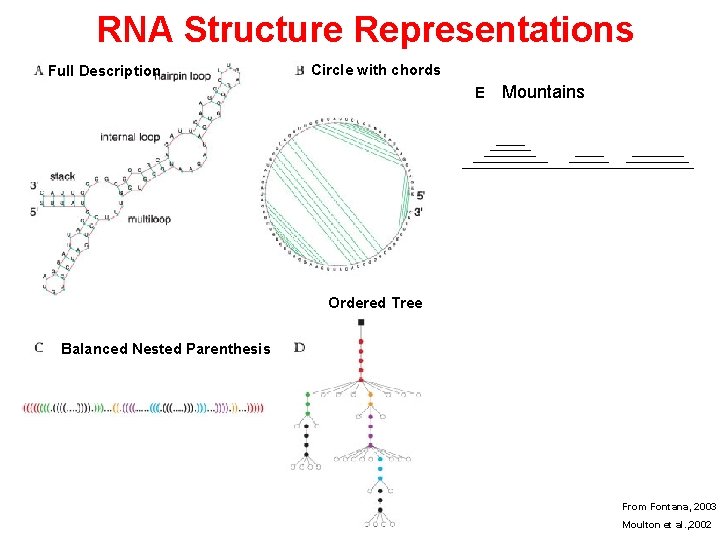
RNA Structure Representations Full Description Circle with chords E Mountains Ordered Tree Balanced Nested Parenthesis From Fontana, 2003 Moulton et al. , 2002

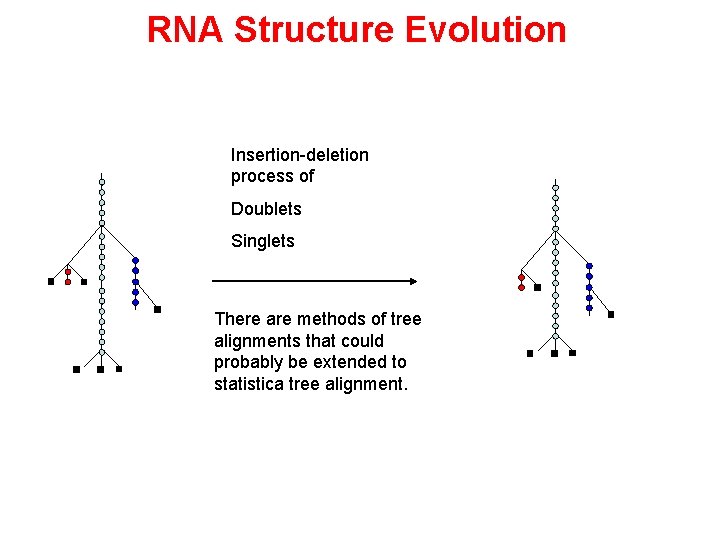
RNA Structure Evolution Insertion-deletion process of Doublets Singlets There are methods of tree alignments that could probably be extended to statistica tree alignment.

Metrics on RNA Structures Base Pair Metrics Tree Metrics Mountain Metrics Moulton, 2000

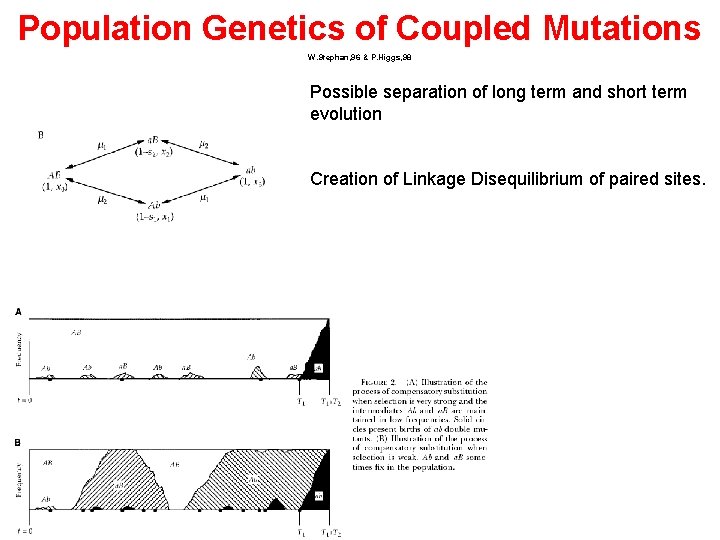
Population Genetics of Coupled Mutations W. Stephan, 96 & P. Higgs, 98 Possible separation of long term and short term evolution Creation of Linkage Disequilibrium of paired sites.

Singlet Doublet Models Kirby et al, 95, Tillier et al. , 98, Savill et al. , 01 Jukes-Cantor with bias toward base pairing: 1/4 ml, 1 difference, pairing gained 1/4 m, 1 difference, pairing unchanged 1/4 m/l, 1 difference pairing lost 0, 2 differences Ri, j=

Contagious Dependencies: Overlapping Reading Frames & CG frequencies Pedersen & Jensen, 01 n n n

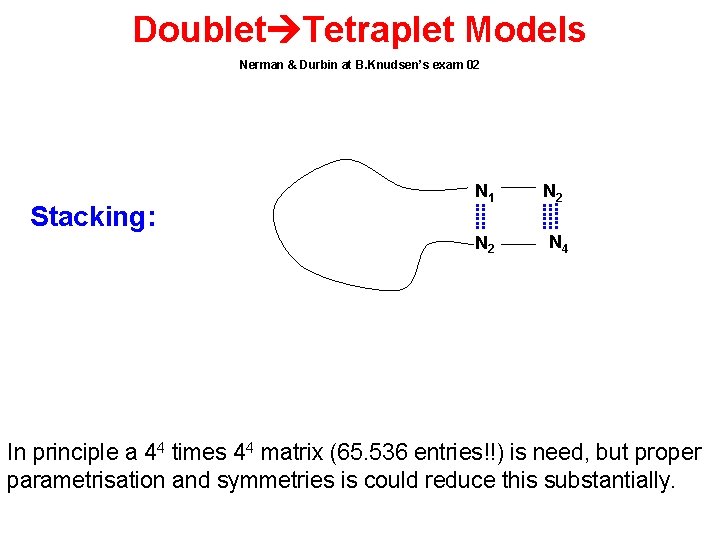
Doublet Tetraplet Models Nerman & Durbin at B. Knudsen’s exam 02 Stacking: N 1 N 2 N 4 In principle a 44 times 44 matrix (65. 536 entries!!) is need, but proper parametrisation and symmetries is could reduce this substantially.

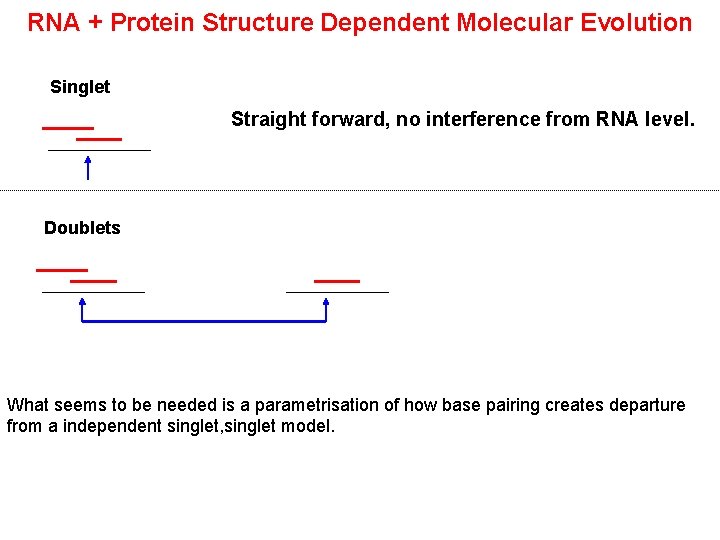
RNA + Protein Structure Dependent Molecular Evolution Singlet Straight forward, no interference from RNA level. Doublets What seems to be needed is a parametrisation of how base pairing creates departure from a independent singlet, singlet model.

Miscellaneous Topics RNA Folding Molecular Dynamics of RNA Structures RNA Structure – Sequence Landscapes RNA Homology Modelling & Threading RNA Gene Finding Close to Optimal Structures Constraint Satisfaction Modelling

Literature & www-sites Eddy, S. Non-coding RNA genes and the modern RNA world. Nat Rev Genet. 2001 Dec; 2(12): 919 -29. Review. Eddy, S. “Computational genomics of noncoding RNA genes” Cell. 2002 Apr 19; 109(2): 137 -40. Review. Fontana (2002) Modelling “evo-devo” with RNA Bio. Essays 24. 12. 1164 -77 Knudsen, B. and J. J. Hein (2003) "Practical RNA Folding” (In Press, RNA) Knudsen, B. and J. J. Hein (1999) "Using stochastic context free grammars and molecular evolution to predict RNA secondary structure (Bioinformatics vol 15. 5 15. 6. 446 -454) Moore (1999) Structural Motifs in RNA Ann. Rev. Biochem. 68. 287 -300. Moulton et al. (2000) Metrics on RNA Secondary Structures J. Compu. Biol. 7. 1/2. 277 Perriquet et al. (2003) Finding the common homologous structure shared by two homologous RNAs. Bioinformatics 19. 1. 108 -116. http: //www. imb-jena. de/RNA. html http: //scor. lbl. gov/index. html http: //www. rnabase. org/metaanalysis/