RLC Circuits Network Analysis with Differential Equations Afzal

RLC Circuits Network Analysis with Differential Equations Afzal Hossain and Eric Tung

Quick Layman’s Explanation. Charge � An ‘amount’ of electrons (approximately 6. 241× 1018 of them). Current � The flow of charge/electrons over time, caused by a voltage. � Can be thought of as the derivative of charge. Voltage � Potential Electric Energy. � Essentially the work a ton of electrons stuck in a battery/power source can do. � When the battery is connected to ‘ground’, or something with less electrons, a current forms as the electrons rush out of the battery. � The electrons then release their energy to any components passed on the wire. � So basically, the difference in the amount of electrons between two different points in a circuit.

Resistors �Basically connecting a wire directly to ground causes a huge current, akin to a ‘stampede’ of charges. �This causes fires and bad things. We don’t like bad things. Like the dark, or the closet. �Resistors slow down the flow of current, ‘resisting’ it. �Dissipates extra energy as heat. � Voltage from the battery causes current. � We are limiting current. � That excess voltage has to go somewhere. �So the relationship between voltage, current, and resistance is:

Capacitors � Basically two unconnected plates that are extremely close to each other. � Takes advantage of this ‘stampede’ effect. � The plates are so close, that initially it behaves as a direct short to ground. No voltage on the capacitor initially. � Electrons/current flow comes rushing in, gets trapped. � Electrons build up in the capacitors, which causes a voltage to form over the capacitor. � This happens because we have a ton of electrons stuck on one plate of the capacitor, and little to none on the other, just like they were stuck in the battery. � This voltage over the capacitor (buildup of electrons) repels any new electrons coming in. Current flow slows to a halt. � The bigger the capacitor voltage, which changes over time, the less current into the capacitor. So the formula here is:

Inductors � Is a very tightly wound coil of wire. � Behaves like a ‘traffic jam’. � Electrons rush to the inductor when the circuit is connected to ground. � The inductor blocks the current by producing a magnetic field that resists the flow of electrons. � Basically electrons are stuck on one side of the inductor, ala a traffic jam, causing a voltage over the inductor. � Eventually all the electrons get through. The flow of current rises, the blockage slowly clears away, and thus the inductor voltage disappears. � So the voltage depends on how fast the blockage can clear, or how fast the current can start to flow at a normal rate again. So, the formula here is:

Series RLC Circuits. � So in a series circuit, you have a power source, connected to a Resistor, to a Capacitor, to an Inductor, and back to the power source, in a single loop. � The voltages over each component, added up, are equal to the power supply’s voltage. � The current through each component is the same, as there’s only one path the current can take. � The basic current and voltage formulas are listed on the right.

� So we have the formulas: �We need to rearrange the last formula to give voltage, not current. � We simply divide both sides by C, then integrate with respect to t. Derivation of the Characteristic Equation Miscellaneous Notes • The integral of I is Q, since Q is charge and I is the flow of charge over time. • We leave the integral in the formula since we’ll be taking the derivative of the equation soon. • Essentially, if we keep taking derivatives, it goes: � Thus, Kirchoff’s voltage law goes from this: Q -> Q’’’ • Which is the same as: � To this: Q -> I’’

Derivation of the Characteristic Equation, Cont. � Integrals are a pain to deal with, so we differentiate the entire equation to get: � Note that since IL = IR = IC, we’re dealing with one current that we just call I. � Also note that if we have a: � DC voltage source (Constant Voltage), when we differentiate, we get 0 for VS(t), which means we’ll get a homogenous solution only. � AC voltage (Sinusoidal Voltage), when we differentiate, we’ll get some sin(t) or cos(t) function back. We’ll then have to solve for a homogenous and particular solution.

A Simple Series Circuit Problem � Given a First-Order RL circuit with the following parameters: � E = 50 sin(t) Volts � I(0) = 0. � We start with the standard series equation and fill in the parameters:

� Take the Laplace Transform of both sides: Solving the RL circuit (The equation was divided by 2 in the first step. ) � Perform a Partial Fraction Decomposition: I(0) = 0, so the initial condition disappears from the equation.

� By comparing terms, we get the following linear equations: Solving the Partial Fraction Decomposition � We throw the equations into a matrix and The numbers for � Our partial fractions so far look like this: So, a matrix was used. solve. this particular problem weren’t so easy to compute with the standard methods.

� Lastly, we take the Inverse Transform: � We can calculate the wave’s magnitude and phase using the following formula: Where: � Magnitude(C) � Angle Determining Magnitude and Phase As we can see, we have: • transient (exponential) • steady-state (trigonometric) • parts to the � So the waveform looks like: � We can see the graph of the equation and it’s parameters on the next page. solution, which was expected.

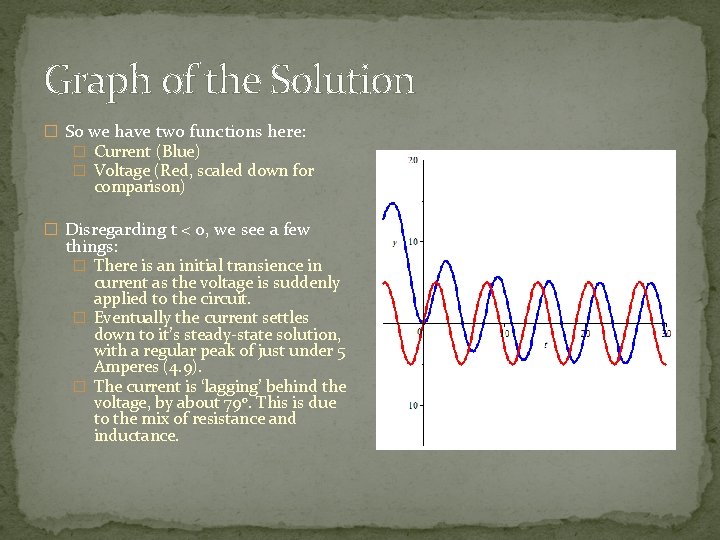
Graph of the Solution � So we have two functions here: � Current (Blue) � Voltage (Red, scaled down for comparison) � Disregarding t < 0, we see a few things: � There is an initial transience in current as the voltage is suddenly applied to the circuit. � Eventually the current settles down to it’s steady-state solution, with a regular peak of just under 5 Amperes (4. 9). � The current is ‘lagging’ behind the voltage, by about 79 o. This is due to the mix of resistance and inductance.

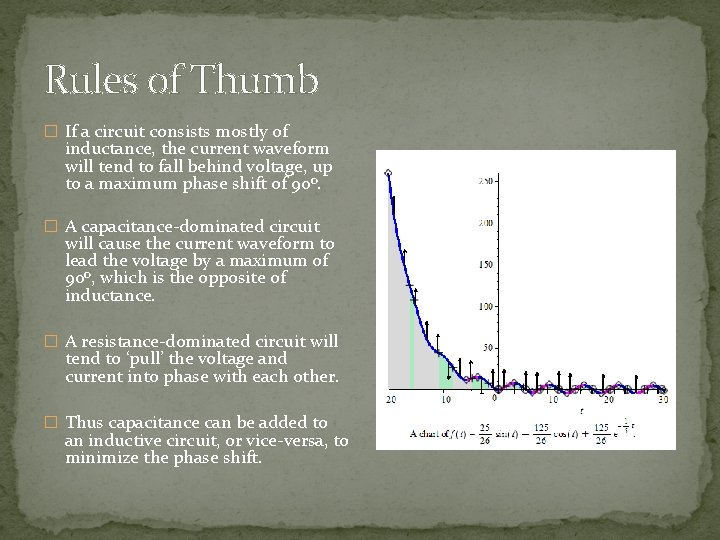
Rules of Thumb � If a circuit consists mostly of inductance, the current waveform will tend to fall behind voltage, up to a maximum phase shift of 90 o. � A capacitance-dominated circuit will cause the current waveform to lead the voltage by a maximum of 90 o, which is the opposite of inductance. � A resistance-dominated circuit will tend to ‘pull’ the voltage and current into phase with each other. � Thus capacitance can be added to an inductive circuit, or vice-versa, to minimize the phase shift.

Parallel RLC Circuits. � The parallel RLC circuit has the exact opposite properties as the series circuit. � The parallel circuit will have dedicated branches for each component in the circuit. � Electrons now have an option of which branch to take through the circuit, so the current though each branch will add up to the total current from the battery. � The electrons will naturally distribute themselves so that the voltage across each branch is the same.

Parallel Circuit Derivations � Let’s start with substituting into the equation for current. � VR = VC, so instead of VR/R, we put VC/R. � We also know that a capacitor’s voltage depends on the change in current with respect to time. � Let’s set up the equation for voltage now. We know V L equals the inductance times the derivative of the current. Let’s now take the derivative of that: � Now we have formulas that allow us to switch between current and voltage and back.

Parallel Voltage and Current Relations �Let’s make a table so that we can easily substitute between voltage and current. Inductor Current Capacitor Voltage

�Now we just substitute in current for voltage and simplify for an equation in I L. Characteristic Equations for Parallel VR = VC, so VR/R = VC/R. �Likewise, we can substitute the other way and get a second-order equation in terms of VC: We just use VC where possible.

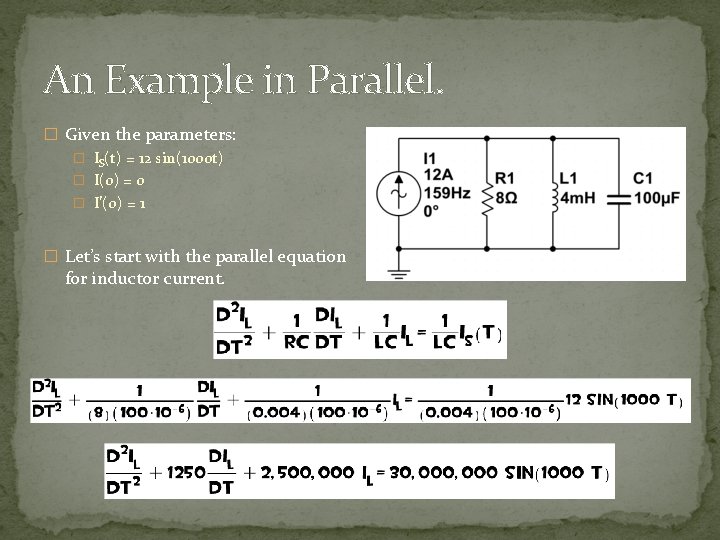
An Example in Parallel. � Given the parameters: � IS(t) = 12 sin(1000 t) � I(0) = 0 � I’(0) = 1 � Let’s start with the parallel equation for inductor current.

Parallel characteristic Equations. �Now, let’s fill out the equation for voltage. �For the sake of brevity, we’ll let Maple handle the following steps.

Maple Commands and Calculations I suppose I should’ve chosen a circuit with easier numbers to calculate; But that would be ignoring the fact that real, practical circuits would operate at such high frequencies.

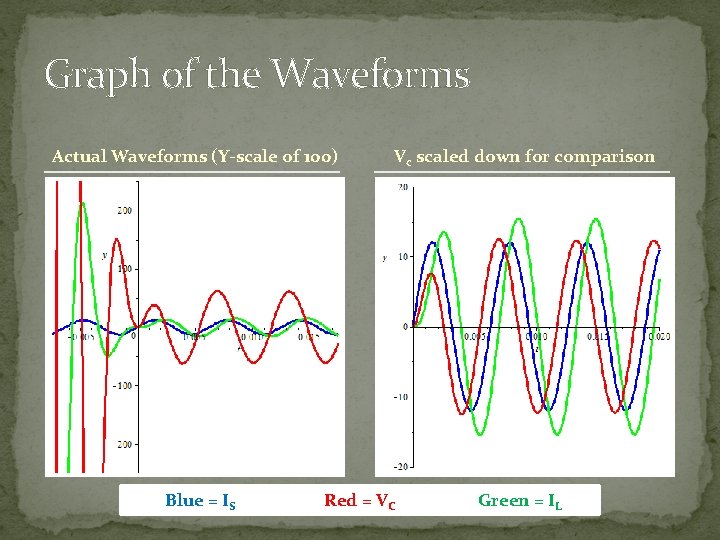
Graph of the Waveforms Actual Waveforms (Y-scale of 100) Vc scaled down for comparison Blue = IS Green = IL Red = VC

�Using the magnitude and phase equations that were covered in the series example, we get the waveforms: Parallel Results and Analysis. VC = VS = VL = VR in this circuit, actually. �A few remarks: � As can be seen, Is leads Vc by 50. 19 o. � Because this is a parallel circuit, Vc just so happens to be equal to Vs. � If Vc = Vs, then we can see IL lagging behind the source voltage by 42. 5 o. The results do seem to confirm our knowledge of the behavior of capacitors and inductors.

Series-Parallel, and Advanced Circuitry � In the next few sections, we will take a look at advanced circuit-analysis techniques that deal with circuits not purely connected in series or parallel. � Although there’s going to be a jumble of math onwards form here (you’ve been forwarned), there is always one thing you should be looking for: � If you have only a RC or RL network, then you get a first- order equation. Easy to solve. � If we’re dealing with a RLC circuit, we try to find as many (Inductor) current and (Capactitor) Voltage relationships as we possibly can, then substitute in for a differential equation entirely in ILn or VCn. � (Where ‘n’ is the inductor or capacitor component that will be your reference point in the circuit).

Basic First-Order Mesh Analysis � Mesh analysis consists of breaking up a circuit into multiple loop-currents, then writing equations based on � The components that the loop-current goes through. � The relationships that the selected loop-current has with other loop-currents in the circuit. � This will result in a system of equations. The system will be as big as the number of loops involved.

Creating loop 1: � We’ll now write an equation for this loop (boxed and highlighted), with some assumptions: � In all loops, we are going � � clockwise (As denoted by the highlighted arrow). The sign on the voltage source will be negative, as we are approaching the source from it’s negative terminal. All other components will be associated with a positive sign. If we went around the loop counterclockwise, all the signs would be negated. All the voltages within this loop will add up to a net total of zero. � We’ll start at V 2. Ready? Go!

� Now that we have a mesh equation, we can start substituting in for the resistors and inductors. � You might be asking at this point, “Where did I 2 come from”? � Well, on the diagram, you can see that I 2 (the grey arrow) is flowing in the opposite direction of I 1 (orange arrow). � Although we’re only focusing on I 1, I 2 will still affect the circuit, so we need to account for that. � We can think of I 2 as “opposing” I 1, so we take the difference of both currents. � If ever there was a situation where two currents were flowing in the same direction, we would add the currents together. � So now that we’ve created a mesh equation in terms of I 1, we can do the same for loop-current I 2. � Let’s start at the component at the top, the inductor at Z 3. � Once again, we’ll go through the components clockwise. Finding the Mesh Equations In any particular loop, all the voltages must add up to zero. So V 1 + V 2… Vn = 0 Just, instead of using V, we use: I(R) for resistors. L(d. I/dt) for inductors. Q/C for capacitors.

Creating Loop 2: � Note here that current I 2 is the main focus, so I 1 is subtracted from I 2 this time around. � Rearranging mesh eq. 2 in terms of I 1 gives us the equation on the right:

� Substitute mesh equation 2 into mesh equation 1 and simplify: Mesh Equations, Continued. Note that in the first equation, the first term was split: From: (d. I 1/dt) To: (d/dt)I 1 � This is now a second-order equation that can be solved using various methods. � So let’s do an actual example from scratch this time, as the previous examples relied on you following the derivation and theory completely. � We’ll be using the same schematic for this. Which helps, because now we can substitute in I 1.

Mesh Equation 1 � Let’s find mesh equations that are specific to this problem. � For loop 1, we’ll again start at V 2 and go around the loop clockwise. � We then move all the voltage to the other side of the equation, and substitute for the components. � Again, at R 1, we need to take note of I 2’s opposing flow.

Mesh Equation 2 � We do the same for loop 2, starting clockwise at L 2. � Now we rearrange the equation in terms of I 1:

� Using these two equations: Getting the Differential Mesh Equation So far we’re found � We substitute and simplify: the characteristic equation. Now we need to find the solution. � We can plug in the numbers directly from our derived differential equation and see that, yes, the numbers do match up.

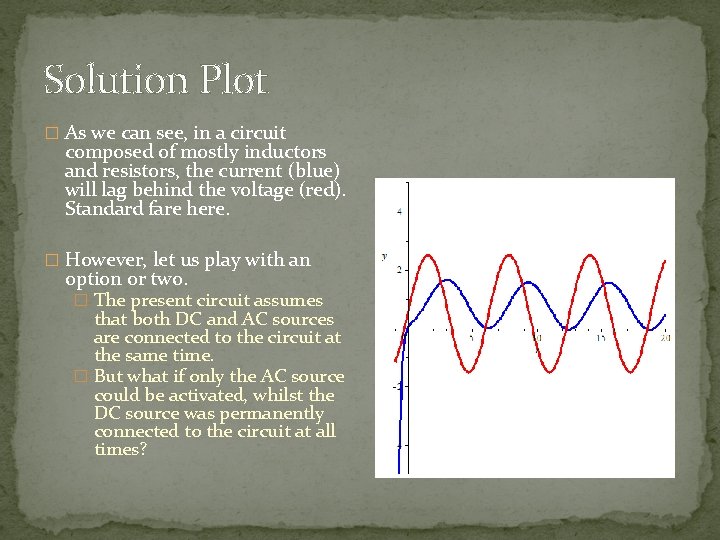
Solution Plot � As we can see, in a circuit composed of mostly inductors and resistors, the current (blue) will lag behind the voltage (red). Standard fare here. � However, let us play with an option or two. � The present circuit assumes that both DC and AC sources are connected to the circuit at the same time. � But what if only the AC source could be activated, whilst the DC source was permanently connected to the circuit at all times?

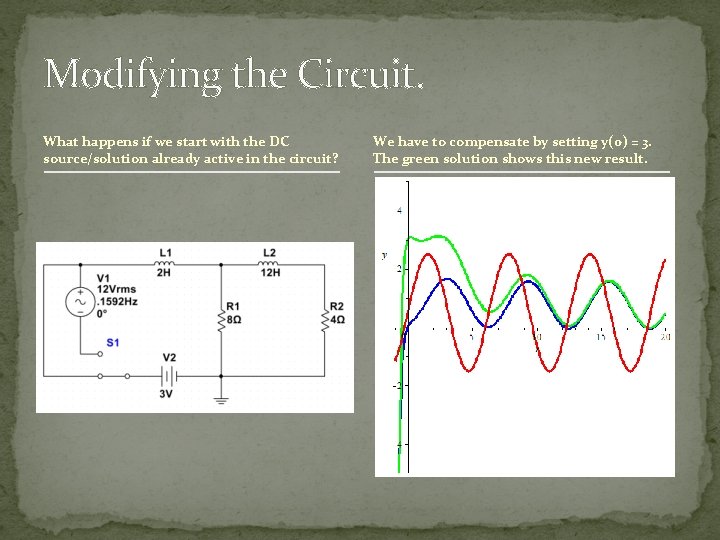
Modifying the Circuit. What happens if we start with the DC source/solution already active in the circuit? We have to compensate by setting y(0) = 3. The green solution shows this new result.

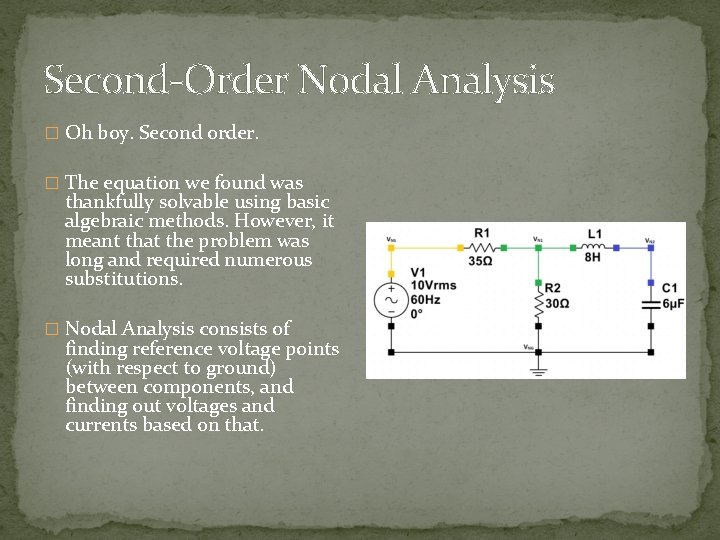
Second-Order Nodal Analysis � Oh boy. Second order. � The equation we found was thankfully solvable using basic algebraic methods. However, it meant that the problem was long and required numerous substitutions. � Nodal Analysis consists of finding reference voltage points (with respect to ground) between components, and finding out voltages and currents based on that.

� First we set up the equations for current. Setting up the Nodal Equations � We know that current going into node VN 1 In this example, we equals the current flowing out. � We also know that VN 2 is the voltage at VN 1 minus the voltage across the inductor, VL. wrote a formula in terms of VN 2, as that was probably the most relevant to this circuit. � Because VL is an inductor, VL is just the (Finding voltage over a resistor, for example, is trivial. ) change in current over time. � Let’s also rearrange a couple of formulas. Keep these 3 formulas in mind.

� From this point on, there’s going to be a lot of substitution. See if you can follow along. � We’ll substitute in the first formula into the second, then the second into the third. � Substitute equations in for IS and I 2. � At this point, we rearrange an equation in terms of VN 1. � We’ll start simplifying the equation after this next substitution. Nodal Equations, Continued. In total, there are 4 substitutions we need to make in the example.

� Substituting in and simplifying: Finding the characteristic equation. I know this is long, � We make one more substitution below, before arriving at a second-order equation that is completely in terms of VN 2. but most secondorder mesh or nodal analysis result in a huge system of differential equations in a matrix. That in itself is another semester’s worth of work.

� While we’re at it, we can find the voltage across the inductor relatively easily. � The current through the capacitor is based the changing voltage through the capacitor. � That current also flows through the inductor, by consequence of the 2 components being connected together in series. So to Recap: • We found a differential equation in terms of VN 2, which is equal to VC. • The capacitor and � Differentiating that and multiplying by L: inductor current is the derivative of VC. • We find VL by taking the derivative of VC. � This holds since voltage over an inductor depends on the derivate of it’s current. � To find the voltage VN 1, we just add: • We find VN 1 by adding the capacitor and inductor voltages.

A Quick Note on Multiple Sources. � Usually a circuit will have a phase reference at one of the voltage sources, with the other sources out of phase with respect to that source. � The phase shift can be converted using the formula to the right. In terms of the equation, you will simply have more particular solutions to crunch out.