Risk Continuum Stakeholder relations Terms of contract Location

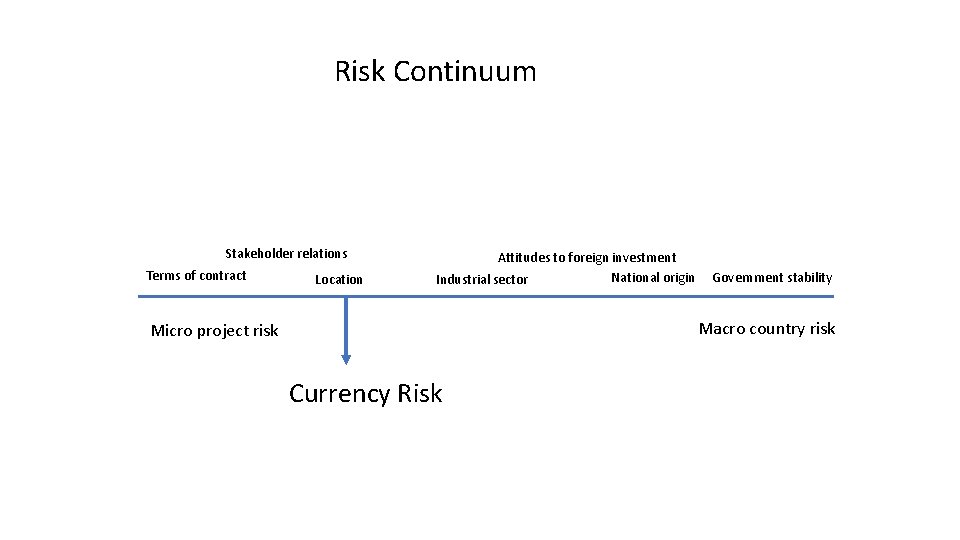
Risk Continuum Stakeholder relations Terms of contract Location Attitudes to foreign investment National origin Industrial sector Government stability Macro country risk Micro project risk Currency Risk

Evolution of the International Monetary System • Bimetallism: Before 1875 • Classical Gold Standard: 1875 -1914 • WWI • Inter-war failures • Post-war policy • Bretton Woods and the dollar standard

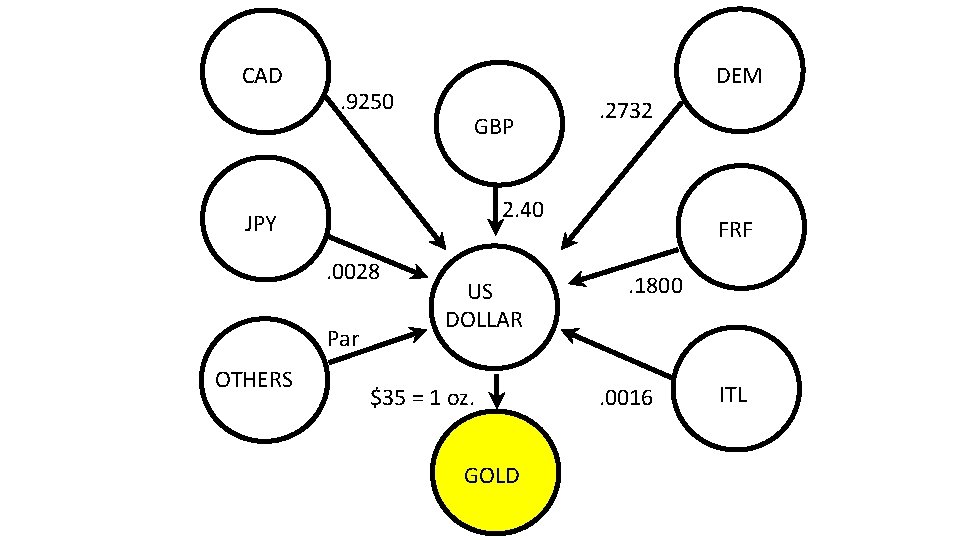
CAD . 9250 DEM GBP 2. 40 JPY. 0028 Par OTHERS . 2732 US DOLLAR $35 = 1 oz. GOLD FRF. 1800 . 0016 ITL

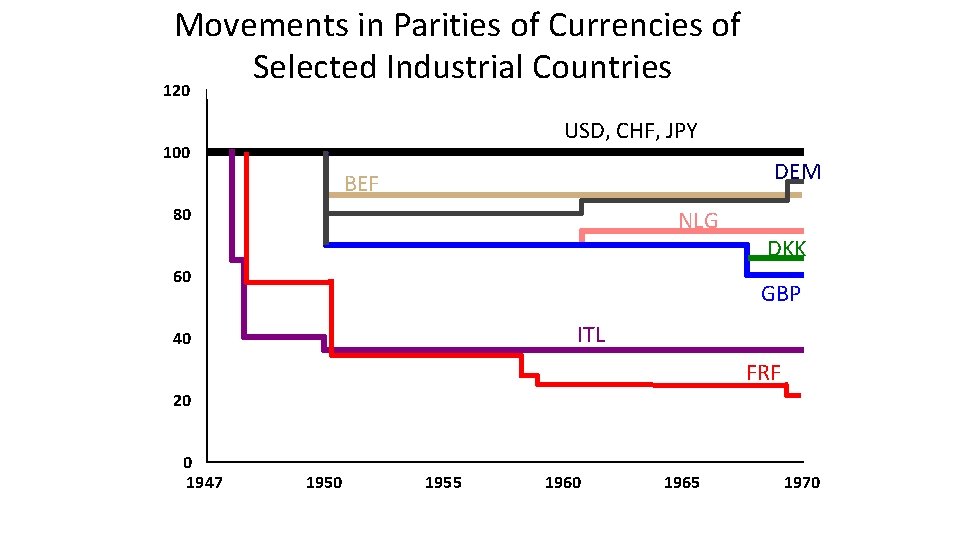
Movements in Parities of Currencies of Selected Industrial Countries 120 USD, CHF, JPY 100 DEM BEF 80 NLG 60 DKK GBP ITL 40 FRF 20 0 1947 1950 1955 1960 1965 1970

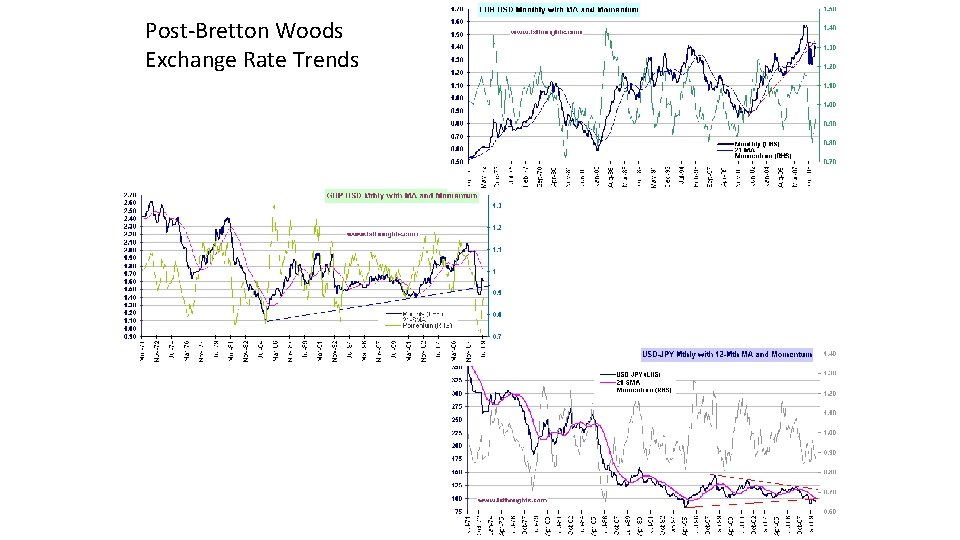
Post-Bretton Woods Exchange Rate Trends

Evolution of the International Monetary System • Bimetallism: Before 1875 • Classical Gold Standard: 1875 -1914 • WWI • Inter-war failures • Post-war policy • Bretton Woods and the dollar standard • Current situation

Hedging Currency Risk Market based methods • Exchange traded markets • Clearinghouse • Over the counter (OTC) • Long and short asset positions • Derivatives (on versus off balance sheet) • Operational hedges

Foreign Exchange: Risk Identification and Management

Foreign exchange risk policy formation • Foreign exchange risk exposures can be classified in terms of their impact on a firm’s cash flows, balance sheet, competitive position and value.

Foreign exchange risk policy formation • Transaction exposure • The risk that future foreign currency denominated cash flows will vary on account of exchange rate movements. • E. g. a contract to import goods from the US denominated in USD • Economic exposure • The effect of exchange rate movements on the ongoing business operations of a firm (i. e. the net present value of its future cash flows). • It includes both asset exposures and operating FX exposures and extends further to recognise the impact of FX risk on the value of a firm. • Translation or accounting exposure • The risk that conversion and consolidation of foreign currency assets or liabilities will impact adversely on the balance sheet. • E. g. a firm accumulates assets and liabilities overseas and at a future date translates their value onto its consolidated balance sheet

Foreign exchange risk policy formation • FX objectives • Consideration of what the company intends to achieve and how it will do so, by specifying the following: • The products and services that can be used to manage FX risk exposures; e. g. forward exchange contracts and currency swaps • The style of risk management • Active—hedging techniques continuously adjusted in response to forecast changes in the exchange rate • Defensive—a defined percentage of identified risk exposure is automatically hedged

Measuring transaction exposure • The risk faced by firms that the currency value will change between the time an order is placed and the time of its payment. • This risk is caused by uncertainty as to the exact value of the transaction. • Transaction exposure risk has two directional components 1. Downside exposure • Amount received (paid) in the future is less (more) than the current projected amount 2. Upside exposure • Amount received (paid) in the future is more (less) than the current projected amount

Risk management: market-based hedging techniques • A firm may attempt to minimise FX risk (particularly downside exposure) through the use of hedging techniques/instruments. • Hedging instruments include: • forward exchange contracts • money-market hedge • futures, options and swaps

Risk management: market-based hedging techniques • Forward exchange contracts • Lock in an exchange rate today for delivery or receipt of a foreign currency at a specified future date. • Money-market hedging to cover FX risk • Also called ‘BSI hedge’—borrow, spot, invest

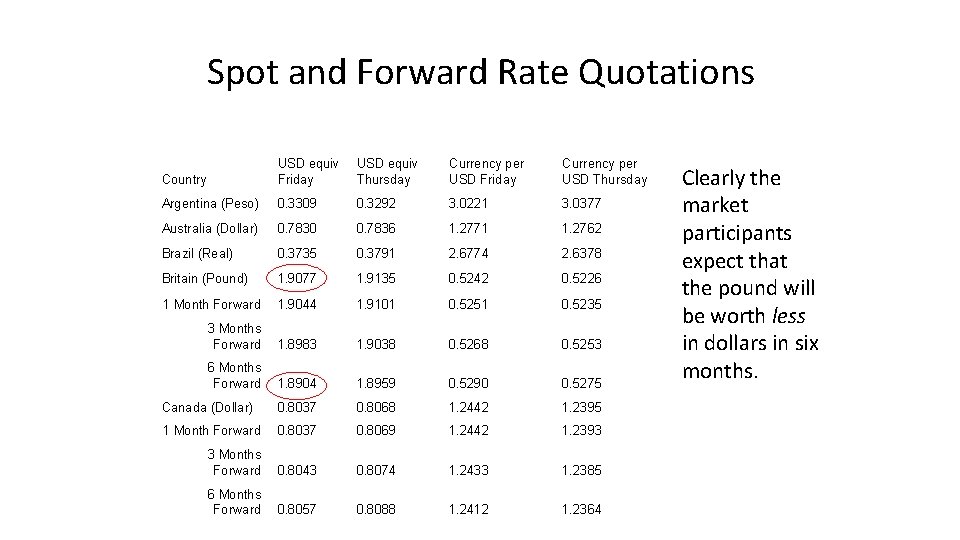
Forward Rate Quotations • The forward market for FX involves agreements to buy and sell foreign currencies in the future at prices agreed upon today. • Bank quotes for 1, 3, 6, 9, and 12 month maturities are readily available forward contracts. • Longer-term swaps are available.

Spot and Forward Rate Quotations Country USD equiv Friday USD equiv Thursday Currency per USD Friday Currency per USD Thursday Argentina (Peso) 0. 3309 0. 3292 3. 0221 3. 0377 Australia (Dollar) 0. 7830 0. 7836 1. 2771 1. 2762 Brazil (Real) 0. 3735 0. 3791 2. 6774 2. 6378 Britain (Pound) 1. 9077 1. 9135 0. 5242 0. 5226 1 Month Forward 1. 9044 1. 9101 0. 5251 0. 5235 3 Months Forward 1. 8983 1. 9038 0. 5268 0. 5253 6 Months Forward 1. 8904 1. 8959 0. 5290 0. 5275 Canada (Dollar) 0. 8037 0. 8068 1. 2442 1. 2395 1 Month Forward 0. 8037 0. 8069 1. 2442 1. 2393 3 Months Forward 0. 8043 0. 8074 1. 2433 1. 2385 6 Months Forward 0. 8057 0. 8088 1. 2412 1. 2364 Clearly the market participants expect that the pound will be worth less in dollars in six months.

Forward Market Hedge • If you are going to owe foreign currency in the future, agree to buy the foreign currency now by entering into long position in a forward contract. • If you are going to receive foreign currency in the future, agree to sell the foreign currency now by entering into short position in a forward contract.

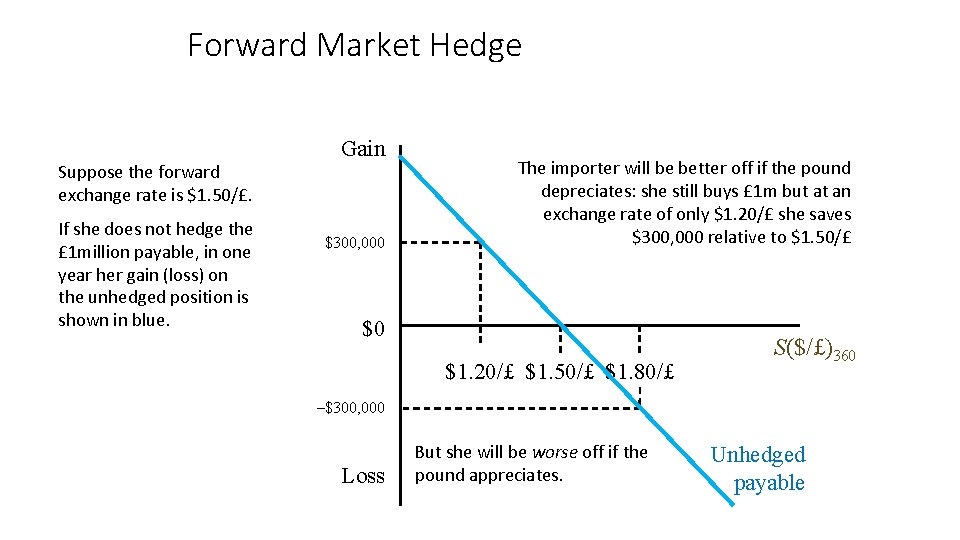
Forward Market Hedge: an Example A U. S. importer of British candles has just ordered next year’s inventory. Payment of £ 1 million is due in one year. Question: How can she fix the cash outflow in dollars?

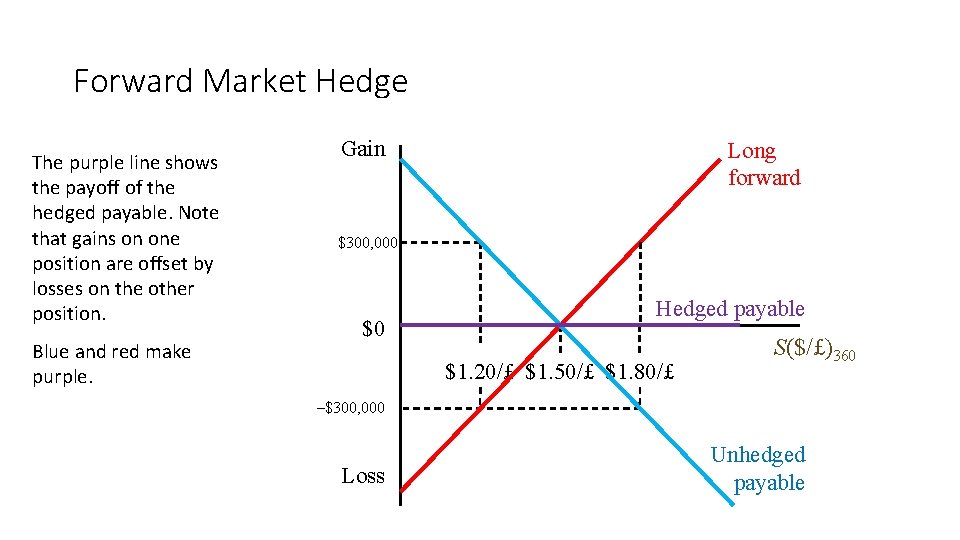
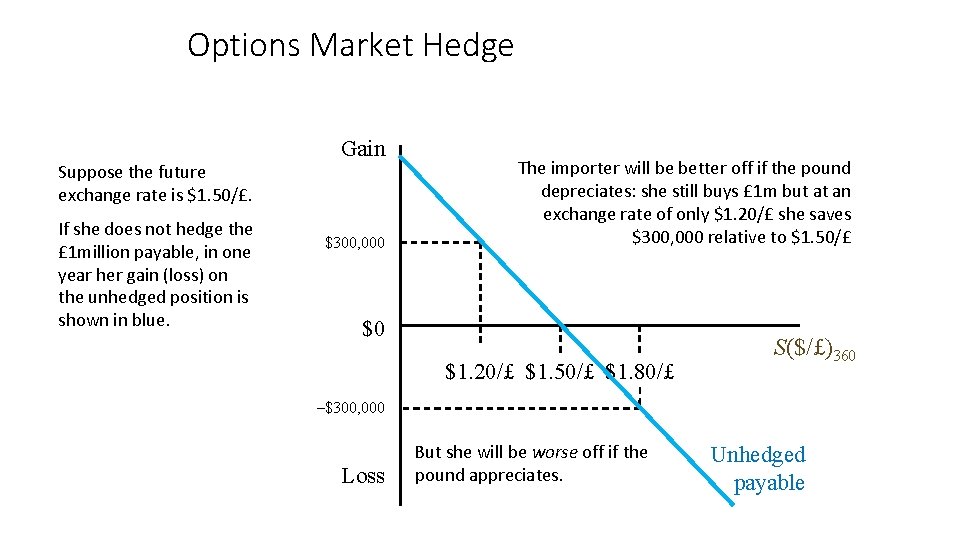
Forward Market Hedge Suppose the forward exchange rate is $1. 50/£. If she does not hedge the £ 1 million payable, in one year her gain (loss) on the unhedged position is shown in blue. Gain $300, 000 The importer will be better off if the pound depreciates: she still buys £ 1 m but at an exchange rate of only $1. 20/£ she saves $300, 000 relative to $1. 50/£ $0 $1. 20/£ $1. 50/£ $1. 80/£ S($/£)360 –$300, 000 Loss But she will be worse off if the pound appreciates. Unhedged payable

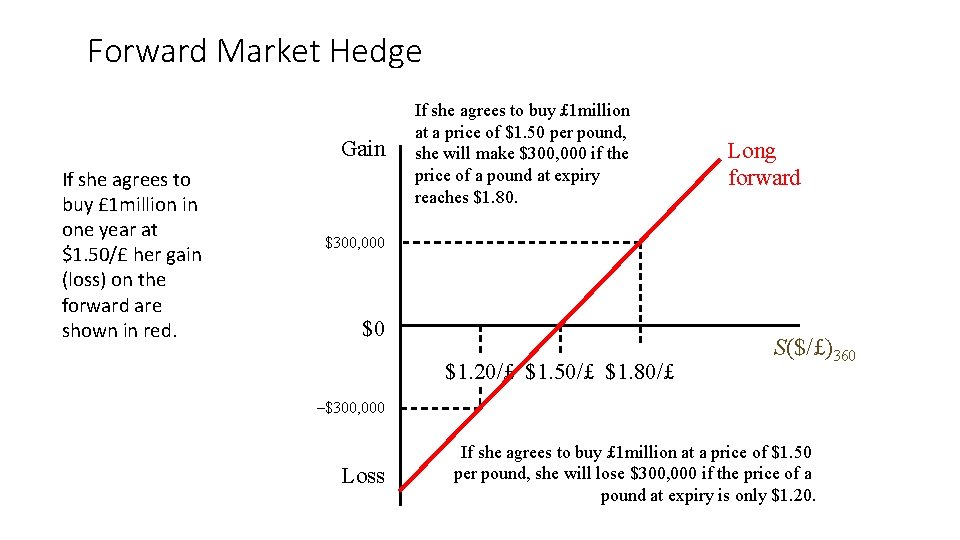
Forward Market Hedge: an Example A U. S. importer of British candles has just ordered next year’s inventory. Payment of £ 1 million is due in one year. Question: How can she fix the cash outflow in dollars? Answer: One way is to put yourself in a position that delivers £ 1 million in one year—a long forward contract on the pound.

Forward Market Hedge Gain If she agrees to buy £ 1 million in one year at $1. 50/£ her gain (loss) on the forward are shown in red. If she agrees to buy £ 1 million at a price of $1. 50 per pound, she will make $300, 000 if the price of a pound at expiry reaches $1. 80. Long forward $300, 000 $0 $1. 20/£ $1. 50/£ $1. 80/£ S($/£)360 –$300, 000 Loss If she agrees to buy £ 1 million at a price of $1. 50 per pound, she will lose $300, 000 if the price of a pound at expiry is only $1. 20.

Forward Market Hedge The purple line shows the payoff of the hedged payable. Note that gains on one position are offset by losses on the other position. Blue and red make purple. Gain Long forward $300, 000 $0 Hedged payable $1. 20/£ $1. 50/£ $1. 80/£ S($/£)360 –$300, 000 Loss Unhedged payable

Options

The nature of options • Options differ from futures because they provide asymmetric cover against price movements. • Options limit the effects of adverse price movements without reducing profits from favourable price movements. • Options involve the payment of a premium by the buyer to the seller (writer).

The nature of options • An option gives the buyer the right, but not the obligation, to buy or sell a specified commodity or financial instrument at a predetermined price (exercise or strike price), on or before a specified date (expiration date). • An option will be exercised only if it is in the buyer’s best interests. • Buyer of an option entered into a contract to sell 100 ounces of gold at USD 1200 per ounce in six months (exercise price is USD 1200), • If in six months the price of gold in the physical market has fallen to USD 1150, the buyer of the option would exercise the option and sell the gold at the higher exercise price, • However, if the price of gold was USD 1275 per ounce on the exercise date, the option holder would let the option lapse and sell the gold directly into the physical market at the higher current price.

The nature of options • Types of options • Call options give the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future, at prices agreed upon today (the exercise price) • Put options give the holder the right, but not the obligation, to sell a given quantity of some asset at some time in the future, at prices agreed upon today (the exercise price)

The nature of options • Premium • The price paid by an option buyer to the writer (seller) of the option • Exercise price or strike price • The price specified in an options contract at which the option buyer can buy or sell • Options can be exercised either: • only on expiration date (European) • any time up to expiration date (American) • since this option to exercise early generally has value, American options are usually worth more than European options, other things equal

Organization of the market • Option markets are categorised as: • Over the counter • Trade options not traded on the exchanges, e. g. semi-government securities and other money-market instruments or securities with unusual maturities • Allows flexibility in terms of: • • amount term interest rate price • Used to set risk caps, floors and collars • Exchange-traded • These are recorded through a clearing house. • Clearing house acts as counterparty to buyer and seller, thus creating two options contracts through the process of ‘novation’. • The clearing house allows buyers and sellers to close out (i. e. reverse) their contracts. Copyright 2009 Mc. Graw-Hill Australia Pty Ltd PPTs t/a Financial Institutions, Instruments and Markets 6 e by Viney Slides prepared by Anthony Stanger

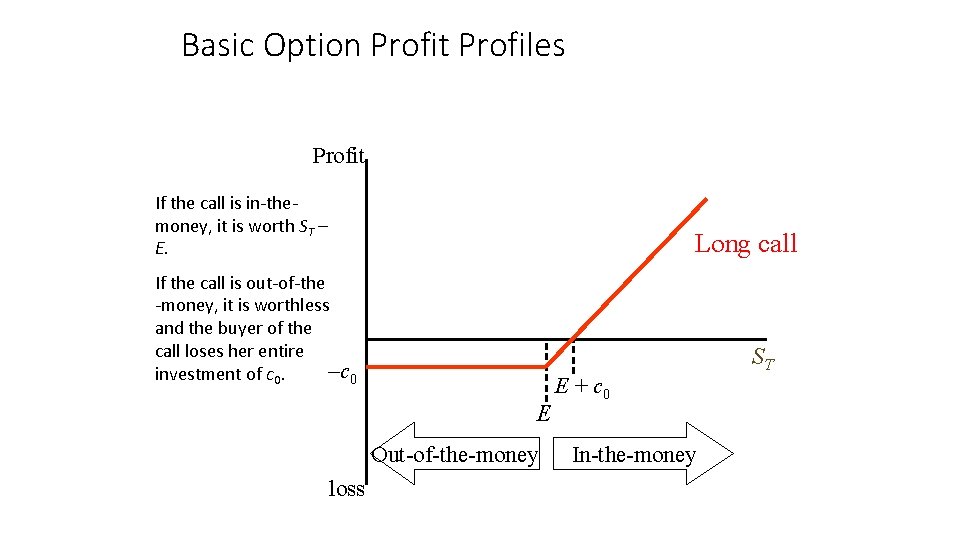
Basic Option Profit Profiles Profit If the call is in-themoney, it is worth ST – E. Long call If the call is out-of-the -money, it is worthless and the buyer of the call loses her entire –c 0 investment of c 0. E Out-of-the-money loss E + c 0 In-the-money ST

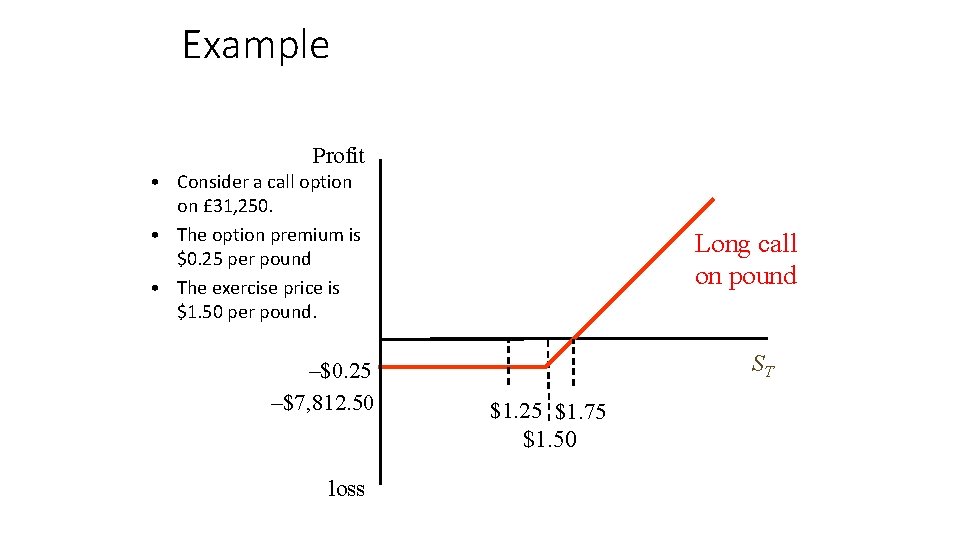
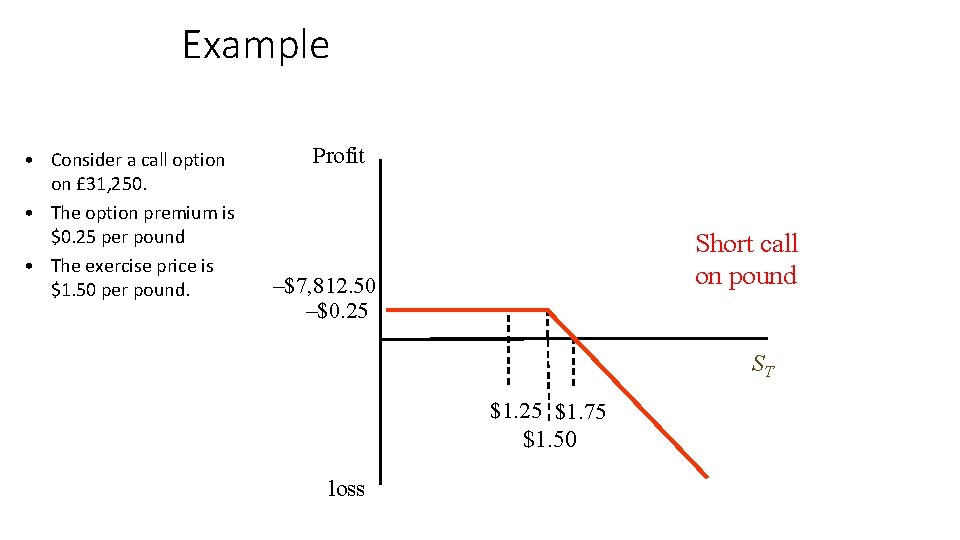
Example Profit • Consider a call option on £ 31, 250. • The option premium is $0. 25 per pound • The exercise price is $1. 50 per pound. –$0. 25 –$7, 812. 50 loss Long call on pound ST $1. 25 $1. 75 $1. 50

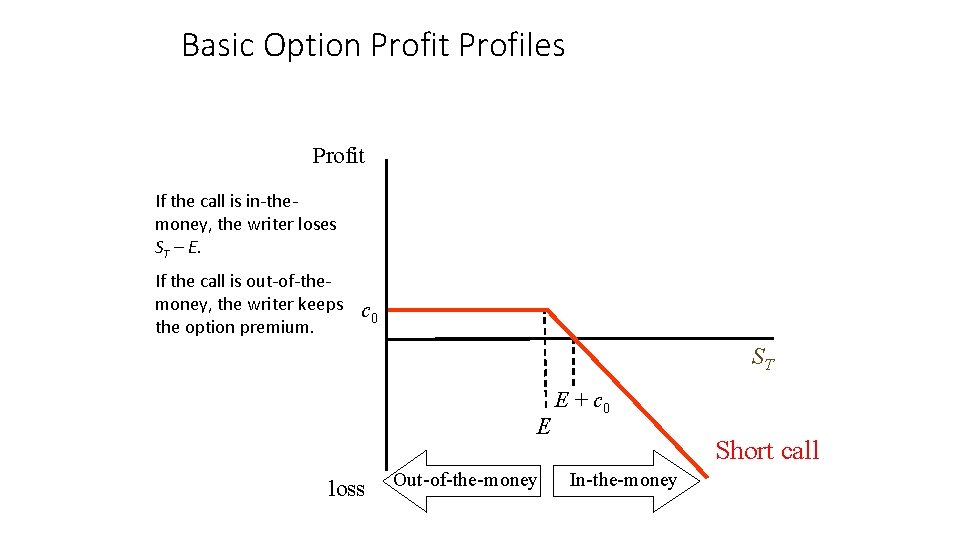
Basic Option Profit Profiles Profit If the call is in-themoney, the writer loses ST – E. If the call is out-of-themoney, the writer keeps the option premium. c 0 ST E loss Out-of-the-money E + c 0 Short call In-the-money

Example • Consider a call option on £ 31, 250. • The option premium is $0. 25 per pound • The exercise price is $1. 50 per pound. Profit Short call on pound –$7, 812. 50 –$0. 25 ST $1. 25 $1. 75 $1. 50 loss

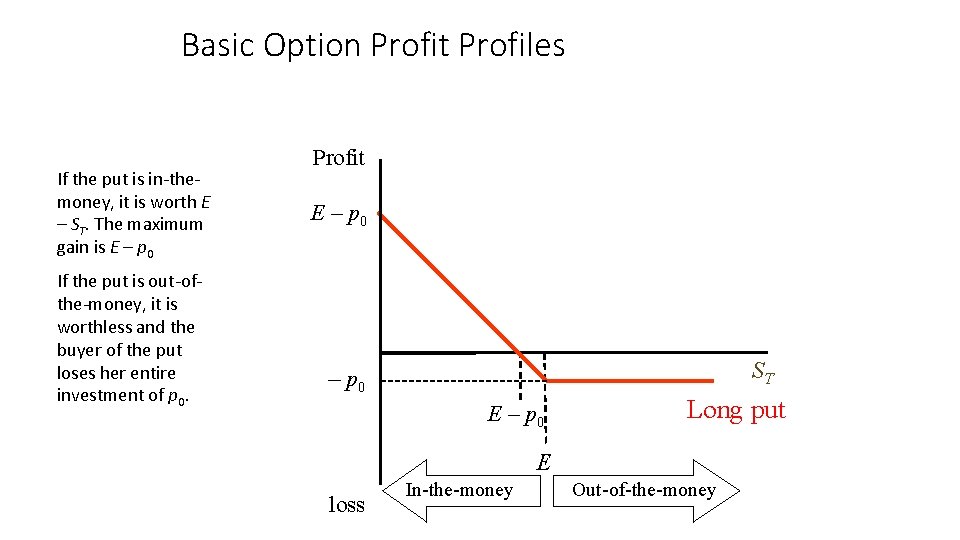
Basic Option Profit Profiles If the put is in-themoney, it is worth E – ST. The maximum gain is E – p 0 If the put is out-ofthe-money, it is worthless and the buyer of the put loses her entire investment of p 0. Profit E – p 0 ST – p 0 E – p 0 Long put E loss In-the-money Out-of-the-money

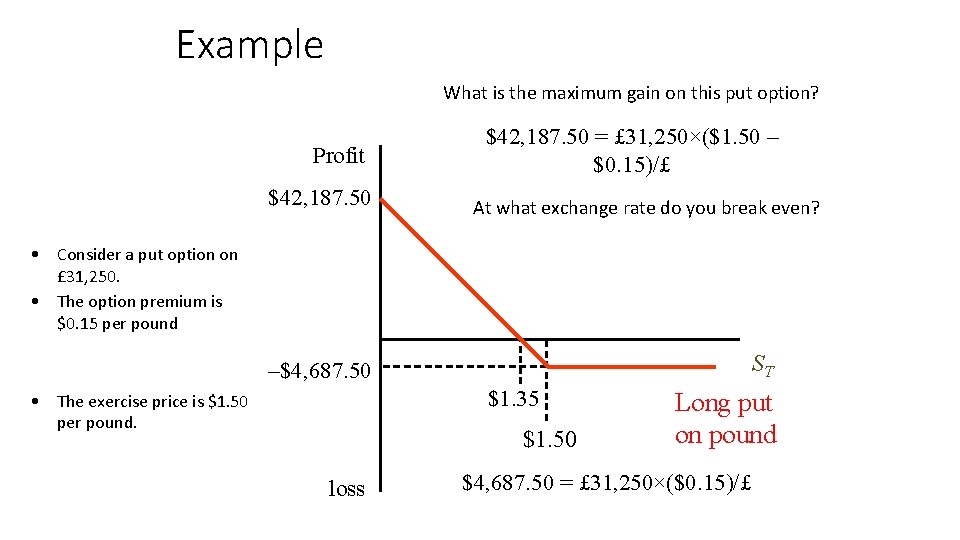
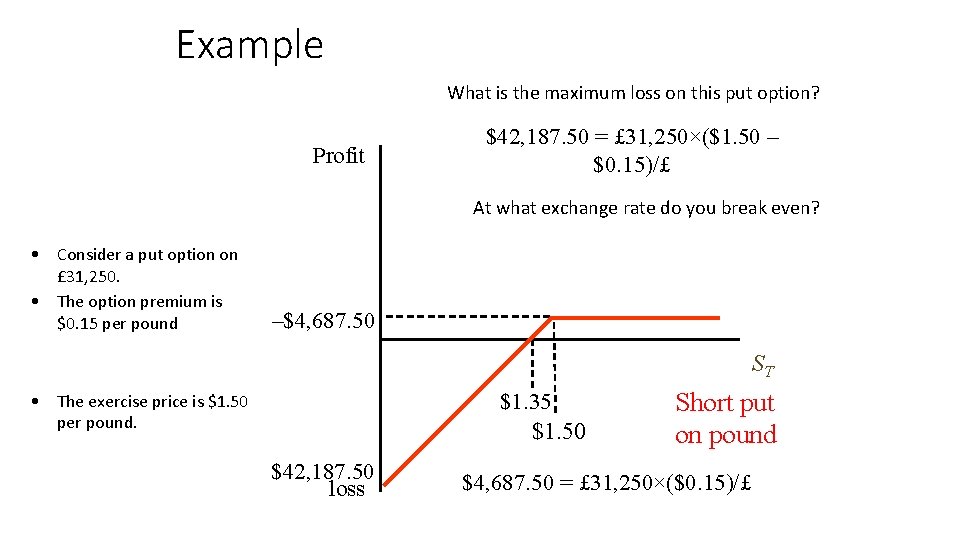
Example What is the maximum gain on this put option? Profit $42, 187. 50 = £ 31, 250×($1. 50 – $0. 15)/£ At what exchange rate do you break even? • Consider a put option on £ 31, 250. • The option premium is $0. 15 per pound ST –$4, 687. 50 $1. 35 • The exercise price is $1. 50 per pound. $1. 50 loss Long put on pound $4, 687. 50 = £ 31, 250×($0. 15)/£

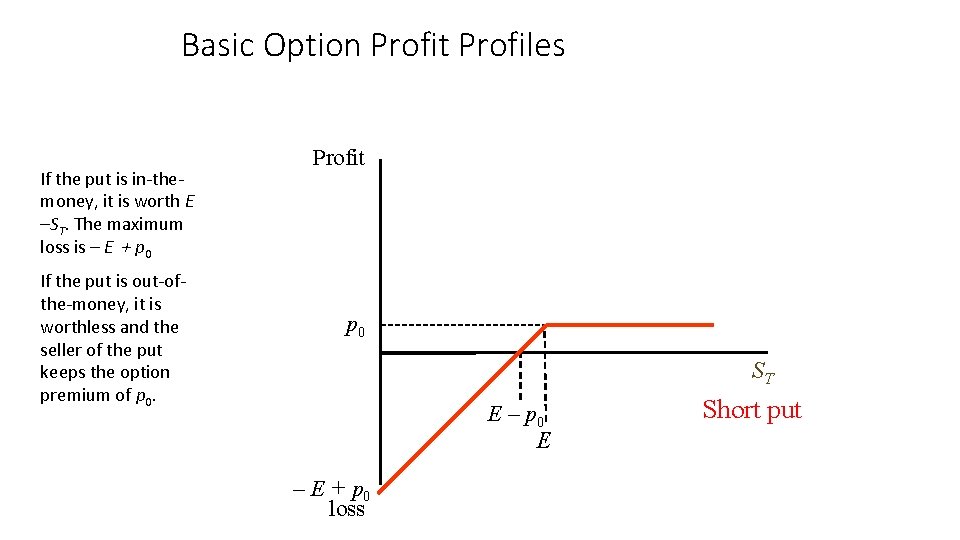
Basic Option Profit Profiles If the put is in-themoney, it is worth E –ST. The maximum loss is – E + p 0 If the put is out-ofthe-money, it is worthless and the seller of the put keeps the option premium of p 0. Profit p 0 ST E – p 0 E – E + p 0 loss Short put

Example What is the maximum loss on this put option? Profit $42, 187. 50 = £ 31, 250×($1. 50 – $0. 15)/£ At what exchange rate do you break even? • Consider a put option on £ 31, 250. • The option premium is $0. 15 per pound –$4, 687. 50 ST $1. 35 $1. 50 • The exercise price is $1. 50 per pound. $42, 187. 50 loss Short put on pound $4, 687. 50 = £ 31, 250×($0. 15)/£

Factors affecting an option contract premium 1. Intrinsic value • The market price of the underlying asset relative to the exercise price • The greater the intrinsic value, the greater the premium, i. e. positive relationship • Options with an intrinsic value • Positive are ‘in the money’ and the buyer is able to exercise contract at a profit • Negative are ‘out of the money’ and the buyer will not exercise • Zero are ‘at the money’

Factors affecting an option contract premium 2. Time value • The longer the time to expiry, the greater the possibility that the option will be able to be exercised for a profit (‘in the money’); i. e. positive relationship. • If the spot price moves adversely, the loss is limited to the premium.

Factors affecting an option contract premium 3. Price volatility • The greater the volatility of the spot price, the greater the chance of exercising the option for a profit, or a loss. • The option will be exercised only if the price moves favourably. • The greater the spot price volatility, the greater the option premium; i. e. positive relationship.

Factors affecting an option contract premium 4. Interest rates - interest rates have opposite impacts on put and call options • Positive relationship between interest rates and the price of a call • If optimistic about the prospects of a rise in the price of a particular asset, can purchase the asset in the physical market now and hold it until the expected price rise eventuates or until expectations change or buy a call option. Locking up money… • Option allows the investor to benefit if the price of the asset moves above the exercise price and does not have to pay for the underlying asset during the period between the contract commencement and the exercising of the option. The funds conserved through this strategy (minus premium) could be invested in the money markets and would thus earn a positive rate of return for the investor. • Negative relationship between interest rates and the price of a put • Buyer of the put option owns the asset specified in the option. Higher interest rates impose a greater cost on the asset-owning individual. By holding an asset, such as shares, the investor has forgone the opportunity of having the funds in the money markets or other interest-earning assets that would earn the higher rate of interest. Opportunity cost of holding asset • Lower present value of the profit if exercised

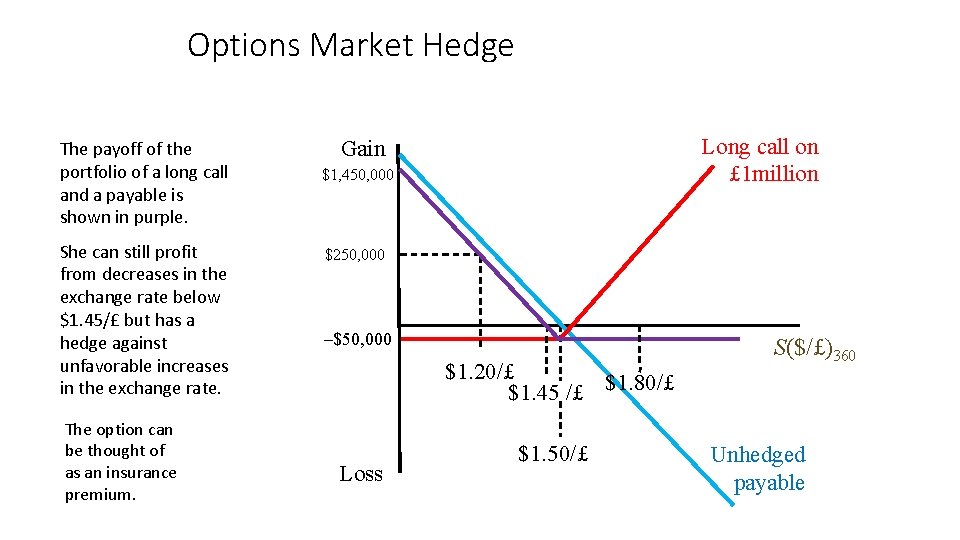
Options Market Hedge • Options provide a flexible hedge against the downside, while preserving the upside potential. • To hedge a foreign currency payable buy calls on the currency. • If the currency appreciates, your call option lets you buy the currency at the exercise price of the call. • To hedge a foreign currency receivable buy puts on the currency. • If the currency depreciates, your put option lets you sell the currency for the exercise price.

Options Market Hedge Suppose the future exchange rate is $1. 50/£. If she does not hedge the £ 1 million payable, in one year her gain (loss) on the unhedged position is shown in blue. Gain $300, 000 The importer will be better off if the pound depreciates: she still buys £ 1 m but at an exchange rate of only $1. 20/£ she saves $300, 000 relative to $1. 50/£ $0 $1. 20/£ $1. 50/£ $1. 80/£ S($/£)360 –$300, 000 Loss But she will be worse off if the pound appreciates. Unhedged payable

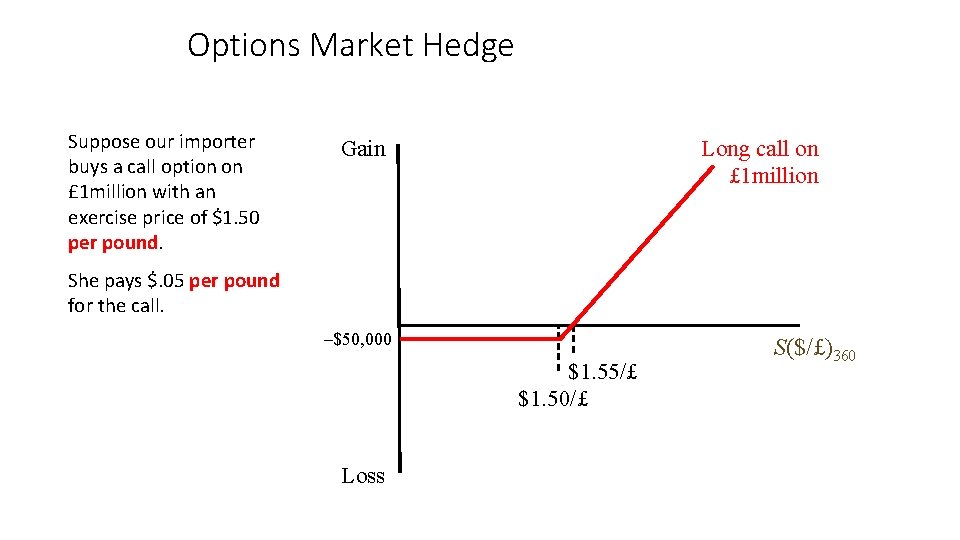
Options Market Hedge Suppose our importer buys a call option on £ 1 million with an exercise price of $1. 50 per pound. Long call on £ 1 million Gain She pays $. 05 per pound for the call. –$50, 000 $1. 55/£ $1. 50/£ Loss S($/£)360

Options Market Hedge The payoff of the portfolio of a long call and a payable is shown in purple. She can still profit from decreases in the exchange rate below $1. 45/£ but has a hedge against unfavorable increases in the exchange rate. The option can be thought of as an insurance premium. Long call on £ 1 million Gain $1, 450, 000 $250, 000 –$50, 000 $1. 20/£ $1. 45 /£ $1. 80/£ Loss $1. 50/£ S($/£)360 Unhedged payable

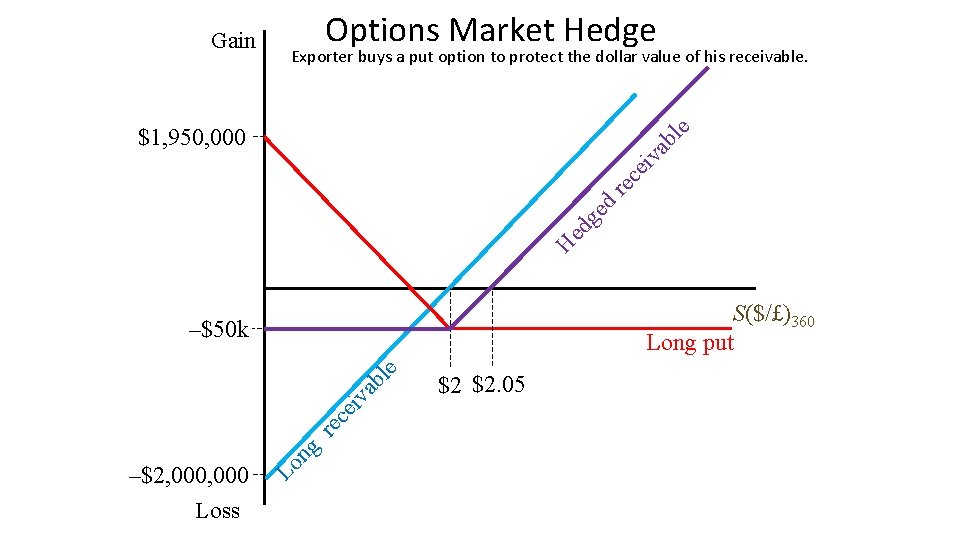
Hedging Exports with Put Options • Show the portfolio payoff of an exporter who is owed £ 1 million in one year. • The current one-year forward rate is £ 1 = $2. • Instead of entering into a short forward contract, he buys a put option written on £ 1 million with a maturity of one year and a strike price of £ 1 = $2. • The cost of this option is $0. 05 per pound Premium = $50, 000

Gain Options Market Hedge Exporter buys a put option to protect the dollar value of his receivable. H ed ge d re ce iv ab l e $1, 950, 000 S($/£)360 Long put –$2, 000 Loss Lo ng re ce iv ab le –$50 k $2 $2. 05

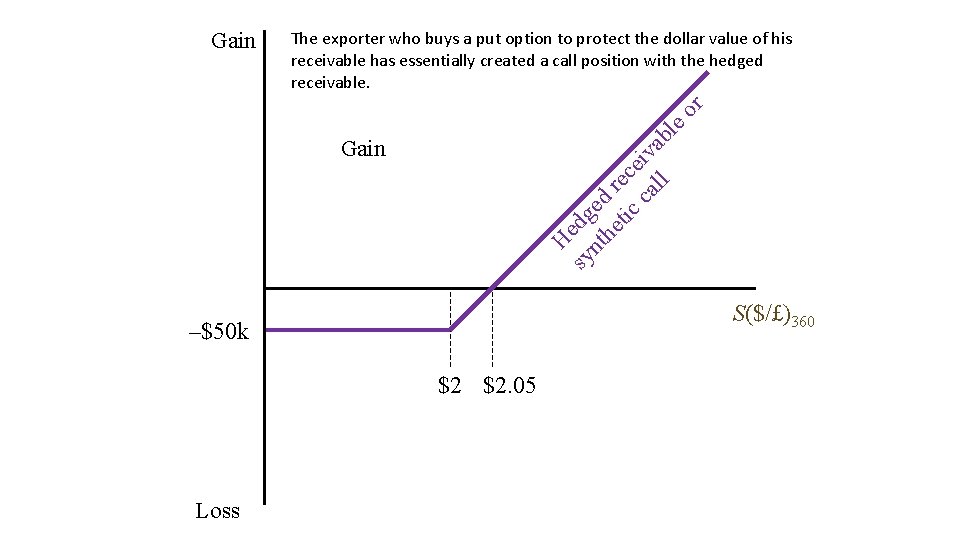
The exporter who buys a put option to protect the dollar value of his receivable has essentially created a call position with the hedged receivable. H sy edg nt ed he r tic ec ca eiv ll ab l eo r Gain S($/£)360 –$50 k $2 $2. 05 Loss

Options Markets Hedge IMPORTERS who OWE foreign currency in the future should BUY CALL OPTIONS. • If the price of the currency goes up, call will lock in an upper limit on the dollar cost of his imports. • If the price of the currency goes down, will have the option to buy the foreign currency at a lower price. EXPORTERS with accounts receivable denominated in foreign currency should BUY PUT OPTIONS. • If the price of the currency goes down, put will lock in a lower limit on the dollar value of his exports. • If the price of the currency goes up, will have the option to sell the foreign currency at a higher price.

Another Example Hedging Imports

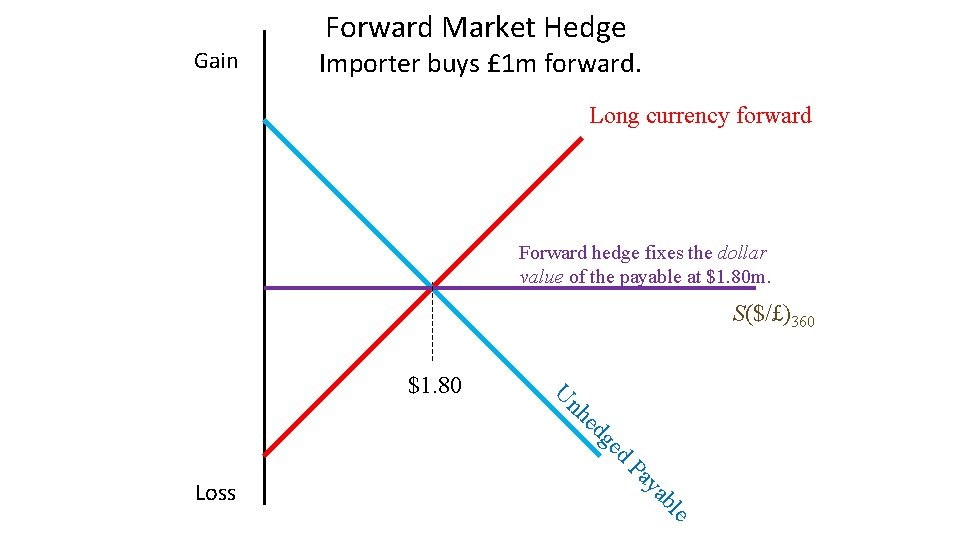
Comparison Hedging Imports with a Forward • Show the portfolio payoff of an importer who owes £ 1 million in one year. • The current one-year forward rate is £ 1 = $1. 80;

Gain Forward Market Hedge Importer buys £ 1 m forward. Long currency forward Forward hedge fixes the dollar value of the payable at $1. 80 m. S($/£)360 d ge ed nh U $1. 80 e bl ya Pa Loss

Comparison Hedging Imports with Call Options • Show the portfolio payoff of an importer who owes £ 1 million in one year. • The current one-year forward rate is £ 1 = $1. 80; • Instead of entering into a short forward contract, buy a call option written on £ 1 million with an expiry of one year and a strike of £ 1 = $1. 80. The cost of this option is $0. 08 per pound.

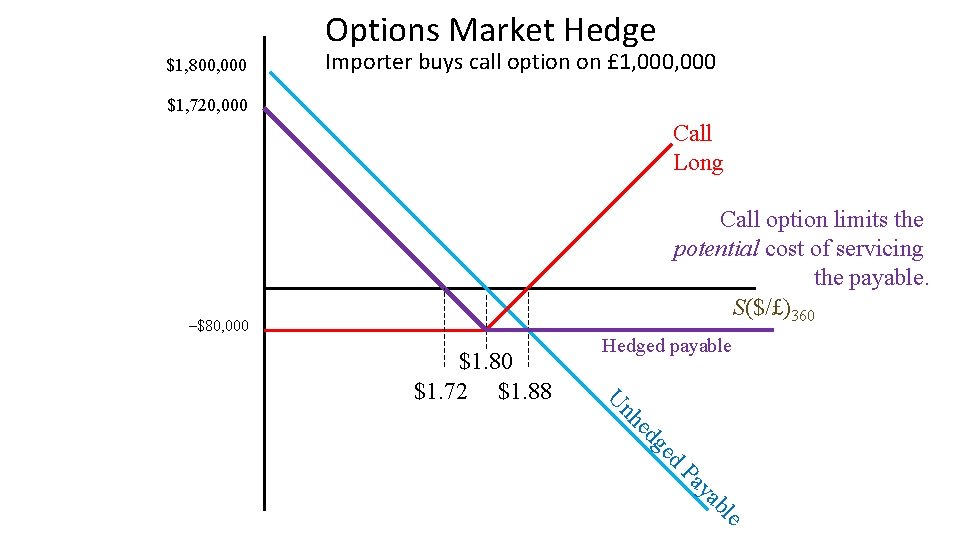
Options Market Hedge $1, 800, 000 Importer buys call option on £ 1, 000 $1, 720, 000 Call Long Call option limits the potential cost of servicing the payable. S($/£)360 –$80, 000 d ge ed nh U $1. 80 $1. 72 $1. 88 Hedged payable e bl ya Pa

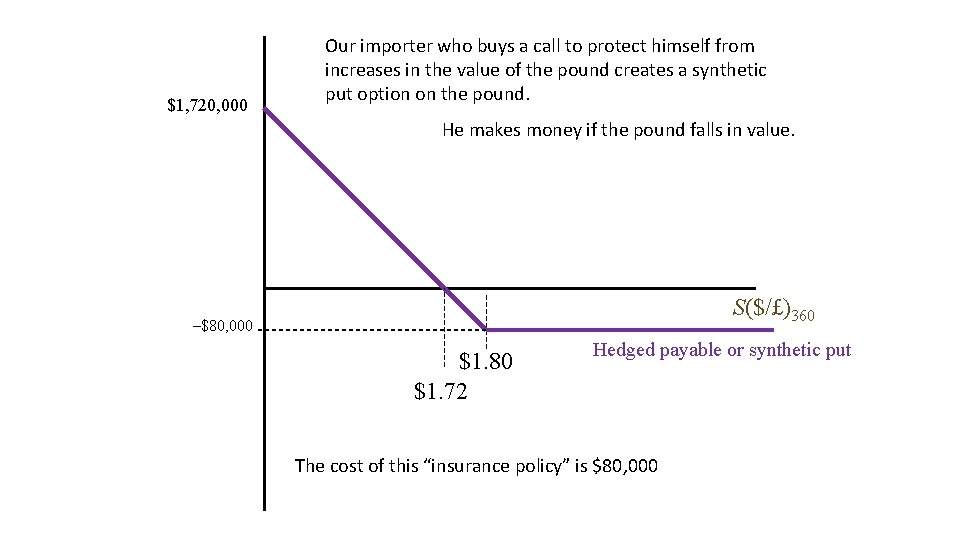
$1, 720, 000 Our importer who buys a call to protect himself from increases in the value of the pound creates a synthetic put option on the pound. He makes money if the pound falls in value. S($/£)360 –$80, 000 $1. 80 $1. 72 Hedged payable or synthetic put The cost of this “insurance policy” is $80, 000