RISK ASSESSMENT OF SEWER CONDITION USING ARTIFICIAL INTELLIGENCE

RISK ASSESSMENT OF SEWER CONDITION USING ARTIFICIAL INTELLIGENCE TOOLS Application to the SANEST sewer system Vitor Sousa IST, UTL José Pedro Matos IST, UTL Nuno Marques Almeida IST, UTL José Saldanha Matos IST, UTL http: //www. toledoblade. com/Police-Fire/2013/07/06/Sewer-repairs-start-after-intersectioncollapse-Copy. html SPN 7 2013 Sheffield, 28 -30 August

OUTLINE 1. Introduction 2. Sewer condition modelling 3. SANEST sewer system 4. Data collection 5. Model design 6. Artificial Neural Networks 7. Support Vector Machines 8. Discriminant analysis 9. Conclusions SPN 7 2013 Sheffield, 28 -30 August

1. INTRODUCTION Wastewater drainage systems asset management strategies Ø Reactive Ø Proactive: l prevention-based (or based on age); l inspection-based (or based on condition); l prediction-based (or based on reliability); The concept of risk has also been used in managing wastewater drainage assets, either: Ø Indirectly – by indentifying critical sewers (managed proactively) and noncritical sewers (managed reactively) Ø Directly – through the development of multicriteria tools accounting also for the consequences of the sewers failures (MARESS - Reyna 1993; RERAUVIS - RERAU 1998; CARE-S - CARE‑S 2005) SPN 7 2013 Sheffield, 28 -30 August

2. SEWER CONDITION MODELLING CATEGORY CLASS Function. Deterministic based Stochastic Data-based Artificial inteligence Genetic programing SPN 7 2013 TYPE Linear regression REFERENCES Chughtay and Zayed (2007 a, 2007 b, 2008) Non-linear regression Newton and Vanier (2006); Wirahadikusumah et al. (2001) Survival function Hörold and Baur (1999); Baur and Herz (2002); Baur et al. (2004); Ana (2009) Ordinal regression Yang (1999); Davies et al. (2001 b); Ariaratnam et al. (2001); Pohls (2001); Ana (2009) Markov chains Wirahadikusumah et al. (2001); Micevski et al. (2002); Coombes et al. (2002); Baik et al. (2006); Koo and Ariaratnam (2006); Newton and Vanier (2006); Tran (2007); Le Gat (2008) Semi-Markov chains Kleiner (2001); Dirksen and Clemens (2008); Ana (2009) Tran (2007); Ana (2009) Najafi and Kulandaivel (2005); Tran et al. (2006); Tran (2007); Ana (2009); Khan et al. (2010) Discriminant analysis Artificial Neural Networks – ANNs Fuzzy Set Yan and Vairavamoorthy (2003); Kleiner et al. (2004 a, 2004 b, 2006) Case Based Reasoning – CBR Support Vector Machines – SVMs Fenner et al. (2007) Mashford et al. (2011) Evolutionary Polynomial Regression Savic et al. (2006); Ugarelli et al. (2008); Savic et al. – EPR (2009) Sheffield, 28 -30 August

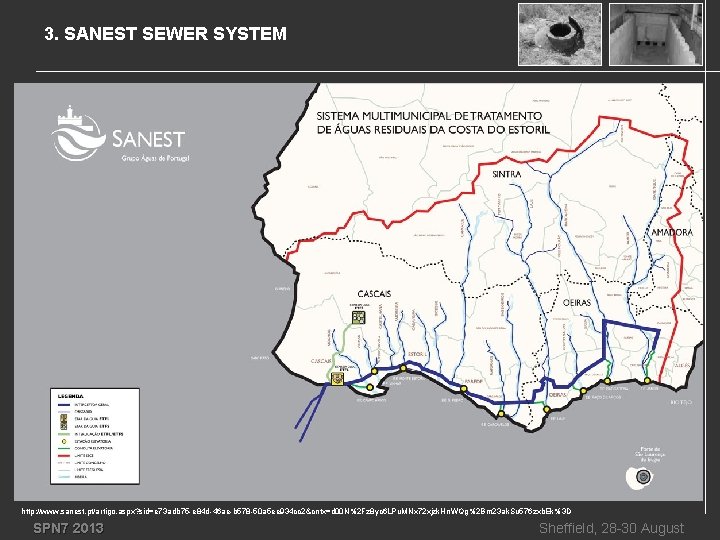
3. SANEST SEWER SYSTEM http: //www. sanest. pt/artigo. aspx? sid=e 73 adb 75 -e 84 d-46 ae-b 578 -50 a 5 ee 934 cc 2&cntx=d 00 N%2 Fz 8 yc 6 LPu. MNx 72 xjzk. Hn. WQg%2 Bm 23 ak. Su 576 zxb. Ek%3 D SPN 7 2013 Sheffield, 28 -30 August

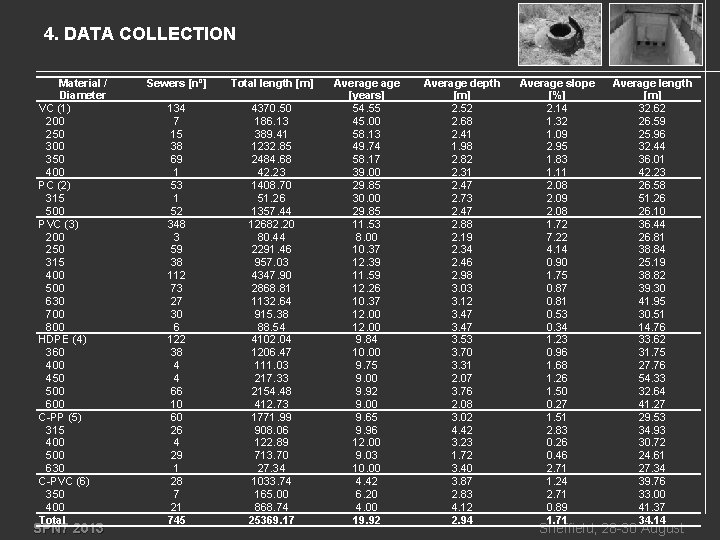
4. DATA COLLECTION Material / Diameter VC (1) 200 250 300 350 400 PC (2) 315 500 PVC (3) 200 250 315 400 500 630 700 800 HDPE (4) 360 400 450 500 600 C-PP (5) 315 400 500 630 C-PVC (6) 350 400 Total SPN 7 2013 Sewers [nº] Total length [m] 134 7 15 38 69 1 53 1 52 348 3 59 38 112 73 27 30 6 122 38 4 4 66 10 60 26 4 29 1 28 7 21 745 4370. 50 186. 13 389. 41 1232. 85 2484. 68 42. 23 1408. 70 51. 26 1357. 44 12682. 20 80. 44 2291. 46 957. 03 4347. 90 2868. 81 1132. 64 915. 38 88. 54 4102. 04 1206. 47 111. 03 217. 33 2154. 48 412. 73 1771. 99 908. 06 122. 89 713. 70 27. 34 1033. 74 165. 00 868. 74 25369. 17 Average [years] 54. 55 45. 00 58. 13 49. 74 58. 17 39. 00 29. 85 30. 00 29. 85 11. 53 8. 00 10. 37 12. 39 11. 59 12. 26 10. 37 12. 00 9. 84 10. 00 9. 75 9. 00 9. 92 9. 00 9. 65 9. 96 12. 00 9. 03 10. 00 4. 42 6. 20 4. 00 19. 92 Average depth [m] 2. 52 2. 68 2. 41 1. 98 2. 82 2. 31 2. 47 2. 73 2. 47 2. 88 2. 19 2. 34 2. 46 2. 98 3. 03 3. 12 3. 47 3. 53 3. 70 3. 31 2. 07 3. 76 2. 08 3. 02 4. 42 3. 23 1. 72 3. 40 3. 87 2. 83 4. 12 2. 94 Average slope [%] 2. 14 1. 32 1. 09 2. 95 1. 83 1. 11 2. 08 2. 09 2. 08 1. 72 7. 22 4. 14 0. 90 1. 75 0. 87 0. 81 0. 53 0. 34 1. 23 0. 96 1. 68 1. 26 1. 50 0. 27 1. 51 2. 83 0. 26 0. 46 2. 71 1. 24 2. 71 0. 89 1. 71 Average length [m] 32. 62 26. 59 25. 96 32. 44 36. 01 42. 23 26. 58 51. 26 26. 10 36. 44 26. 81 38. 84 25. 19 38. 82 39. 30 41. 95 30. 51 14. 76 33. 62 31. 75 27. 76 54. 33 32. 64 41. 27 29. 53 34. 93 30. 72 24. 61 27. 34 39. 76 33. 00 41. 37 34. 14 Sheffield, 28 -30 August

5. MODEL DESIGN The sewer operational and structural condition classes were determined from the CCTV inspection results using the WRc (2001) rating protocol. Two alternative approaches were used to reduce number of condition classes used as outputs: Ø ALT A – the sewers were classified into three categories representing reaches that are in good condition and are expected to endure a long period before the next inspection (category 0 – sewers in condition 1 and 2), sewers that require a shorter period of time until the next inspection (category 1 – sewers in condition 3) and sewers that are failing and should be intervened in the short term (category 2 –sewers in condition 4 and 5) Ø ALT B – the sewers were divided into those that require intervention (category 2 – sewers in condition 4 and 5) and those which do not require intervention (category 1 – sewers in condition 1, 2 and 3). SPN 7 2013 Sheffield, 28 -30 August

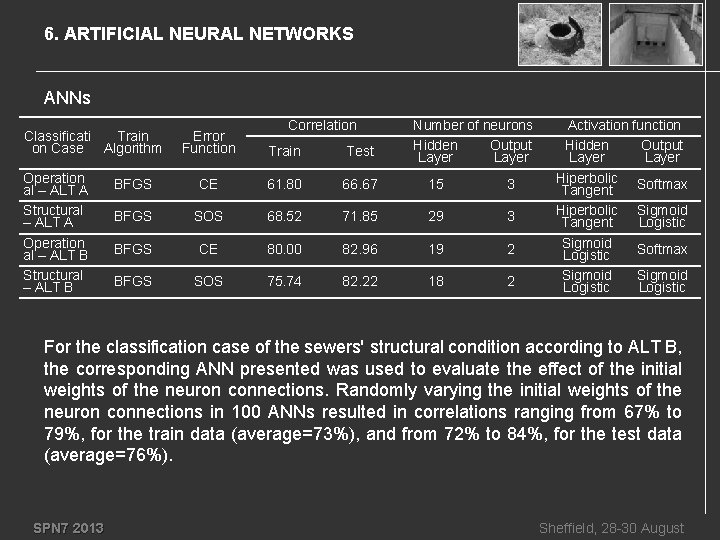
6. ARTIFICIAL NEURAL NETWORKS ANNs Classificati Train on Case Algorithm Operation al – ALT A Structural – ALT A Operation al – ALT B Structural – ALT B Correlation Number of neurons Hidden Output Layer Error Function Train Test BFGS CE 61. 80 66. 67 15 3 BFGS SOS 68. 52 71. 85 29 3 BFGS CE 80. 00 82. 96 19 2 BFGS SOS 75. 74 82. 22 18 2 Activation function Hidden Output Layer Hiperbolic Softmax Tangent Hiperbolic Sigmoid Tangent Logistic Sigmoid Softmax Logistic Sigmoid Logistic For the classification case of the sewers' structural condition according to ALT B, the corresponding ANN presented was used to evaluate the effect of the initial weights of the neuron connections. Randomly varying the initial weights of the neuron connections in 100 ANNs resulted in correlations ranging from 67% to 79%, for the train data (average=73%), and from 72% to 84%, for the test data (average=76%). SPN 7 2013 Sheffield, 28 -30 August

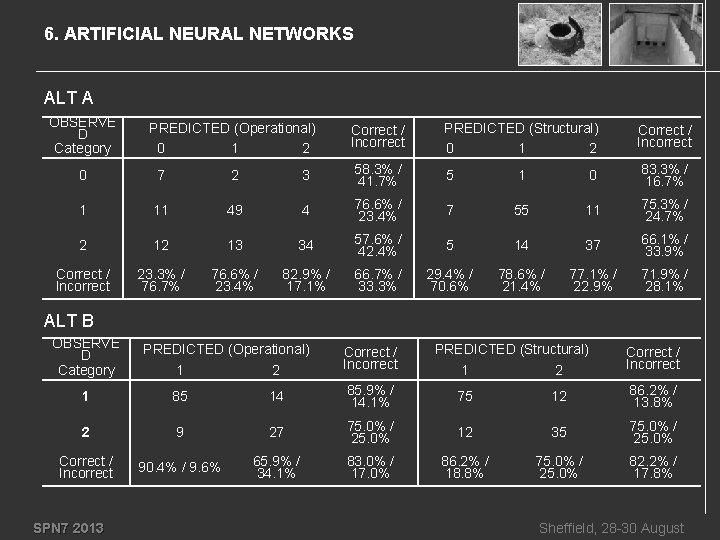
6. ARTIFICIAL NEURAL NETWORKS ALT A OBSERVE D Category PREDICTED (Operational) 0 1 2 Correct / Incorrect PREDICTED (Structural) 0 1 2 Correct / Incorrect 0 7 2 3 58. 3% / 41. 7% 5 1 0 83. 3% / 16. 7% 1 11 49 4 76. 6% / 23. 4% 7 55 11 75. 3% / 24. 7% 2 12 13 34 57. 6% / 42. 4% 5 14 37 66. 1% / 33. 9% Correct / Incorrect 23. 3% / 76. 7% 76. 6% / 23. 4% 82. 9% / 17. 1% 66. 7% / 33. 3% 29. 4% / 70. 6% 78. 6% / 21. 4% 77. 1% / 22. 9% 71. 9% / 28. 1% ALT B OBSERVE D Category PREDICTED (Operational) 1 2 Correct / Incorrect PREDICTED (Structural) 1 2 Correct / Incorrect 1 85 14 85. 9% / 14. 1% 75 12 86. 2% / 13. 8% 2 9 27 75. 0% / 25. 0% 12 35 75. 0% / 25. 0% Correct / Incorrect 90. 4% / 9. 6% 65. 9% / 34. 1% 83. 0% / 17. 0% 86. 2% / 18. 8% 75. 0% / 25. 0% 82. 2% / 17. 8% SPN 7 2013 Sheffield, 28 -30 August

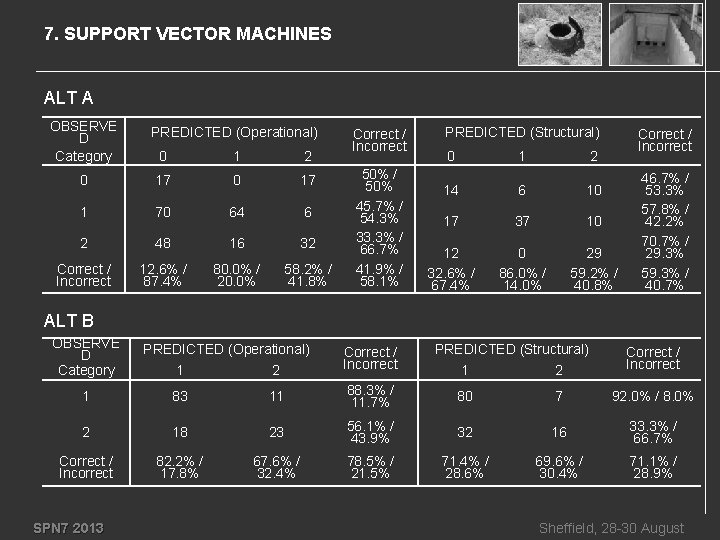
7. SUPPORT VECTOR MACHINES ALT A OBSERVE D Category PREDICTED (Operational) 0 1 2 0 17 1 70 64 6 2 48 16 32 Correct / Incorrect 12. 6% / 87. 4% 80. 0% / 20. 0% 58. 2% / 41. 8% Correct / Incorrect 50% / 50% 45. 7% / 54. 3% 33. 3% / 66. 7% 41. 9% / 58. 1% PREDICTED (Structural) Correct / Incorrect 0 1 2 14 6 10 17 37 10 12 32. 6% / 67. 4% 0 86. 0% / 14. 0% 29 59. 2% / 40. 8% 46. 7% / 53. 3% 57. 8% / 42. 2% 70. 7% / 29. 3% 59. 3% / 40. 7% ALT B OBSERVE D Category PREDICTED (Operational) 1 2 Correct / Incorrect PREDICTED (Structural) 1 2 Correct / Incorrect 1 83 11 88. 3% / 11. 7% 80 7 92. 0% / 8. 0% 2 18 23 56. 1% / 43. 9% 32 16 33. 3% / 66. 7% Correct / Incorrect 82. 2% / 17. 8% 67. 6% / 32. 4% 78. 5% / 21. 5% 71. 4% / 28. 6% 69. 6% / 30. 4% 71. 1% / 28. 9% SPN 7 2013 Sheffield, 28 -30 August

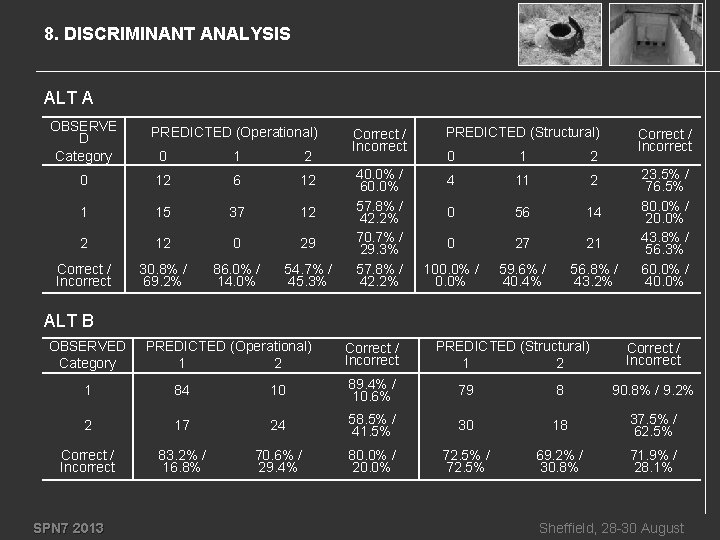
8. DISCRIMINANT ANALYSIS ALT A OBSERVE D Category PREDICTED (Operational) 0 1 2 0 12 6 12 1 15 37 12 2 12 0 29 Correct / Incorrect 30. 8% / 69. 2% 86. 0% / 14. 0% 54. 7% / 45. 3% Correct / Incorrect PREDICTED (Structural) 0 1 2 40. 0% / 60. 0% 57. 8% / 42. 2% 70. 7% / 29. 3% 57. 8% / 42. 2% 4 11 2 0 56 14 0 27 21 100. 0% / 0. 0% 59. 6% / 40. 4% 56. 8% / 43. 2% Correct / Incorrect 23. 5% / 76. 5% 80. 0% / 20. 0% 43. 8% / 56. 3% 60. 0% / 40. 0% ALT B OBSERVED Category PREDICTED (Operational) 1 2 Correct / Incorrect PREDICTED (Structural) 1 2 Correct / Incorrect 1 84 10 89. 4% / 10. 6% 79 8 90. 8% / 9. 2% 2 17 24 58. 5% / 41. 5% 30 18 37. 5% / 62. 5% Correct / Incorrect 83. 2% / 16. 8% 70. 6% / 29. 4% 80. 0% / 20. 0% 72. 5% / 72. 5% 69. 2% / 30. 8% 71. 9% / 28. 1% SPN 7 2013 Sheffield, 28 -30 August

9. CONCLUSIONS The different methods yielded very similar overall result. Since the main goal of modelling the condition of sewers is to identify the sewer reaches that may need intervention, the ANNs’ results provided better results given the approach adopted. However, contrarily to the SVMs and discriminant analysis, the ANNs’ results depend significantly in various factors. The increase of the number of classes resulted in a decrease in the models accuracy. SPN 7 2013 Sheffield, 28 -30 August

REFERENCES Ana, E. V. (2009). Sewer asset management - sewer structural deterioration modeling and multicriteria decision making in sewer rehabilitation projects prioritization. Ph. D Thesis, Faculty of Engineering, Vrije Universiteit Brussel, Brussels, Belgium. Ariaratnam, T. S. ; Assaly, E. A. ; Yuqing, Y. (2001). Assessment of infrastructure inspection needs using logistic models. Journal of Infrastructure Systems, 7(4): 66 -72. Baik, H. S. ; Jeong, H. S. ; Abraham, D. M. (2006). Estimating transition probabilities in markov chainbased deterioration models for management of wastewater systems. Journal of Water Resources Planning and Management, 132(1): 15 -24. Baur, R. ; Herz, R. (2002). Selective inspection planning with ageing forecast for sewer types. Water Science and Technology, 46(6 -7): 379 -387. Baur, R. ; Zielichowski-Haber, W. ; Kropp, I. (2004). Statistical analysis of inspection data for the asset management of sewer networks. In Proceedings 19 th EJSW on Process Data and Integrated Urban Water Modeling, Lyon, France. Chughtai, F; Zayed, T. (2007 a). Structural condition models for sewer pipeline. Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects, 8– 11 July, Boston, USA. Chughtai, F; Zayed, T. (2007 b). Sewer pipeline operational condition prediction using multiple regression. Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects, 8– 11 July, Boston, USA. Chughtai, F; Zayed, T. (2008). Infrastructure condition prediction models for sustainable sewer pipelines. Journal of Performance of Constructed Facilities, 22(5): 333 -341. Davies, J. ; Clarke, B. ; Whiter, J. ; Cunningham, R. (2001). The structural condition of rigid sewer pipes: a statistical investigation. Urban Water, 3: 277 -286. Dirksen, J. ; Clemens, F. H. L. R. (2008). Probabilistic modeling of sewer deterioration using inspection SPN 7 2013 Sheffield, 28 -30 August

REFERENCES Hörold, S. ; Baur, R. (1999). Modeling sewer deterioration for selective inspection planning – case study Dresden. In Proceedings 13 th EJSW on Service Life Management Strategies of Water Mains and Sewers, 8 -12 September, Switzerland. Khan, Z. ; Zayed, T. ; Moselhi, O. (2010). Structural condition assessment of sewer pipelines. Journal of Performance of Constructed Facilities, 24(2): 170 -179. Kleiner, Y. (2001). Scheduling inspection and renewal of large infrastructure assets. Journal of Infrastructure Systems, 7(4): 136 -143. Kleiner, Y. ; Rajani, B. ; Sadiq, R. (2004 a). Modeling failure risk in buried pipes using fuzzy Markov deterioration process”, 4 th International Conference on Decision Making in Urban and Civil Engineering, 28 -30 October, Porto, Portugal, pp. 1 -11. Kleiner, Y. ; Sadiq, R. ; Rajani, B. (2004 b). Modeling failure risk in buried pipes using fuzzy Markov deterioration process. Pipelines 2004, Conference Proceedings, ASCE, San Diego, California, USA, pp. 7 -16. Kleiner, Y. ; Sadiq, R. ; Rajani, B. B. (2006). Modelling the deterioration of buried infrastructure as a fuzzy Markov process. Journal of Water Supply Research and Technology: Aqua, 55(2): 67 -80. Koo, D. -H. ; Ariaratnam, S. T. (2006). Innovative method for assessment of underground sewer pipe condition. Automation in Construction, 15: 479 -488. Le Gat, Y. (2008). Modelling the deterioration process of drainage pipelines. Urban Water, 5(2): 97 -106. Mashford, J. ; Marlow, D. ; Tran, T. ; May, R. (2011). Prediction of Sewer Condition Grade Using Support Vector Machines. Journal of Computing in Civil Engineering, 25(4): 283 -290. Micevski, T. ; Kuczera, G. ; Coombes, P. (2002). Markov model for storm water pipe deterioration. Journal of Infrastructure Systems, 8(2): 49– 56. multi-objective data mining. Journal of Hydroinformatics, 11(3– 4): 211 -224. SPN 7 2013 Sheffield, 28 -30 August

REFERENCES Pohls, O. (2001). The analysis of tree root blockages in sewer lines & their prevention methods. MSc. Thesis, Institute of Land Food Resources, University of Melbourne, Australia. Savic, D. A. ; Giustolisi, O. ; Laucelli, D. (2009). Asset deterioration analysis using multi-utility data and Savic, D. ; Giustolisi, O. ; Berardi, L. ; Shepherd, W. ; Djordjevic, S. ; Saul, A. (2006). Modelling sewer failure by evolutionary computing. Proceedings of the Institution of Civil Engineers, Water Management, 159(WM 2): 111 -118. Tran, D. H. ; Ng, A. W. M. ; Perera, B. J. C. ; Davis, P. (2006). Application of probabilistic neural networks in modeling structural deterioration of stormwater pipes. Urban Water Journal, 3(3): 175– 184. Tran, H. (2007) Investigation of deterioration models for stormwater pipe systems. Ph. D Thesis, Victoria University, School of Architectural, Civil and Mechanical Engineering Faculty of Health, Engineering and Science, Victoria, Australia. Ugarelli, R. ; Kristensin, S. M. ; Røstum, J. ; Sægrov, S. ; Di Frederico; V. (2008). Statistical analysis and definition of blockages-prediction formulae for the wastewater network of Oslo by evolutionary computing. 11 th International Conference in Urban Drainage, Edinburgh, Scotland, UK. Wirahadikusumah, R. ; Abraham, D. ; Iseley, T. (2001). Challenging issues in modeling deterioration of combined sewers. Journal of Infrastructure Systems, 7(2): 77 -84. Yan, J. ; Vairavamoorthy, K. (2003). Fuzzy approach for pipe condition assessment. Proc. , New Pipeline Technologies, Security, and Safety, ASCE, Reston, Va. , pp. 466– 476. Yang, Y. (1999). Statistical models for assessing sewer infrastructure inspection requirements. MSc. Thesis, Department of Civil and Environmental Engineering, University of Alberta, Edmonton, Alberta, Canada. SPN 7 2013 Sheffield, 28 -30 August

RISK ASSESSMENT OF SEWER CONDITION USING ARTIFICIAL INTELLIGENCE TOOLS Application to the SANEST sewer system Vitor Sousa IST, UTL José Pedro Matos IST, UTL Nuno Marques Almeida IST, UTL José Saldanha Matos IST, UTL http: //www. toledoblade. com/Police-Fire/2013/07/06/Sewer-repairs-start-after-intersectioncollapse-Copy. html SPN 7 2013 Sheffield, 28 -30 August