Risk and Return Part I Expected Return State

Risk and Return – Part (I)

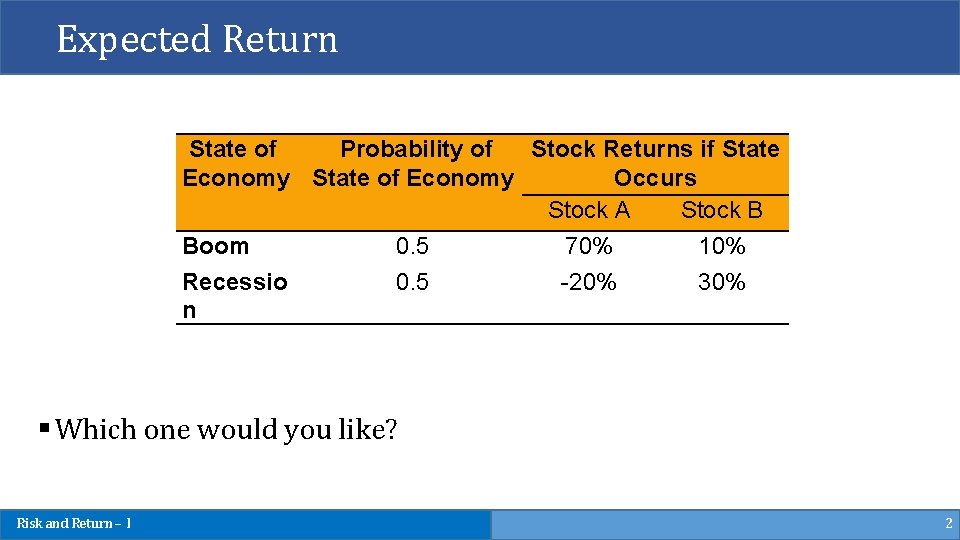
Expected Return State of Probability of Stock Returns if State Economy State of Economy Occurs Stock A Stock B Boom 0. 5 70% 10% Recessio 0. 5 -20% 30% n § Which one would you like? Risk and Return – I 2

Expected Return Risk and Return – I 3

Expected Return – Stock A and B Risk and Return – I 4

Expected Returns § Expected returns are based on the probabilities of possible outcomes. • Where: • pi = the probability of state “i” occurring. • Ri = the expected return on an asset in state i. Risk and Return – I 5

Example 1 § Consider the following information: State of Econom y Recessi on Normal Boom Probability of State of Economy 0. 22 Stock Returns if State Occurs 0. 48 0. 30 14% 33% § Calculate the expected return. Risk and Return – I -12% 6

Answer § E(R) =. 22(– 12%) +. 48(14%) +. 30(33%) = 13. 98% Risk and Return – I 7

Measuring Risk – Variance & Standard Deviation • Variance measures the average squared difference between the actual returns and the expected return • Standard deviation is the square root of variance • The larger the variance or standard deviation is, the more spread out the returns will be State of Probability of Stock Returns if State Economy State of Economy Occurs Stock A Stock B Boom 0. 5 70% 10% Recessio 0. 5 -20% 30% n Risk and Return – I 8

Measuring Risk – Variance & Standard Deviation Risk and Return – I 9

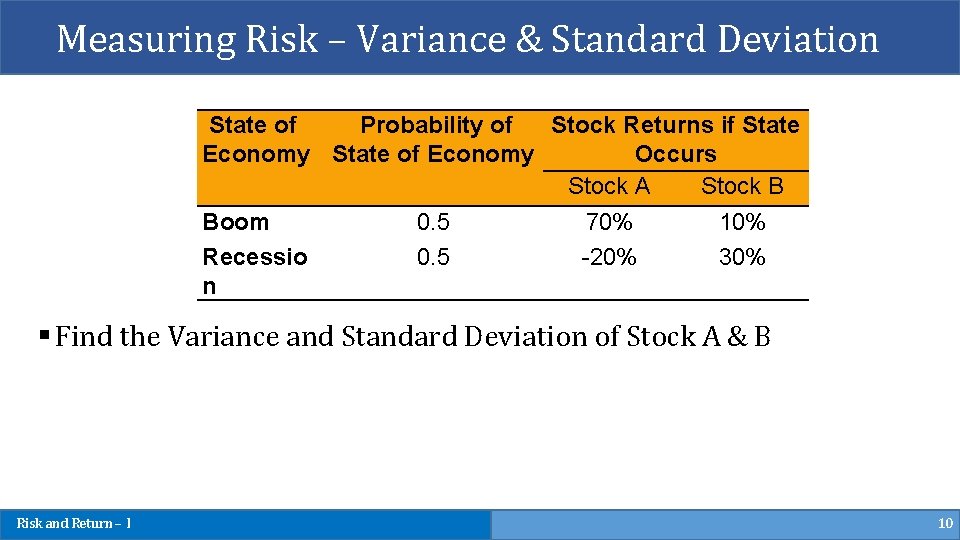
Measuring Risk – Variance & Standard Deviation State of Probability of Stock Returns if State Economy State of Economy Occurs Stock A Stock B Boom 0. 5 70% 10% Recessio 0. 5 -20% 30% n § Find the Variance and Standard Deviation of Stock A & B Risk and Return – I 10

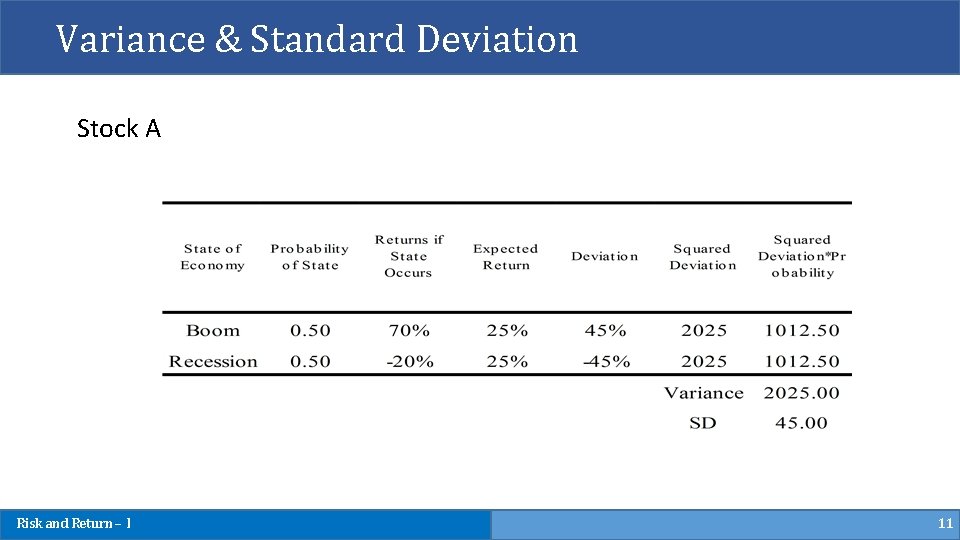
Variance & Standard Deviation Stock A Risk and Return – I 11

Example 2 Consider the following information: State of Probability of Stock Returns if State Economy State of Economy Occurs Stock A Stock B Boom 0. 24 5. 5% -34% Normal 0. 64 13. 5% 24% Recessio 0. 12 23% 47% n Calculate the expected return and standard deviation for two stocks Risk and Return – I 12

Answer Risk and Return – I 13

Portfolio • Portfolio = collection of assets. • An asset’s risk and return impact how the stock affects the risk and return of the portfolio. • The risk-return trade-off for a portfolio is measured by the portfolio expected return and standard deviation, just as with individual assets. Risk and Return – I 14

Portfolio Weight of Individual Asset Risk and Return – I 15

Example 3 § What are the portfolio weights for a portfolio that has 150 shares of Stock A that sell for $87 per share and 125 shares of Stock B that sell for $94 per share? Risk and Return – I 16

Answer • Total value = 150($87) + 125($94) = $24, 800 • x. A = 150($87) / $24, 800 =. 5262 • x. B = 125($94) / $24, 800 =. 4738 Risk and Return – I 17

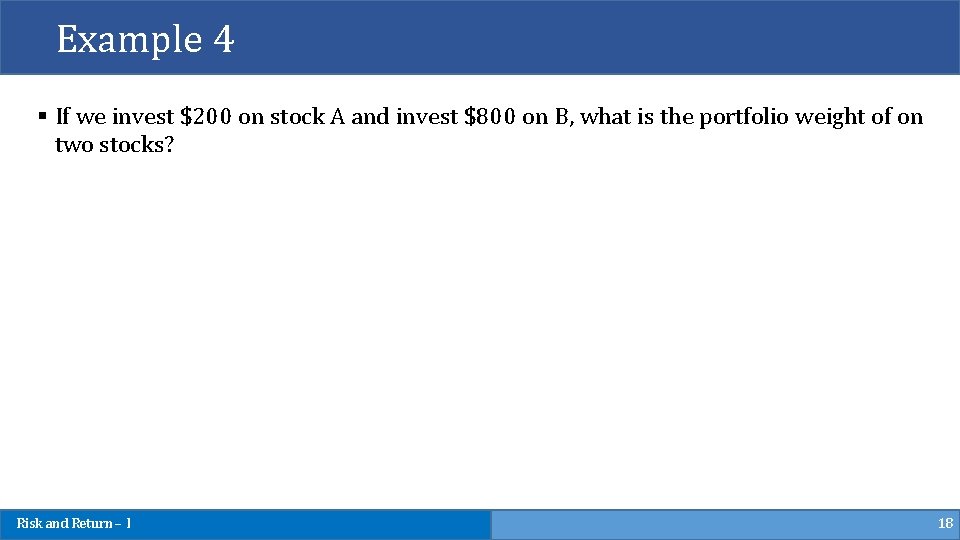
Example 4 § If we invest $200 on stock A and invest $800 on B, what is the portfolio weight of on two stocks? Risk and Return – I 18

Answer Risk and Return – I 19

Example 5 § Continuing Example 4 § Expected return of stocks A is 0. 25 and that of B is 0. 20, what is the portfolio’s expected return? Risk and Return – I 20

Answer Risk and Return – I 21

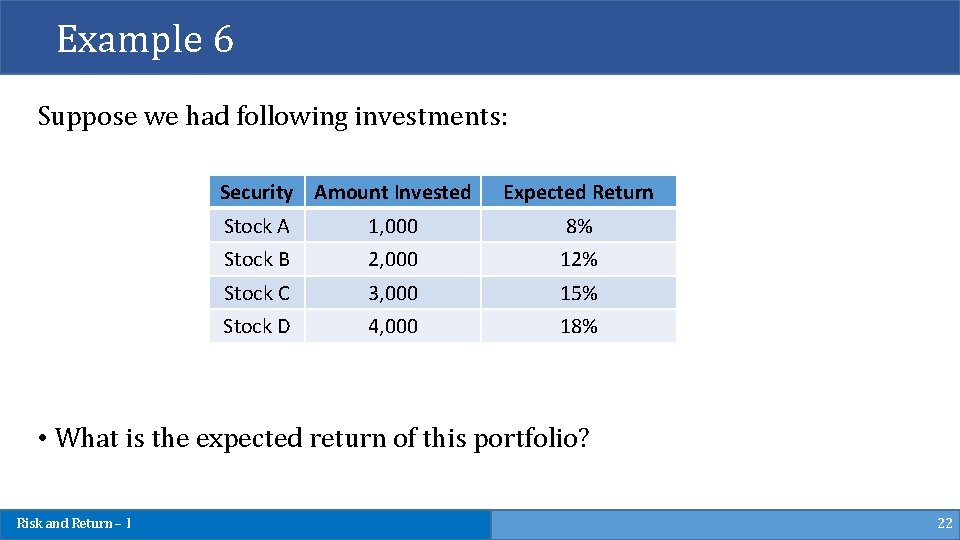
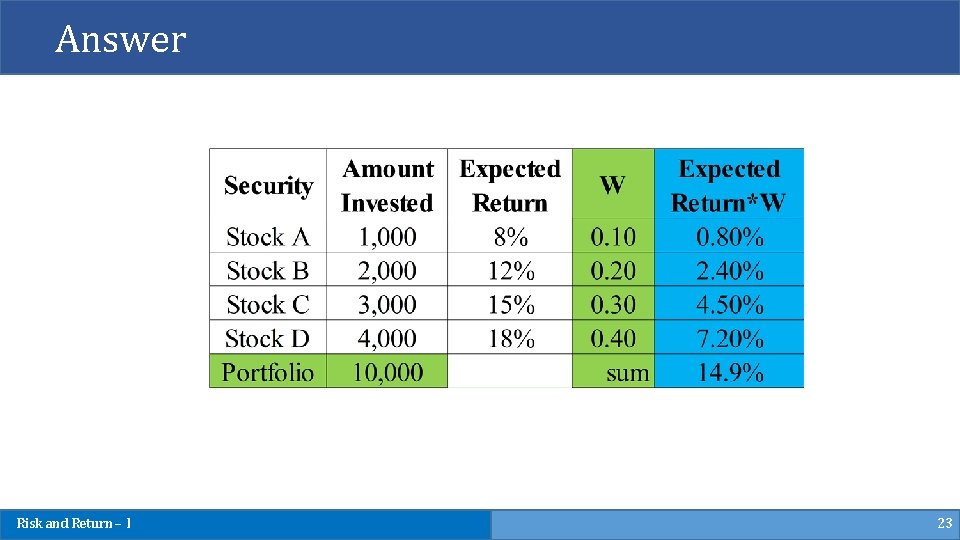
Example 6 Suppose we had following investments: Security Amount Invested Expected Return Stock A 1, 000 8% Stock B 2, 000 12% Stock C 3, 000 15% Stock D 4, 000 18% • What is the expected return of this portfolio? Risk and Return – I 22

Answer Risk and Return – I 23

Example 7 § You have $13, 000 to invest in a stock portfolio. Your choices are Stock X with an expected return of 15% and Stock Y with an expected return of 9%. Assume your goal is to create a portfolio with an expected return of 12. 35%. How much money will you invest in Stock X and Stock Y? Risk and Return – I 24

Answer • E(Rp) = 12. 35 = 15 w. X + 9 (1 – w. X) 12. 35 = 15 w. X + 9 – 9 w. X 3. 35 = 6 w. X • w. X =. 5583 • Investment in X =. 5583($13, 000) = $7, 258. 33 • Investment in Y = (1 –. 5583)($13, 000) = $5, 741. 67 Risk and Return – I 25

Portfolio Risk - Variance and Standard Deviation • Portfolio standard deviation is NOT a weighted average of the standard deviation of the component securities’ risk. • If it were, there would be no benefit to diversification (we will discuss more about it at the next class). Risk and Return – I 26

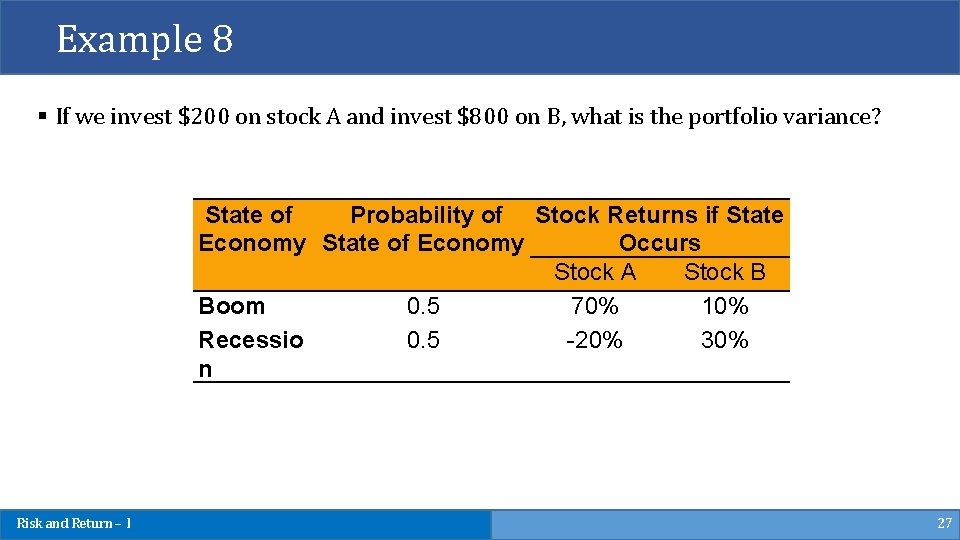
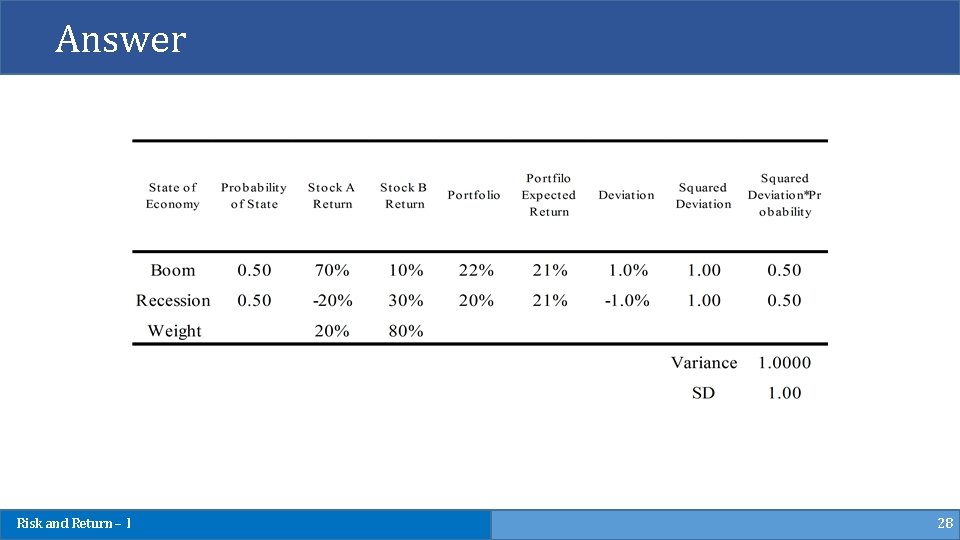
Example 8 § If we invest $200 on stock A and invest $800 on B, what is the portfolio variance? State of Probability of Stock Returns if State Economy State of Economy Occurs Stock A Stock B Boom 0. 5 70% 10% Recessio 0. 5 -20% 30% n Risk and Return – I 27

Answer Risk and Return – I 28

Thanks! 29