RISET OPERASI MODEL JARINGAN MINIMUM SPANNING TREE PROBLEM

RISET OPERASI MODEL JARINGAN MINIMUM SPANNING TREE PROBLEM SHORTEST-PATH PROBL ALGORITMA AUGMENTING PATH

Pengertian Jaringan • Sebuah Jaringan terdiri dari sekelompok node yang dihubungkan oleh busur atau cabang, contoh: • Dalam sistem transportasi, kota mewakili node dan jalan mewakili busur. • Notasi standar untuk menggambarkan jaringan adalah G = (N, A) dimana N adalah himpunan Node dan

Langkah 1, Tentukan Node sebagai salah satu sebagai titik awal dan hubungkan MINIMUM SPANNING TREE dengan node terdekat dalam jaringan PROBLEM tersebut. Dua node yang dihasilkan membentuk kumpulan node yang dihubungkan, dengan kumpulan node yang tidak dihubungkan. Langkah 2, Hubungan antara node yang dihubungkan dengan yang tidak, dengan melihat node yang mempunyai lintasan terpendek. Gabungkan node ini dalam kumpulan node yang dihubungkan. Langkah 3, Ulangi langkah 2 sampai semua node terhubungkan.

CONTOH MINIMUM SPANNING TREE PROBLEM PT. TV Kabel Lampung sedang dalam proses perencanaan penyediaan jaringan jasa TV Kabel ke 6 Wilayah perumahan yang baru. Jaringan sistem Kabel tersebut di tunjukkan dalam gambar. Angkaangka yang berkaitan dengan setiap cabang mewakili jumlah Km Kabel yang diperlukan untuk menghubungkan dua lokasi. Node O mewakili A TV dan 7 node lainnya (A, B, C, D, E, F) stasiun reley 2 F mewakili 2 enam wilayah pengembangan. O 4 B 5 1 4 C 5 3 4 D 7 1 E

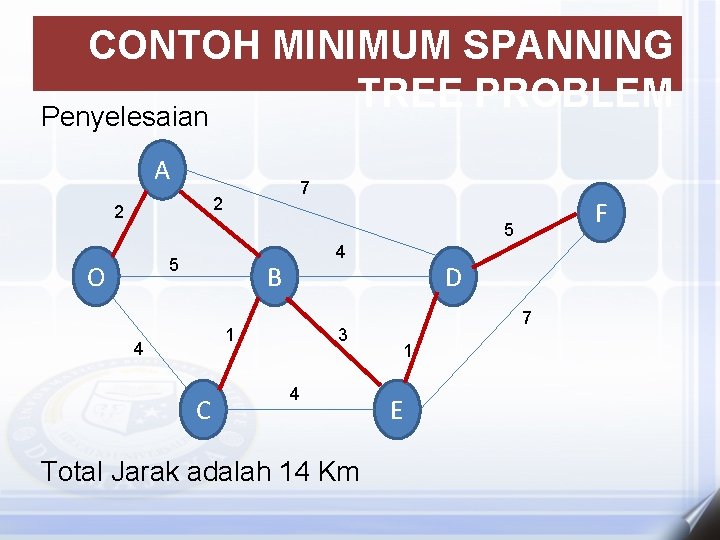
CONTOH MINIMUM SPANNING TREE PROBLEM Penyelesaian A 7 2 2 F 5 5 O 4 B 1 4 C 3 4 Total Jarak adalah 14 Km D 7 1 E

Algoritma Shortest-Path Problem. PROBLEM SHORTEST-PATH Algoritma Asiklis Langkah 1. Buatka label untuk masing node Label node j = [uj, n) dimana uj = Jarak terdekat dari node i ke node j n = node j yang tepat mendahuluinya. Langkah 2, Hitung nilai uj, dimana uj = mini (ui + dij) = un + dnj

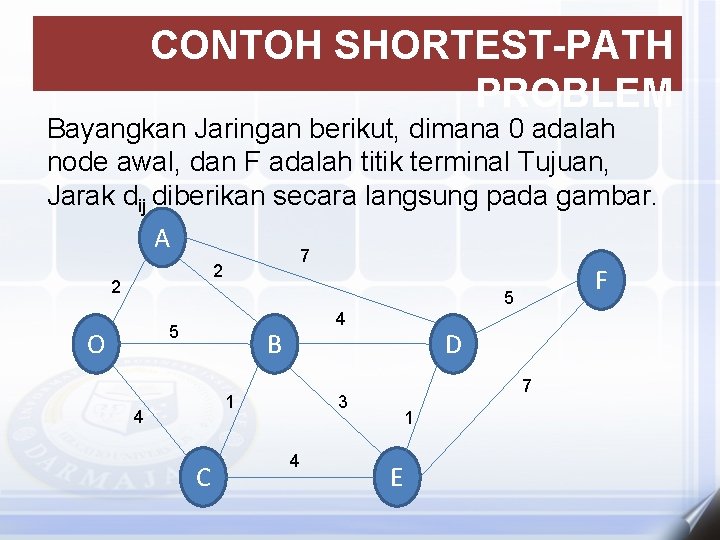
CONTOH SHORTEST-PATH PROBLEM Bayangkan Jaringan berikut, dimana 0 adalah node awal, dan F adalah titik terminal Tujuan, Jarak dij diberikan secara langsung pada gambar. A 7 2 2 F 5 5 O 4 B 1 4 C 3 4 D 7 1 E

CONTOH SHORTEST-PATH PROBLEM Penyelesaian [2, O] [13, D] A 2 2 [0, -] 7 [4, A] 5 O 4 B 1 4 C [4, O] [8, E] 3 4 F 5 D [8, B] 1 E [7, B] 7

CONTOH SHORTEST-PATH PROBLEM Jarak terdekat adalah O-A-B-E-D-F ATAU O-A-B [2, O] [13, D] A 2 2 [0, -] 7 [4, A] 5 O 4 B 1 4 C [4, O] [8, E] 3 4 F 5 D [8, B] 1 E [7, B] 7

CONTOH SHORTEST-PATH PROBLEM Jarak terdekat adalah O-A-B-E-D-F ATAU O-A-B [2, O] [13, D] A 2 2 [0, -] 7 [4, A] 5 O 4 B 1 4 C [4, O] [8, E] 3 4 F 5 D [8, B] 1 E [7, B] 7

memaksimumkan jumlah perjalan titik awal ke tujuan, dimana setiap busur mempunyai kapasitas maksimal jumlah perjalan yang dapat melaluinya. PROBLEM ALIRAN MAKSIMUM Secara umum, masalah aliran digambarkan sebagai berikut: maksimum dapat 1. Semua aliran melalui jaringan terhubung dan terarah berawal dari satu simpul (berawal dari source (sumber) berakhir ke simpul lain yaitu sasaran (tujuan). 2. Simpul lainnya adalam simpul pengiriman. 3. Aliran dari sebuah busur hanya diizinkan pada arah yang ditunjukkan oleh mata panah, dengan jumlah maksimum aliran diberikan oleh kapasitas busur tersebut. 4. Tujuannya adalah memaksimalkan total jumlah aliran dari sumber ke tujuan. Jumlah ini diukur dari salah satu cara yang ekivalen, yaitu jumlah yang meninggalkan sumber atau yang memasuki tujuan.

Implementasi Penerapan dari MAKSIMUM masalah aliran PROBLEM ALIRAN maksimum: 1. Memaksimalkan aliran kendaraan di dalam jaringan transportasi. 2. Memaksimalkan aliran distribusi perusahaan dari pabrik ke konsumen. 3. Memaksimalkan aliran minyak di dalam sistem pipa. 4. Memaksimalkan aliran jaringan persediaan perusahaan dari vendor ke pabrik. 5. Memaksimalkan aliran air dari sistem bendungan.

Algoritma Augmenting Path untuk Masalah Aliran Maksimum 1. Cari augmenting path dengan menemukan beberapa lintasan terarah dari sumber ke tujuan pada jaringan, dimana setiap busur pada lintasan ini mempunyai kapasitas positif. (jika tidak terdapat augmenting path, aliran net yang ditugaskan telah membentuk sebuah pola aliran yang optimal). 2. Cari kapasitas c* setiap busur pada augmenting path tersebut dengan menemukan kapasitas residual minimum dari busur pada jalur ini. Tambahkan aliran pada jalur ini sebesar c*. 3. Kurangi kapasitas residual dari setiap busur pada augmenting path ini. Tambahkan kapasitas residual sebesar c* setiap busur ini pada arah yang berlawanan dengan augmenting path tersebut. Kembali ke langkah 1. PROBLEM ALIRAN MAKSIMUM

CONTOH PROBLEM ALIRAN MAKSIMUM Bayangkan Jaringan berikut, dimana 0 adalah sumber, dan T adalah titik terminal Tujuan, Kapasitas jaringan diberikan secara langsung pada gambar. 3 A T 1 5 7 O 2 4 B 9 4 D 5 1 C 4 E 6

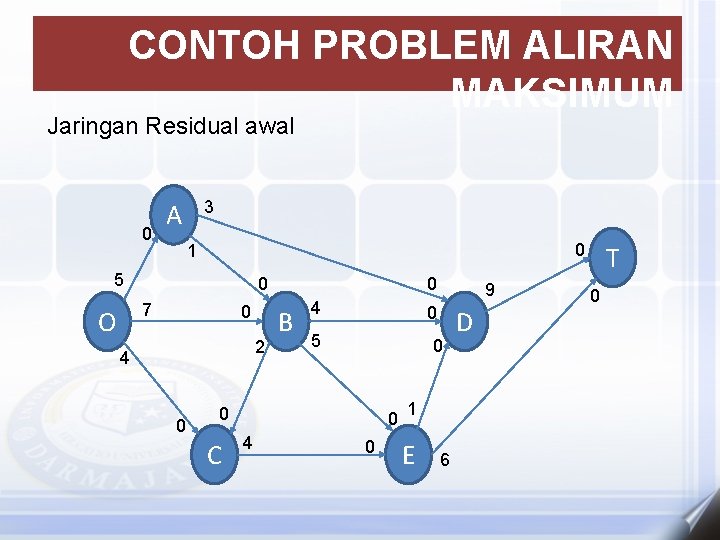
CONTOH PROBLEM ALIRAN MAKSIMUM Jaringan Residual awal 0 3 A 0 1 5 0 7 O 0 2 4 0 0 B 4 0 5 0 0 C 0 4 9 0 1 E 6 D T 0

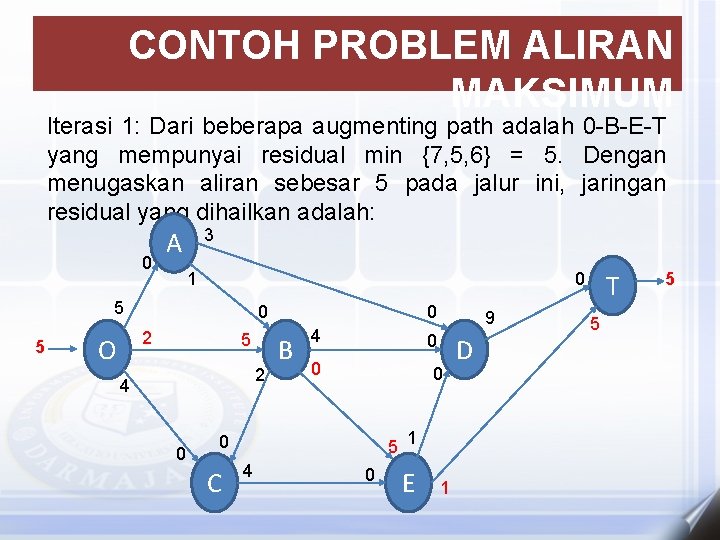
CONTOH PROBLEM ALIRAN MAKSIMUM Iterasi 1: Dari beberapa augmenting path adalah 0 -B-E-T yang mempunyai residual min {7, 5, 6} = 5. Dengan menugaskan aliran sebesar 5 pada jalur ini, jaringan residual yang dihailkan adalah: 0 3 A 0 1 5 5 0 2 O 5 2 4 0 0 B 4 0 0 C 5 4 9 0 1 E 1 D T 5 5

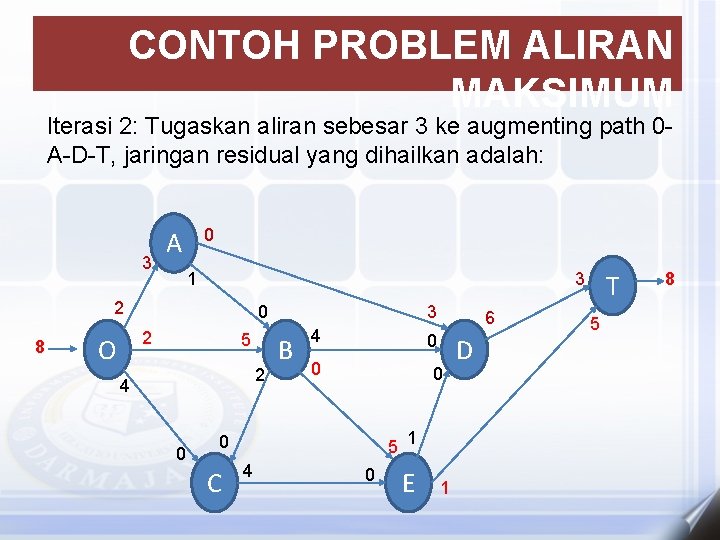
CONTOH PROBLEM ALIRAN MAKSIMUM Iterasi 2: Tugaskan aliran sebesar 3 ke augmenting path 0 A-D-T, jaringan residual yang dihailkan adalah: 3 0 A 3 1 2 8 0 2 O 5 2 4 0 3 B 4 0 0 C 5 4 6 0 1 E 1 D T 5 8

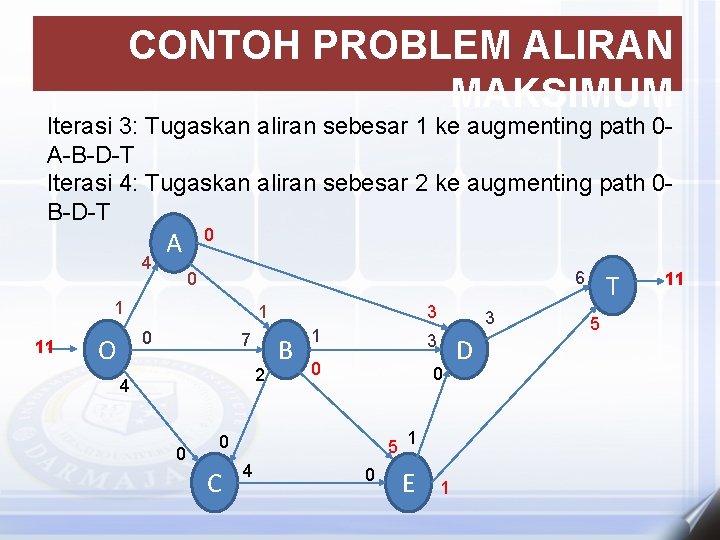
CONTOH PROBLEM ALIRAN MAKSIMUM Iterasi 3: Tugaskan aliran sebesar 1 ke augmenting path 0 A-B-D-T Iterasi 4: Tugaskan aliran sebesar 2 ke augmenting path 0 B-D-T 4 0 A 6 0 1 11 1 0 O 7 2 4 0 3 B 1 3 0 0 0 C 5 4 3 0 1 E 1 D T 5 11

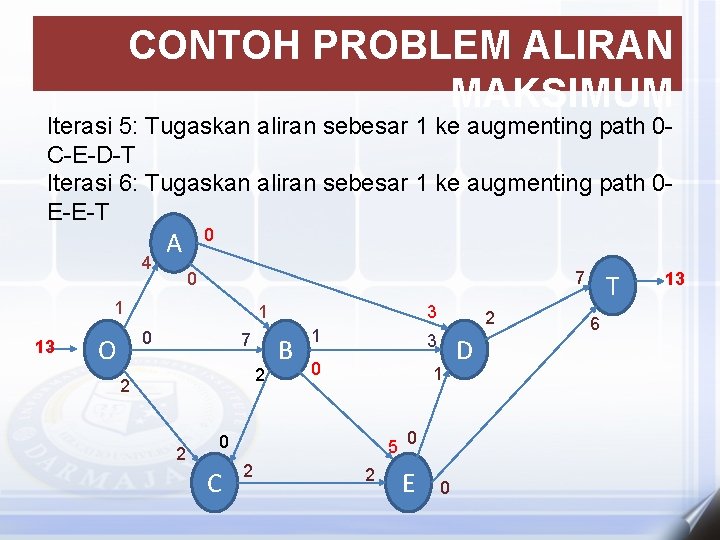
CONTOH PROBLEM ALIRAN MAKSIMUM Iterasi 5: Tugaskan aliran sebesar 1 ke augmenting path 0 C-E-D-T Iterasi 6: Tugaskan aliran sebesar 1 ke augmenting path 0 E-E-T 4 0 A 7 0 1 13 1 0 O 7 2 2 2 3 B 1 3 0 1 0 C 5 2 2 2 0 E 0 D T 6 13

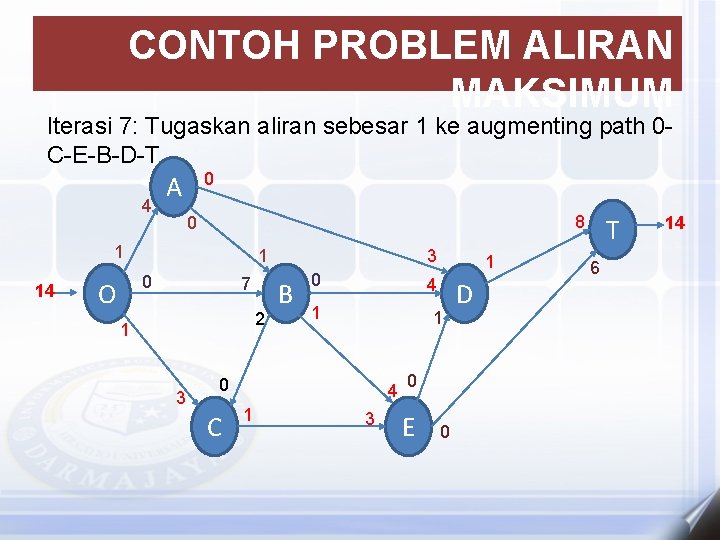
CONTOH PROBLEM ALIRAN MAKSIMUM Iterasi 7: Tugaskan aliran sebesar 1 ke augmenting path 0 C-E-B-D-T 4 0 A 8 0 1 14 1 0 O 7 2 1 3 3 B 0 4 1 1 0 C 4 1 1 3 0 E 0 D T 6 14