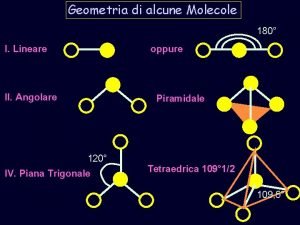
Riprendiamo alcune nozioni di geometria propedeutiche per la

Riprendiamo alcune nozioni di geometria propedeutiche per la fisica.

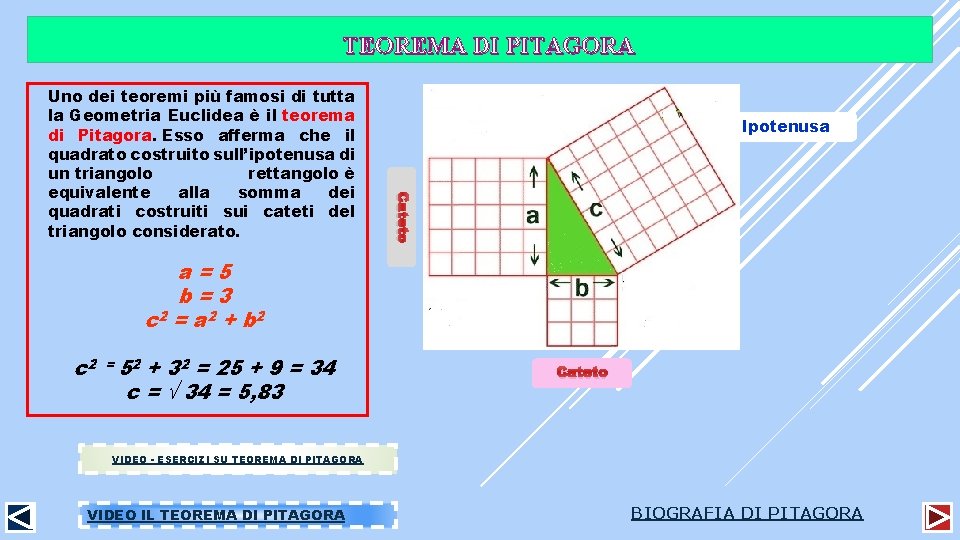
TEOREMA DI PITAGORA Ipotenusa Cateto Uno dei teoremi più famosi di tutta la Geometria Euclidea è il teorema di Pitagora. Esso afferma che il quadrato costruito sull’ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti del triangolo considerato. a=5 b=3 c 2 = a 2 + b 2 c 2 = 52 + 32 = 25 + 9 = 34 c = 34 = 5, 83 Cateto VIDEO - ESERCIZI SU TEOREMA DI PITAGORA VIDEO IL TEOREMA DI PITAGORA BIOGRAFIA DI PITAGORA

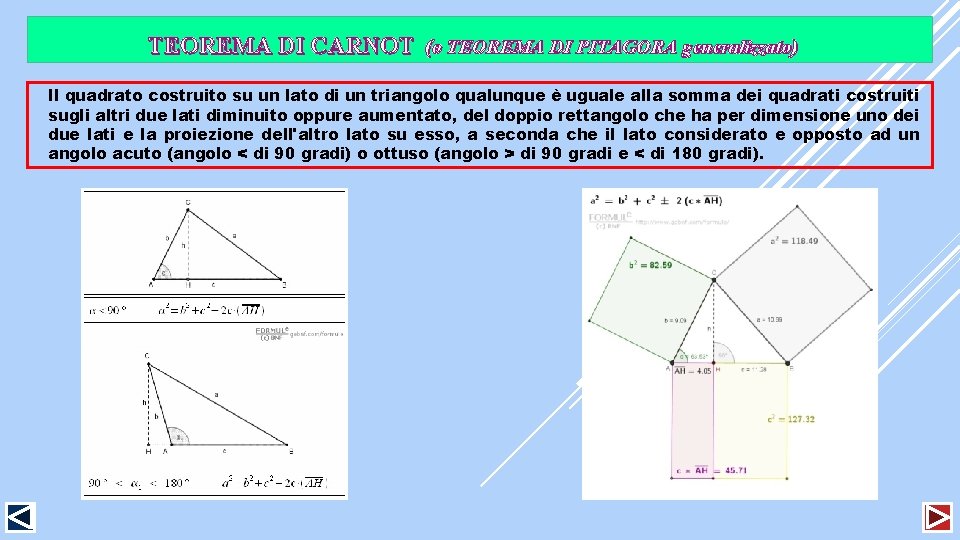
TEOREMA DI CARNOT (o TEOREMA DI PITAGORA generalizzato) Il quadrato costruito su un lato di un triangolo qualunque è uguale alla somma dei quadrati costruiti sugli altri due lati diminuito oppure aumentato, del doppio rettangolo che ha per dimensione uno dei due lati e la proiezione dell'altro lato su esso, a seconda che il lato considerato e opposto ad un angolo acuto (angolo < di 90 gradi) o ottuso (angolo > di 90 gradi e < di 180 gradi).

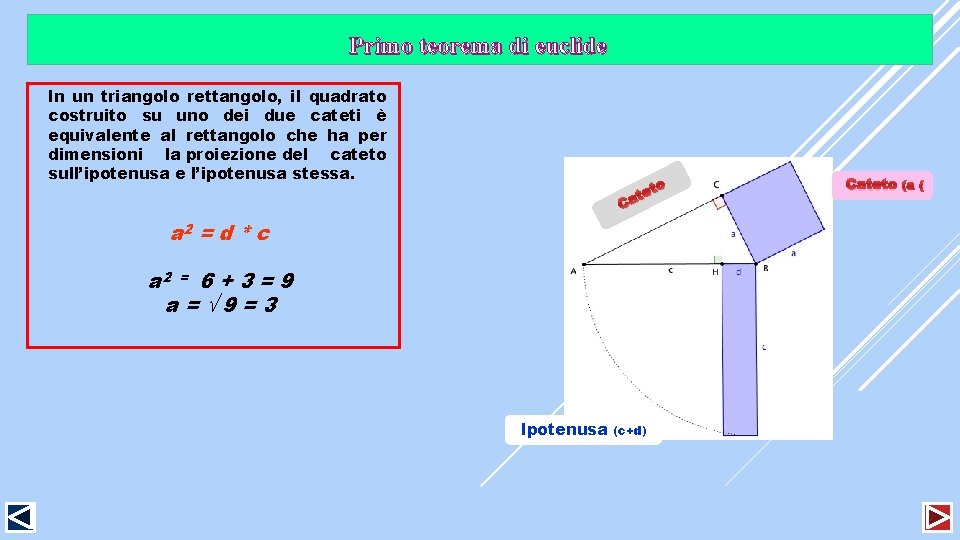
Primo teorema di euclide In un triangolo rettangolo, il quadrato costruito su uno dei due cateti è equivalente al rettangolo che ha per dimensioni la proiezione del cateto sull’ipotenusa e l’ipotenusa stessa. to e at C a 2 = d * c a 2 = 6 + 3 = 9 a= 9=3 Ipotenusa (c+d) Cateto

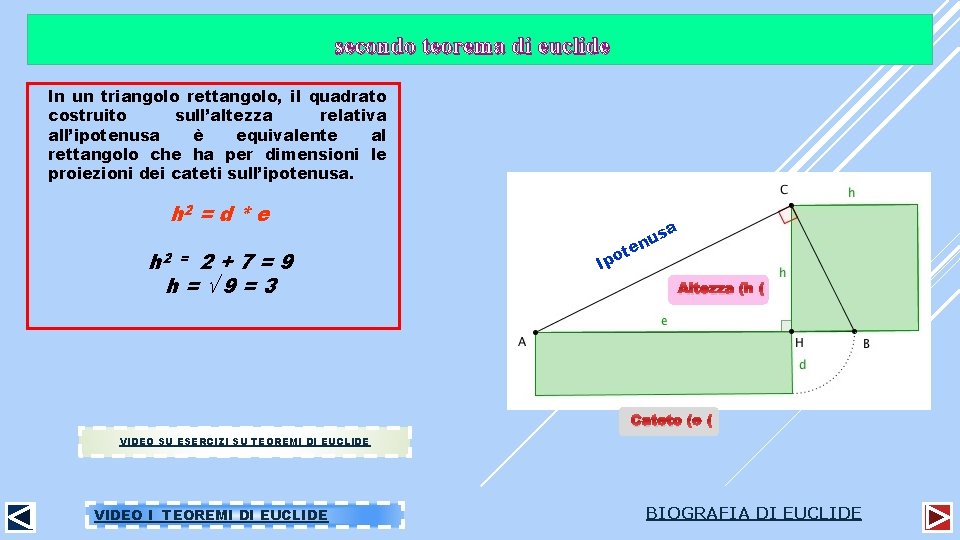
secondo teorema di euclide In un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa. h 2 = d * e h 2 = 2+7=9 h= 9=3 te Ipo a s nu Altezza Cateto VIDEO SU ESERCIZI SU TEOREMI DI EUCLIDE VIDEO I TEOREMI DI EUCLIDE BIOGRAFIA DI EUCLIDE

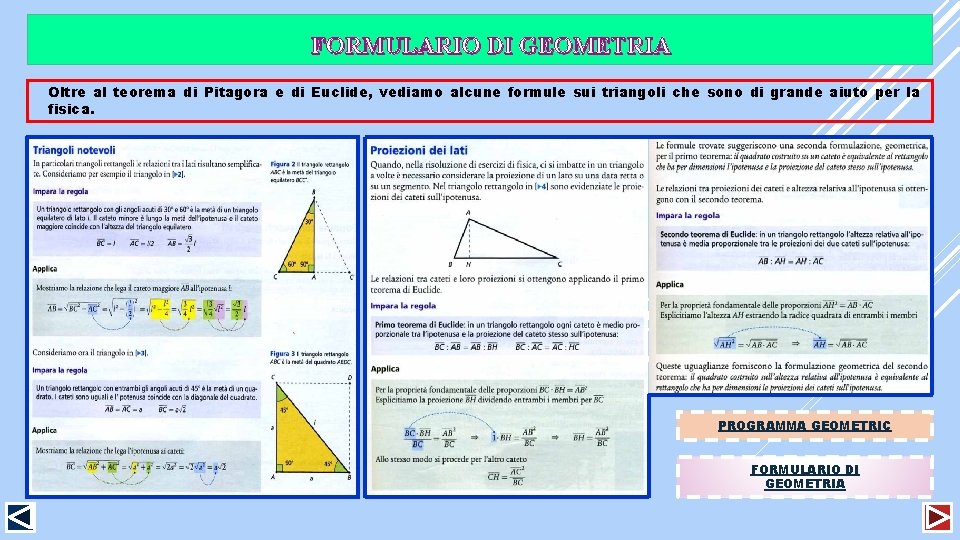
FORMULARIO DI GEOMETRIA Oltre al teorema di Pitagora e di Euclide, vediamo alcune formule sui triangoli che sono di grande aiuto per la fisica. PROGRAMMA GEOMETRIC FORMULARIO DI GEOMETRIA

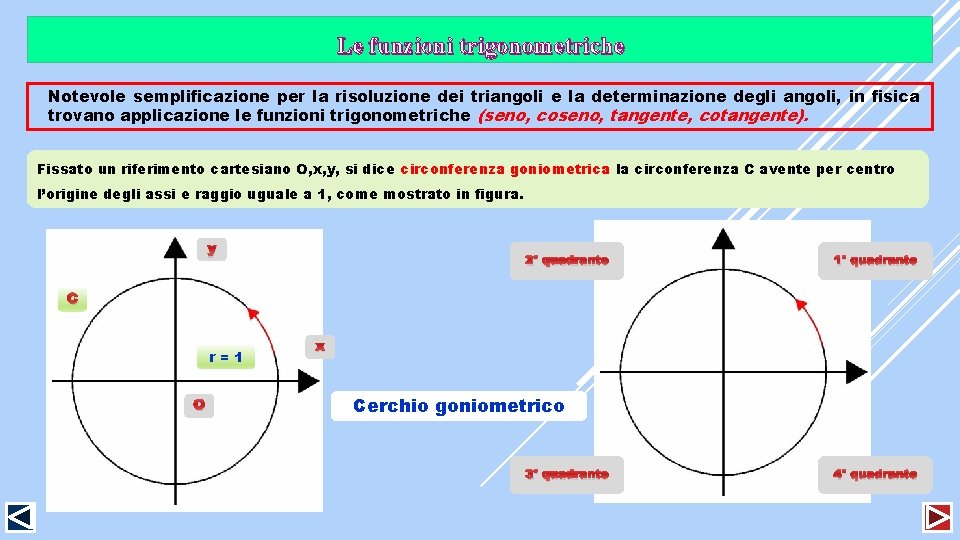
Le funzioni trigonometriche Notevole semplificazione per la risoluzione dei triangoli e la determinazione degli angoli, in fisica trovano applicazione le funzioni trigonometriche (seno, coseno, tangente, cotangente). Fissato un riferimento cartesiano O, x, y, si dice circonferenza goniometrica la circonferenza C avente per centro l’origine degli assi e raggio uguale a 1, come mostrato in figura. y 2° quadrante 1° quadrante C r=1 O x Cerchio goniometrico 3° quadrante 4° quadrante

Partiamo dal definire la funzione seno e coseno. Consideriamo un angolo sulla circonferenza goniometrica. L'angolo in questione può essere espresso sia in gradi che in radianti, poco importa. Chiamiamo P il punto intercettato dall'angolo sulla circonferenza, e Q ed R le proiezioni di questo punto rispettivamente sull'asse y e sull'asse x. Dato il triangolo rettangolo ORP : v si dice seno dell'angolo α il rapporto tra il cateto opposto all'angolo e l'ipotenusa del triangolo. In simboli : v si dice coseno dell'angolo α il rapporto tra il cateto adiacente all'angolo e l'ipotenusa del triangolo. In simboli : ricordando che abbiamo scelto una circonferenza goniometrica di raggio 1, risulta quindi : OP = 1,

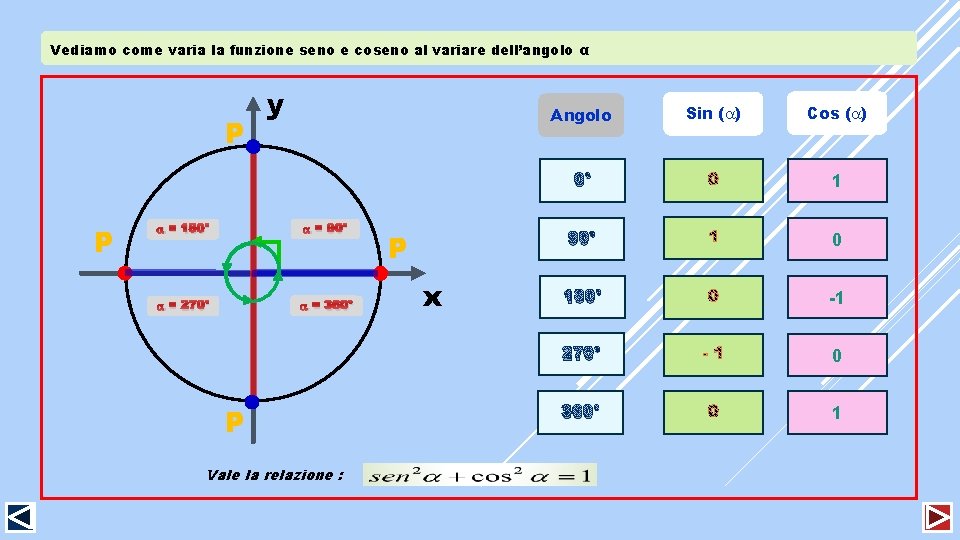
Vediamo come varia la funzione seno e coseno al variare dell’angolo α P P y Angolo = 180° = 90° = 270° 0° ==360° P Vale la relazione : P x Sin ( ) Cos ( ) 0° 1 90° 0 180° -1 270° 0 360° 1

Definiamo brevemente la funzione tangente e cotangente. Consideriamo sempre un angolo sulla circonferenza goniometrica. La tangente dell'angolo α è l’ordinata del punto dall’intersezione della semiretta rappresentante il lato libero dell’angolo con la retta tangente alla circonferenza nel punto (1, 0). In sostanza la tangente è l’ordinata del punto T. Ricordate che la circonferenza goniometrica ha raggio unitario, quindi : Dunque, in riferimento all’immagine : La tangente dell'angolo α è definita anche : La cotangente dell'angolo α è definita come il reciproco della tangente del medesimo angolo :

A che servono i teoremi di trigonometria sui triangoli rettangoli? E’ la prima domanda che probabilmente vi passa per la testa. La prima risposta che possiamo dare è che queste formule hanno notevoli conseguenze geometriche e quindi «fisiche» ! Se è la prima volta che incontrate questi argomenti, diciamo che la loro ci permettono di risolvere i triangoli rettangoli, cioè ci permettono di determinare a partire da almeno due elementi dati (angolo-cateto, cateto-ipotenusa) tutte le altre caratteristiche del triangolo (cateti, ipotenusa, angoli).

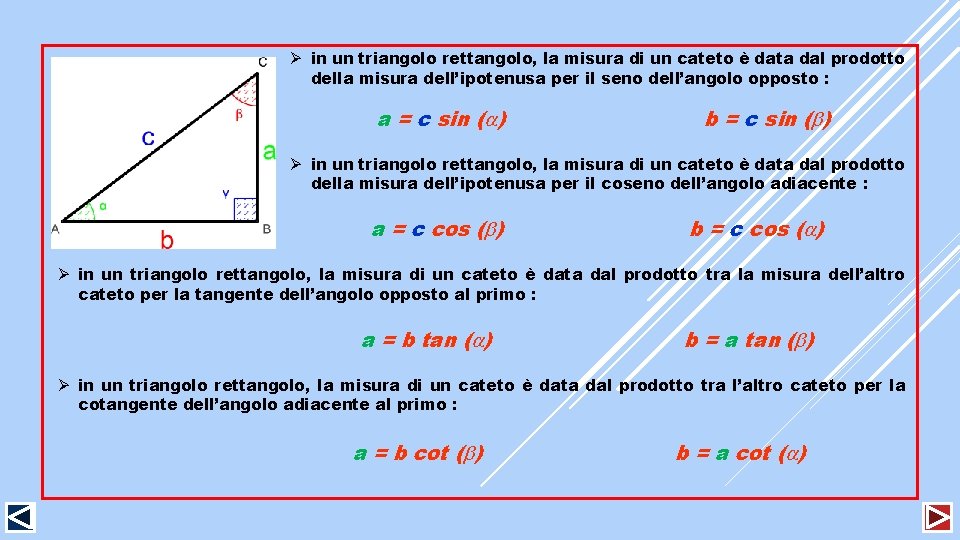
Ø in un triangolo rettangolo, la misura di un cateto è data dal prodotto della misura dell’ipotenusa per il seno dell’angolo opposto : a = c sin ( ) b = c sin ( ) Ø in un triangolo rettangolo, la misura di un cateto è data dal prodotto della misura dell’ipotenusa per il coseno dell’angolo adiacente : a = c cos ( ) b = c cos ( ) Ø in un triangolo rettangolo, la misura di un cateto è data dal prodotto tra la misura dell’altro cateto per la tangente dell’angolo opposto al primo : a = b tan ( ) b = a tan ( ) Ø in un triangolo rettangolo, la misura di un cateto è data dal prodotto tra l’altro cateto per la cotangente dell’angolo adiacente al primo : a = b cot ( ) b = a cot ( )

Esempio : C = 3 m e = 30 ° si ottiene : a = C * sin ( ) = 5 * sin ( 30° ) = 5 * 0, 50 = 2, 5 m b = C * cos ( ) = 5 * cos ( 30° ) = 5 * 0, 86 = 4, 3 m C = 3 m e = 60 ° si ottiene : a = C * cos ( ) = 5 * cos ( 60° ) = 5 * 0, 50 = 2, 5 m b = 4, 3 m e = 30 ° si ottiene : b = C * sin ( ) = 5 * sin ( 60° ) = 5 * 0, 86 = 4, 3 m a = b * tan ( ) = 4, 3 * tan ( 30° ) = 4, 3 * 0, 58 = 2, 5 m b = 4, 3 m e = 60 ° si ottiene : a = b * cot ( ) = 4, 3 * cot ( 60° ) = 4, 3 * 0, 58 = 2, 5 m

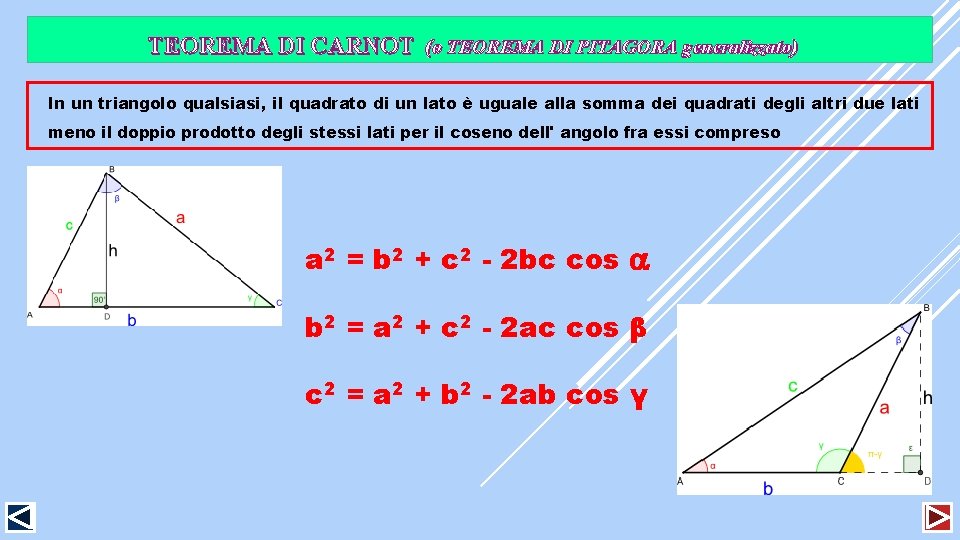
TEOREMA DI CARNOT (o TEOREMA DI PITAGORA generalizzato) In un triangolo qualsiasi, il quadrato di un lato è uguale alla somma dei quadrati degli altri due lati meno il doppio prodotto degli stessi lati per il coseno dell' angolo fra essi compreso a 2 = b 2 + c 2 - 2 bc cos b 2 = a 2 + c 2 - 2 ac cos β c 2 = a 2 + b 2 - 2 ab cos γ

Definizione e trasformazione degli angoli Un angolo può misurarsi in : - gradi sessagesimali; - gradi centesimali; - radianti v Un grado sessagesimale è la trecentosessantesima parte di un angolo giro (°). Un grado è a sua volta diviso in sessanta parti ed ogni parte si chiama minuto. Un minuto è a sua volta diviso in sessanta parti ed ogni parte si chiama secondo. Esempio : 22° 19’ 25’’. v Un grado centesimale (gon) è la quattrocentesima parte di un angolo giro (g). Un grado centesimale è a sua volta diviso in cento parti ed ogni parte si chiama minuto centesimale. Un minuto centesimale è a sua volta diviso in cento parti ed ogni parte si chiama secondo centesimale. Esempio : 122 g, 1975. v Il radiante (rad) è l’angolo sotteso da un arco di lunghezza pari al raggio. Esempio : 1, 5 .

Per meglio capire gli angoli in radiante si può far riferimento a quanto segue : Consideriamo il cerchio goniometrico di R = 1 Tagliamo la circonferenza e la srotoliamo su di un piano osserviamo che essa è lunga 6, 28 volte il raggio. 1 2 3 4 5 6 0, 28 Quindi metà circonferenza corrisponde a 3, 14 volte il raggio. Fissato come numero fisso corrispondente all’angolo piatto di 180°. Di conseguenza la circonferenza di un cerchio vale proprio C = 2 R. per R = 1 C = 2 * 3, 14 * 1 = 6, 28 per R = 2 C = 2 * 3, 14 * 2 = 12, 56 per R = 3 C = 2 * 3, 14 * 3 = 18, 84 ………… ecc.

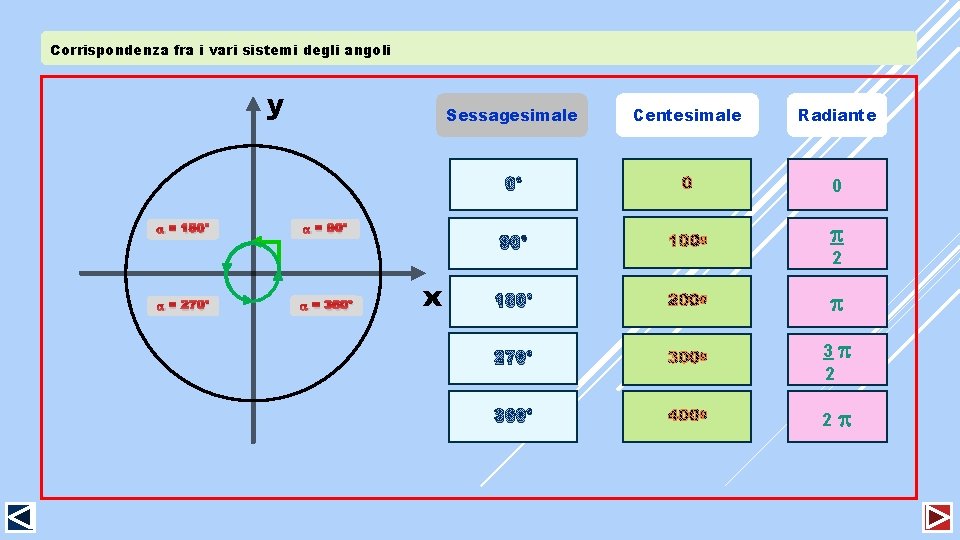
Corrispondenza fra i vari sistemi degli angoli y = 180° = 270° Sessagesimale = 90° 0° ==360° x Centesimale Radiante 0° 0 90° 180° 270° 3 2 360° 2 2

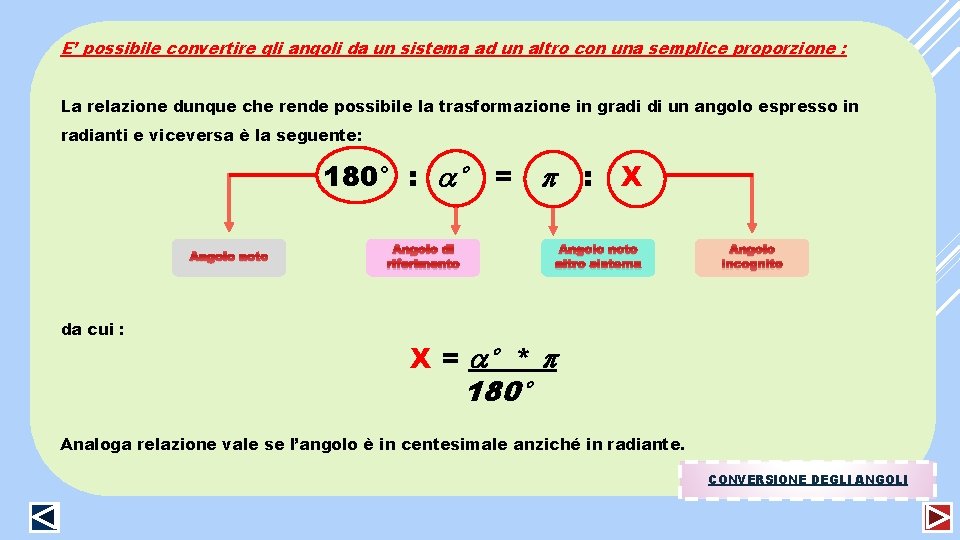
E’ possibile convertire gli angoli da un sistema ad un altro con una semplice proporzione : La relazione dunque che rende possibile la trasformazione in gradi di un angolo espresso in radianti e viceversa è la seguente: 180° : ° Angolo noto da cui : = Angolo di riferimento : X Angolo noto altro sistema Angolo incognito X = ° * 180° Analoga relazione vale se l’angolo è in centesimale anziché in radiante. CONVERSIONE DEGLI ANGOLI

Esempio : Calcolare la misura in radianti dell’angolo 50° 180° : 50 = : X X = (50 * ) / 180° = 0, 87 Calcolare la misura in gradi centesimali dell’angolo 60° 180° : 60 = 200 g : X X = (60 * 200) / 180° = 66, 7 Calcolare la misura in gradi dell’angolo (3/2) : (3/2) = 180° : X X = [180° * (3/2) ] / = 270°

GRAFICO DI SENO E COSENO AL VARIARE DELL’ANGOLO RAPPRESENTAZIONI CON IL PROGRAMMA GEOGEBRA ROMBO PARALLELOGRAMMA TRAPEZIO

VIDEO LE EQUAZIONI DI PRIMO GRADO VIDEO INTEGRATIVO SULLE PROPROZIONI VIDEO INTEGRATIVO SULLE PERCENTUALI Videi integrativi di schooltoon VIDEO IL PUNTO, LA RETTA E IL PIANO VIDEO SENO E COSENO, TRIGONOMETRIA VIDEO IL TEOREMA DI PITAGORA VIDEO ESERCIZI SUL TEOREMA DI PITAGORA VIDEO I TEOREMI DI EUCLIDE

ESERCITAZIONE SULLE FORMULE DIRETTE ESERCITAZIONE SULLE PERCENTUALI ESERCITAZIONE SULLE FORMULE INVERSE ESERCITAZIONE SULLE POTENZE ESERCITAZIONE SULLE PROPORZIONI Esercitiamoci su quanto trattato ESERCITAZIONE SUI TRIANGOLI ESERCITAZIONE SULLE FUNZIONI TRIGONOMETRICHE