Right Triangle Trigonometry Section 6 5 Pythagorean Theorem






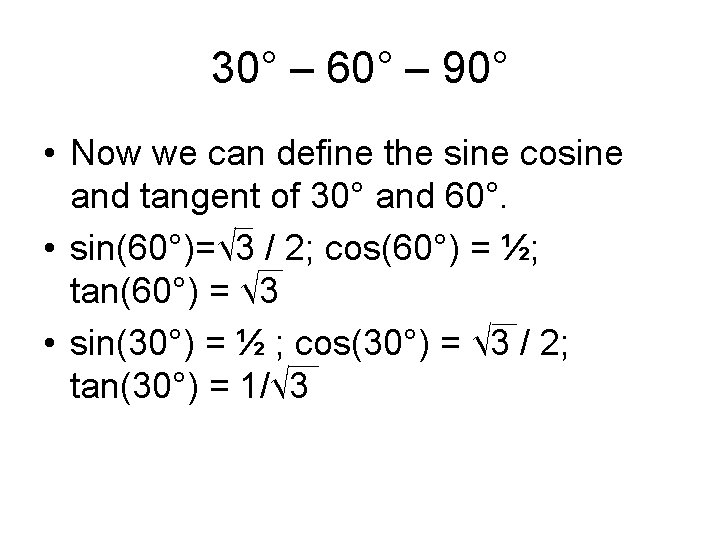






- Slides: 16

Right Triangle Trigonometry Section 6. 5

Pythagorean Theorem • Recall that a right triangle has a 90° angle as one of its angles. • The side that is opposite the 90° angle is called the hypotenuse. • The theorem due to Pythagoras says that the square of the hypotenuse is equal to the sum of the squares of the legs. c 2 = a 2 + b 2 a c b

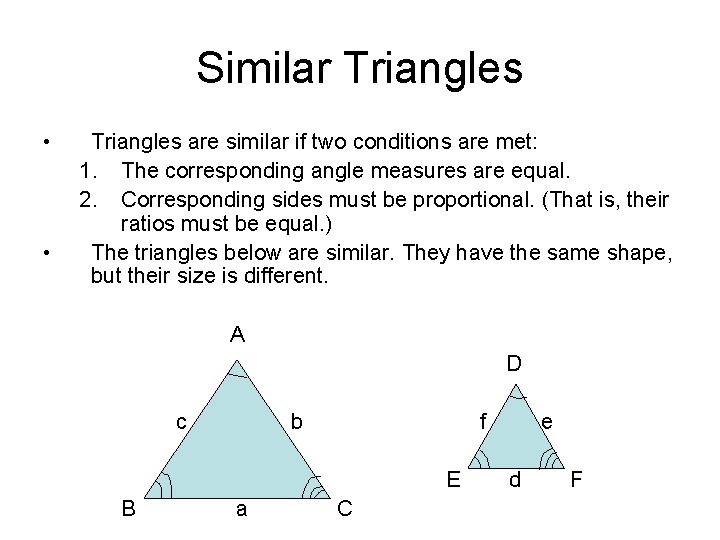
Similar Triangles • • Triangles are similar if two conditions are met: 1. The corresponding angle measures are equal. 2. Corresponding sides must be proportional. (That is, their ratios must be equal. ) The triangles below are similar. They have the same shape, but their size is different. A D c b f E B a C e d F

Corresponding angles and sides • As you can see from the previous page we can see that angle A is equal to angle D, angle B equals angle E, and angle C equals angle F. • The lengths of the sides are different but there is a correspondence. Side a is in correspondence with side d. Side b corresponds to side e. Side c corresponds to side f. • What we do have is a set of proportions. • a/d = b/e = c/f

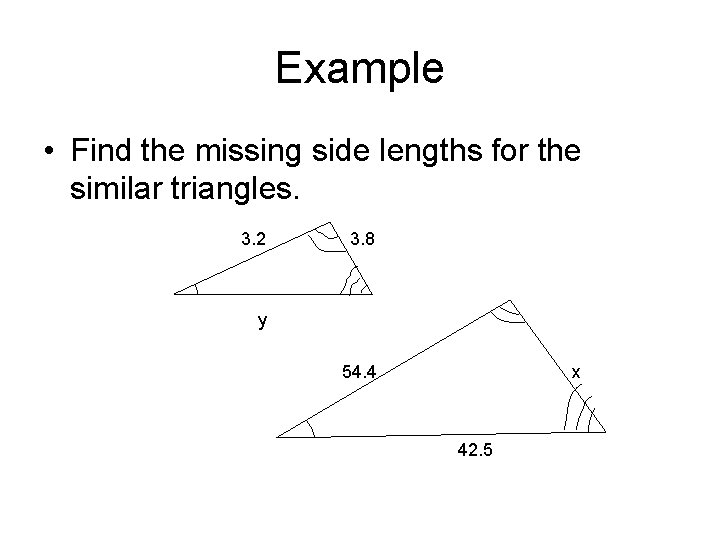
Example • Find the missing side lengths for the similar triangles. 3. 2 3. 8 y 54. 4 x 42. 5

ANSWER • Notice that the 54. 4 length side corresponds to the 3. 2 length side. This will form are complete ratio. • To find x, we notice side x corresponds to the side of length 3. 8. • Thus we have 3. 2/54. 4 = 3. 8/x. Solve for x. • Thus x = (54. 4)(3. 8)/3. 2 = 64. 6 • Same thing for y we see that 3. 2/54. 4 = y/42. 5. Solving for y gives y = (42. 5)(3. 2)/54. 4 = 2. 5.

Introduction to Trigonometry • In this section we define three basic trigonometric ratios, sine, cosine and tangent. • opp is the side opposite angle A • adj is the side adjacent to angle A • hyp is the hypotenuse of the right triangle hyp opp adj A

Definitions • Sine is abbreviated sin, cosine is abbreviated cos and tangent is abbreviated tan. • The sin(A) = opp/hyp • The cos(A) = adj/hyp • The tan(A) = opp/adj • Just remember sohcahtoa! • Sin Opp Hyp Cos Adj Hyp Tan Opp Adj

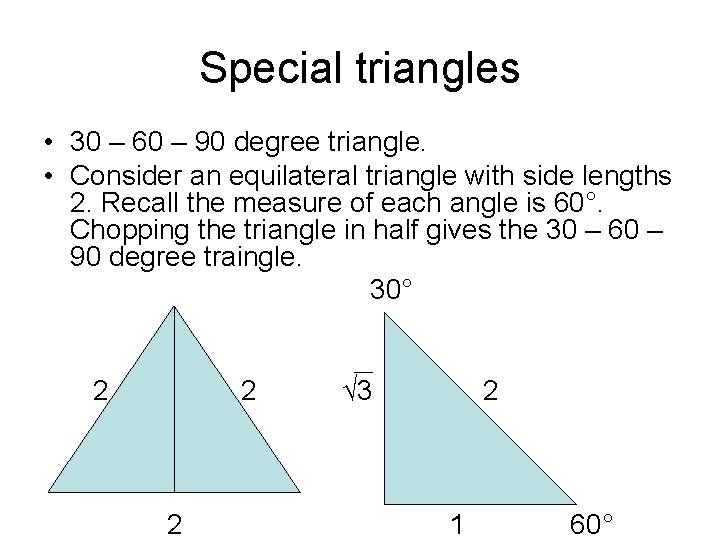
Special triangles • 30 – 60 – 90 degree triangle. • Consider an equilateral triangle with side lengths 2. Recall the measure of each angle is 60°. Chopping the triangle in half gives the 30 – 60 – 90 degree traingle. 30° 2 2 2 √ 3 2 1 60°
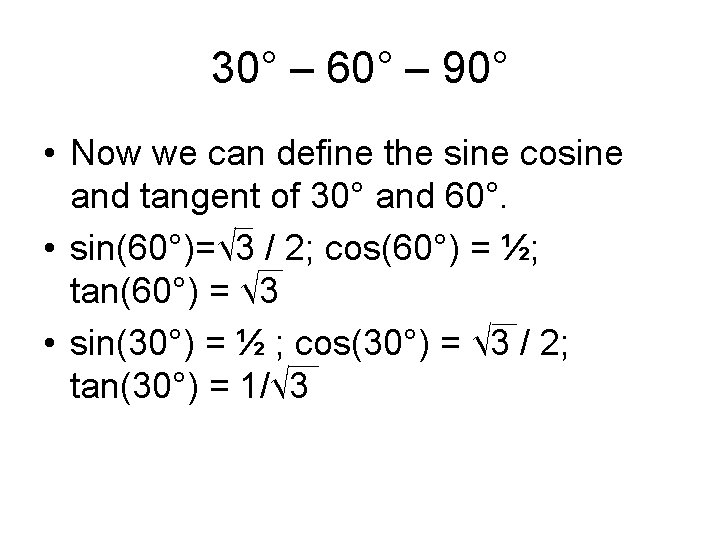
30° – 60° – 90° • Now we can define the sine cosine and tangent of 30° and 60°. • sin(60°)=√ 3 / 2; cos(60°) = ½; tan(60°) = √ 3 • sin(30°) = ½ ; cos(30°) = √ 3 / 2; tan(30°) = 1/√ 3

45° – 90° • Consider a right triangle in which the lengths of each leg are 1. This implies the hypotenuse is √ 2. 45° sin(45°) = 1/√ 2 cos(45°) = 1/√ 2 1 tan(45°) = 1 1 45°

Example • Find the missing side lengths and angles. 60° A = 180°-90°-60°=30° sin(60°)=y/10 10 x thus y=10 sin(60°) A y

Inverse Trig Functions • What if you know all the sides of a right triangle but you don’t know the other 2 angle measures. How could you find these angle measures? • What you need is the inverse trigonometric functions. • Think of the angle measure as a present. When you take the sine, cosine, or tangent of that angle, it is similar to wrapping your present. • The inverse trig functions give you the ability to unwrap your present and to find the value of the angle in question.

Notation • A=sin-1(z) is read as the inverse sine of A. • Never think of the -1 as an exponent. It may look like an exponent and thus you might think it is 1/sin(z), this is not true. • (We refer to 1/sin(z) as the cosecant of z) • A=cos-1(z) is read as the inverse cosine of A. • A=tan-1(z) is read as the inverse tangent of A.

Inverse Trig definitions • Referring to the right triangle from the introduction slide. The inverse trig functions are defined as follows: • A=sin-1(opp/hyp) • A=cos-1(adj/hyp) • A=tan-1(opp/adj)

Example using inverse trig functions • Find the angles A and B given the following right triangle. • Find angle A. Use an inverse trig function to find A. For instance A=sin-1(6/10)=36. 9°. • Then B = 180° - 90° - 36. 9° = 53. 1°. B 6 10 8 A