Right minus left What is the volume if









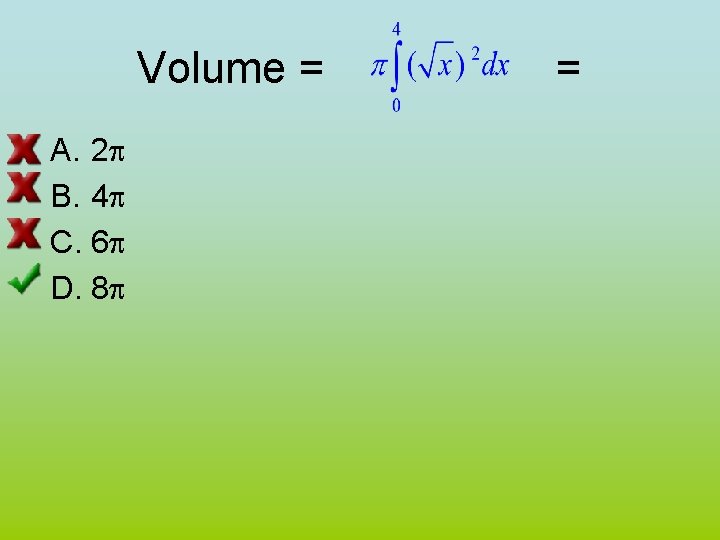

![Revolve the shown area about the x-axis. A. ] B. ] C. ] Revolve the shown area about the x-axis. A. ] B. ] C. ]](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-20.jpg)
![Revolve the shown area about the x-axis. A. ] B. ] C. ] Revolve the shown area about the x-axis. A. ] B. ] C. ]](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-21.jpg)
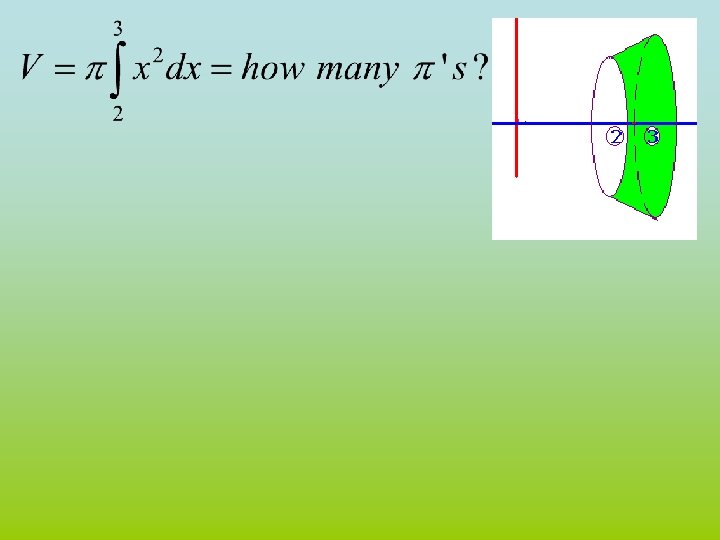
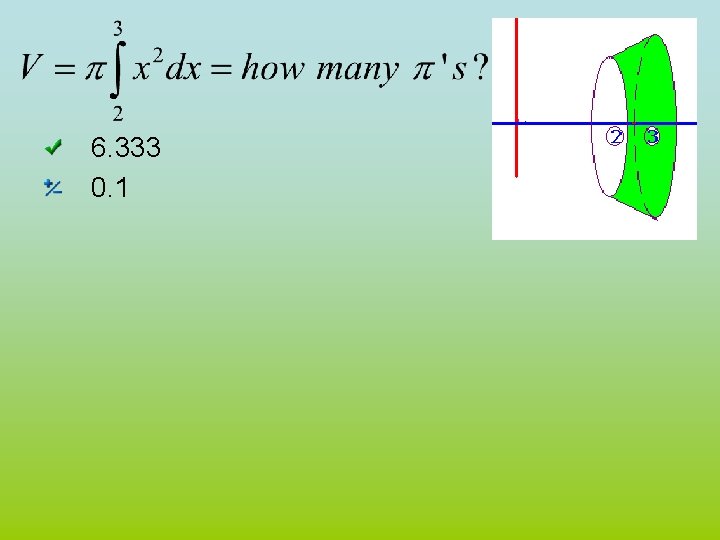




![Volume = = p[(7 -5)/35] = 2 p /35 Volume = = p[(7 -5)/35] = 2 p /35](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-28.jpg)
![Find the volume A. [] B. [] C. [] Find the volume A. [] B. [] C. []](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-29.jpg)
![Find the volume A. [] B. [] C. [] Find the volume A. [] B. [] C. []](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-30.jpg)




![] 9. 83 0. 2 ] 9. 83 0. 2](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-36.jpg)

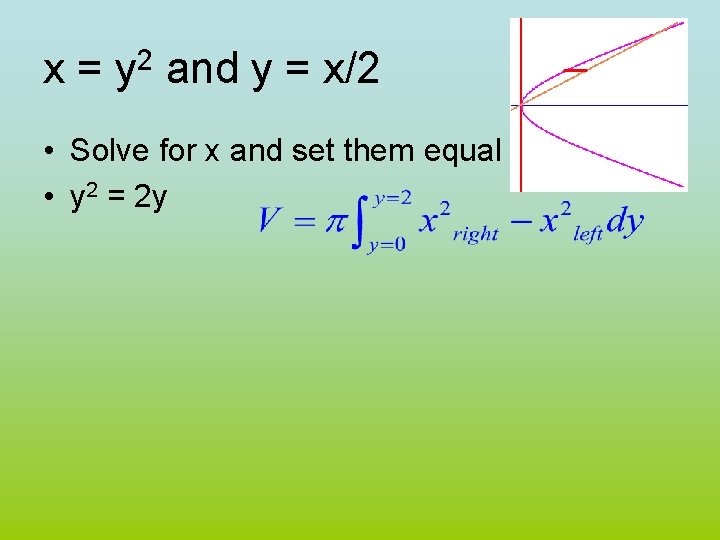
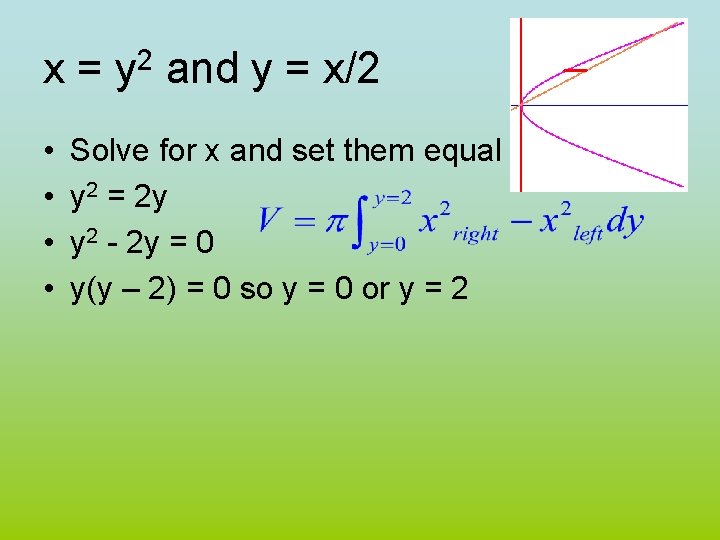
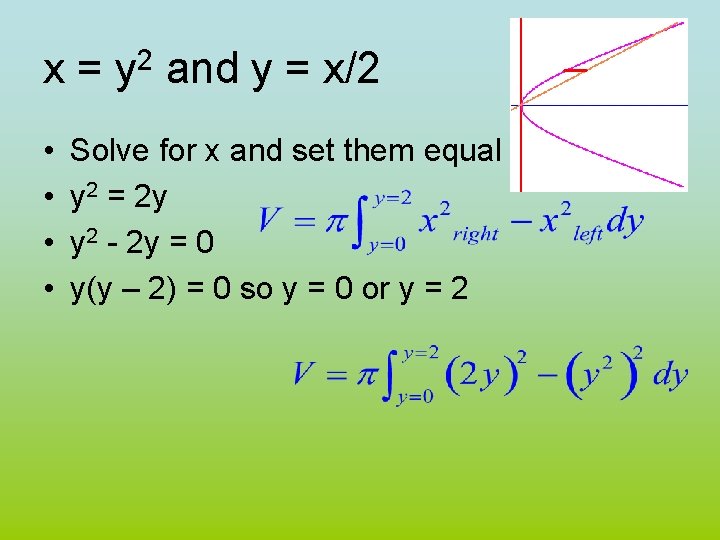

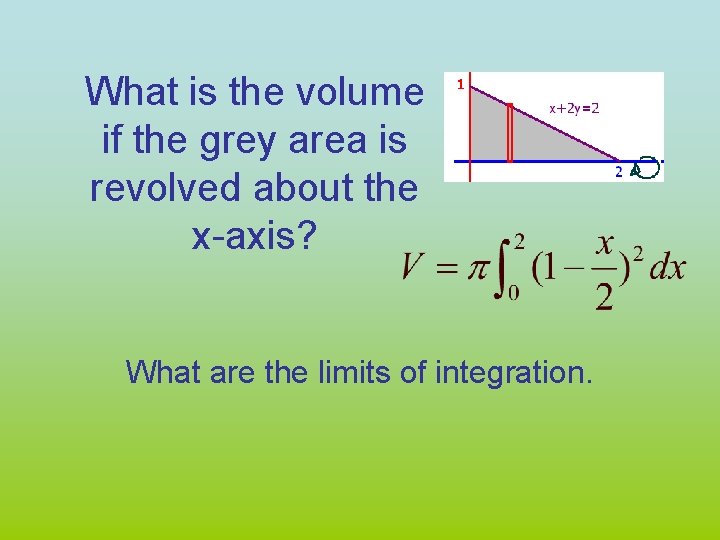
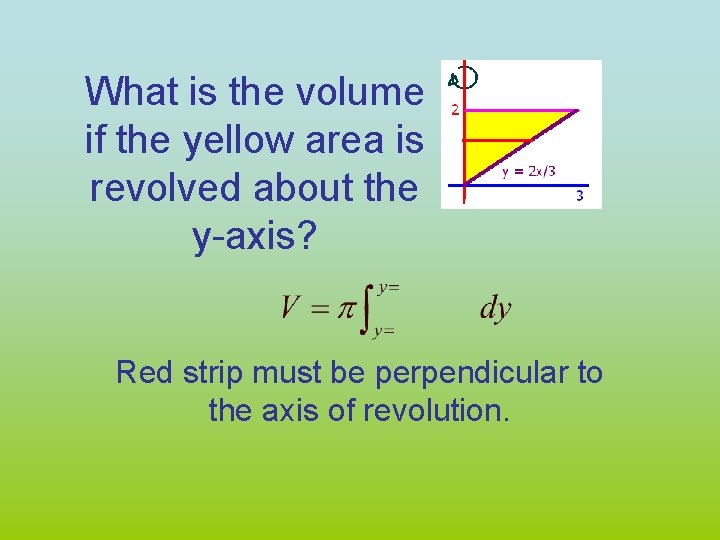
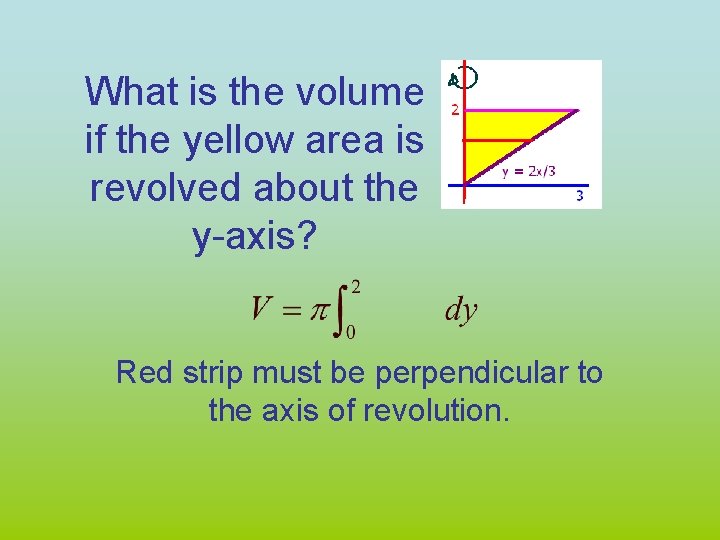

![=-p/3[0 -1] =-p/3[0 -1]](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-47.jpg)


![A. B. C. First two places y=cosx and y=2 sinxcosx cross? ] x= p/3, A. B. C. First two places y=cosx and y=2 sinxcosx cross? ] x= p/3,](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-54.jpg)


![] 0. 25 0. 1 ] 0. 25 0. 1](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-57.jpg)
- Slides: 57

Right minus left


What is the volume if the yellow area is rotated about the x-axis?

An easier question would be an easier graph of f(x).

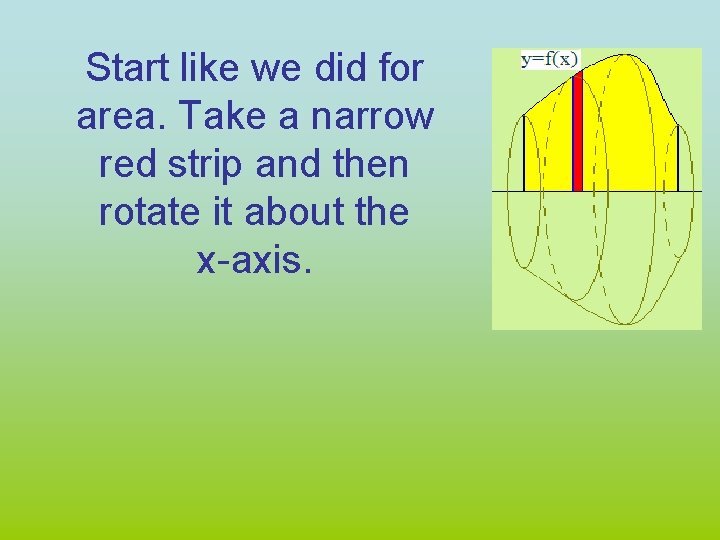
Start like we did for area. Take a narrow red strip and then rotate it about the x-axis.

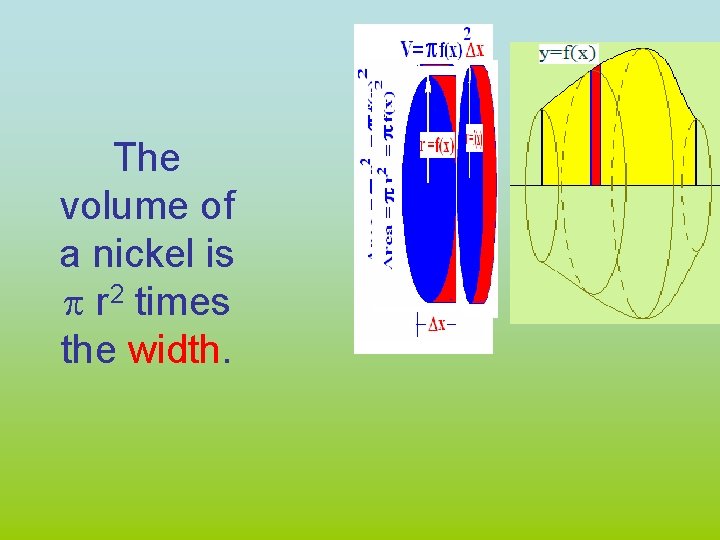
The volume of a nickel is p r 2 times the width.

Find the volume of a stool with radius 10 ft. and height 1/p ft. A. 10/p cubic feet B. 100 p cubic feet C. 10 cubic feet D. 100 cubic feet

Find the volume of a stool with radius 10 ft. and height 1/p ft. A. 10/p cubic feet B. 100 p cubic feet C. 10 cubic feet D. 100 cubic feet

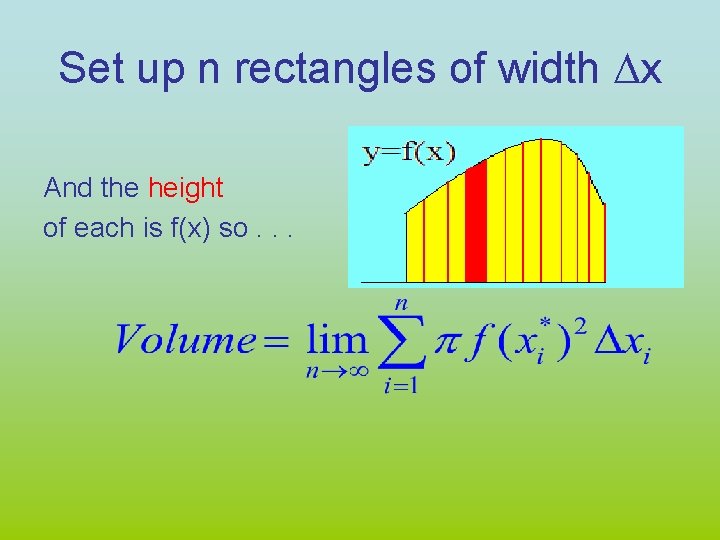
Set up n rectangles of width Dx And the height of each is f(x) so. . .

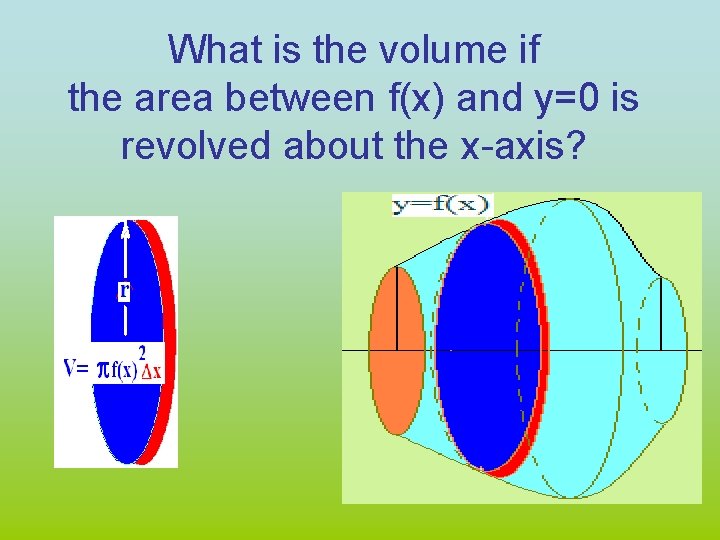
What is the volume if the area between f(x) and y=0 is revolved about the x-axis?


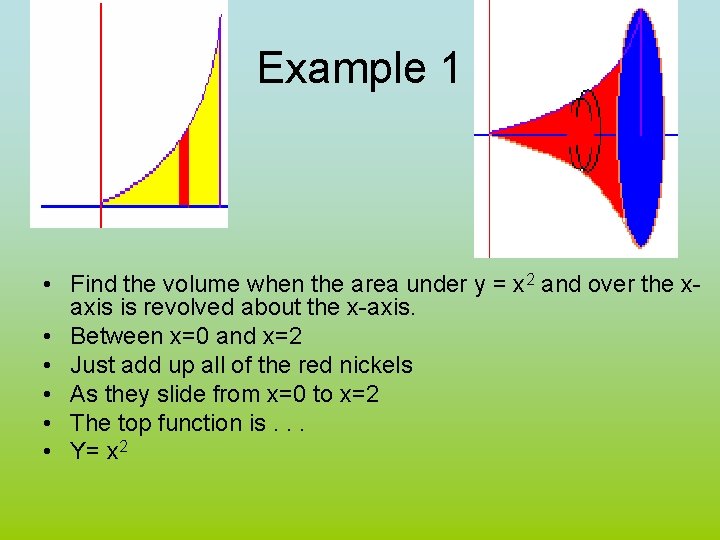
Example 1 • Find the volume when the area under y = x 2 and over the xaxis is revolved about the x-axis. • Between x=0 and x=2 • Just add up all of the red nickels • As they slide from x=0 to x=2 • The top function is. . . • Y= x 2

By the definition of the definite integral Volume =

Example 1 • Find the volume when the area under y=x 2 • Between x=0 and x=2 • Is revolved about the x-axis = p x 5/5 = p 32/5

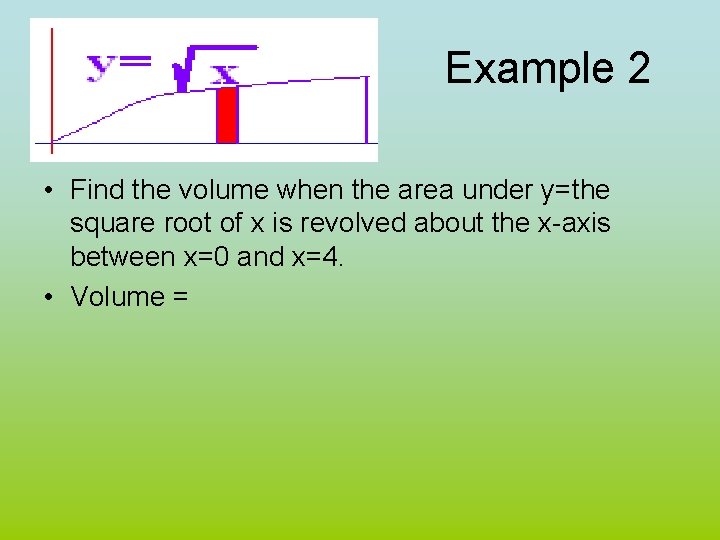
Example 2 • Find the volume when the area under y=the square root of x is revolved about the x-axis between x=0 and x=4. • Volume =

• Volume =

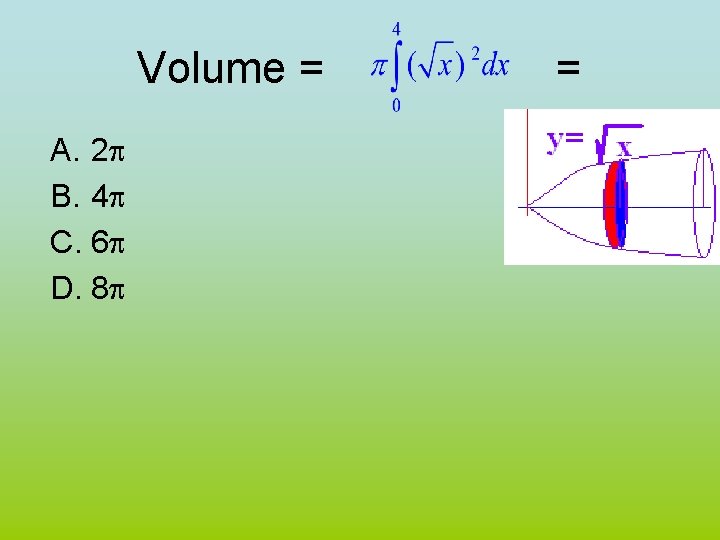
Volume = A. 2 p B. 4 p C. 6 p D. 8 p =
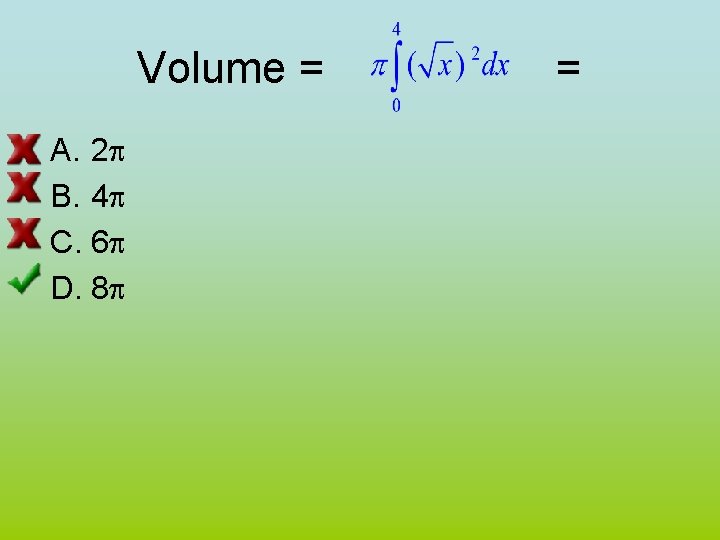
Volume = A. 2 p B. 4 p C. 6 p D. 8 p =

• Volume =
![Revolve the shown area about the xaxis A B C Revolve the shown area about the x-axis. A. ] B. ] C. ]](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-20.jpg)
Revolve the shown area about the x-axis. A. ] B. ] C. ]
![Revolve the shown area about the xaxis A B C Revolve the shown area about the x-axis. A. ] B. ] C. ]](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-21.jpg)
Revolve the shown area about the x-axis. A. ] B. ] C. ]
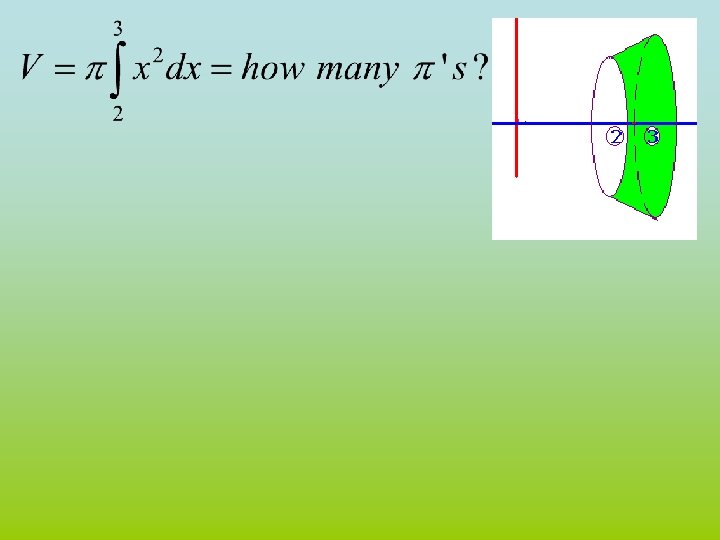
[ 6. 333 0. 1

Example 3 Washer Method • Spin the shown region about the x-axis • Show red strip perpendicular to the axis of revolution

Example 3 Washer Method • Use the disc method for the top function • Use it again for the bottom one • Subtract the two answers

Example 3 Washer Method .

Speaker Washer Method • • Set the two functons equal to each other Solve for x x 2 = x 3 or 0 = x 3 - x 2 By factoring 0 = x 2 ( x – 1 ) so x 2 =0 or x– 1=0 Next we add up all of the red washers From 0 to 1 Volume =
![Volume p7 535 2 p 35 Volume = = p[(7 -5)/35] = 2 p /35](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-28.jpg)
Volume = = p[(7 -5)/35] = 2 p /35
![Find the volume A B C Find the volume A. [] B. [] C. []](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-29.jpg)
Find the volume A. [] B. [] C. []
![Find the volume A B C Find the volume A. [] B. [] C. []](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-30.jpg)
Find the volume A. [] B. [] C. []





![9 83 0 2 ] 9. 83 0. 2](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-36.jpg)
] 9. 83 0. 2


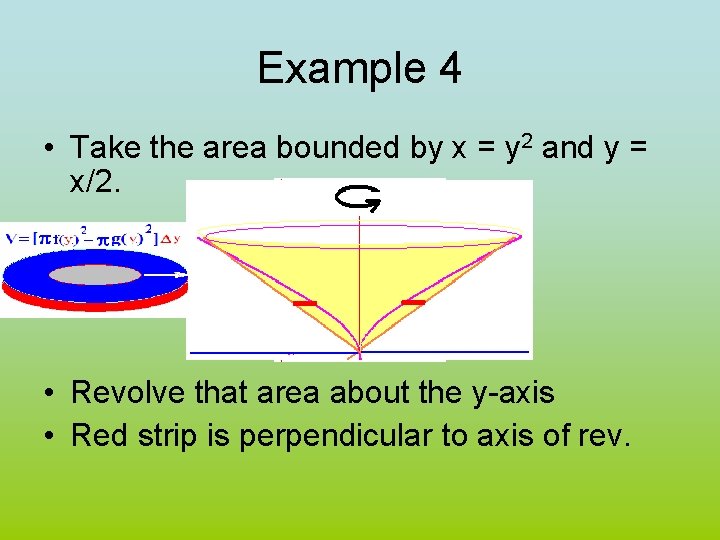
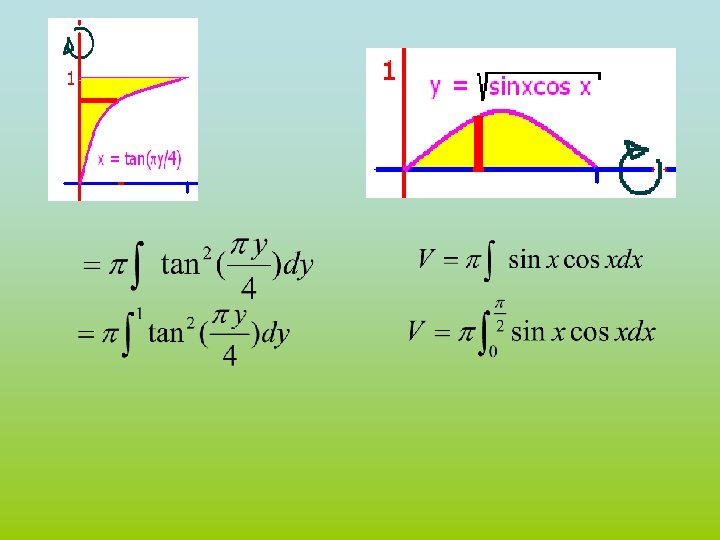
Example 4 • Take the area bounded by x = y 2 and y = x/2. • Revolve that area about the y-axis • Red strip is perpendicular to axis of rev.
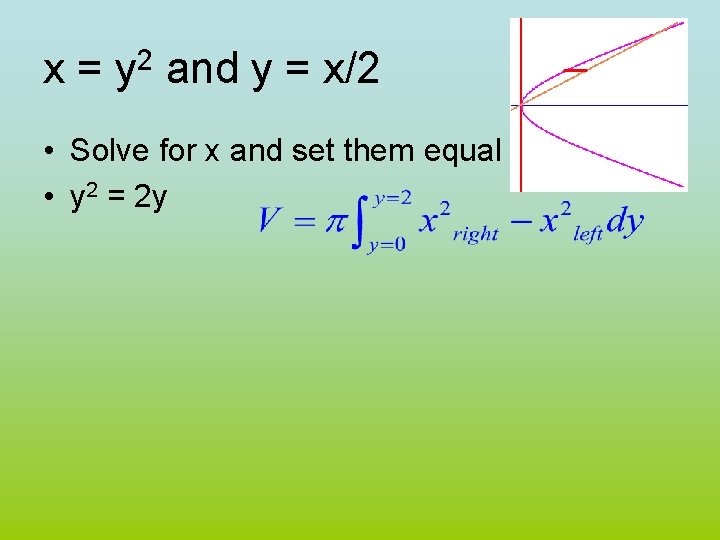
x = y 2 and y = x/2 • Solve for x and set them equal • y 2 = 2 y
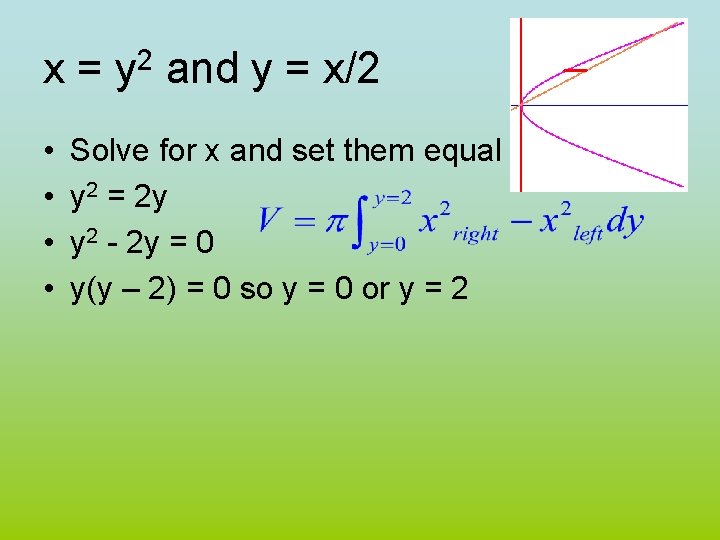
x = y 2 and y = x/2 • • Solve for x and set them equal y 2 = 2 y y 2 - 2 y = 0 y(y – 2) = 0 so y = 0 or y = 2
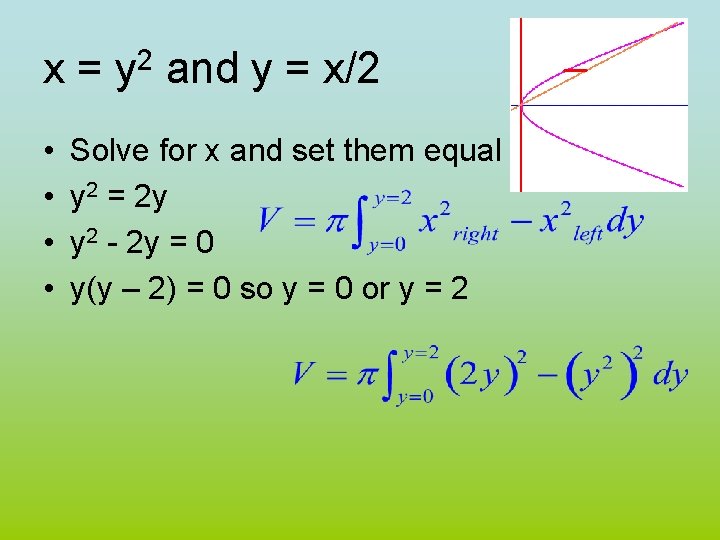
x = y 2 and y = x/2 • • Solve for x and set them equal y 2 = 2 y y 2 - 2 y = 0 y(y – 2) = 0 so y = 0 or y = 2

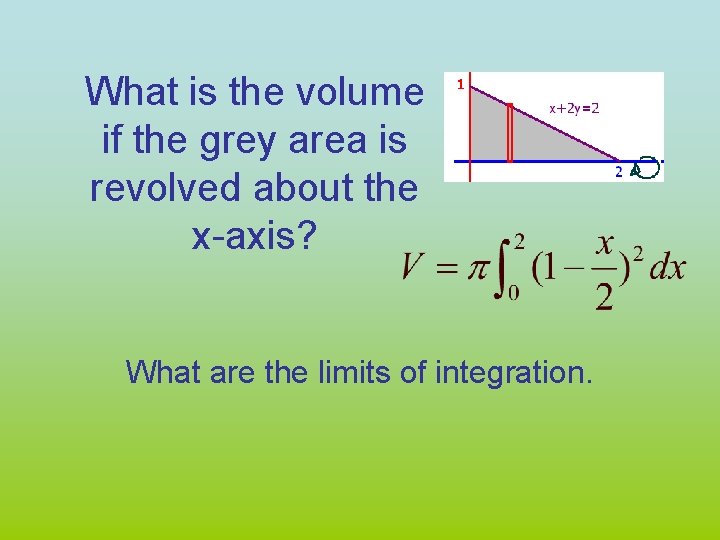
What is the volume if the grey area is revolved about the x-axis? What are the limits of integration.
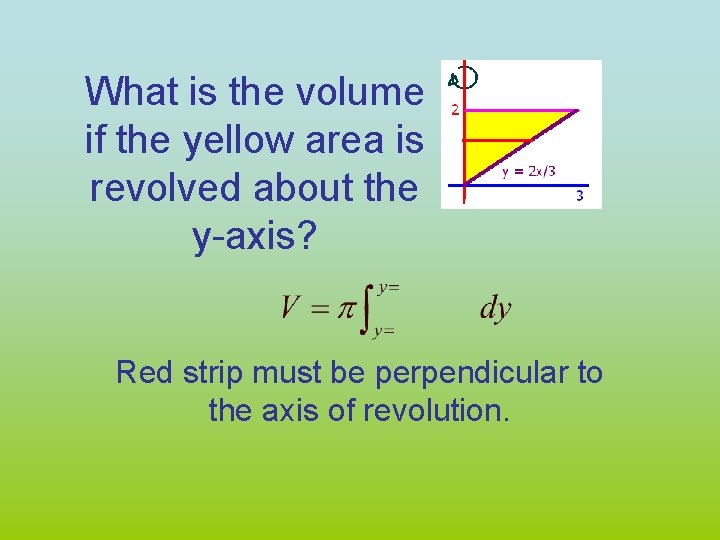
What is the volume if the yellow area is revolved about the y-axis? Red strip must be perpendicular to the axis of revolution.
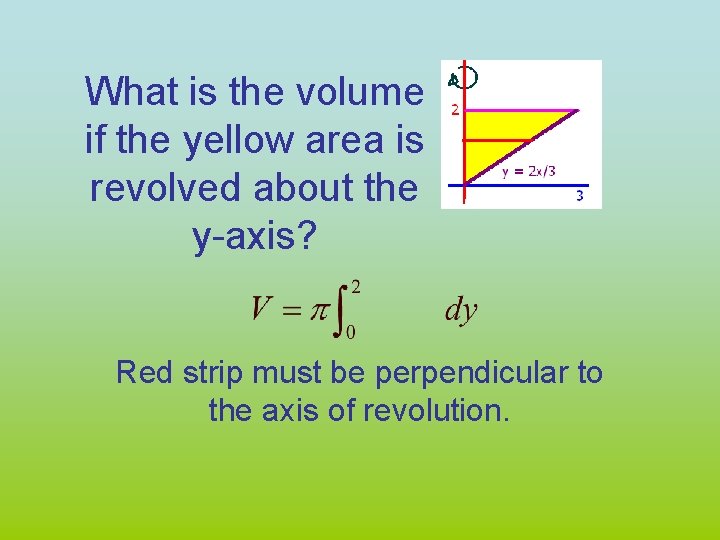
What is the volume if the yellow area is revolved about the y-axis? Red strip must be perpendicular to the axis of revolution.

What is the volume if the yellow area is revolved about the y-axis? Red strip must be perpendicular to the axis of revolution.
![p30 1 =-p/3[0 -1]](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-47.jpg)
=-p/3[0 -1]




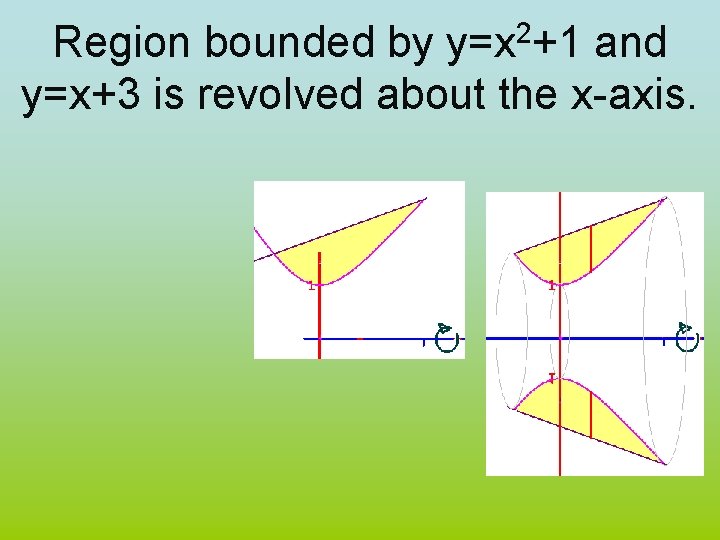
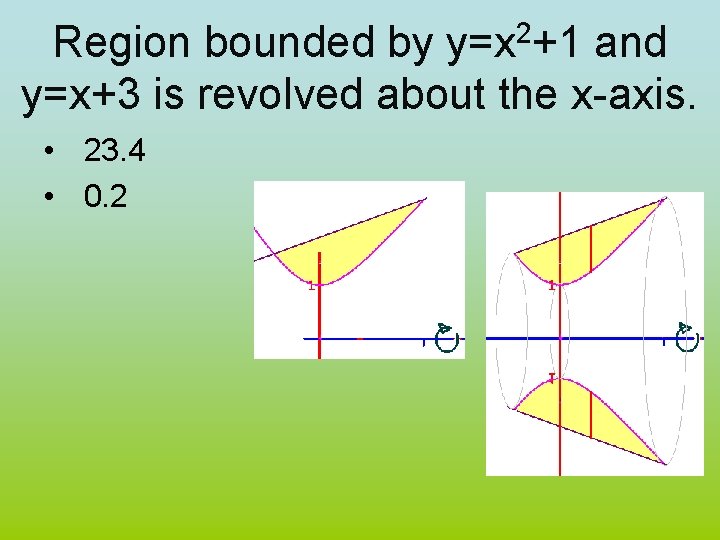
2 y=x +1 Region bounded by and y=x+3 is revolved about the x-axis.

2 y=x +1 Region bounded by and y=x+3 is revolved about the x-axis. • 23. 4 • 0. 2
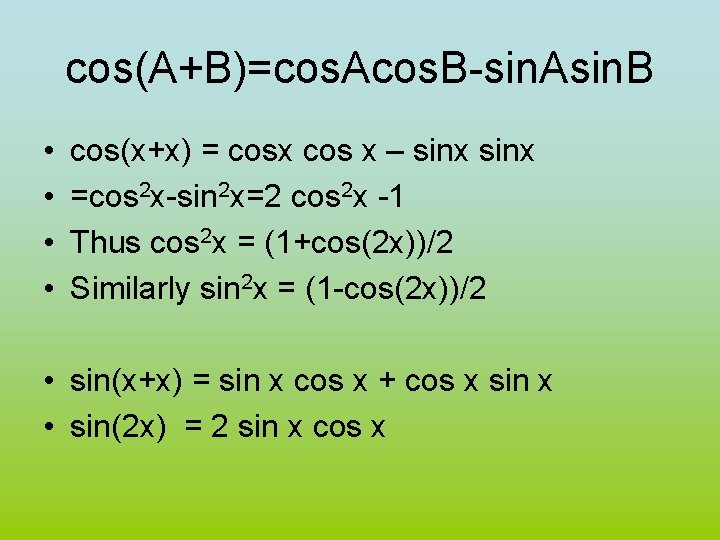
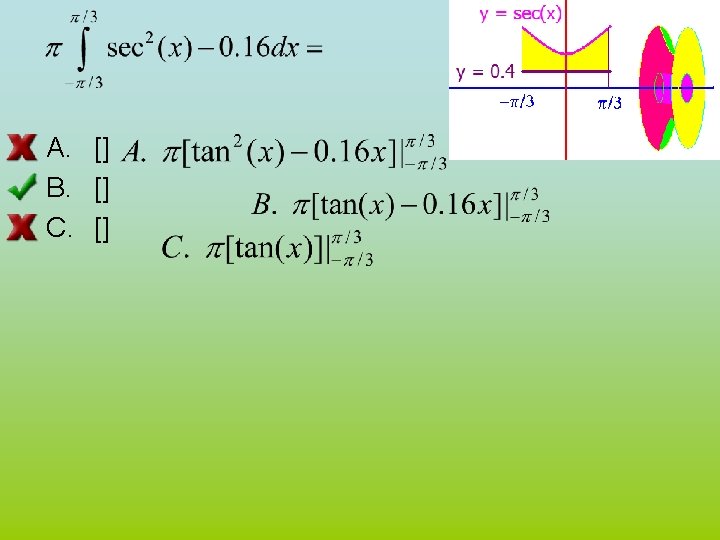
cos(A+B)=cos. Acos. B-sin. Asin. B • • cos(x+x) = cosx cos x – sinx =cos 2 x-sin 2 x=2 cos 2 x -1 Thus cos 2 x = (1+cos(2 x))/2 Similarly sin 2 x = (1 -cos(2 x))/2 • sin(x+x) = sin x cos x + cos x sin x • sin(2 x) = 2 sin x cos x
![A B C First two places ycosx and y2 sinxcosx cross x p3 A. B. C. First two places y=cosx and y=2 sinxcosx cross? ] x= p/3,](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-54.jpg)
A. B. C. First two places y=cosx and y=2 sinxcosx cross? ] x= p/3, p x=p/3, p/2 x=p/6, p/2

What is the area between them? A. B. C. .

![0 25 0 1 ] 0. 25 0. 1](https://slidetodoc.com/presentation_image_h/159cfd9c2f48520458e14a532f729d94/image-57.jpg)
] 0. 25 0. 1