Rhombi and Squares Lesson 6 4 Rhombus Square

Rhombi and Squares Lesson 6 -4: Rhombus & Square 1
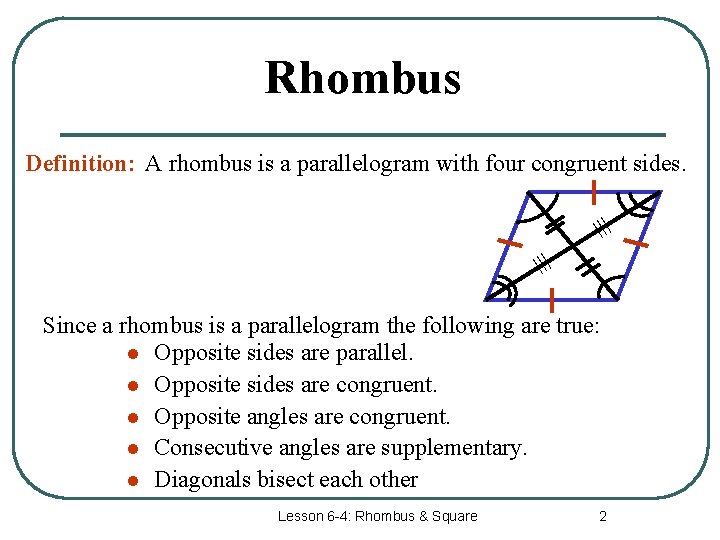
Rhombus Definition: A rhombus is a parallelogram with four congruent sides. ≡ ≡ Since a rhombus is a parallelogram the following are true: l Opposite sides are parallel. l Opposite sides are congruent. l Opposite angles are congruent. l Consecutive angles are supplementary. l Diagonals bisect each other Lesson 6 -4: Rhombus & Square 2
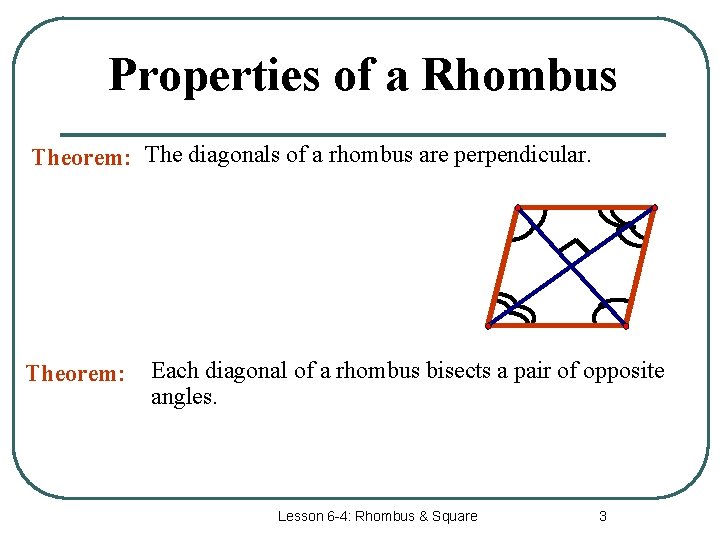
Properties of a Rhombus Theorem: The diagonals of a rhombus are perpendicular. Theorem: Each diagonal of a rhombus bisects a pair of opposite angles. Lesson 6 -4: Rhombus & Square 3
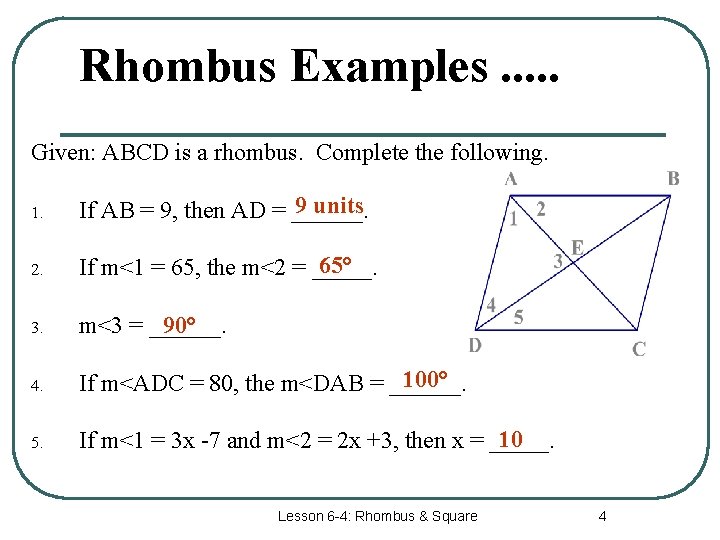
Rhombus Examples. . . Given: ABCD is a rhombus. Complete the following. 1. 9 units If AB = 9, then AD = ______. 2. 65° If m<1 = 65, the m<2 = _____. 3. 90° m<3 = ______. 4. 100° If m<ADC = 80, the m<DAB = ______. 5. 10 If m<1 = 3 x -7 and m<2 = 2 x +3, then x = _____. Lesson 6 -4: Rhombus & Square 4

Square Definition: A square is a parallelogram with four congruent angles and four congruent sides. Since every square is a parallelogram as well as a rhombus and rectangle, it has all the properties of these quadrilaterals. l l l l Opposite sides are parallel. Four right angles. Four congruent sides. Consecutive angles are supplementary. Diagonals are congruent. Diagonals bisect each other. Diagonals are perpendicular. Each diagonal bisects a pair of opposite angles. Lesson 6 -4: Rhombus & Square 5
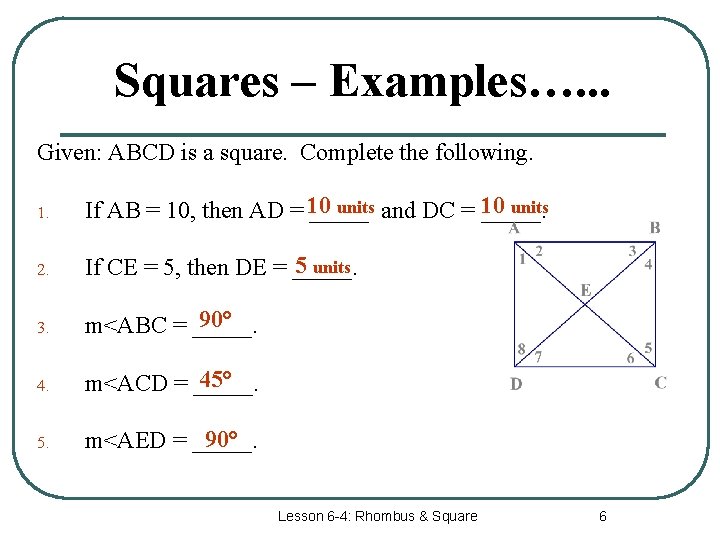
Squares – Examples…. . . Given: ABCD is a square. Complete the following. 1. units and DC = _____. 10 units If AB = 10, then AD = 10 _____ 2. 5 units If CE = 5, then DE = _____. 3. 90° m<ABC = _____. 45° m<ACD = _____. 5. 90° m<AED = _____. Lesson 6 -4: Rhombus & Square 6

Lesson 6 -3 Rectangles Lesson 6 -3: Rectangles 7

Rectangles Definition: A rectangle is a parallelogram with four right angles. A rectangle is a special type of parallelogram. Thus a rectangle has all the properties of a parallelogram. l l l Opposite sides are parallel. Opposite sides are congruent. Opposite angles are congruent. Consecutive angles are supplementary. Diagonals bisect each other. Lesson 6 -3: Rectangles 8

Properties of Rectangles Theorem: If a parallelogram is a rectangle, then its diagonals are congruent. Therefore, ∆AEB, ∆BEC, ∆CED, and ∆AED are isosceles triangles. A B E D C Converse: If the diagonals of a parallelogram are congruent , then the parallelogram is a rectangle. Lesson 6 -3: Rectangles 9

Examples……. 1. If AE = 3 x +2 and BE = 29, find the value of x. x = 9 units 10. 5 units 2. If AC = 21, then BE = _______. 3. If m<1 = 4 x and m<4 = 2 x, find the value of x. x = 18 units 4. If m<2 = 40, find m<1, m<3, m<4, m<5 and m<6. A m<1=50, m<3=40, m<4=80, m<5=100, m<6=40 B 1 2 3 4 D E 5 6 Lesson 6 -3: Rectangles C 10
- Slides: 10