REZOLVAREA UNOR PROBLEME CU AJUTORUL PRINCIPIILOR MECANICII CLASICE

REZOLVAREA UNOR PROBLEME CU AJUTORUL PRINCIPIILOR MECANICII CLASICE 1

Problema 1 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan înclinat de unghi , cunoscând coeficientul de frecare la alunecare . Aplicaţie numerică: = 300, = /4 2

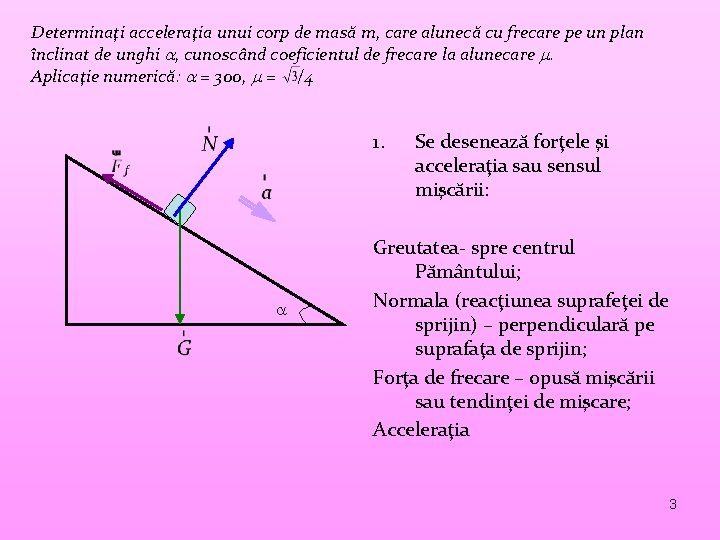
Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan înclinat de unghi , cunoscând coeficientul de frecare la alunecare . Aplicaţie numerică: = 300, = /4 1. Se desenează forţele şi acceleraţia sau sensul mişcării: Greutatea- spre centrul Pământului; Normala (reacţiunea suprafeţei de sprijin) – perpendiculară pe suprafaţa de sprijin; Forţa de frecare – opusă mişcării sau tendinţei de mişcare; Acceleraţia 3

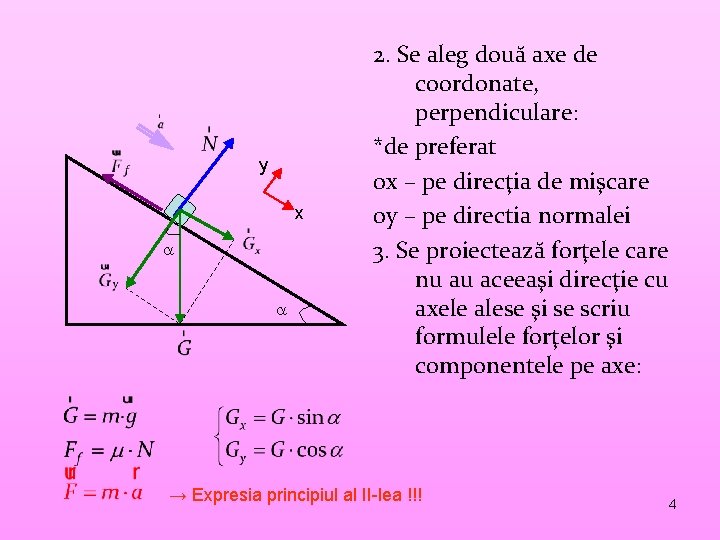
y x 2. Se aleg două axe de coordonate, perpendiculare: *de preferat 0 x – pe direcţia de mişcare 0 y – pe directia normalei 3. Se proiectează forţele care nu au aceeaşi direcţie cu axele alese şi se scriu formulele forţelor şi componentele pe axe: → Expresia principiul al II-lea !!! 4

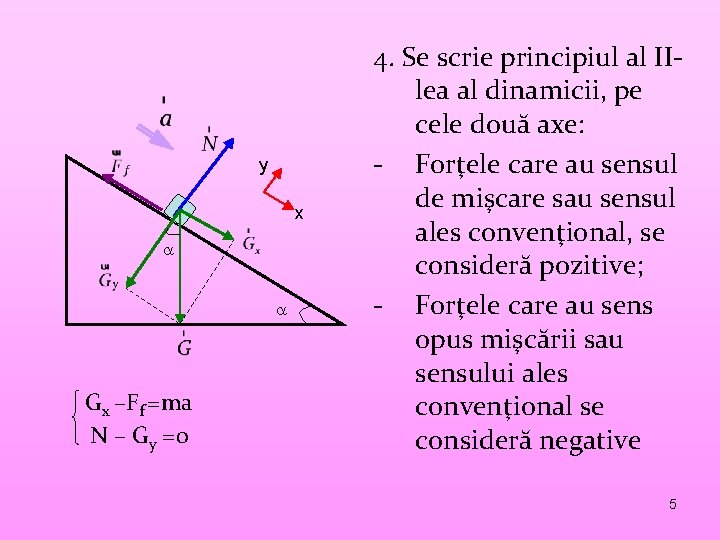
y x Gx –Ff =ma N – Gy =0 4. Se scrie principiul al IIlea al dinamicii, pe cele două axe: - Forţele care au sensul de mişcare sau sensul ales convenţional, se consideră pozitive; - Forţele care au sens opus mişcării sau sensului ales convenţional se consideră negative 5

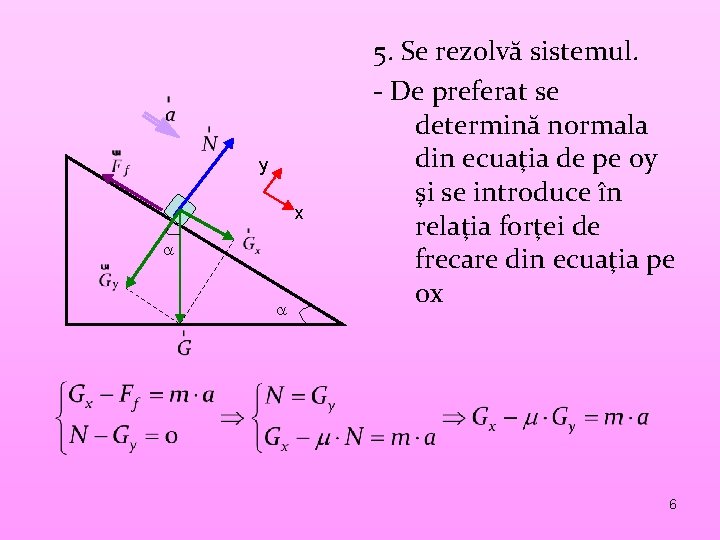
y x 5. Se rezolvă sistemul. - De preferat se determină normala din ecuaţia de pe oy şi se introduce în relaţia forţei de frecare din ecuaţia pe ox 6

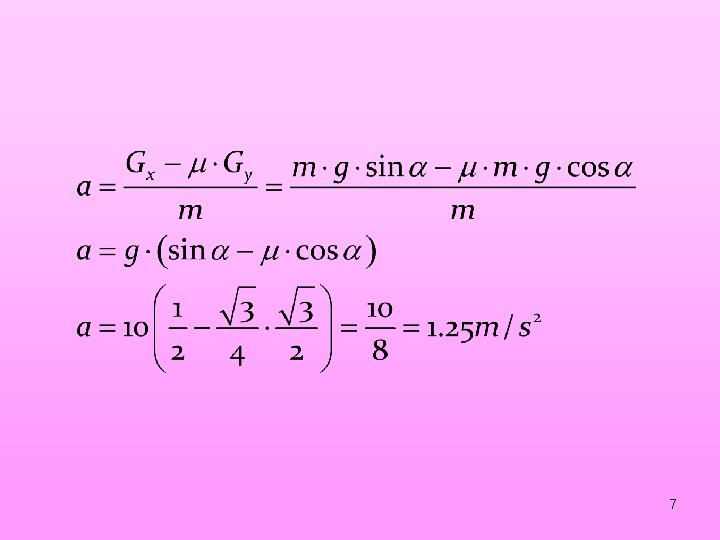
7

Problema 2 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare . 8

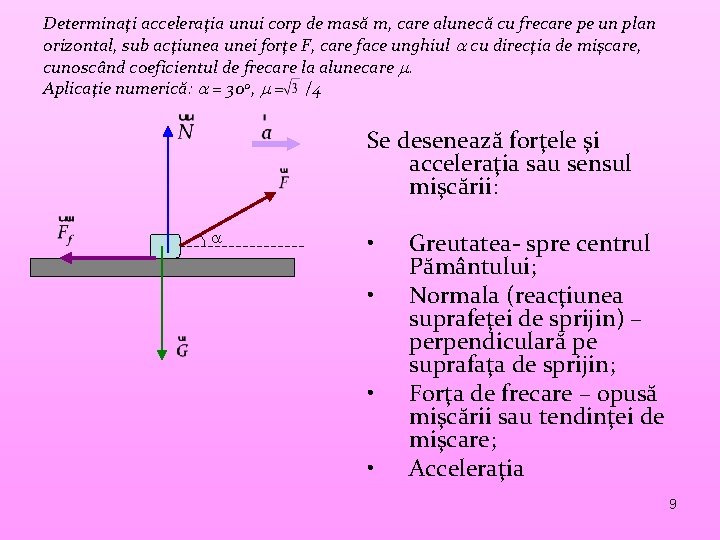
Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare . Aplicaţie numerică: = 300, = /4 Se desenează forţele şi acceleraţia sau sensul mişcării: • • Greutatea- spre centrul Pământului; Normala (reacţiunea suprafeţei de sprijin) – perpendiculară pe suprafaţa de sprijin; Forţa de frecare – opusă mişcării sau tendinţei de mişcare; Acceleraţia 9

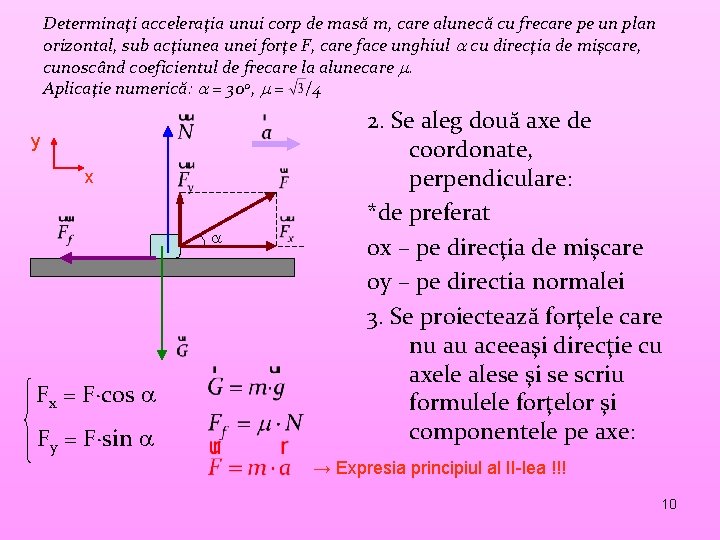
Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare . Aplicaţie numerică: = 300, = /4 y x Fx = F∙cos Fy = F∙sin 2. Se aleg două axe de coordonate, perpendiculare: *de preferat 0 x – pe direcţia de mişcare 0 y – pe directia normalei 3. Se proiectează forţele care nu au aceeaşi direcţie cu axele alese şi se scriu formulele forţelor şi componentele pe axe: → Expresia principiul al II-lea !!! 10

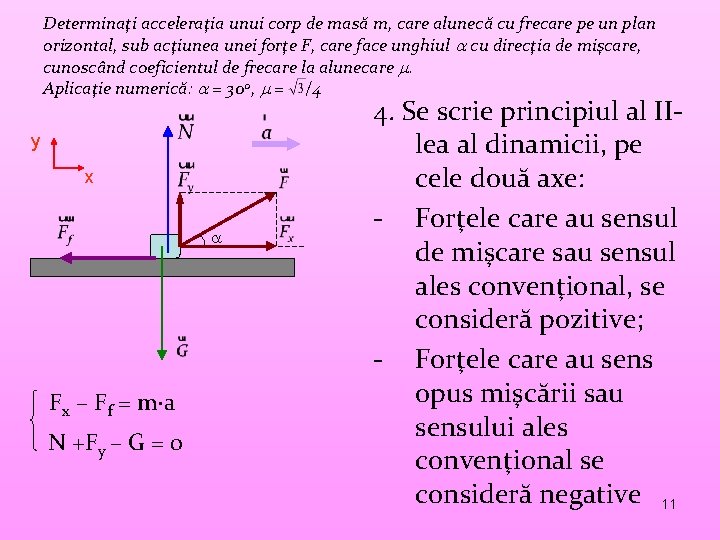
Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare . Aplicaţie numerică: = 300, = /4 y x Fx – Ff = m a N +Fy – G = 0 4. Se scrie principiul al IIlea al dinamicii, pe cele două axe: - Forţele care au sensul de mişcare sau sensul ales convenţional, se consideră pozitive; - Forţele care au sens opus mişcării sau sensului ales convenţional se consideră negative 11

Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare . Aplicaţie numerică: = 300, = /4 5. Se rezolvă sistemul. - De preferat se determină normala din ecuaţia de pe oy şi se introduce în relaţia forţei de frecare din ecuaţia pe ox y x Fx – Ff = m a N +Fy – G = 0 N = G - Fy Fx – ∙N = m a Fx – ∙ (G – Fy) = m a a = [Fx – ∙ (G – Fy)]/m 12

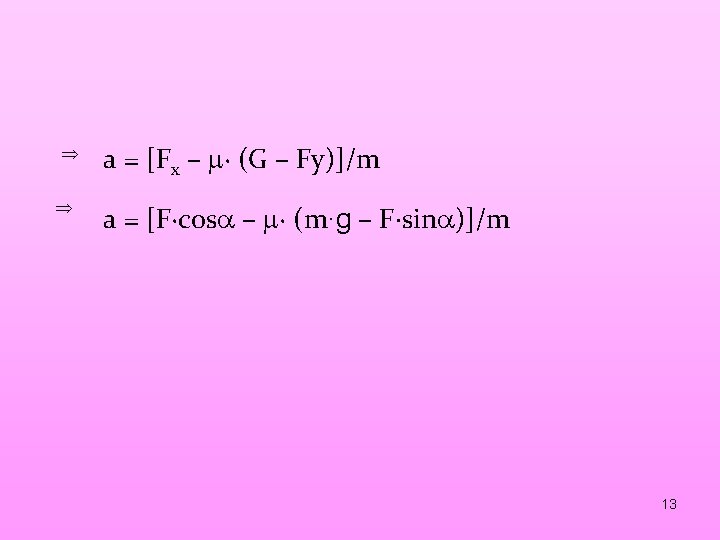
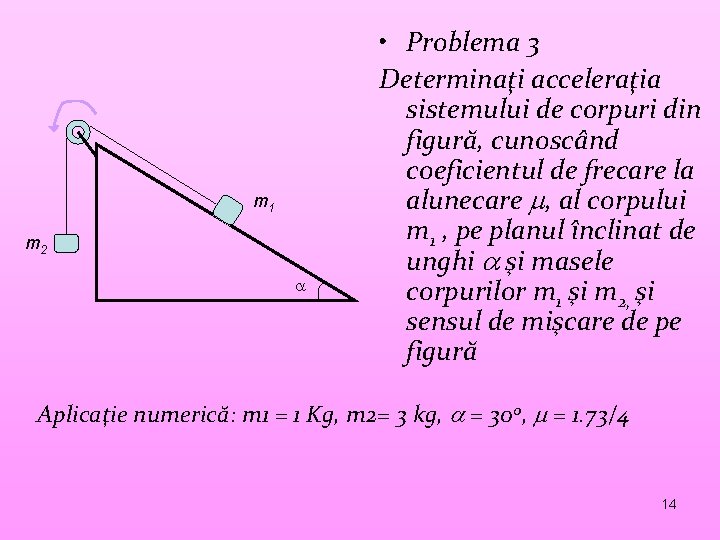
m 1 m 2 • Problema 3 Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare , al corpului m 1 , pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură Aplicaţie numerică: m 1 = 1 Kg, m 2= 3 kg, = 300, = 1. 73/4 14

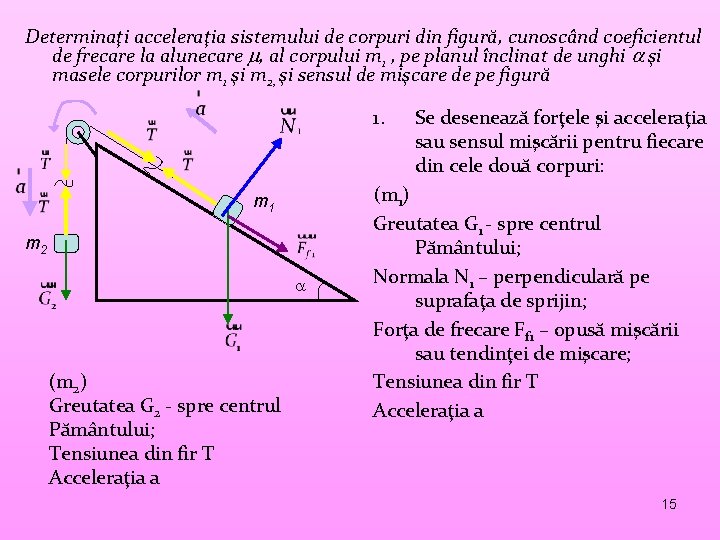
Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare , al corpului m 1 , pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură 1. m 1 m 2 (m 2) Greutatea G 2 - spre centrul Pământului; Tensiunea din fir T Acceleraţia a Se desenează forţele şi acceleraţia sau sensul mişcării pentru fiecare din cele două corpuri: (m 1) Greutatea G 1 - spre centrul Pământului; Normala N 1 – perpendiculară pe suprafaţa de sprijin; Forţa de frecare Ff 1 – opusă mişcării sau tendinţei de mişcare; Tensiunea din fir T Acceleraţia a 15

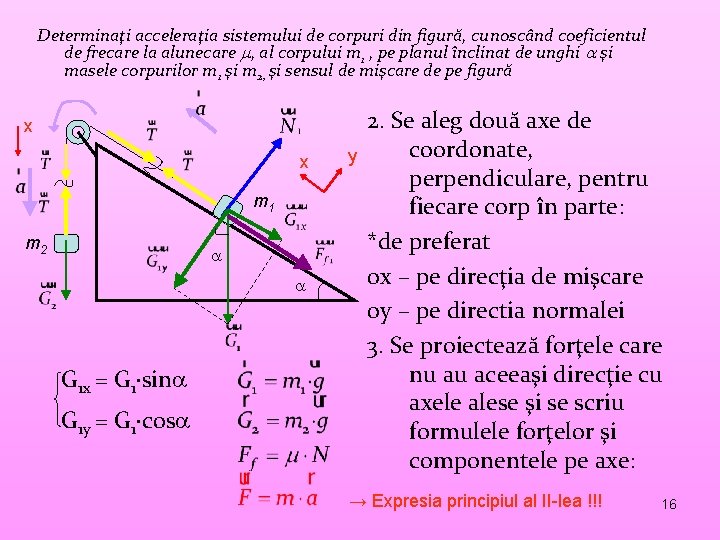
Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare , al corpului m 1 , pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură x x m 1 m 2 G 1 x = G 1 sin G 1 y = G 1 cos y 2. Se aleg două axe de coordonate, perpendiculare, pentru fiecare corp în parte: *de preferat 0 x – pe direcţia de mişcare 0 y – pe directia normalei 3. Se proiectează forţele care nu au aceeaşi direcţie cu axele alese şi se scriu formulele forţelor şi componentele pe axe: → Expresia principiul al II-lea !!! 16

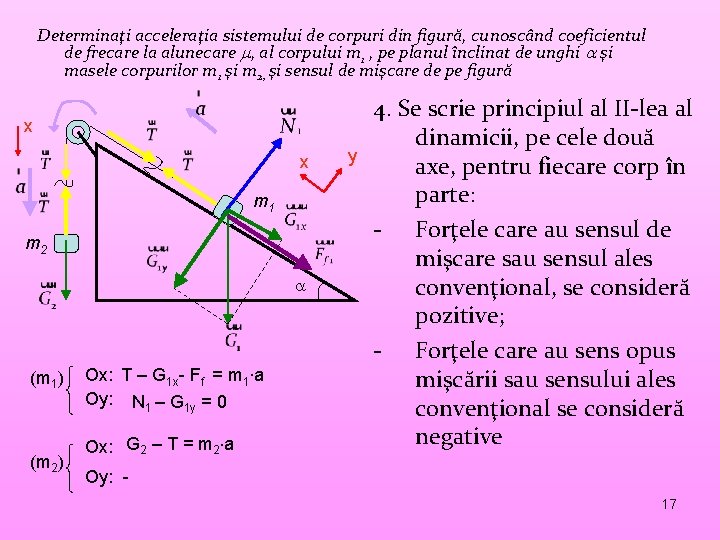
Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare , al corpului m 1 , pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură x x m 1 m 2 (m 1) (m 2) Ox: T – G 1 x- Ff = m 1∙a Oy: N 1 – G 1 y = 0 Ox: G 2 – T = m 2 a y 4. Se scrie principiul al II-lea al dinamicii, pe cele două axe, pentru fiecare corp în parte: - Forţele care au sensul de mişcare sau sensul ales convenţional, se consideră pozitive; - Forţele care au sens opus mişcării sau sensului ales convenţional se consideră negative Oy: 17

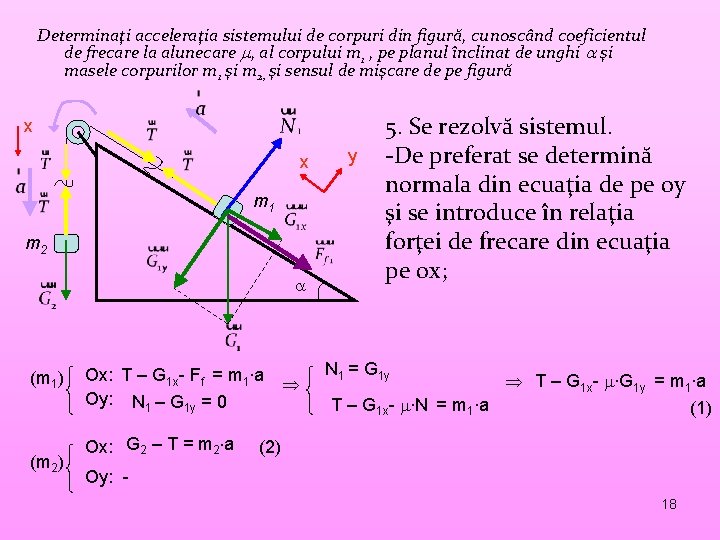
Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare , al corpului m 1 , pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură x x m 1 m 2 (m 1) (m 2) Ox: T – G 1 x- Ff = m 1∙a Oy: N 1 – G 1 y = 0 Ox: G 2 – T = m 2 a y 5. Se rezolvă sistemul. -De preferat se determină normala din ecuaţia de pe oy şi se introduce în relaţia forţei de frecare din ecuaţia pe ox; N 1 = G 1 y T – G 1 x- ∙G 1 y = m 1∙a T – G 1 x- ∙N = m 1∙a (1) (2) Oy: 18

• Cu relaţiile (1) şi (2) se formează un sistem din care se determină necunoscutele, în acest caz: a şi T T – G 1 x- ∙G 1 y = m 1∙a G 2 – T = m 2 a (+) G 2 - G 1 x- ∙G 1 y = ( m 1+ m 2 )∙a a = (G 2 - G 1 x- ∙G 1 y )/( m 1+ m 2 ) a = (m 2 g - m 1∙g sin - ∙m 1 g∙cos )/( m 1+ m 2 ) Calcul numeric : D 19